常见损失函数Loss Function的选择(regression problem)

news2024/9/20 0:57:20

损失函数Loss Function的设计是机器学习模型的核心问题，一般情况下函数式子会分成两项：衡量预估值和目标间的差距 $L(y_i, f_{\theta}(x_i))$ 、正则项式 $R(\theta )$ 。其中正则项式子一般用于衡量模型的复杂度，可以避免模型过拟合（奥卡姆剃刀原理）。

$\min\sum L(y_i, f_{\theta}(x_i)) + \lambda R(\theta )$

另一部分衡量预估值和目标间差距的函数，是本文所重点介绍的，比如MSE损失函数用于预估值与目标值的均方误差，在实际情景中，这部分的损失函数可能包含从多种方面反映预估同目标差距的组合，比如存在多个目标的情况。另一种情况是包含反映某些中间结构偏离的损失，但这种中间结果偏离一般不建议直接引入损失函数中，多数学者认为损失函数应只包含预测同目标直接相关的损失，中间结果的偏离损失（从先验知识中得到的）应该通过正则项引入。

本文将主要介绍回归类问题的常见损失函数，在实际工业场景中，很难直接认为某种损失函数更好，而是结合自身模型和目标的实际，去设计合适的损失函数（不一定是如下的几种）能精确衡量预测同目标的差距，更重要的是能帮忙模型去正确学习。

1. MSE损失函数

MSE损失函数又被称为平方损失square loss，或者L2损失，其定义为：

$L_{MSE}(y_i,f_{\theta }(x_i))=(y_i - f_{\theta }(x_i))^2$

当在mini-batch中，计算batch的损失时，一般有两种方式（mean或sum），下式中n表示mini-batch的size。

$L=\left\{\begin{matrix} \frac{1}{n}\sum_i^nL_{MSE}(y_i, f_{\theta }(x_i))\\ \sum_i^nL_{MSE}(y_i, f_{\theta }(x_i)) \end{matrix}\right.$

2. MAE损失函数

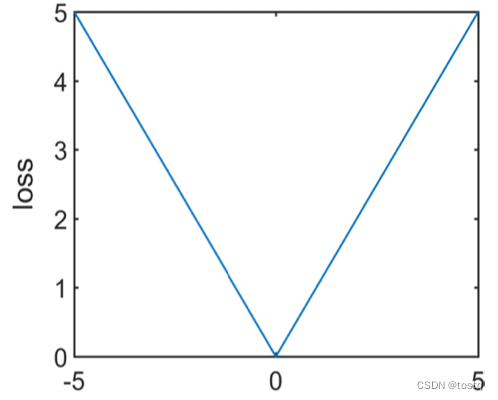
MAE损失函数又被称为绝对损失absolute loss，或者L1损失，其定义为：

$L_{MAE}(y_i,f_{\theta }(x_i))=|y_i - f_{\theta }(x_i)|$

当在mini-batch中，计算batch的总损失时，同MSE一样，也有两种方式（mean或sum）。MSE相比于MAE来说，当 $y_i - f_{\theta }(x_i)$ 间差别较大时，MSE的loss远比MAE大，因此MSE相较于MAE对于离群点的损失更为敏感。

从另一方面上看，MSE更倾向于预估样本均值，而MAE更倾向于预估样本中位数，我们简单从梯度上分析下，首先对于MSE来说，当其权重梯度为0时模型将会收敛，此时如果当 $f_{\theta }(x_i)$ 恰好等于 $y_i$ 均值时，下式的权重梯度是为0的。

$\frac{\partial L_{MSE}}{\partial \theta }=\sum_i^n-2(y_i-f_{\theta }(x_i))\frac{\partial f_{\theta }(x_i)}{\partial \theta }$

而对于MAE来说，此时当 $f_{\theta }(x_i)$ 恰好等于 $y_i$ 中位数时，下式的权重梯度是为0的。

$\frac{\partial L_{MAE}}{\partial \theta }=\sum_i^n \mathbb{I} \frac{\partial f_{\theta }(x_i)}{\partial \theta },\ \left\{\begin{matrix} \mathbb{I}=1\ \text{if}\ y_i < f_{\theta }(x_i)\\ \mathbb{I}=-1\ \text{if}\ y_i > f_{\theta }(x_i)\\ \mathbb{I}=0\ \text{if}\ y_i = f_{\theta }(x_i) \end{matrix}\right.$

3. huber损失函数

huber损失函数是L1损失和L2损失函数一种结合，其定义为：

$L_{huber}(y_i, f_{\theta }(x_i))=\left\{\begin{matrix} \frac{1}{2}(y_i - f_{\theta }(x_i))^2 \ \text{if } |y_i - f_{\theta }(x_i)|\leq \delta \\ \delta |y_i - f_{\theta }(x_i)|-\frac{1}{2}\delta^2 \ \text{if } |y_i - f_{\theta }(x_i)| > \delta \end{matrix}\right.$

huber损失函数结合了L1损失和L2损失函数的特性，在偏差较大范围应用L1损失函数，减少了离群点的损失权重，而偏差较小范围就用L2损失函数，当 $\delta \leq 1$ 时，L2的损失梯度要小于L1的损失梯度，因此对于小偏差更灵敏，更容易找到局部最优，而当 $\delta > 1\ \&\&\ 1<|y_i-f_{\theta }(x_i)|<\delta$ 时，L2的损失梯度要比L1的损失梯度要更大，因此在一定范围内的离群点的损失更为敏感。在实际应用时， $\delta$ 不仅可以做为一个超参数，甚至可以作为一个学习参数。

4. Log-cosh损失函数

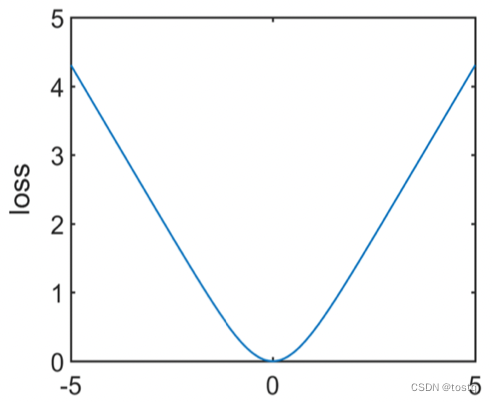
log-cosh损失函数也是类似于huber损失函数一类变种损失函数，其定义为：

$L_{logcosh}(y_i,f_{\theta }(x_i))=log(cosh(y_i-f_{\theta }(x_i))),\ cosh(x)=\frac{e^x+e^{-x}}{2}$

log-cosh损失函数在偏差较小时类似于MSE，在偏差较大值类似于MAE，这个同huber损失是类似的，但log-cosh是处处存在二阶可导，在一些需要用到二阶导数的机器学习算法（XGBoost）比如中更为适合。

5. Quantile损失函数

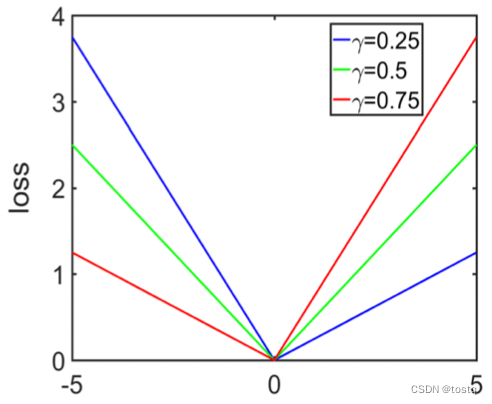
Quantile损失函数又被称为分位数损失函数，是MAE函数一类变种损失函数，其定义如下：

$L_{Quantile}(y_i,f_{\theta }(x_i))=\left\{\begin{matrix} (1-\gamma )|y_i-f_{\theta }(x_i)|\text{ if } y_i \leq f_{\theta }(x_i)\\ \gamma|y_i-f_{\theta }(x_i)|\text{ if } y_i > f_{\theta }(x_i) \end{matrix}\right.$

上文指出MAE函数实际上会倾向于预估样本中位数，我们可以很容易推导出Quantile系列损失函数会倾向于预估样本分位数。因此在某些区间预估的场景，Quantile系列损失函数会非常有用。

6. 𝜖-insensitive损失函数

𝜖-insensitive损失函数主要是为了避免MAE损失函数在偏差较小时太过敏感，从而导致训练振荡，其定义为：

$L_{\varepsilon MAE}(y_i,f_{\theta }(x_i))=\left\{\begin{matrix} |y_i-f_{\theta }(x_i)|-\varepsilon \text{ if } |y_i-f_{\theta }(x_i)| \geq \varepsilon \\ 0 \text{ if } |y_i-f_{\theta }(x_i)| < 0 \end{matrix}\right.$

7. 更为通用的回归损失函数

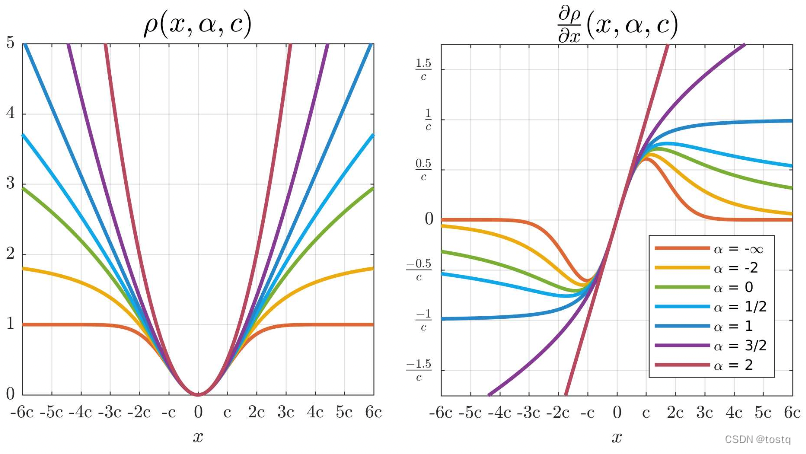
google提出了更为通用性的回归损失函数，其定义为：

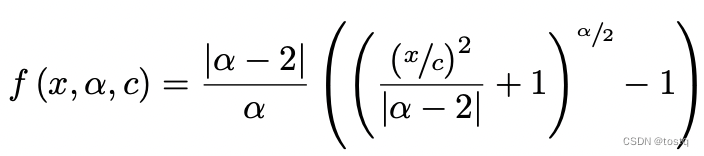
上式中x表示预估和目标的偏差 $y_i-f_{\theta }(x_i)$ ， $\alpha,\ c$ 是可训练的超参数，其中 $\alpha$ 参数可以调整损失函数的形状，当 $\alpha =1$ 时，近似于平滑的L1损失函数，而当 $\alpha =2$ 时，近似于L2损失函数。当 $\alpha$ 越小时，对于离群点越不敏感，当 $\alpha=-\infty$ 时，此时当偏差大于3c时其梯度为0，倾向于寻找局部最优点。超参数 $\alpha,\ c$ 可以做为固定超参数，或者做可作为自适应调整的学习参数。

总结

上述是常用的回归问题的损失函数，其在设计上不同主要是考虑对离群点的处理（比如L1损失函数主要考虑是中位数损失，而L2损失函数考虑的整体平均损失）。但在实际中，回归类问题远比分类问题要难。

首先当数据分布上偏差，因为上述损失函数是建立在数据分布均匀的情况下，所以当某一区间值覆盖特别多情况下，直接应用上述损失函数，会使得预估值往高比例区间偏移。一种解决方法是使用加权损失函数（Focal Loss 和 Dice Loss），其中每个类别的损失函数权重与其在数据集中的比例成反比。这意味着，对于数量较少的类别，其损失函数的权重会更大，从而强制模型更加关注这些类别，从而提高模型对这些类别的预测准确率。另一种解决方法是使用数据增强技术，例如对少数类别的样本进行过采样或者对多数类别的样本进行欠采样，从而使得各个类别的样本数量更加均衡。但这两种方式虽然能加强对数量较少类别的训练，但不可避免也会给整体带来新偏差，因此可以在应用加权训练，再重新用未加权的数据进行训练，避免数据偏差的引入。

其次，数据本身值会可能会给Loss计算带来偏差，比如某些大值计算的loss会偏大，同时大值本身在计算梯度时可能会陷入不激活区域，影响整体模型的收敛。这种情况下，可以通过归一化等方向去解决，但如果进行合适的归一化需要仔细的设计。

另外，回归类问题数据稀疏性远比分类问题要大，或者说回归类问题的寻值空间很大，因此模型学习可能要花更长时间进行收敛，同时参数量和模型结构都要比分类问题复杂。所以另外一些成熟的做法是将回归类问题转换为分类问题来解决，一种常见的方法是将连续输出变量转换为离散的类别（即分桶方法），另外youtube的weightLR对时长预估是另一类非常巧妙的方法。