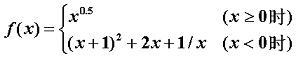DAC 2021
背景
通过ANN2SNN的方法得到的SNN中,存在准确性和延迟之间的一种权衡关系,在较大的数据集(如ImageNet)上可能会有较高的延迟。
主要贡献
- 分析了转换后SNN精度与延迟之间存在权衡关系的原因,并指出了如何缓解这种权衡关系;
- 提出TCL(trainable clipping layer)技术改善权衡关系,TCL的剪裁区域是被训练过的,跟着ReLU层,可以找到精度与延迟之间的最优数据归一化因子;
- 通过适当控制L2正则化系数,进一步提高了极低延迟约束下SNN的精度。
主要内容与方法
ANN2SNN误差分析
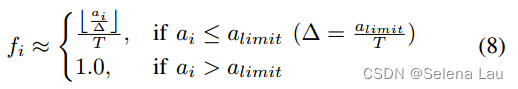
f是放电率,a是激活值,deta是量化解(我的理解是a_limit是转换中可映射的最大激活值)。
ANN2SNN实际上就是用量化的激活值匹配放电率,但量化误差是不可避免的。可以通过增加延迟T或者减小a_limit来减小量化误差,这也是ANN2SNN过程中存在精度和延迟之间权衡关系的原因。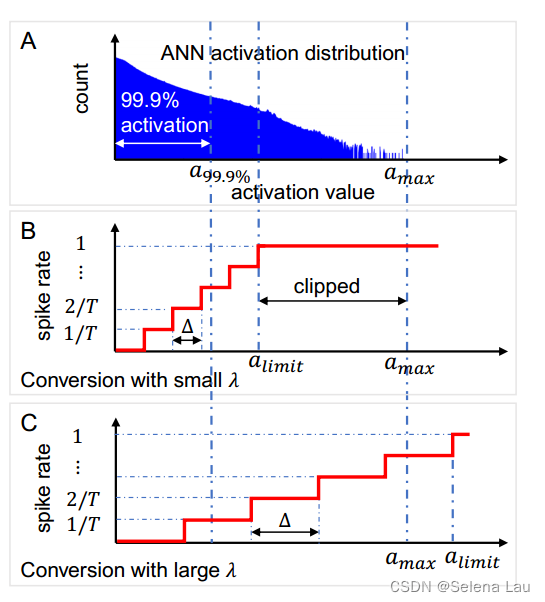
通过上面这个图也可以看到,ANN大部分激活值都不是特别接近最大激活值,有90.00%~99.99%都是在[0, max / 3]的范围里,但由于a_limit的选择,可能造成不同的损失:当a_limit<a_max,一部分激活值被剪裁掉了,造成了损失;当a_limit>a_max,又会造成量化误差。
可训练的剪裁层(Trainable Clipping Layer)
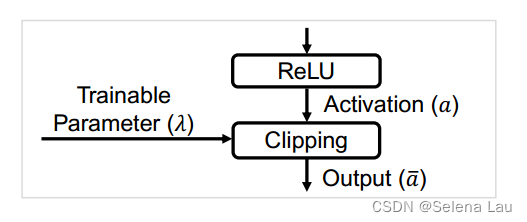
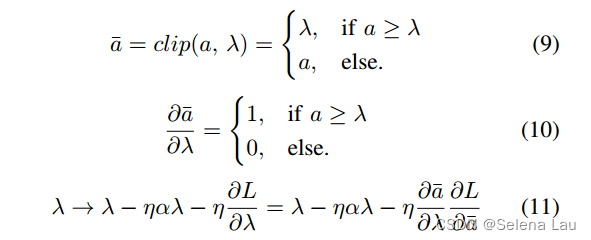
clipping layer的功能如(9)所示,λ是可训练参数,其梯度用(10)计算,更新规则如(11)。
其中η是学习率,α是L2正则化系数,L是ANN的loss。
实验结果
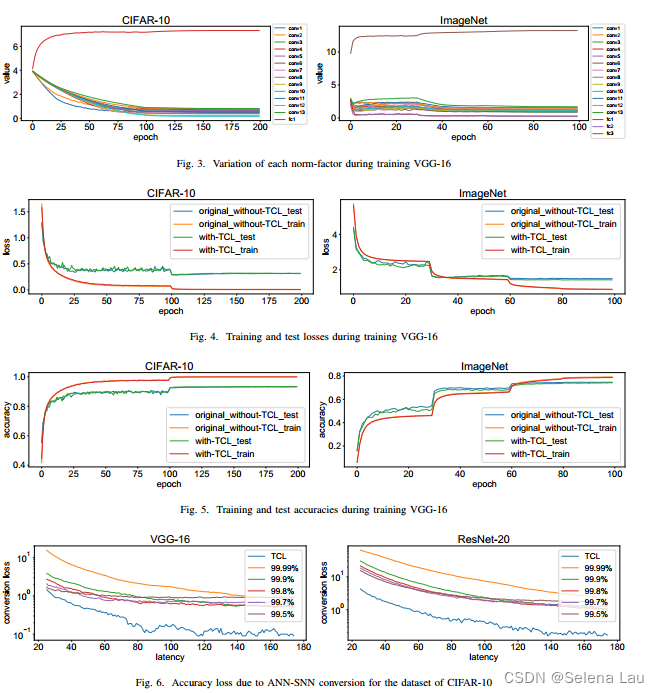
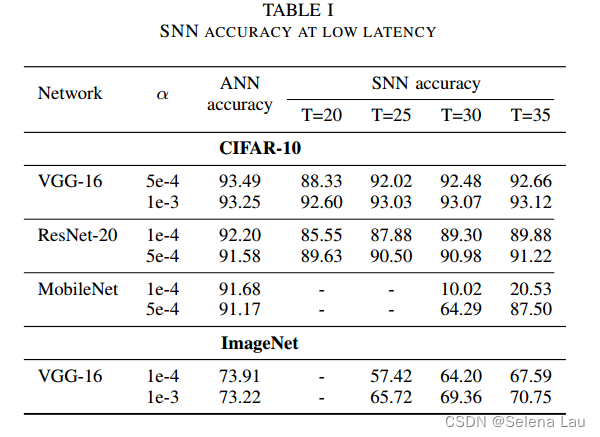
从实验结果可以看出,TCL技术对比SOTAs取得了两方面重要成就:
- 尽管限制了激活值的范围,TCL几乎不影响ANN的精度;
- 转换后的SNN具有与原ANN相当的精度,并且延迟也较为适中。
总结
本文提出了一种基于ANN-to-SNN转换的可训练剪裁层技术,即TCL,缓解了SNN精度和延迟之间的权衡关系。实验结果表明,基于TCL的SNN即使在250个时钟周期的小延迟下,也能获得几乎相当ANN的精度,很好地验证了TCL的有效性。