前言:15年Google提出Batch Normalization,成为深度学习最成功的设计之一,18年MIT团队将原论文中提出的BN层的作用进行了一一反驳,重新揭示BN层的意义
2015年Google团队论文:【here】
2018年MIT团队论文:【here】
How Does Batch Normalization Help Optimization?
原文观点
15年那篇论文里提出BN对网络起的作用是,减少了中间协变量偏移的影响 Internal Covariate Shift(ICS)。神经网络每一层在更新了权重之后的输出的分布是变化的,因此中间协变量也会有变化,通过将线性映射之后的输出“白化”,即控制均值为0,和方差恒为1,可以有效的将每一层网络学习的输入控制在一个相同的分布下,因此更有利于网络的学习。
反驳论点
这篇论文首先对原文引出的概念提出了两点质疑
第一,BN层的成功真的在于减少了中间协变量偏移吗?
Does BatchNorm’s performance stem from controlling internal covariate shift?
作者这里为了证明BN层的成功不在于减少了ICS,设计了三组参照实验,第一组不加BN,第二组加BN,第三组加了BN层之后又加上一个随机白噪声,有着不同的均值和方差,作者旨在通过第三组实验,模拟加了BN层但是ICS更高的场景
这三组实验在VGG的网络上的表现如下
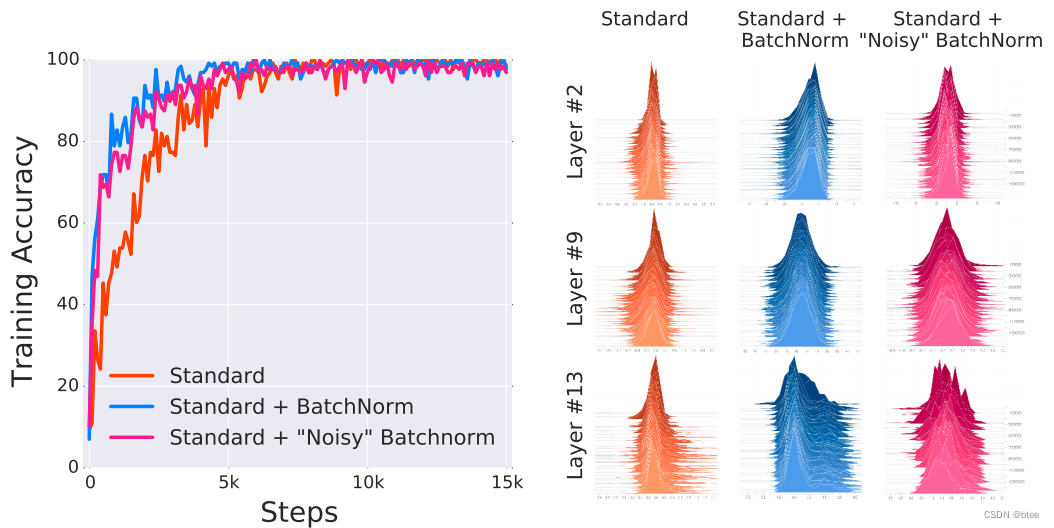
可以看到,加了BN层但是ICS更高的第三组实验比,标准实验(不加BN)取得更好的训练效果,中间变量均值偏移和方差偏移的可视化如下,可以看到:“噪声”网络比标准网络的ICS更高
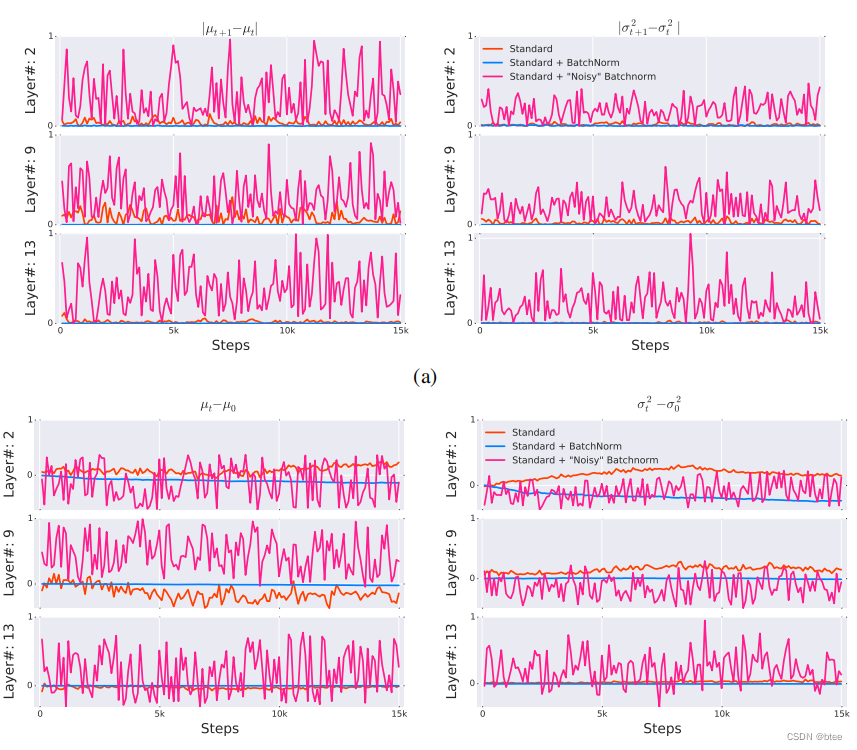
因此,这组实验可以证明,BN层可以帮助网络的训练,但并不在于ICS的减少,即不在于每一层的分布保持一致
作者紧接着提出了第二个质疑,即BN层的添加是否有减少ICS呢?即有没有一个更广泛的中间协变量偏移的概念(而不是均值方差的偏移),来证明与BN层网络的关系
第二,BatchNorm真的能减少ICS吗
Is BatchNorm reducing internal covariate shift?
本文作者认为,参数更新会导致这个损失函数最小化问题本身改变,这和原论文的作者直觉一致,但原论文作者从结果的分布来捕捉这样的现象,这没有触及到问题的本质。如果要挖掘这样的优化问题的本质,应该从优化参数的梯度去入手,因此提出了一种新的方式定义ICS,即用更新前和更新后的每一层参数的梯度的二范数来表示偏移。因此,梯度变化可以代表在每一次参数更新后,在这一层的损失图上的一个跨越
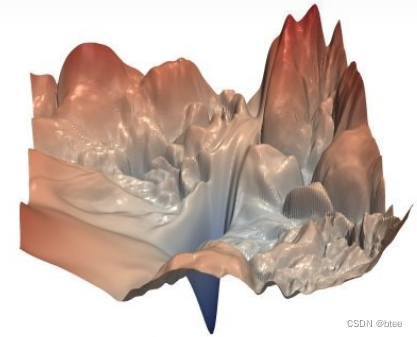
大概类似于这样的损失图上,如果ICS很大,在每一层的optimize landsacpe上的位置跨越就很大,导致梯度的变化很大

而结果也是令人震惊,加了BN层的ICS反而更大了,如下图右边
在学习率很大的时候,梯度的变化都是震荡得比较剧烈的,在学习率比较小的时候,不加BN的标准网络的梯度变化非常小(体现在接近1的余弦角度和很小的l2距离)
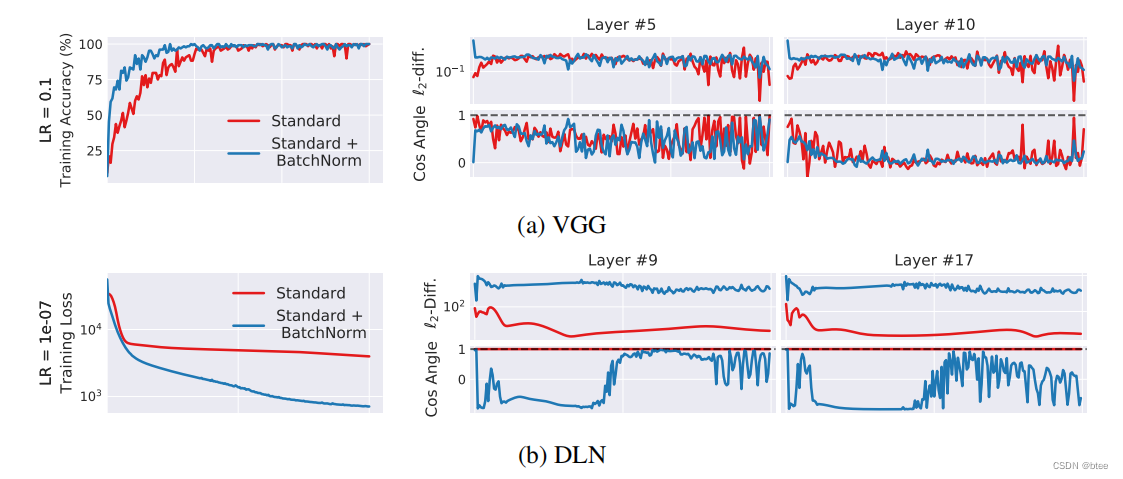
(这里我的理解是,由于不加BN的优化landscape不够光滑,如果梯度变化过大会导致掉到局部最优或者是进入平坦区域)BN使优化landscape变光滑了,每一次调整的梯度变大,因此也很快收敛
BN为什么工作
作者给出直接的观点,加了BN重新调整了网络的训练参数,使优化的landscape变得光滑
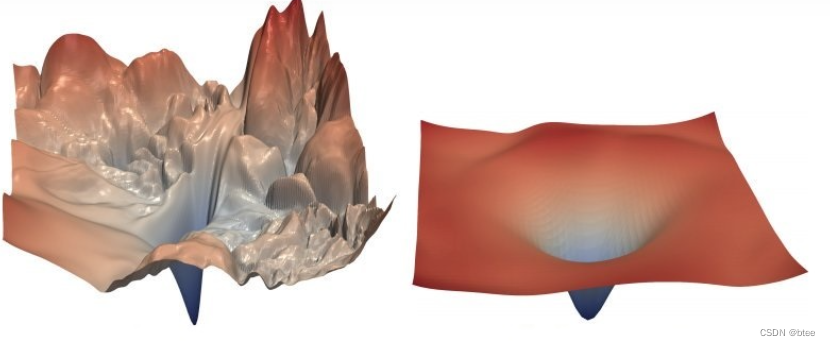
由于没法进行全局的landscape的可视化,作者通过几个参数来代表优化landscape的光滑程度
损失函数的变化
梯度的变化
β平滑度
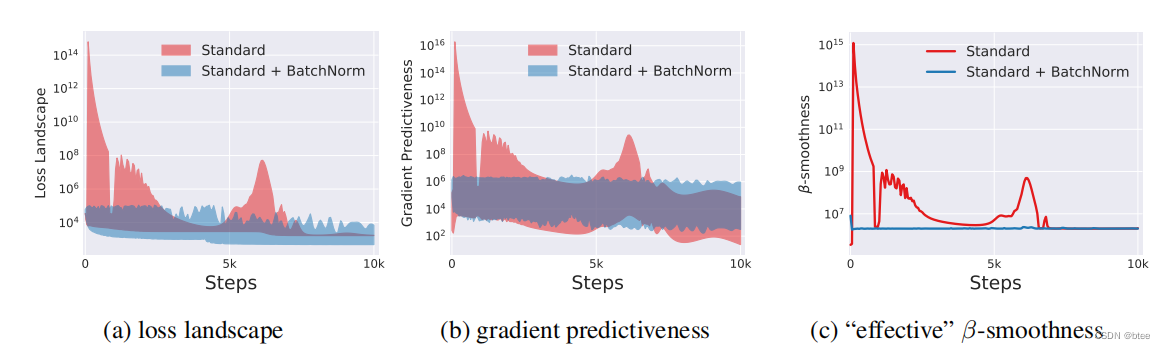
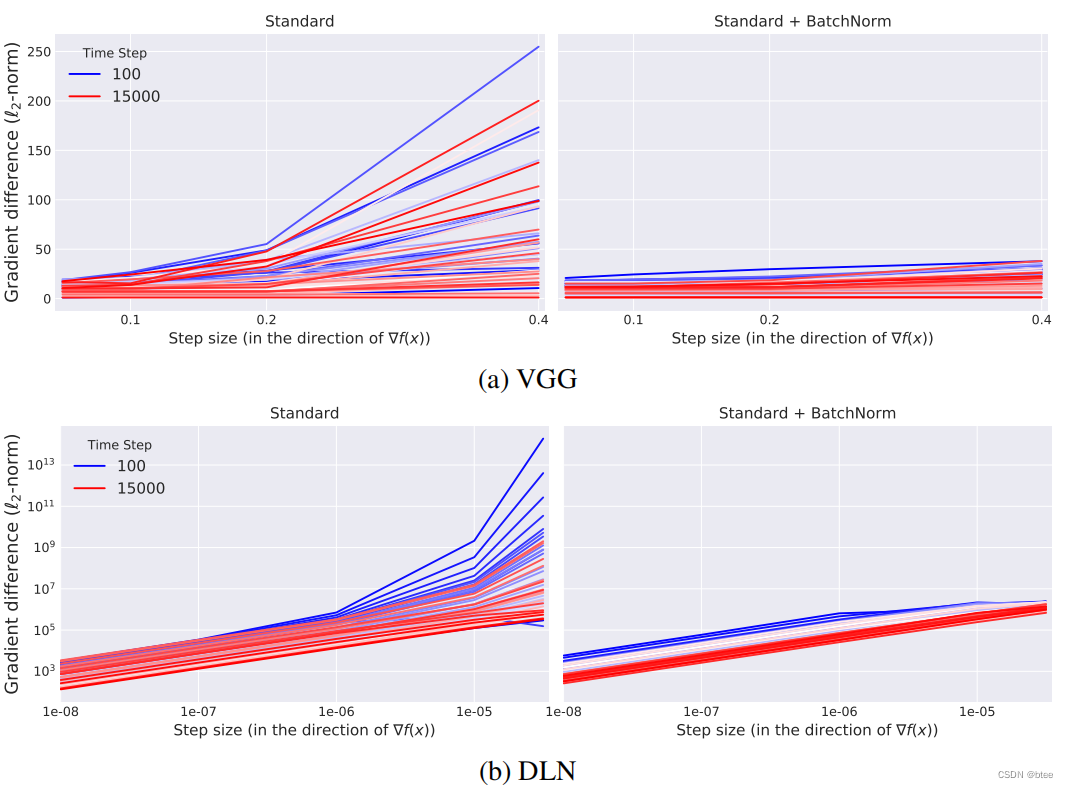
在VGG和DNN中加了BN都有改善
同时,作者还发现,BN不是唯一可以进行平滑optimization landscape的方式,再进行了不同正则化之后,网络的损失和梯度也能实现平滑
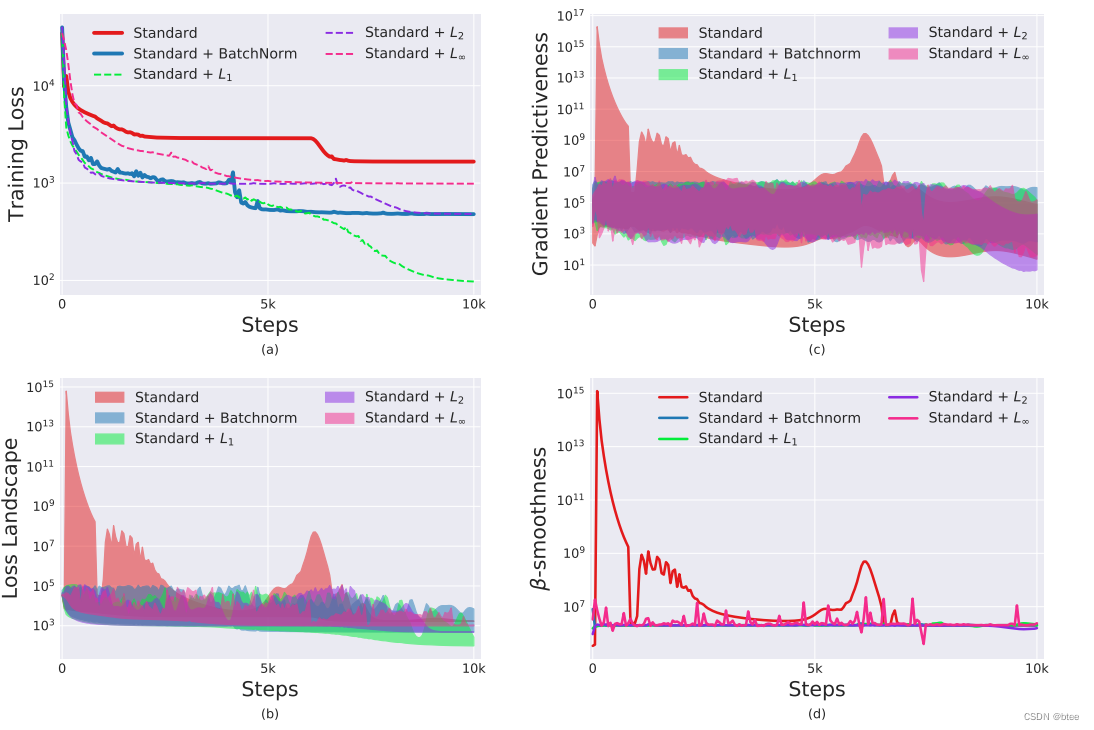
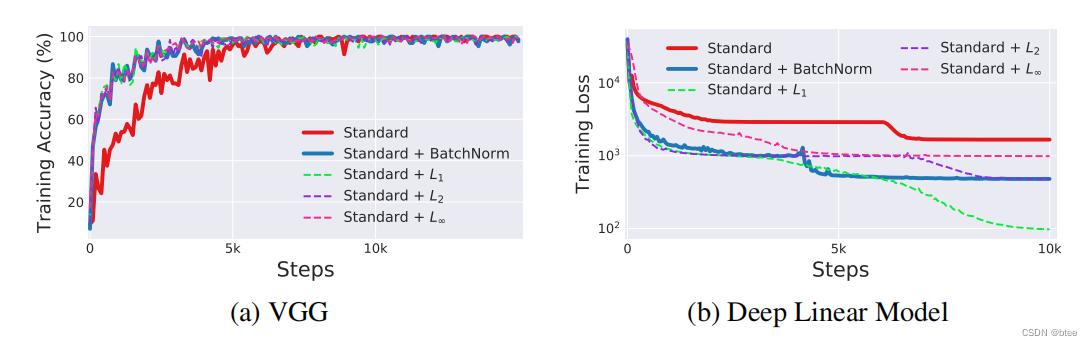
理论分析
作者还给出了BN为什么能实现平滑optimization landsacpe的公式推导
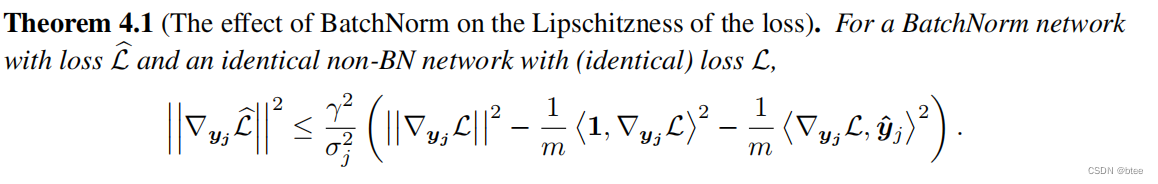
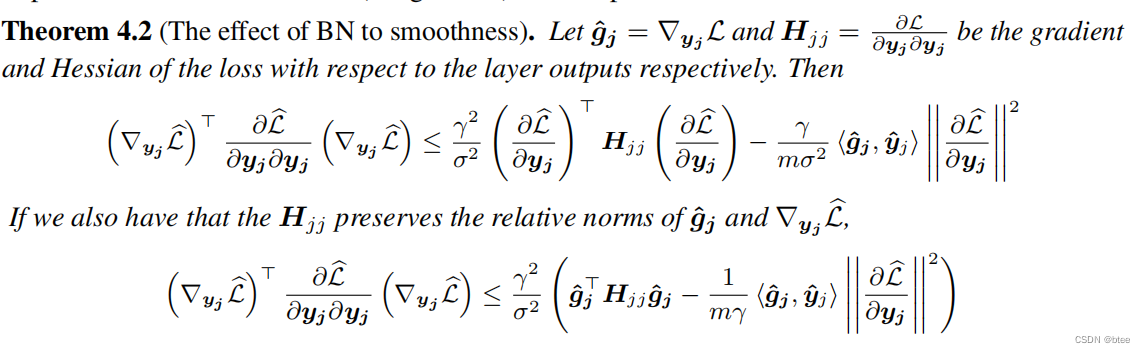


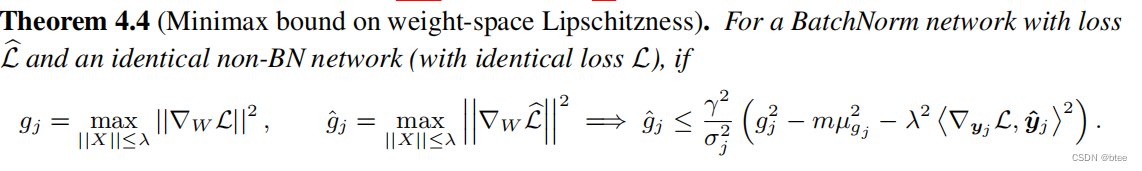

总结
很早期的标杆性论文,对理解BN层的作用很有帮助