---

提示：是正在努力进步的小菜鸟一只，如有大佬发现文章欠佳之处欢迎评论区指点~ 废话不多说，直接发车~

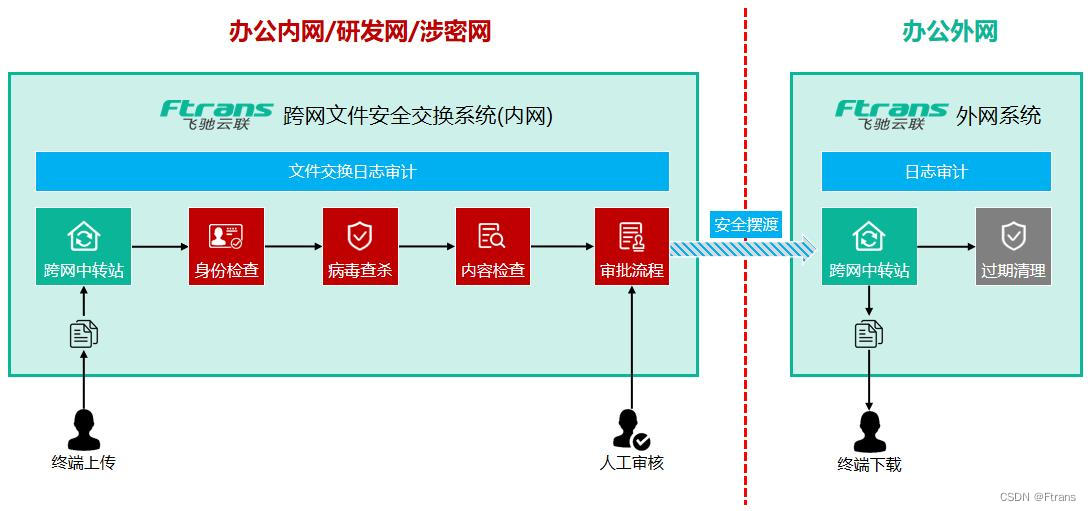
一、什么是优先级队列

优先级队列并不是像普通普通的队列那样永远遵从先进先出, 而是有优先级的, 出队时让优先级高的先出队

上篇文章说过, 二叉树是一种逻辑结构, 物理结构上可以是顺序存储, 也可以是链式存储, 而堆就是在顺序存储的二叉树上做了调整

PriorityQueue底层使用了堆这种数据结构

堆的概念:
如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

说人话:
1, 堆必须是完全二叉树
2, 每一棵树的根节点必须小于/大于左右孩子结点
如图: (小根堆+大根堆)

---

二、模拟实现

优先级队列底层是堆, 所以首先我们要实现堆这种数据结构, 堆的操作是在顺序存储的二叉树上, 换句话说就是在数组上, 所以成员属性只需要一个数组和用来记录长度的 usedSize 即可, 成员方法可以给定一个构造方法用来定义堆的容量大小

给定一个数组, 创建成堆, 自然需要把数组里的数据拷贝到堆底层的数组上来组织, 所以再设置一个成员方法用来初始化数组

public class MyPriorityQueue {

    public int[] elem;
    public int usedSize;

    public MyPriorityQueue () {
        this.elem = new int[10];
    }

    public void initElem(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
    }

为什么要模拟实现： 自己模拟实现 简易版的 栈的增删查改等主要功能，大致理解栈的设计思想
再对比学习 Java 提供的集合类当中的 PriorityQueue，在学习 Java 的 PriorityQueue常用方法的同时，也能学习源码的思想

---

1, 实现堆的基本操作

Java集合中的堆默认是小根堆, 我们模拟实现的堆也是小根堆

1.1, 创建堆

首先我们要把一个无序数组创建成一个堆

1.2.1, 向下调整

把一个无序数组创建成堆的方式是: 向下调整


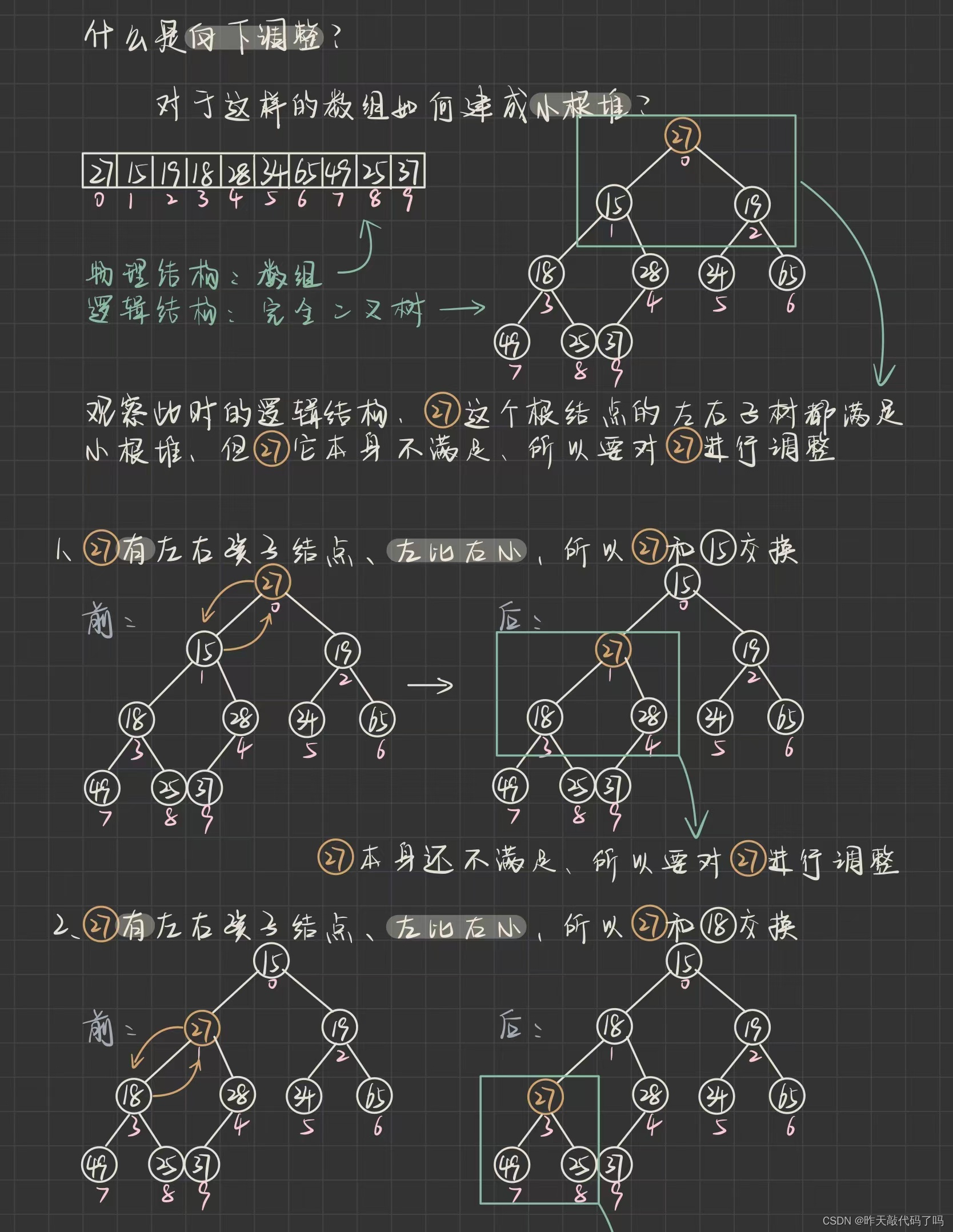
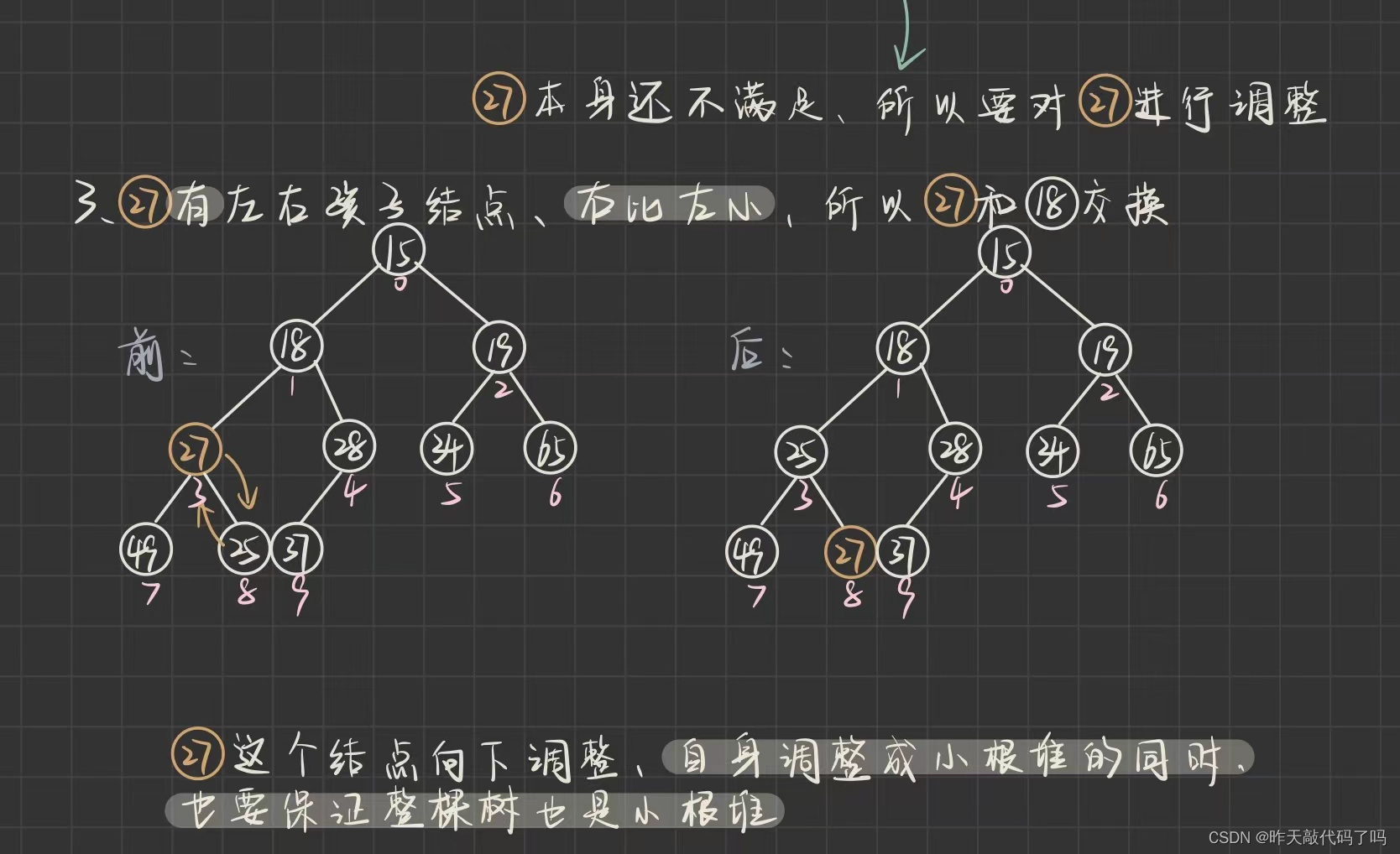
综上, 向下调整的规则是:
对于小根堆来说: 如果根结点大于左右孩子节点的其中一个
1, 待调整的结点定义为 parent , 被调整的结点定义为 child
2, child 选谁? 看图就知道, 是和左右孩子结点较小的那一个调整
3, 如果左右孩子存在的话, 根节点的下标是 i , 那么左孩子结点的下标就是 2i + 1, 右孩子的结点是2i + 2,

向下调整的代码:

    private void shiftDown(int parent,int len) {
        int child = 2*parent + 1;
        // 有左孩子就进入循环向下调整
        while (child < len) {
            // 如果有右孩子, 令child为较小的孩子结点
            if(child+1 < len && elem[child] < elem[child+1]) {
                child++;
            }
            if(elem[child] < elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                // parent中大的元素往下移动，可能会造成子树不满足堆的性质，因此需要继续向下调整
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }

仅供理解过程及思想, 没有使用泛型, Java中的PriorityQueue是需要使用泛型的, 而向下调整的过程涉及到两个数据的大小比较, 所以在使用PriorityQueue时需要指定对象的比较规则

向下调整的时间复杂度:
最坏情况下就是上图所示, 每调整完一次都需要继续向下调整, 直到树的最后一层(不再有孩子结点), 所以总体来说时间复杂度是O(log₂N)

---

了解了向下调整, 对数组建堆就好理解了, 但还有一个需要注意的点, 刚刚向下调整的前提是什么?
前提是, 左右子树已经是小根堆了 , 因为每次向下调整都是要进行比较的, 目的就是为了把更小的数据往堆顶放, 如果左右子树不满足小根堆, 你一趟向下调整, 不一定把最小的放上面了, 那这一趟不是白白浪费了吗

基于这一点, 对一组无序数据建堆的顺序应该是自下而上的进行向下调整
意思就是, 从最底下开始, 让底层的子树通过向下调整的方式建成小根堆, 再逐步往上推进, 这样就能保证每一次向下调整, 当前根结点的左右子树都满足小根堆
如图:

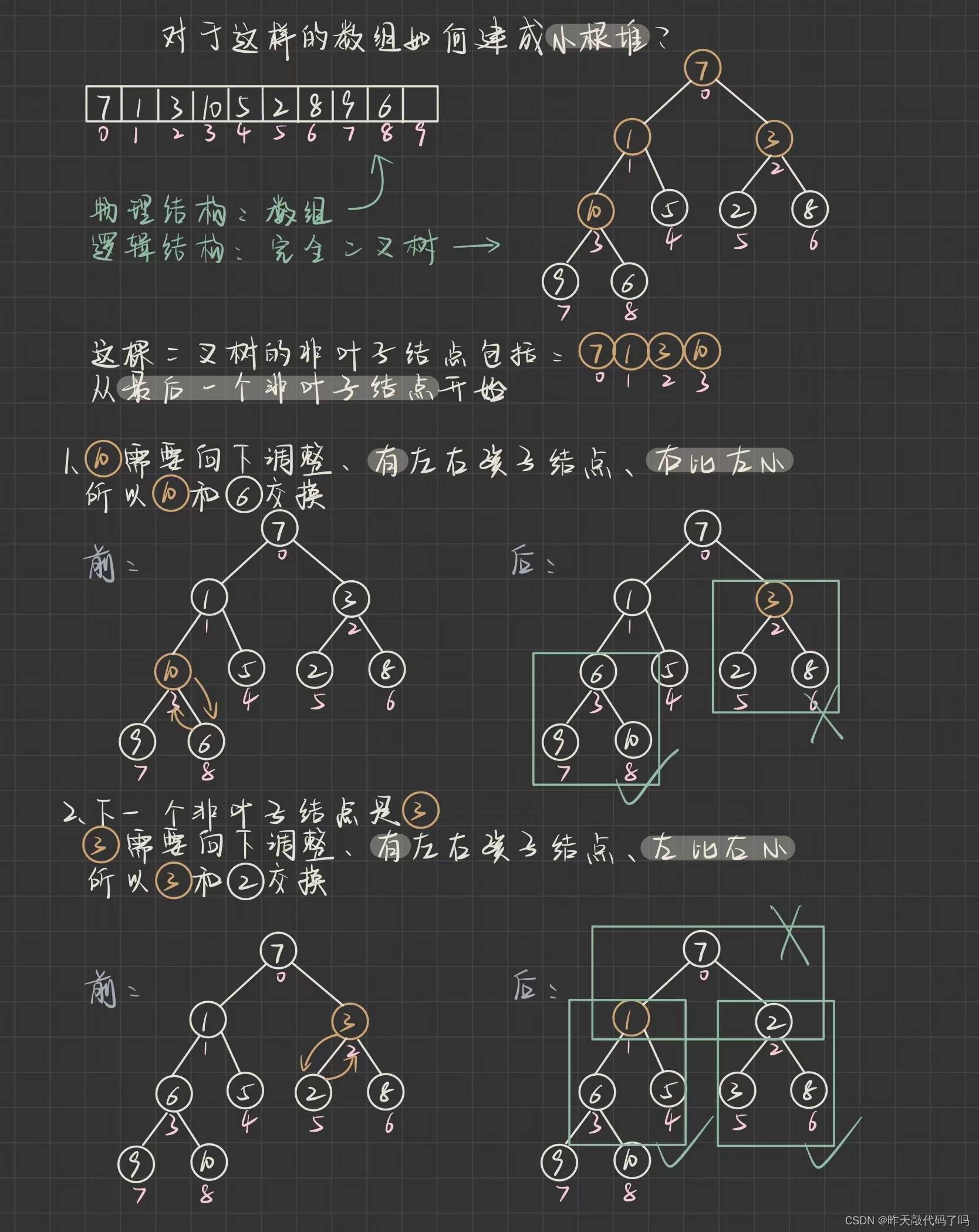
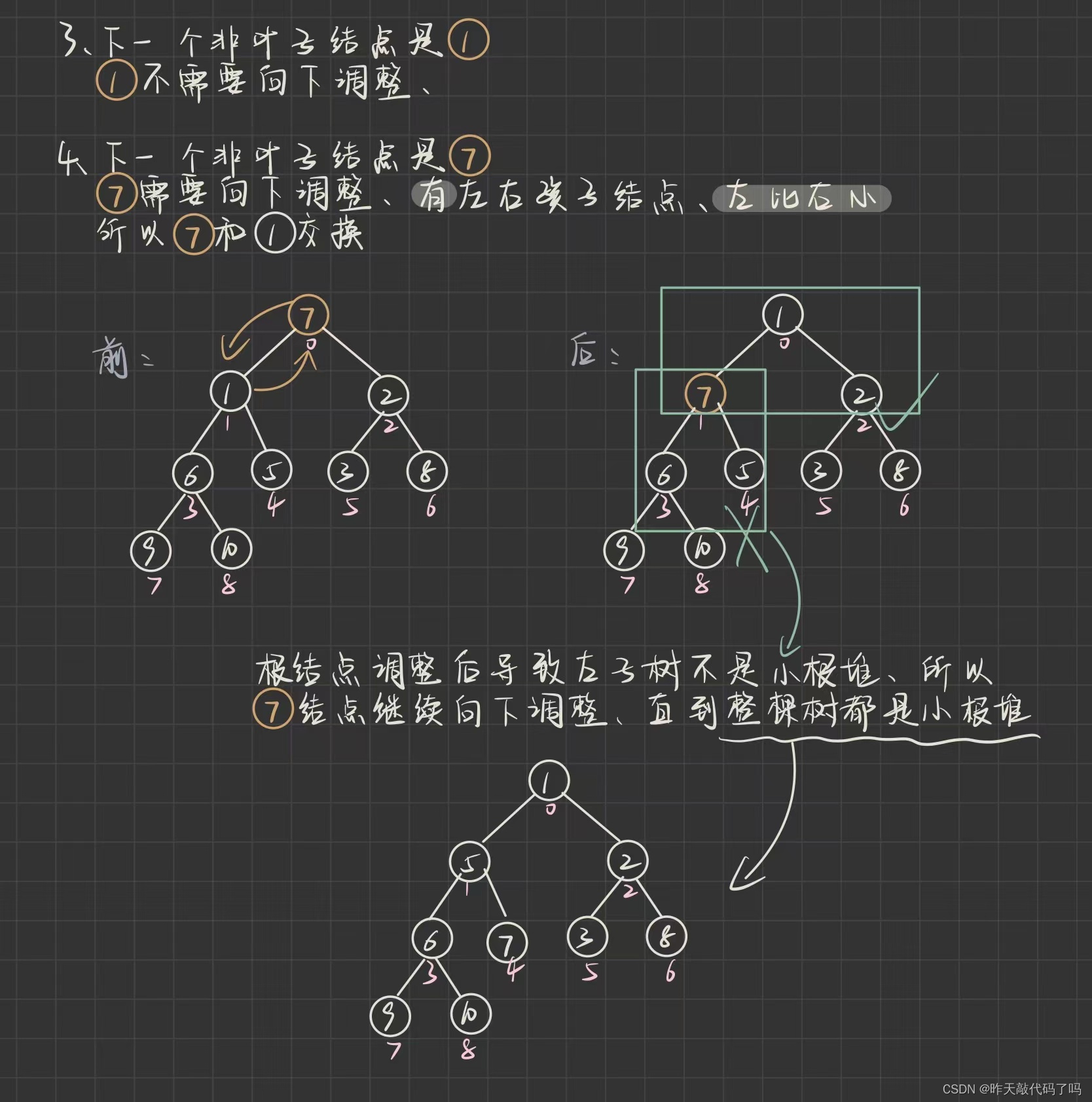
上图过程演示了自下而上执行向下调整, 如果某次向下调整导致子树不满足小根堆, 要继续向下调整(如上图最后一步)

上述过程就是一个从最后一个非叶子结点开始的循环, 问题是如果编写成代码, 循环的条件是什么呢? 如何确定最后一个非叶子结点的下标呢?

上图中, 最后一个非叶子结点的下标是3, 最后一个结点就是它的右孩子结点, 下标是8, 那么: (8-1)/2 得到 3 , 正式其父结点的下标, 如果不存在有孩子, 那至少有左孩子, (7-1)/2 得到 3

最后一个非叶子结点的右(左)孩子下标就是数组长度 - 1, 所以确定最后一个非叶子结点的下标方法就是((array.length-2)>>1);

观察上图, 什么时候不再需要向下调整呢? 当非叶子结点是0下标的结点时, 退出循环

综上, 建堆的代码如下:

    public void createHeap() {
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            shiftDown(parent,usedSize);
        }
    }

上面说过, 向下调整的时间复杂度是O(log₂N), 而利用向下调整建堆的时间复杂度是O(N)

数学公式推导出来的~

---

1.2, 堆的插入

堆的操作是在数组上, 那么插入一个数据应该放在哪里呢? 当然是数组末尾, 那么二叉树就会多出一个叶子节点, 插入数据后仍要保持整棵树是一个大根堆, 那么就需要进行向上调整

1.2.1, 向上调整

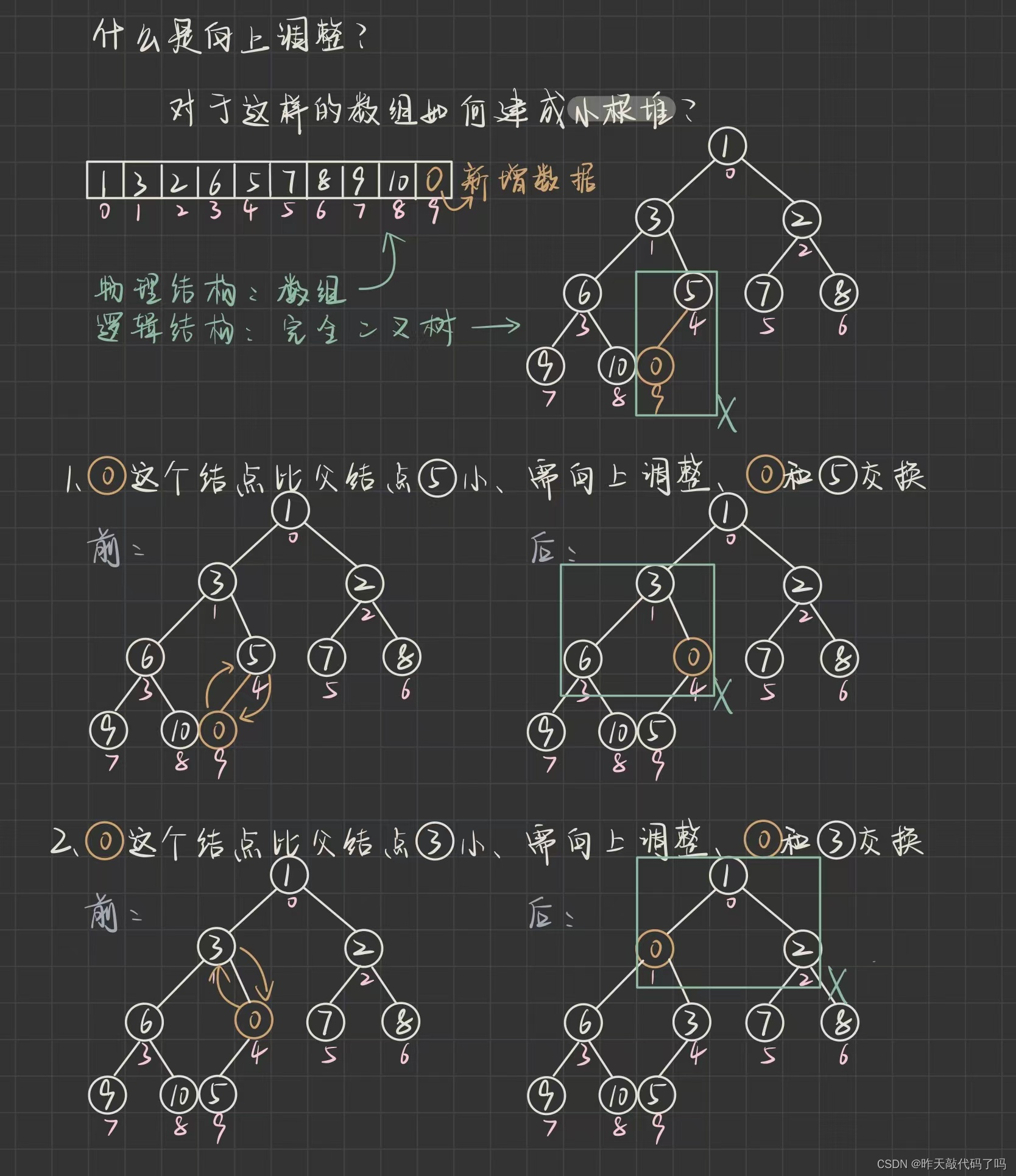
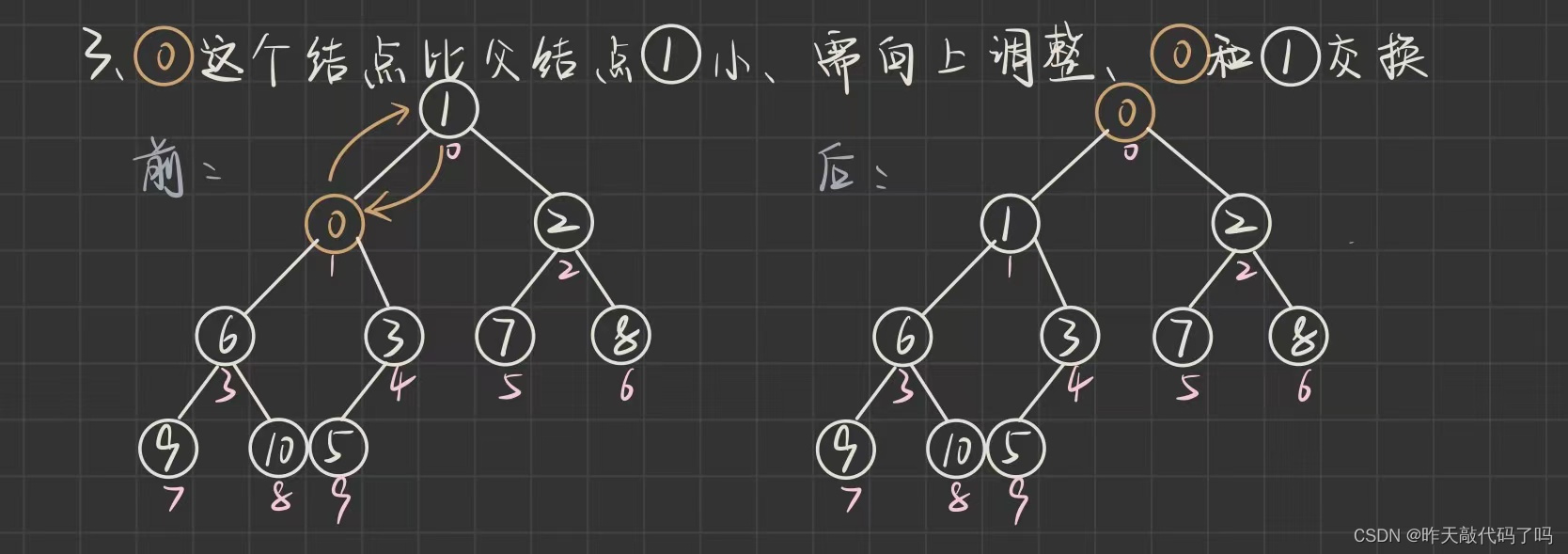
代码如下:

    private void shiftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if(elem[child] < elem[parent]) {
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child-1)/2;
            }else {
                break;
            }
        }
    }	

---

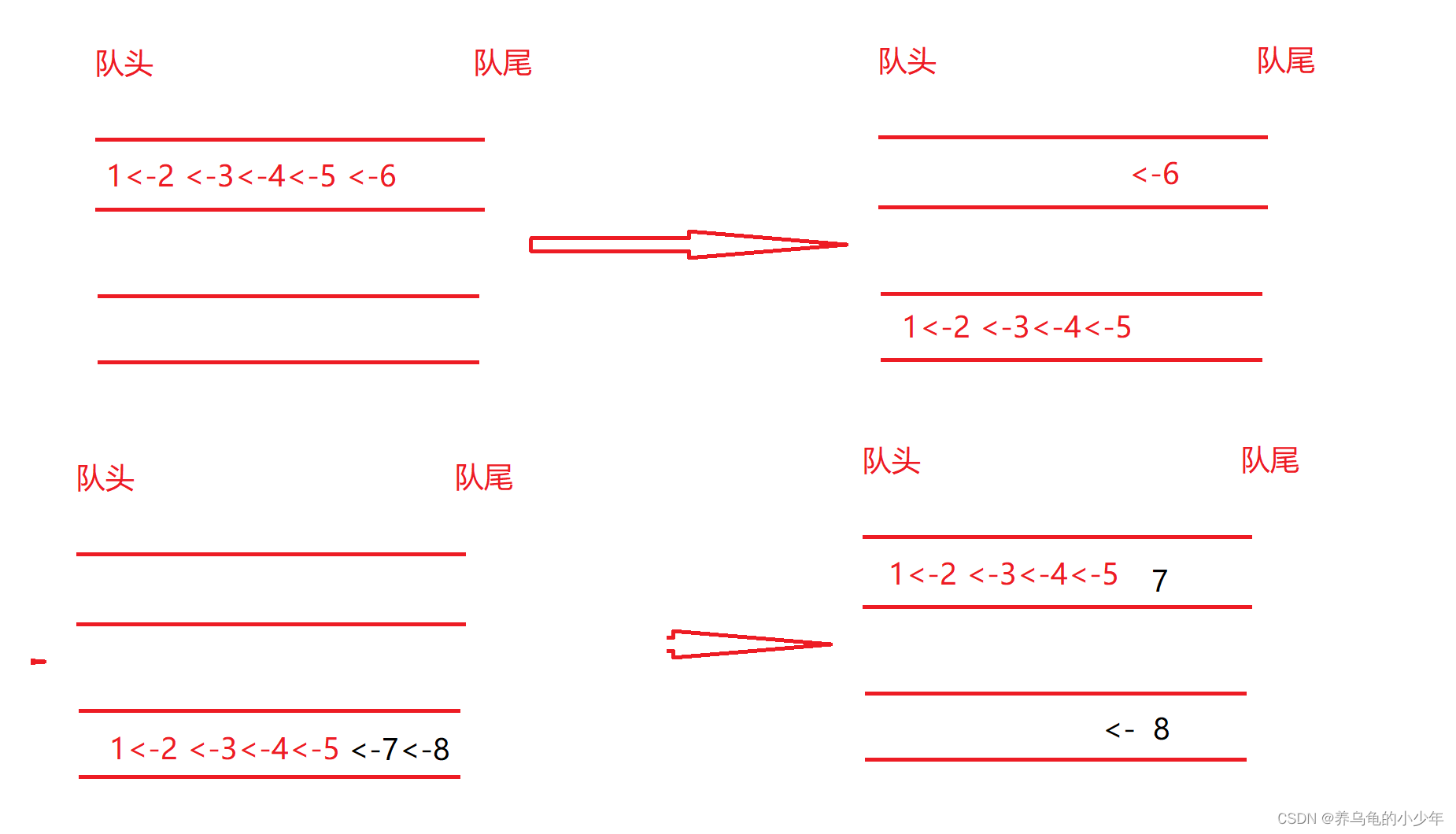
1.2, 堆的删除

堆的删除是删除堆顶(堆顶(最小或最大), 所以优先级最高), 把堆顶数据和最后一个结点数据交换, 然后对交换后的对顶元素向下调整, 直到整棵树都变成小根堆


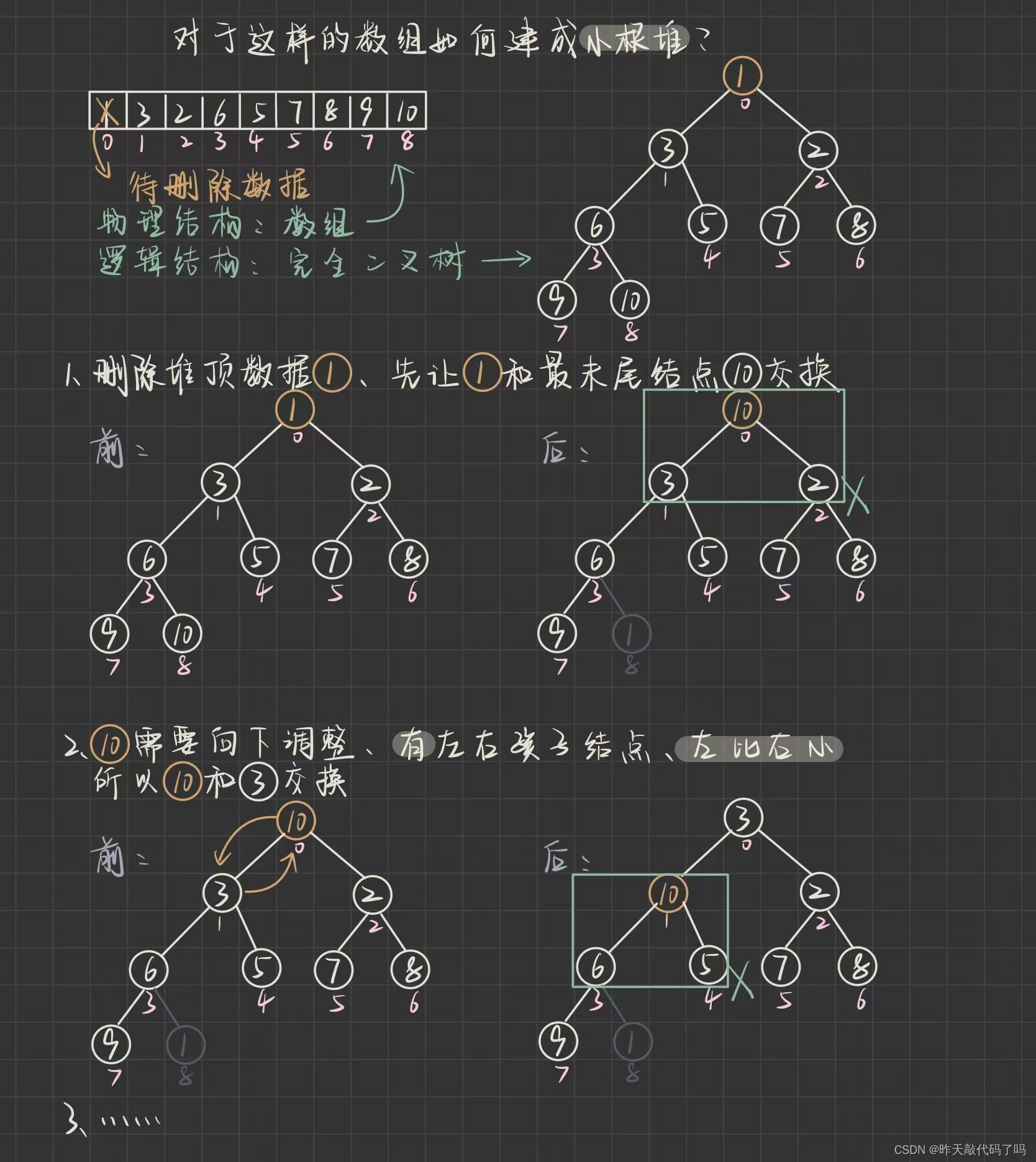
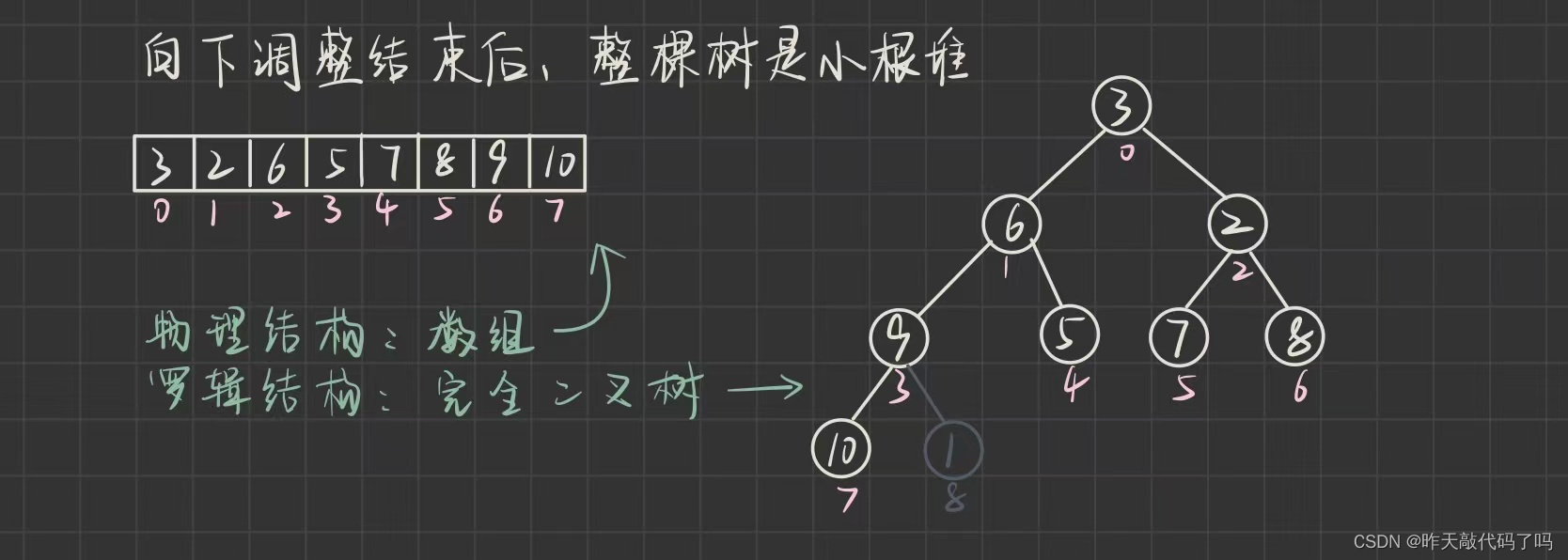
那么剩最后一个下标为8的结点怎么办呢, 别忘了 usedSize 是用来记录优先级队列中的长度的, 在优先级队列中删除数据之后, usedSize自减一次, 即代表堆中有效数据减少一个

回顾一下向下调整的代码, 每一个结点向下调整的限制是 child 下标值< len

---

清楚了堆的创建, 插入和删除, 实现优先级队列的插入和删除就很简单了

2, 实现优先级队列

2.1, offer – 插入数据

老规矩, 插入前先判满, 如果满了要扩容
插入之后 usedSize要自加一次

    public void offer(int val) {
        if(isFull()) {
            //扩容
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize++] = val;//11
        //向上调整
        shiftUp(usedSize-1);//10
    }
    public boolean isFull() {
        return usedSize == elem.length;
    }

---

2.1, poll – 删除数据

老规矩, 删除前要先判空, 如果为空, 不能继续删除

public void pop() {
        if(isEmpty()) {
            return;
        }
        swap(elem,0,usedSize-1);
        usedSize--;
        shiftDown(0,usedSize);
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }
    
    private void swap(int[] array,int i,int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
}

---

三、Java提供的PriorityQueue

1, PriorityQueue说明

PriorityQueue 实现了 Queue 这个接口

注意事项:
PriorityQueue 中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出 ClassCastException 异常
不能插入 null 对象，否则会抛出 NullPointerException

因为PriorityQueue 中插入删除的数据是泛型类, 可以是基本类型对应的包装类, 也可以是自定义类, 在向上调整和向下调整的过程中, 需要不断地比较, 如果数据没有指定比较规则, 或者为null时, 程序就会抛出异常

没有容量限制，可以插入任意多个元素，其内部可以自动扩容

任意多个是相对来说的, 类类型的数据存放在堆中, 所以数据个数最多不能超过堆的内存大小, 链表同理

插入和删除元素的时间复杂度为 O(log₂N)

---

2, 使用PriorityQueue

2.1, PriorityQueue实例化方式

无参构造法 底层数组默认容量是11

        Queue<Integer> priorityQueue1 = new PriorityQueue<>();

整形数据作为参数, 设置化底层数组容量

        Queue<Integer> priorityQueue2 = new PriorityQueue<>(10);

比较器(匿名内部类对象)作为参数传参, 设置push方法中的向上调整时两数据比较规则

        Queue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });

Java集合中的 PriorityQueue 底层的堆默认是小根堆, 如果要设置大根堆, 就必须传入比较器, 并重写 compare 方法, 如上代码所示

---

2.2, PriorityQueue常用方法

在 main 方法中展示使用方式：

        Queue<Integer> priorityQueue = new PriorityQueue<>();
        int[] array = {1,3,2,6,5,7,8,9,10,0};
        for(int x : array) {
            // 1, 插入数据
            priorityQueue.offer(x);
        }
        // 2,获取优先级最高的数据
        int ret1 = priorityQueue.peek();
        System.out.println("获取优先级最高的数据:" + ret1);

        // 3,删除优先级最高的数据
        int ret2 = priorityQueue.poll();
        System.out.println("删除优先级最高的数据:" + ret2);

        // 4,获取优先级队列中数据个数
        int size = priorityQueue.size();
        System.out.println("数据个数:" + size);

        // 5, 清空优先级队列
        priorityQueue.clear();

        // 6, 查看队列是否为空
        boolean bl = priorityQueue.isEmpty();
        System.out.println("队列是否为空:" + bl);
    }

运行结果:

---

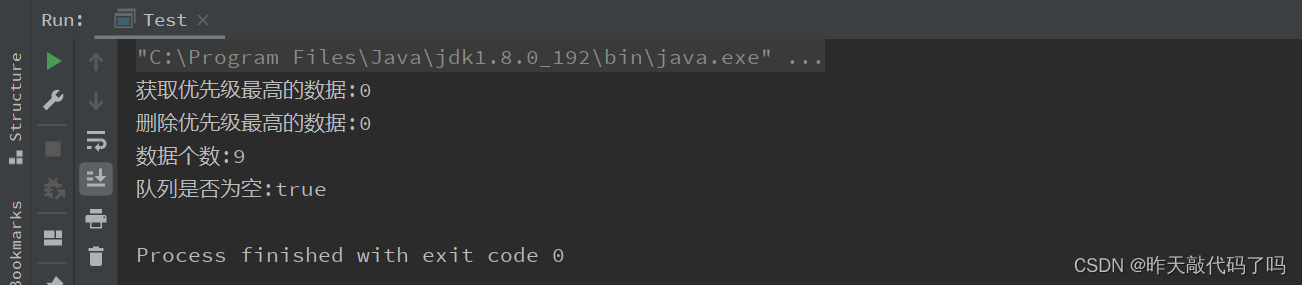
总结

以上就是今天分享的关于数据结构中【优先级队列】的内容
一方面介绍了如何模拟实现简易的优先级队列以及(小根堆)堆的实现方式，一方面介绍了Java集合框架中的【PriorityQueue】类的基本使用

思考分析: 堆中的向下调整和向上调整有什么区别? 建堆为什么需要自下而上的向下调整,以及删除堆顶数据需要向下调整, 而插入数据需要向上调整?

以小根堆为例:
1, 向下调整是父节点和左右孩子结点比较, 向上调整是当前结点和父结点比较, 向下调整和向上调整都是为了把小的数据往堆顶移动, 大的数据往堆底移动

2, 建堆的过程中自下而上是为了从"下面"出发, 不断的把目前最小的数据网上移动, 每次都需要向下调整是为了保证最小数据移动到堆顶的同时, 左右子树也要保持小根堆
删除数据的过程中, 由于要让优先级最高的数据出队, 所以要舍弃堆顶, 和末尾数据交换后向下调整 , 重建小根堆
插入数据的过程中, 每次在末尾入队一个数据, 它没有左右子树, 不可能向下调整, 只能不断和父结点比较, 寻找这个新结点的合适位置

如果本篇对你有帮助，请点赞收藏支持一下，小手一抖就是对作者莫大的鼓励啦🤪🤪🤪

---

上山总比下山辛苦
下篇文章见