代码随想录第四十二天| ● 01背包问题，你该了解这些！ ● 01背包问题，你该了解这些！滚动数组 ● 416. 分割等和子集

news2024/11/25 10:32:33

01背包问题

模型详解

描述
在一个容量有限的背包里装若干物品，这些物品重量不同，价值不同。如何装使这些背包内物品价值最大。
（1）如果物品可以分割，直接用贪心算法，首先装价值密度最大的物品
（2）如果物品不能分割，使用==动态规划 ==
01背包与完全背包的区别
0,1：每件物品只能用一次，要么不装，要么只装一次
多重背包：每件物品可以装多次
0,1背包递推公式详解

在这里插入图片描述

（1）dp【i】【j】：从0，i中任取物品，放到容量为就j的背包里，最大价值。
（2）递推公式
对于第i件物品，可以选择不放，也可以选择放
dp【i】【j】=max（dp【i-1】【j】，dp【i-1】【j-w【i】】+v【i】）
（3）
初始化
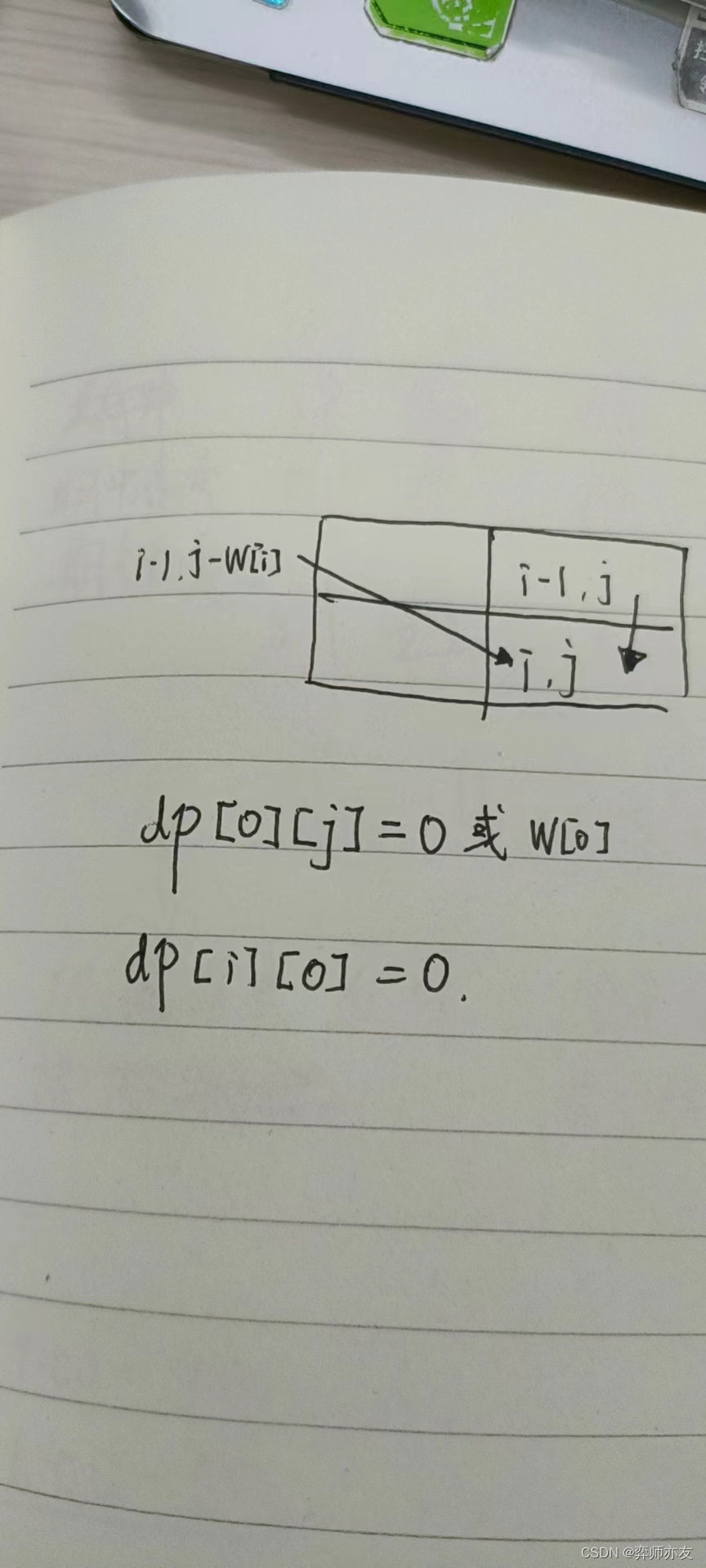
在这里插入图片描述

（5）略

代码

    // 01背包二维数组
public int testWeightBagProblem01(int[] weight, int[] value, int bagSize){
    int[][] dp = new int[weight.length][bagSize+1];// dp[i][j]从 0-i中选取物品放到容量为j的背包的最大价值
    // 初始化
    for (int i = 0; i < dp.length; i++) {
        dp[i][0]=0;
    }

    for (int i = 0; i <=bagSize; i++) {
        if (weight[0]>i){
            dp[0][i]=0;
        }else {
            dp[0][i]=value[0];
        }
    }

    // 递归
    for (int i = 1; i <dp.length ; i++) {
        for (int j = 0; j <=bagSize ; j++) {
            if (weight[i]>j){
                dp[i][j]=dp[i-1][j];
            }else {
                dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
            }
        }
    }
    return dp[weight.length-1][bagSize];

    }

滚动数组代码

j从右往左遍历，可以将二维数组化简为一维数组
在这里插入图片描述

```// 02背包滚动数组
    public int testWeightBagProblem02(int[] weight, int[] value, int bagSize){
        int[] dp = new int[bagSize+1];// dp[i][j]从 0-i中选取物品放到容量为j的背包的最大价值
        // 初始化
        for (int i = 0; i <=bagSize; i++) {
            if (weight[0]>i){
                dp[i]=0;
            }else {
                dp[i]=value[0];
            }
        }

        // 递归
        for (int i = 1; i <weight.length ; i++) {
            for (int j = bagSize; j >=0 ; j--) {
                if (weight[i]>j){
                    dp[j]=dp[j];
                }else {
                    dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]);
                }
            }
        }
        return dp[bagSize];

    }

分割等和子集

在这里插入图片描述

看完题后的思路

这是一个0,1背包问题，背包的容量是 sum（元素）/2,物品是元素，重量是元素的值，价值也是元素的值。===> 在所有物品中挑选元素，在满足背包ronglde前提下，使价值最大，判断最大价值是否等于背包容量
（如果装满，最大价值一定等于背包容量，因为价值密度为1）

代码

// 416 分割子集
    public boolean canPartition(int[] nums) {
        int sum=0;
        for (int num : nums) {
            sum+=num;
        }
        if (sum%2==1){
            return false;
        }
        int bagSize=sum/2;
        int[] dp = new int[bagSize + 1];
        // 初始化
        for (int j = 0; j <=bagSize; j++) {
            if (j<nums[0]){ // 重量
                dp[j]=0;
            }else {
                dp[j]=nums[0];// 价值
            }
        }
        for (int i = 1; i <nums.length ; i++) {
            for (int j = bagSize; j >=0 ; j--) {
                if (nums[i]>j){
                    dp[j]=dp[j];
                }else {
                    dp[j]= Math.max(dp[j],dp[j-nums[i]]+nums[i]);
                }
            }
        }
        
        return dp[bagSize]==bagSize;


    }