图解LeetCode——剑指 Offer 46. 把数字翻译成字符串

news2024/11/18 9:10:51

一、题目

给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

二、示例

2.1> 示例 1:

【输入】 12258
【输出】 5
【解释】 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

提示：

0 <= num < 2^31

三、解题思路

根据题目描述，我们要将数字翻译为字符串，那么对于一个数字来说，都可以找到一一相对应的字母；但是，如果是两个数字以上的话，就不一定了，针对数字12就有如下翻译方式：

【1个数字翻译1次】1——>b，2——c；那么最终12可以被翻译为“bc”；
【2个数字被翻译】那么最终12可以被翻译为“m”；

但是，如果两个数字超过了25，那么就无法被按照整体翻译了，只能一个数字翻译一次，以26为例：

2——>c；6——>g；那么最终26可以被翻译为“cg”；

通过上面的解释，大家其实可以看出一个解题思路，那就是把输入的数字进行“拆分”，看最终能合理拆分出多少种；

我们再继续分析，虽然一个数字有很多的“位”，但是其实每次进行合并后是否超过了25的对比行为都只涉及到两个相邻的数字，即：第i位与第i-1位，那么我们就可以通过这两位是否合并，来动态的计算出总的翻译结果了。具体请见下图所示，我们以输入：12258为例，看一下具体的对比过程。

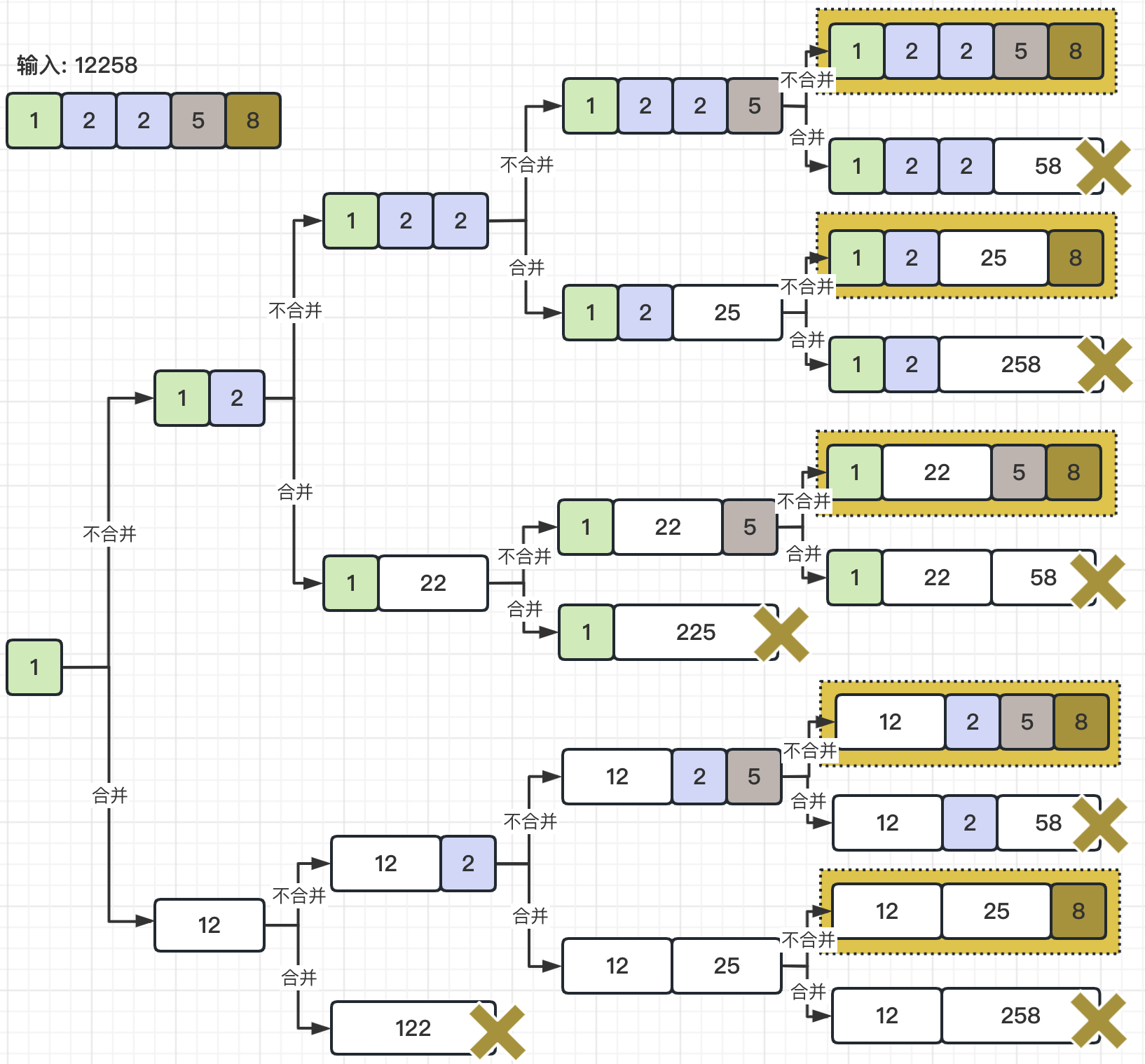
看完上面的对比过程，我们就可以推导出动态转移公式了，即：

【如果i可以与i-1合并】dp[i] = dp[i-1] + dp[i-2];
【否则】dp[i] = dp[i-1];

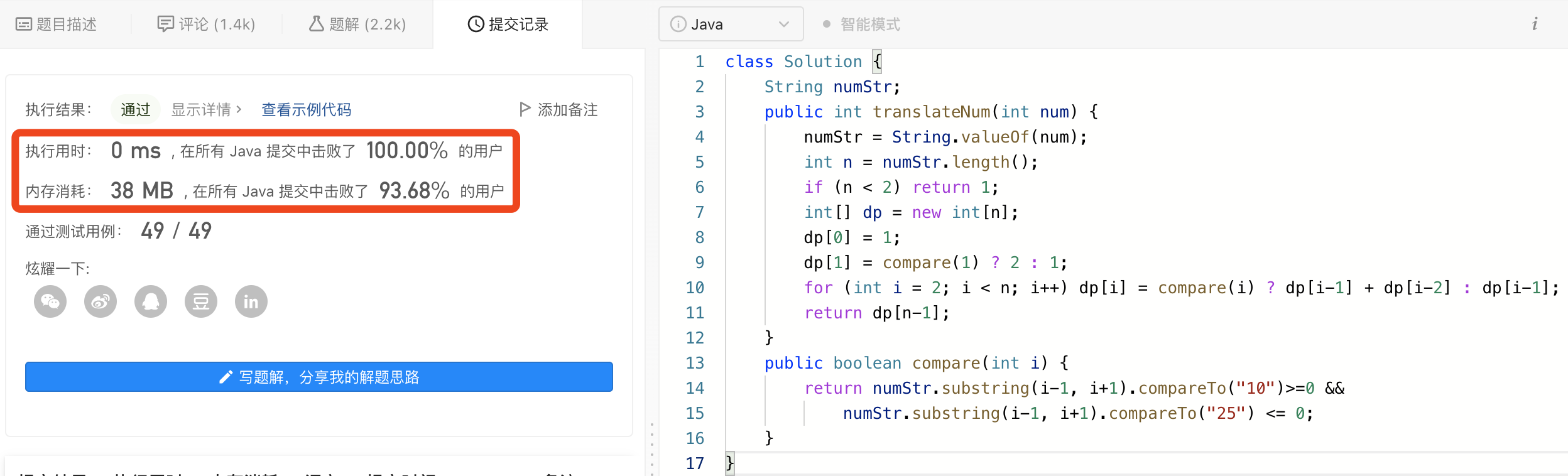
四、代码实现

class Solution {
    String numStr;
    public int translateNum(int num) {
        numStr = String.valueOf(num);
        int n = numStr.length();
        if (n < 2) return 1;
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = compare(1) ? 2 : 1;
        for (int i = 2; i < n; i++) dp[i] = compare(i) ? dp[i-1] + dp[i-2] : dp[i-1];
        return dp[n-1];
    }
    public boolean compare(int i) {
        return numStr.substring(i-1, i+1).compareTo("10")>=0 && 
            numStr.substring(i-1, i+1).compareTo("25") <= 0;
    }
}