小黑子的线代系列：第一章

1. 行列式

n×n数表确定的一种算式

1.1 二阶行列式

(2)二阶行列式是一种算式,它是两项的代数和:

• 一个是从左上角到右下角的对角线(又叫主对角线)上两个元素的乘积,取正号;
• 另一个是从右上角到左下角的对角线(又叫副对角线)上两个元素的乘积,取负号．
• 即计算遵循对角线法则:主对角线元素的乘积减去副对角线元素的乘积．如图所示,实线取正号,虚线取负号.

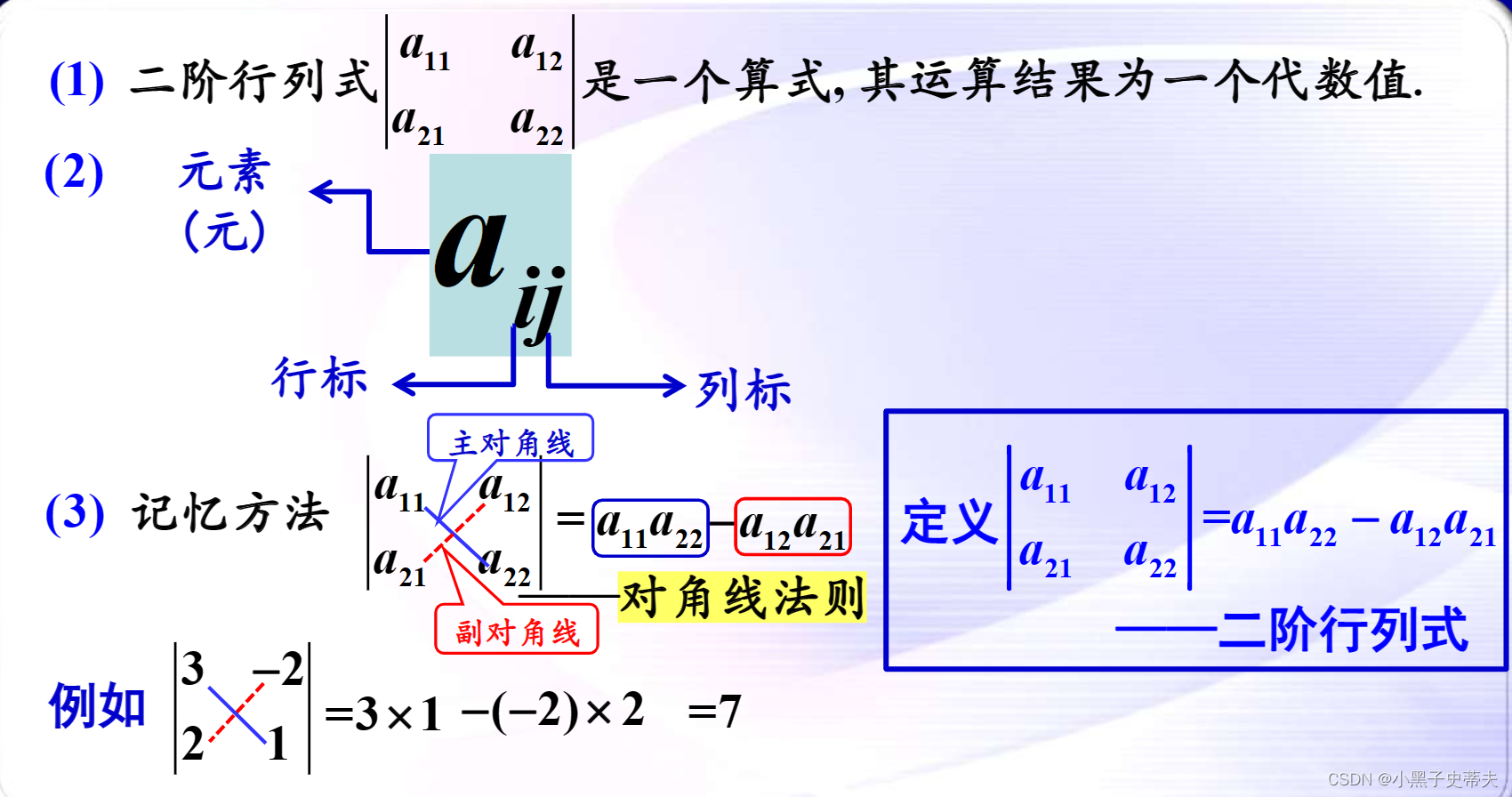
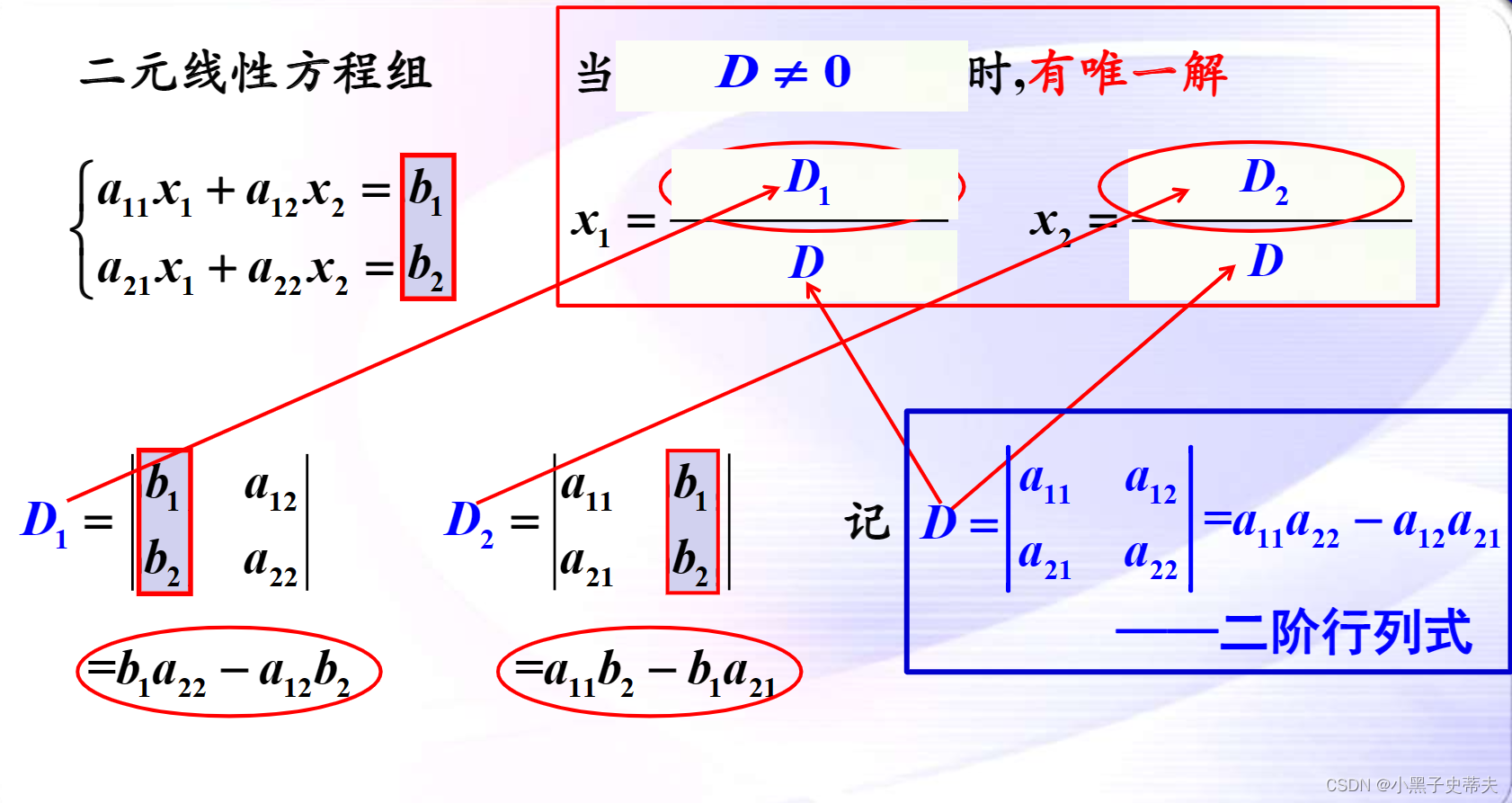
二阶行列结构分析：

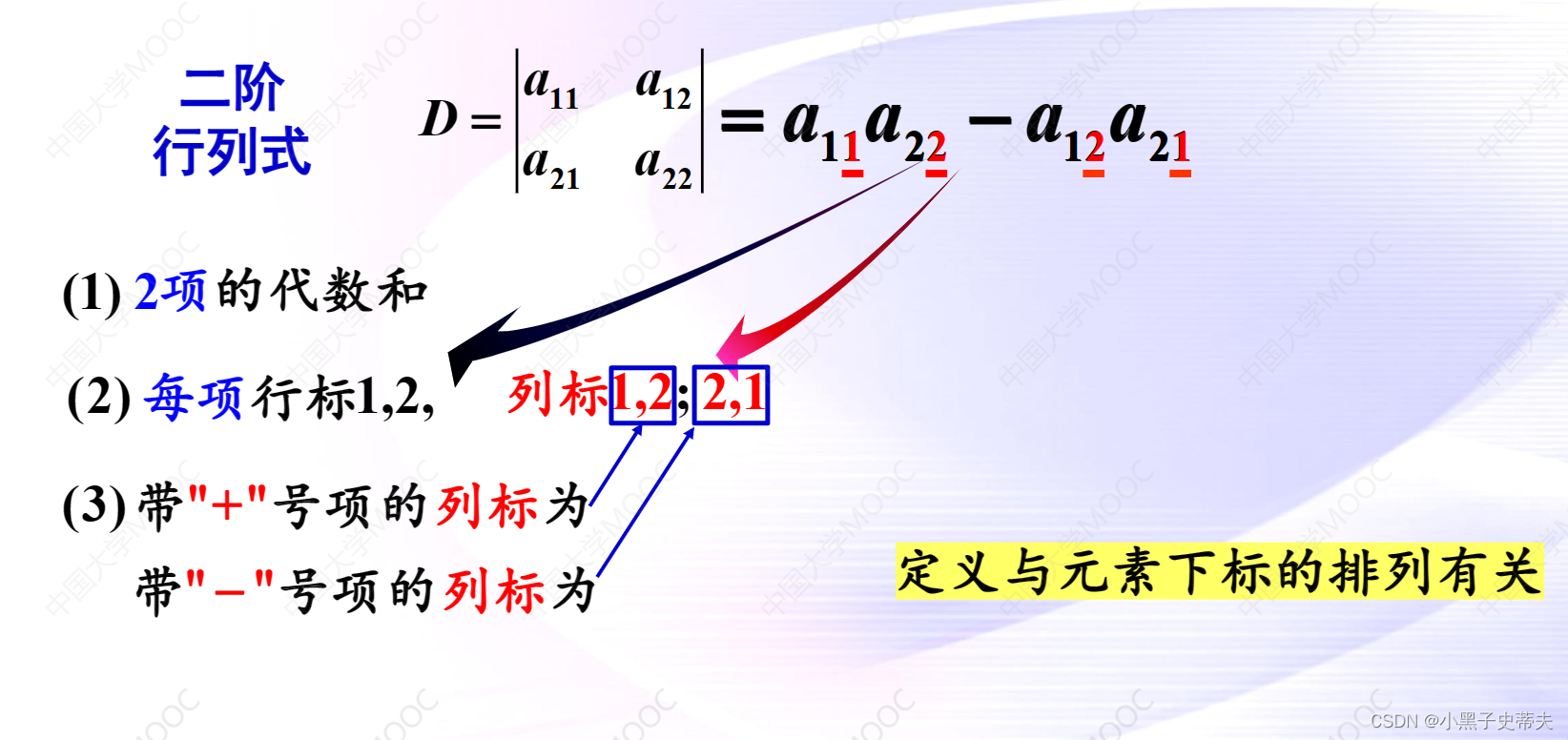
1.2 三阶行列式

三阶行列式计算同样遵循对角线法则:主对角线元素的乘积减去副对角线元素的乘积．如图所示,实线取正号,虚线取负号.

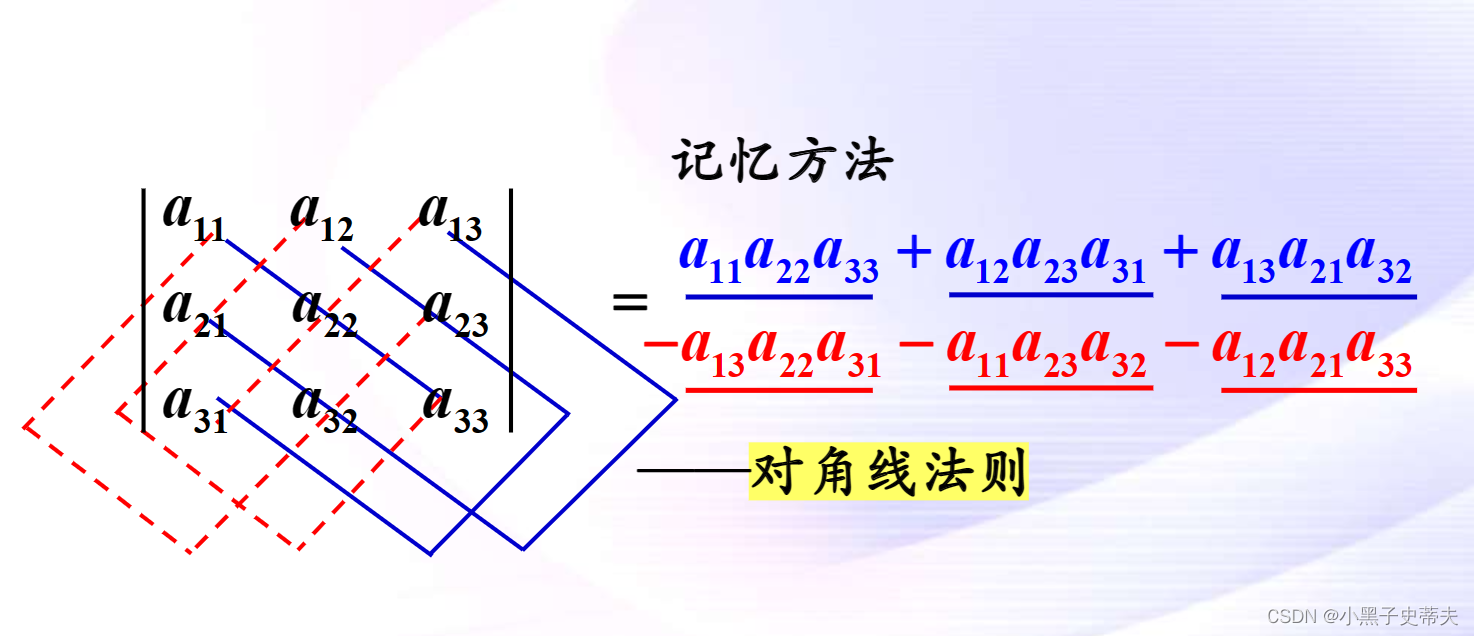
但是注意，对角线法制对四阶行列以上的不适用

三阶行列结构分析：

1.3 小结

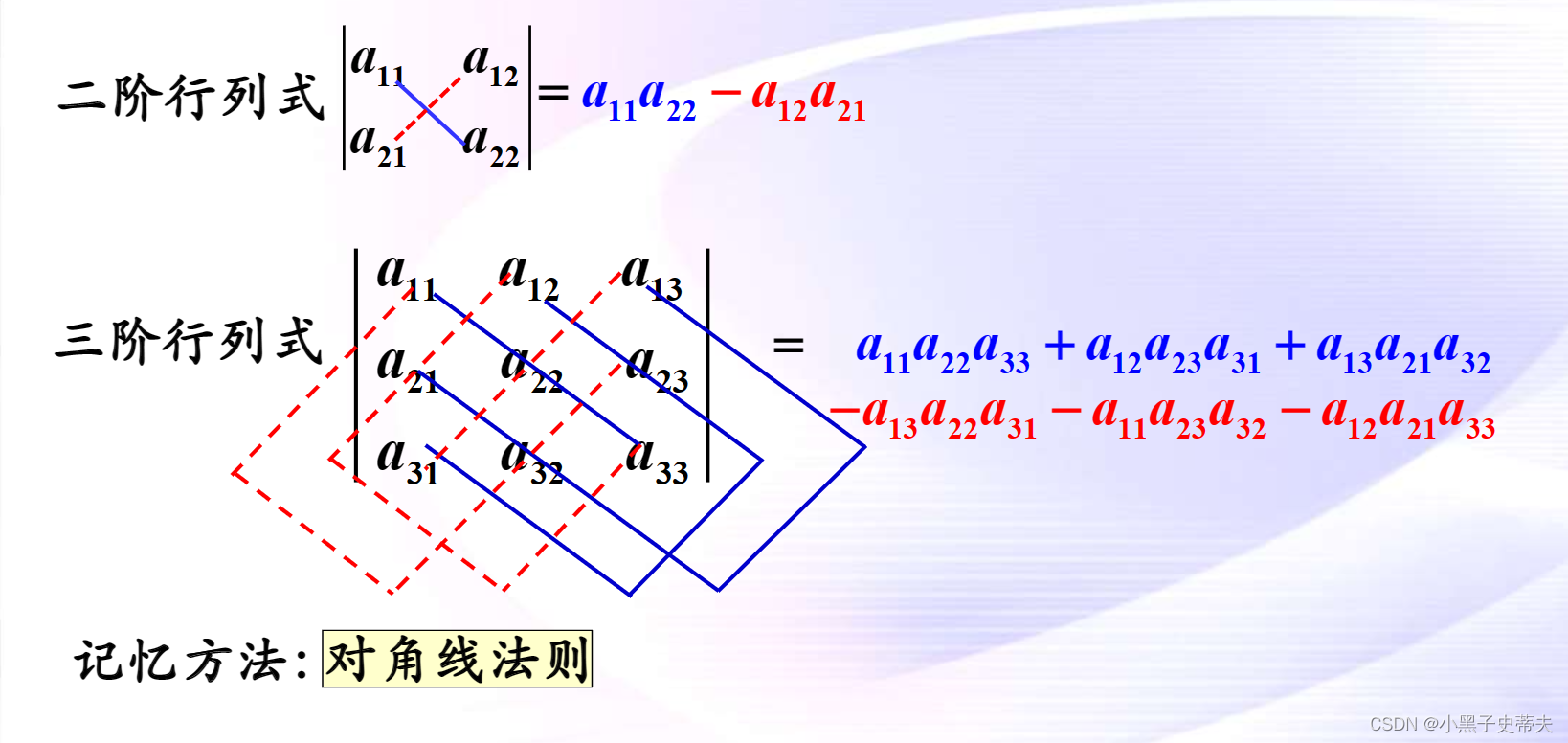
2. 全排列与逆序数

2.1 全排列

定义把n个不同的元素排成一排,叫做这n个元素的全排列,简称排列.共n!种

规定各元素之间有个标准次序.
比如:n个自然数的标准次序为:由小到大1,2,…,n

数字由小到大的n级排列1234…n称为自然序排列

2.2 逆序数

Γ、γ：读作gamma

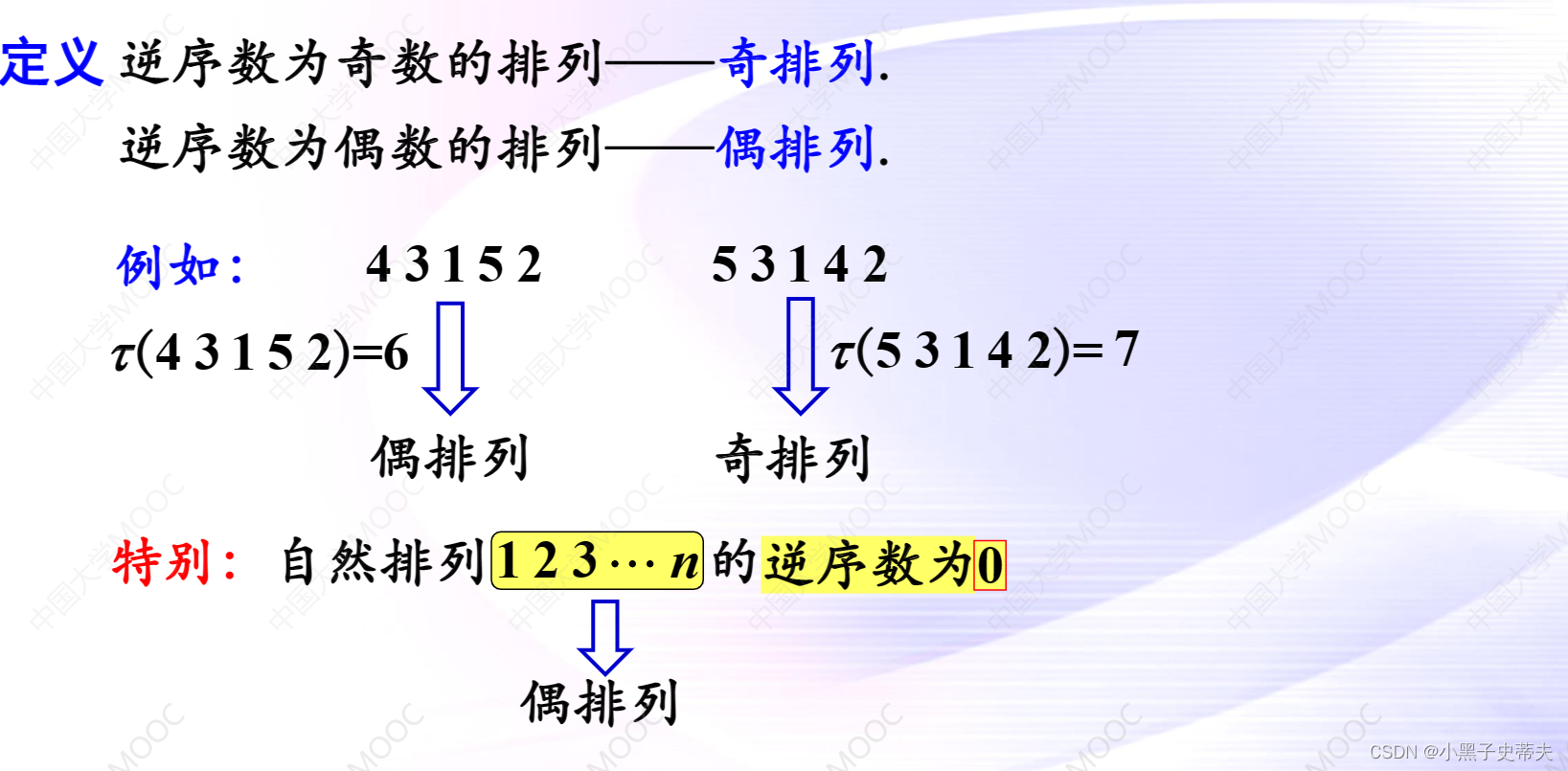
例题：

3. 对换

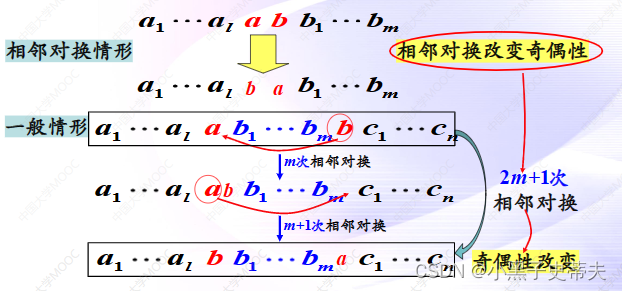
定理:
在所有的n级排列中(n≥2) ,奇排列与偶排列
的个数相等,各为n!/2个.

案例：

4. n阶行列式的定义

分析：

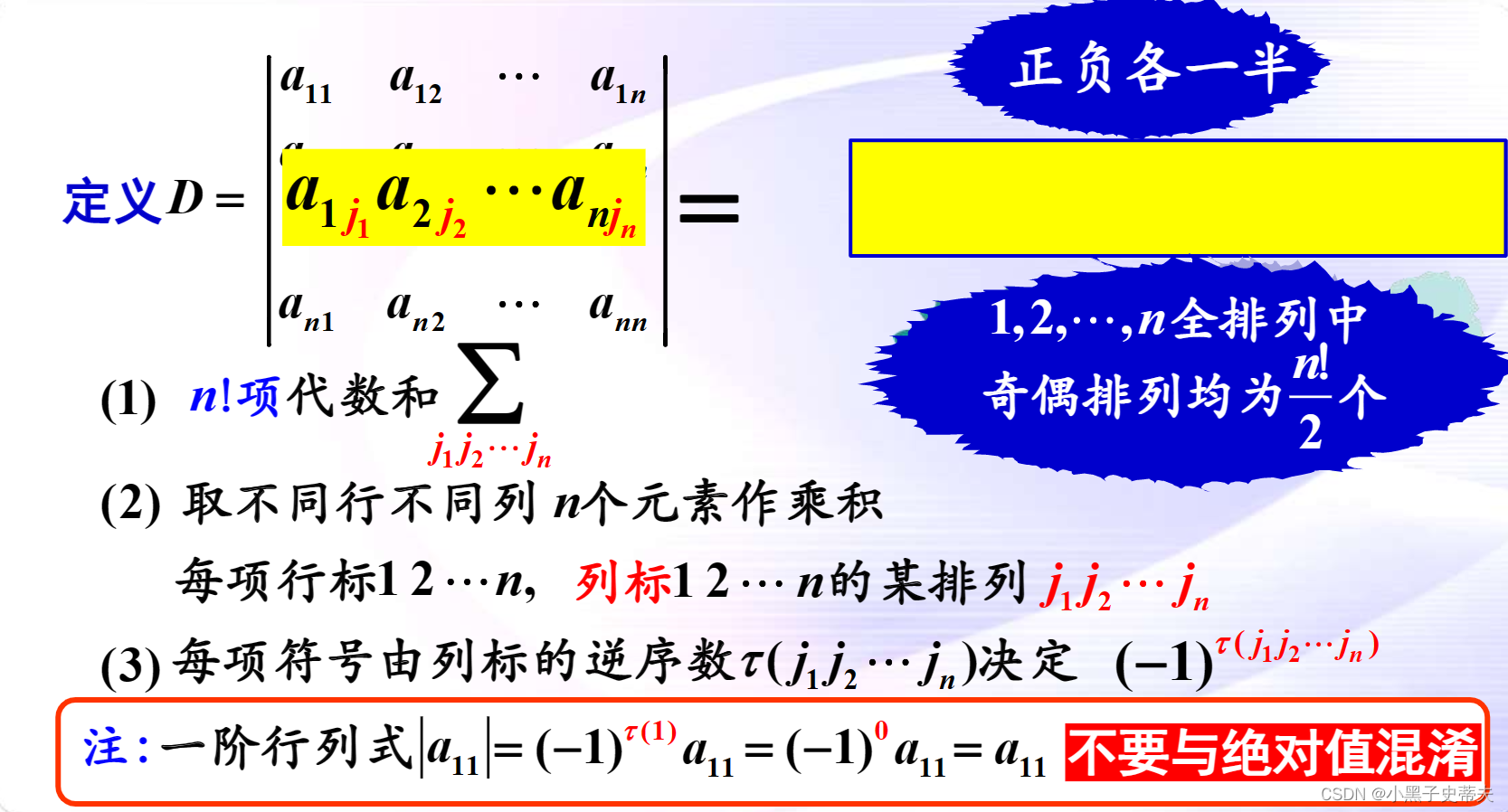
n阶行列式的定义：

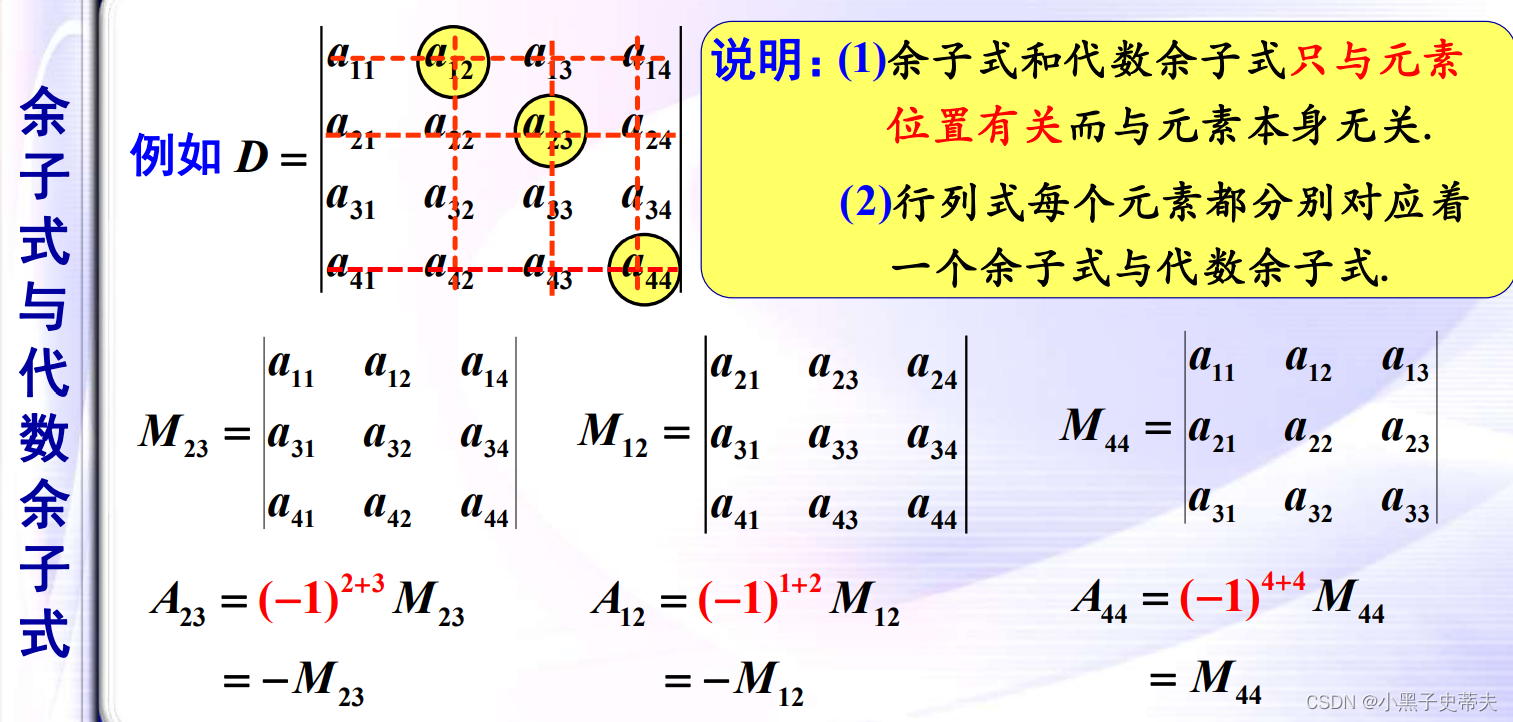
5. 余子式和代数余子式

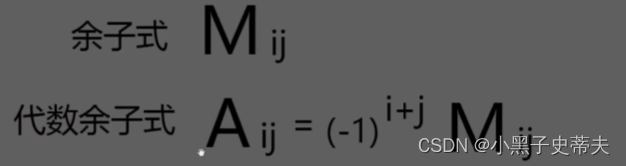
余子式

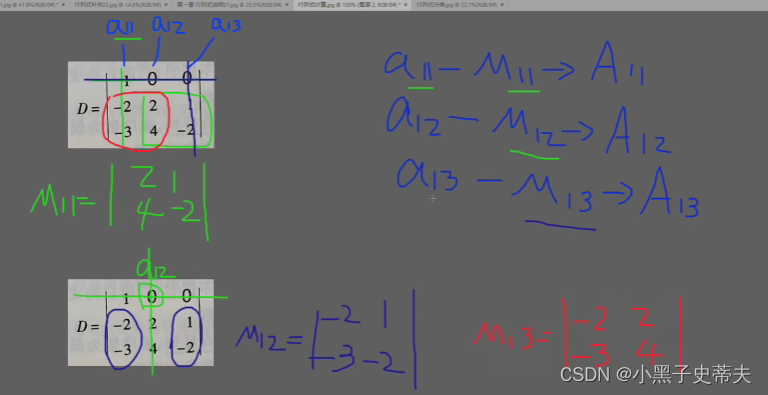
代数余子式

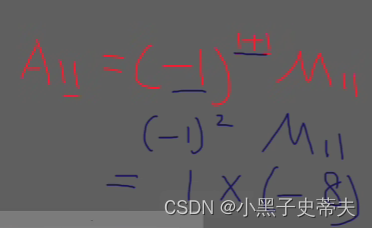
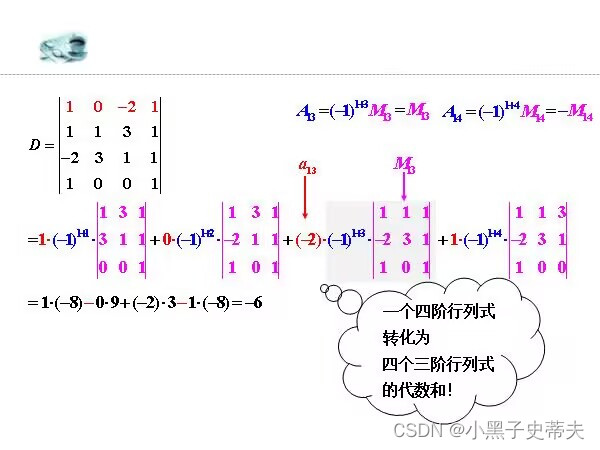
四阶案例：

6. 行列式的性质

6.1 转置行列式

简单来说就是行转换为列

• 性质1：行列式与它的转置行列式相等,即D= D’.

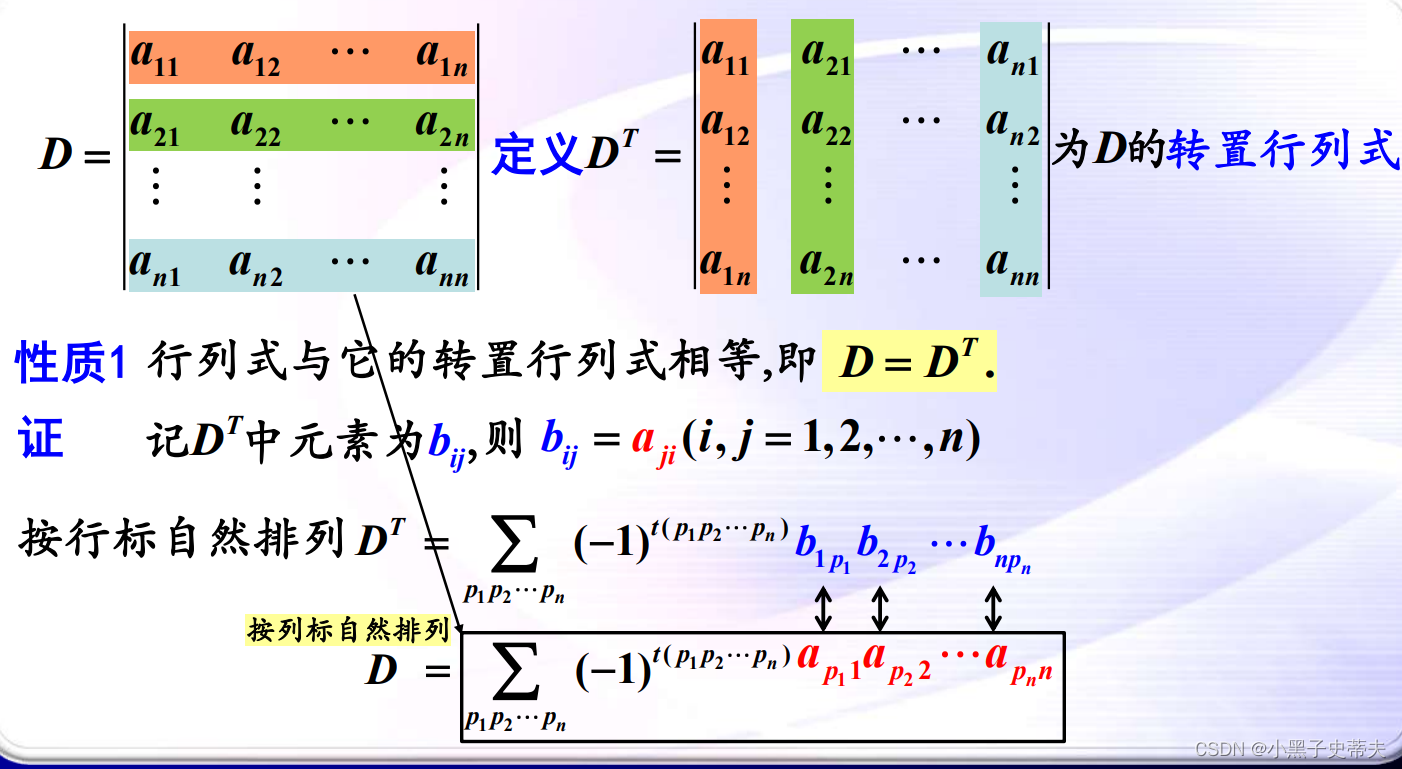
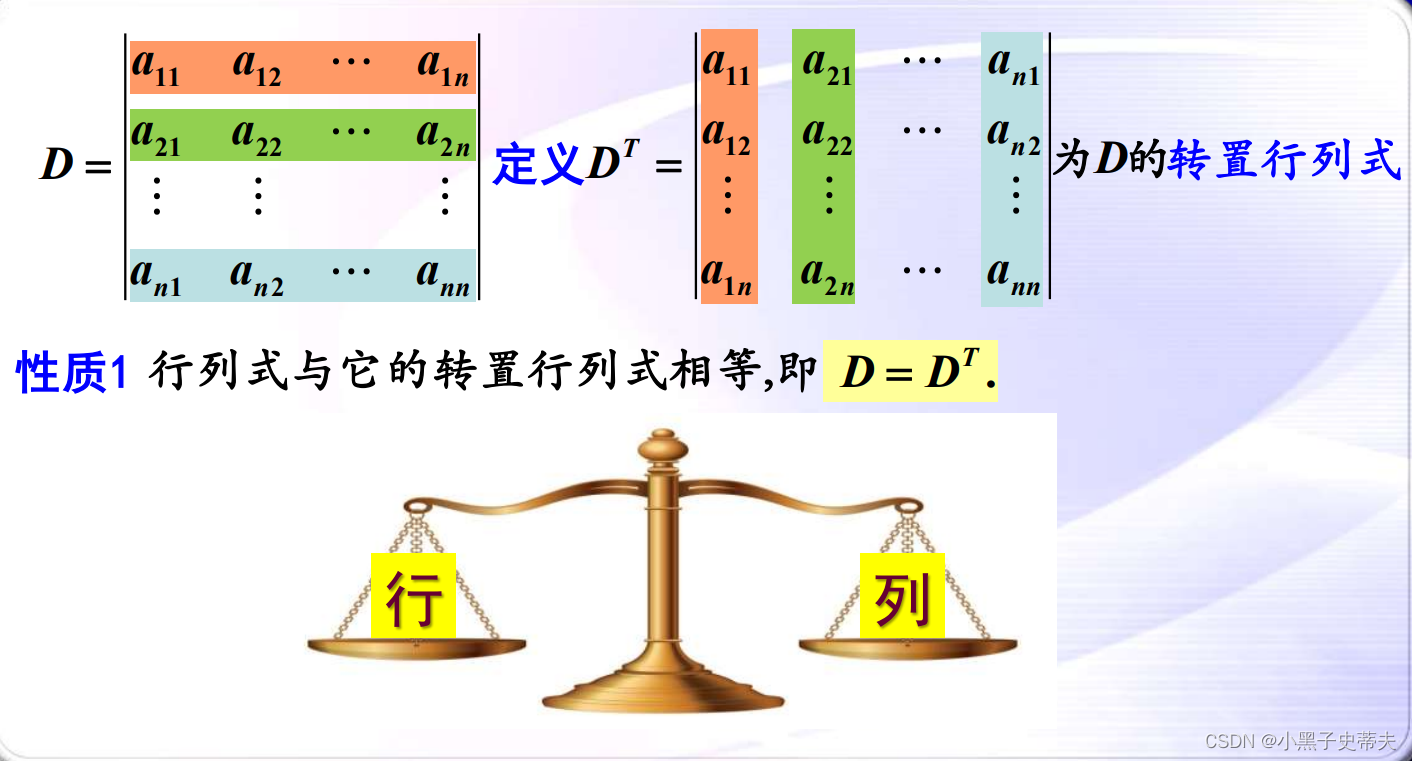
6.2 对换变号

• 性质2：互换行列式D的任意两行(或列),D的值变号.

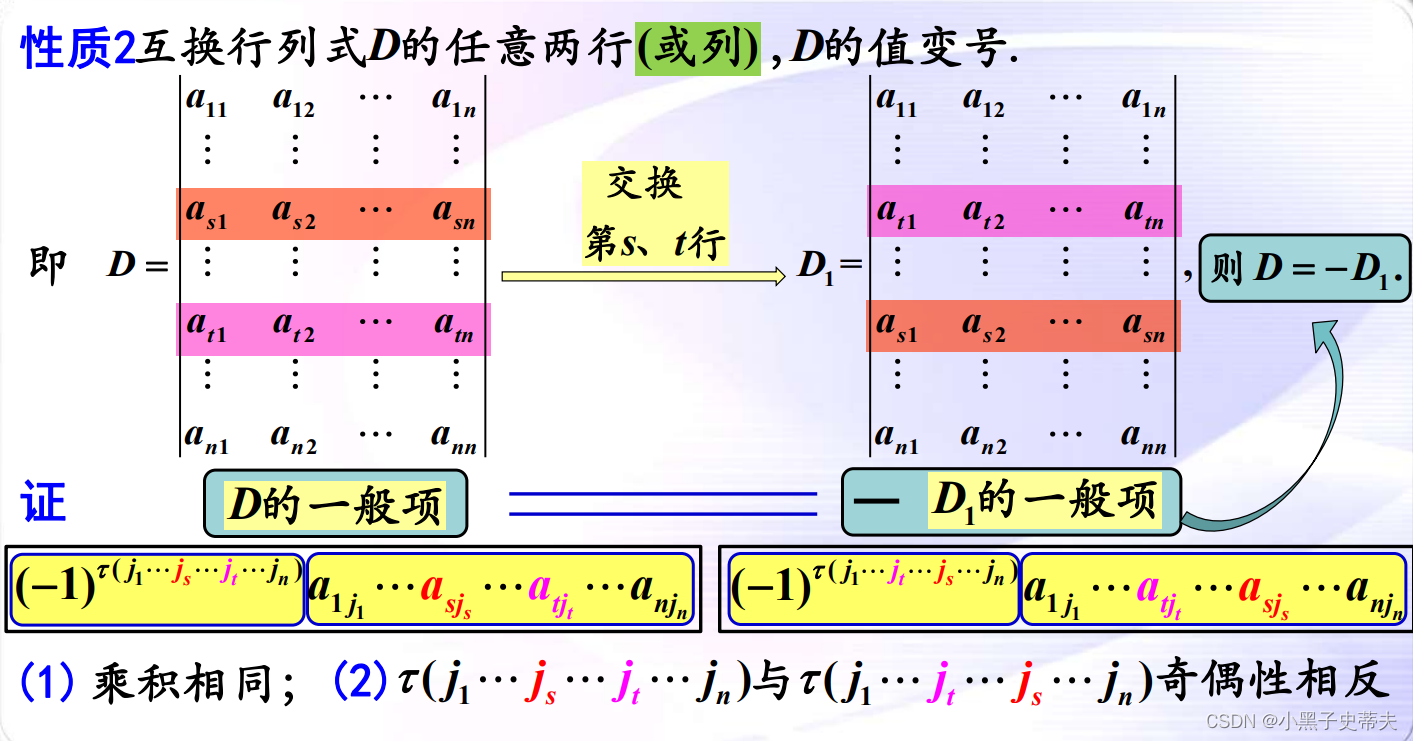
6.3 提取公因子

• 性质3：行列式D的某一行(或列)所有元素都乘以数k,等于k乘以D.

推论：

1. 某行（列）全为0,行列式的值为0
2. 某两行（列）元素对应成比例,行列式的值为0

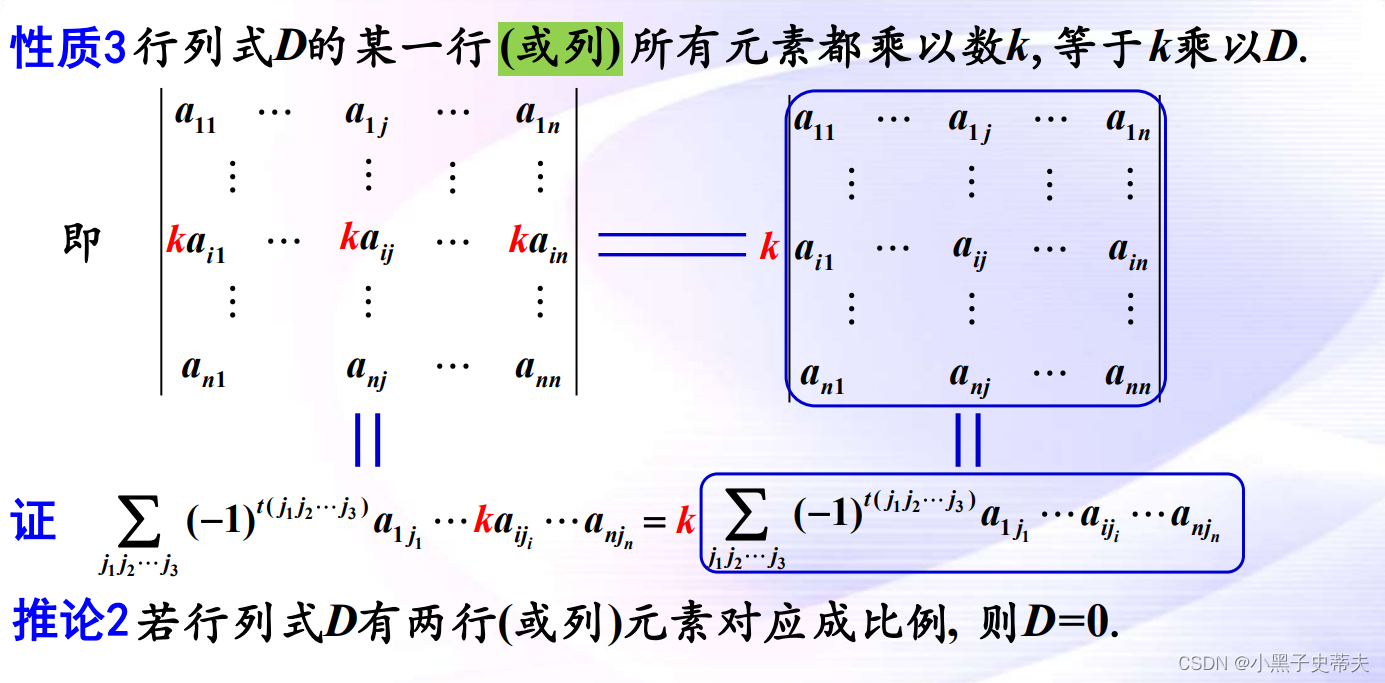
6.4 行列式加法

• 性质4：若行列式D的某列(或行)元素都是两数之和,则D=两行列式之和

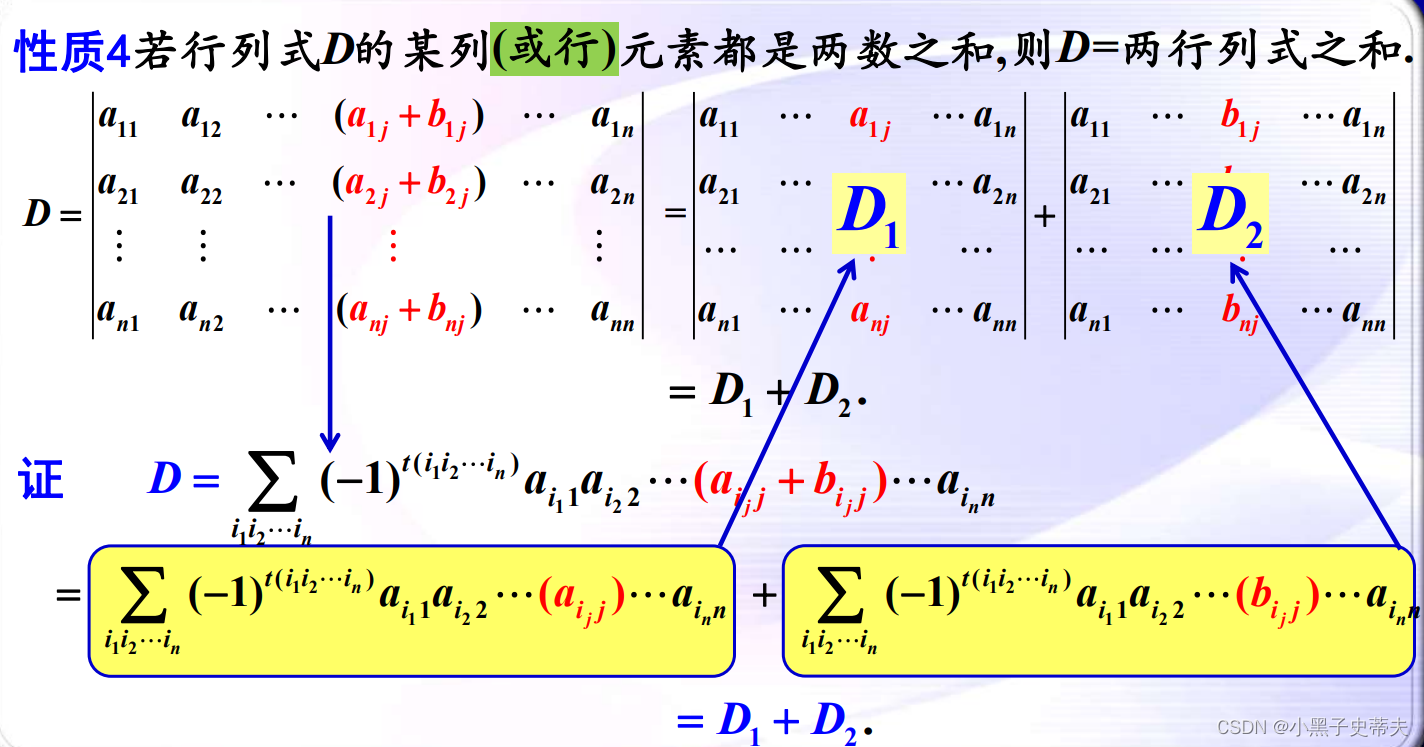
6.5 倍加不变

• 性质5：将行列式D的某一行(或列)上所有的元素都乘以数k，加到另一行(或列)对应的元素上,D的值不变.

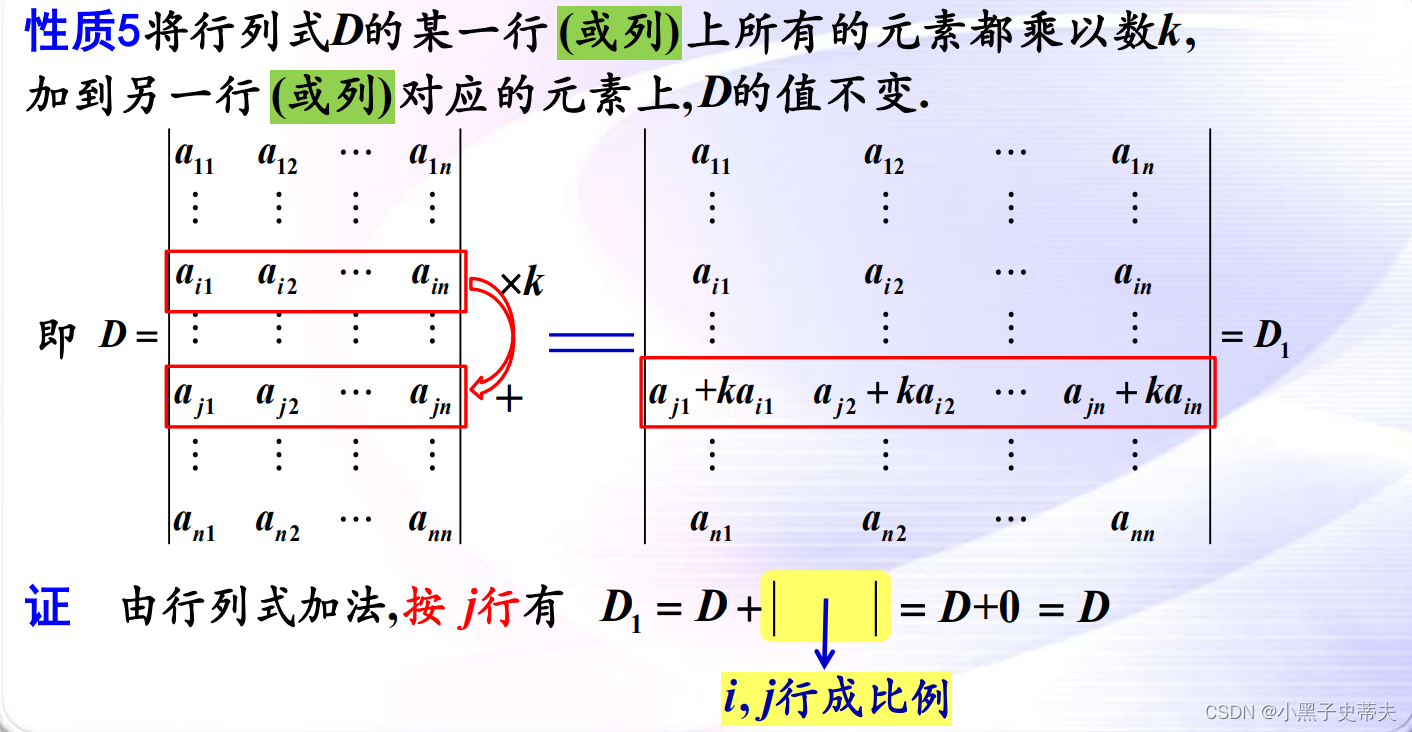
6.6 性质的应用

2.

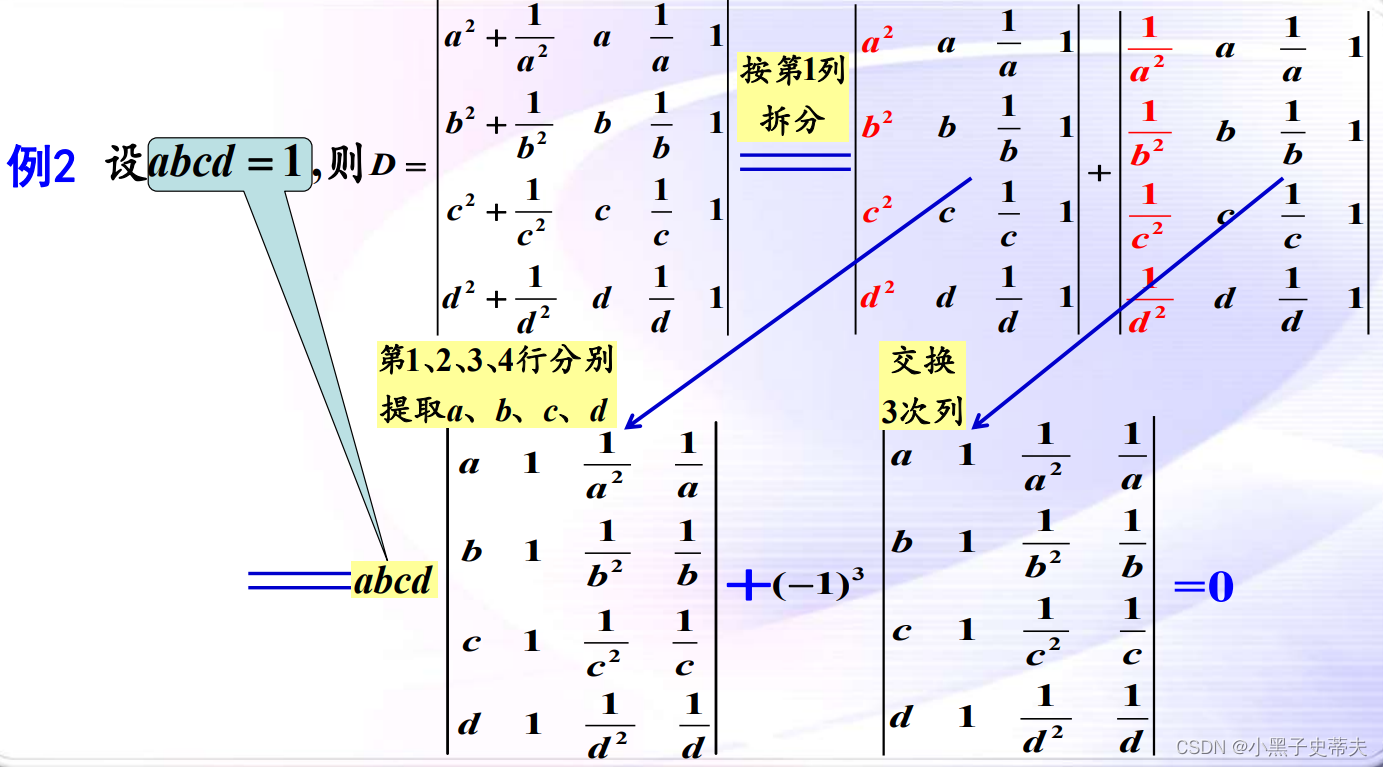
3.

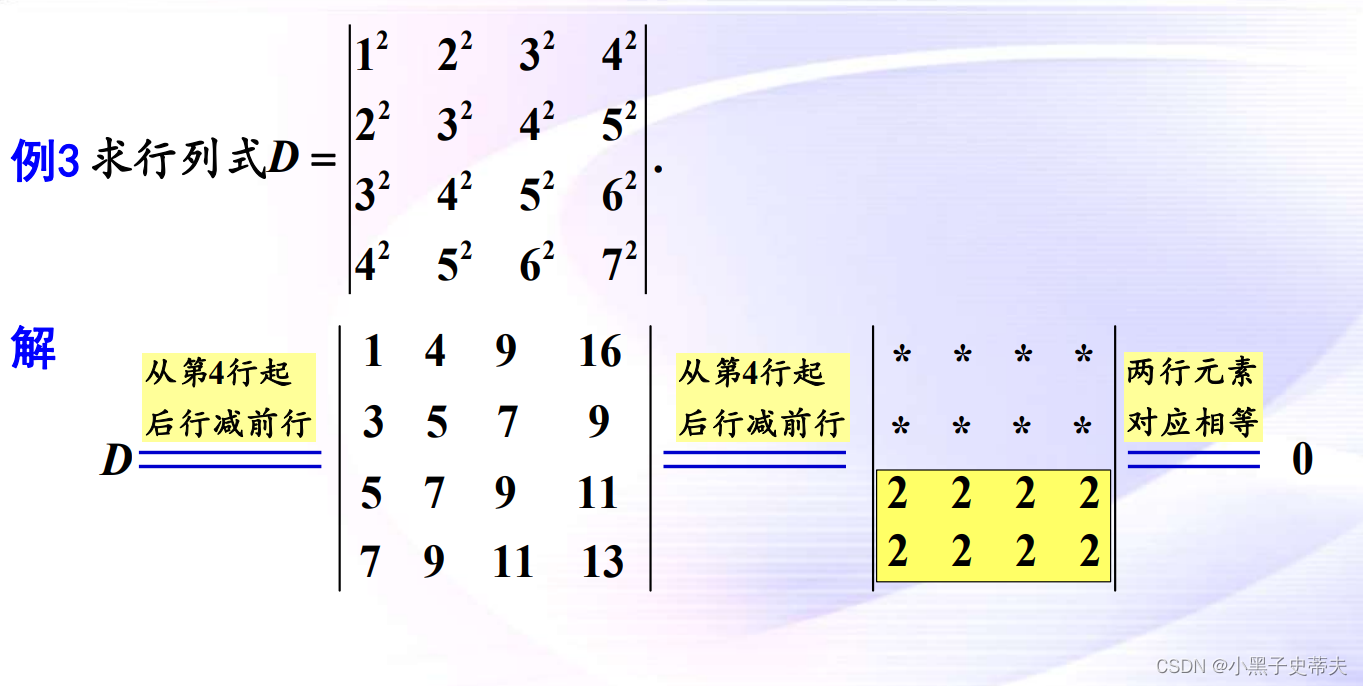
6.7 行列式的初等变换

初等变换的应用：
1.

2.

3.

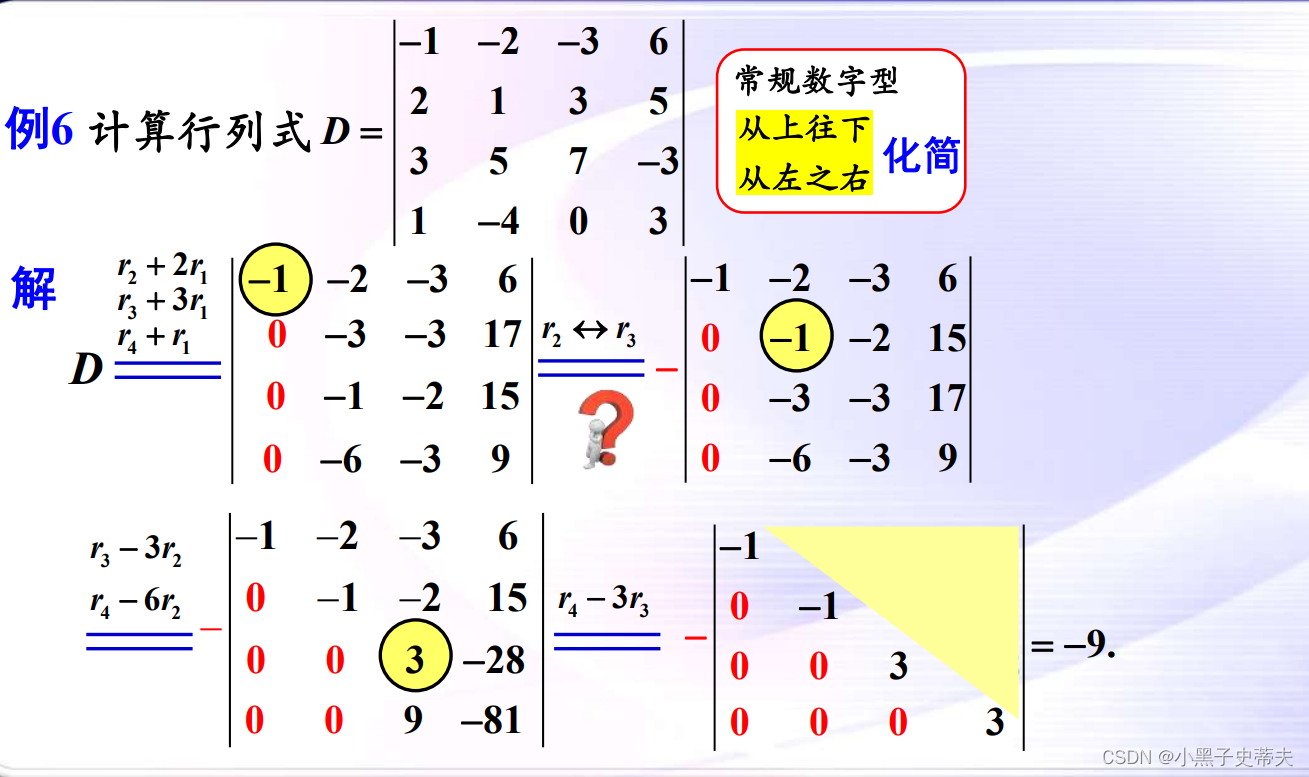
6.8 小结

7. 三阶行列式的展开

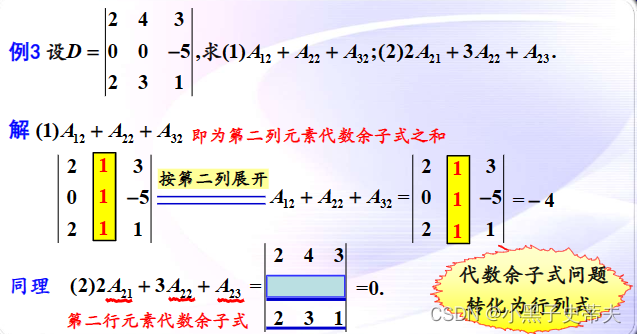
小结：

8. n阶行列式的展开定理

8.1 引理1

8.2 引理2

8.3 定理n阶行列式的值等于它的任一行(或列)的每个元素与其对应代数余子式的乘积之和。

8.4 推论：行列式的某一行(或列)中各元素与另一行(或列)中对应元素代数余子式的乘积之和等于零。

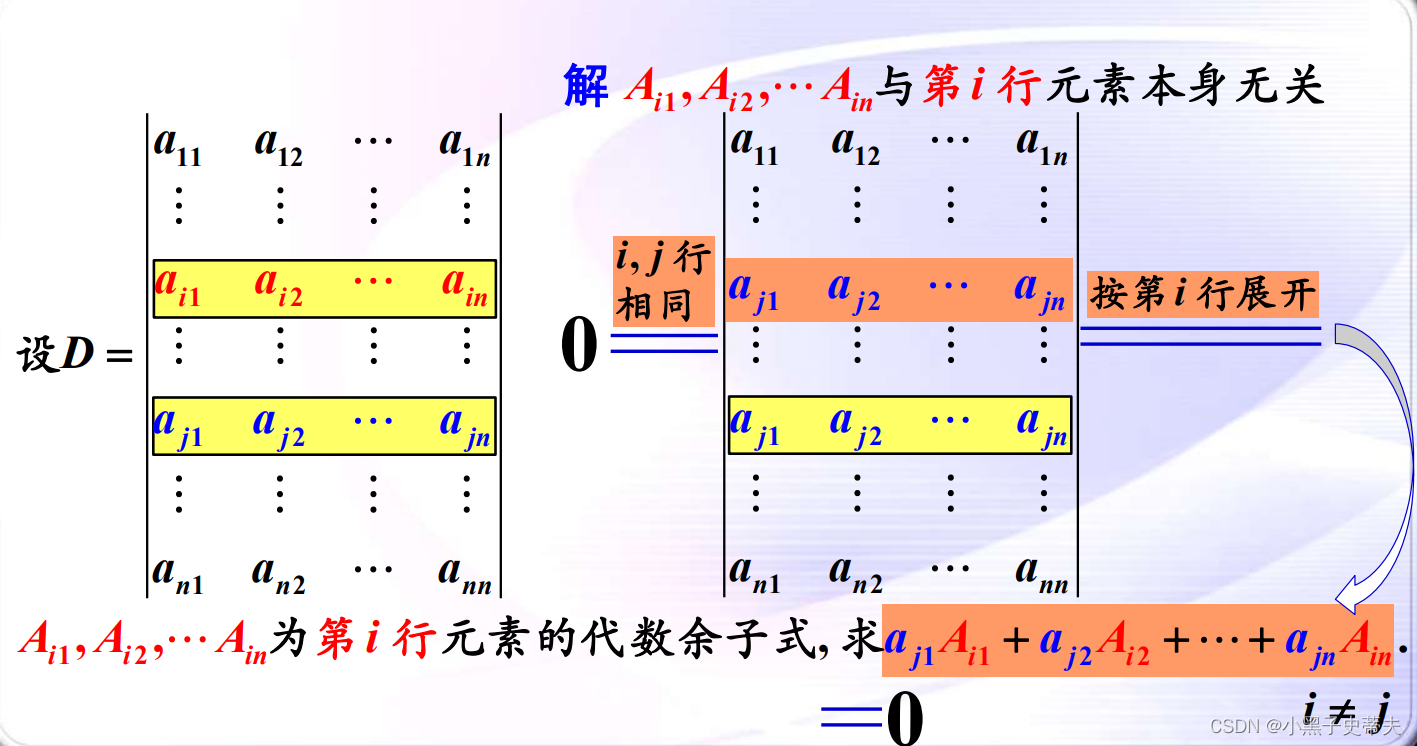
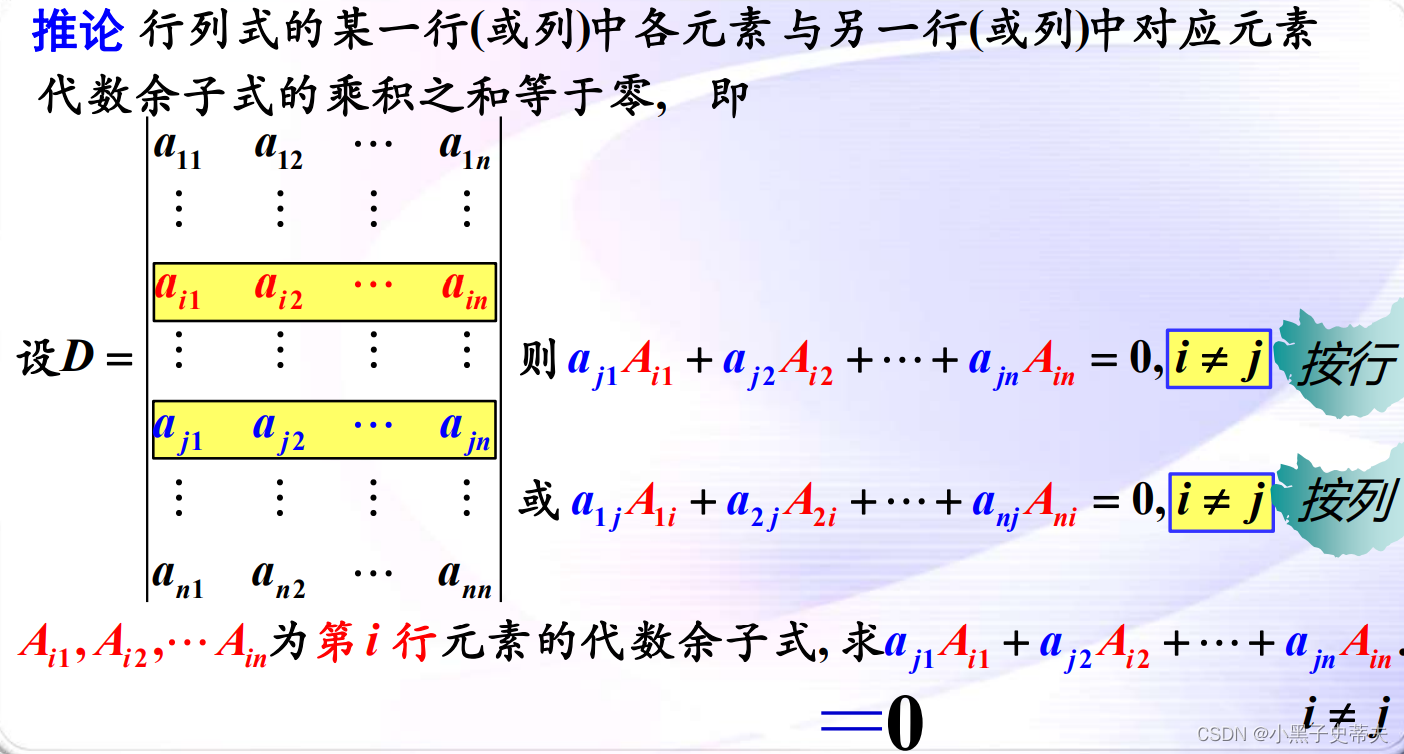
案例：

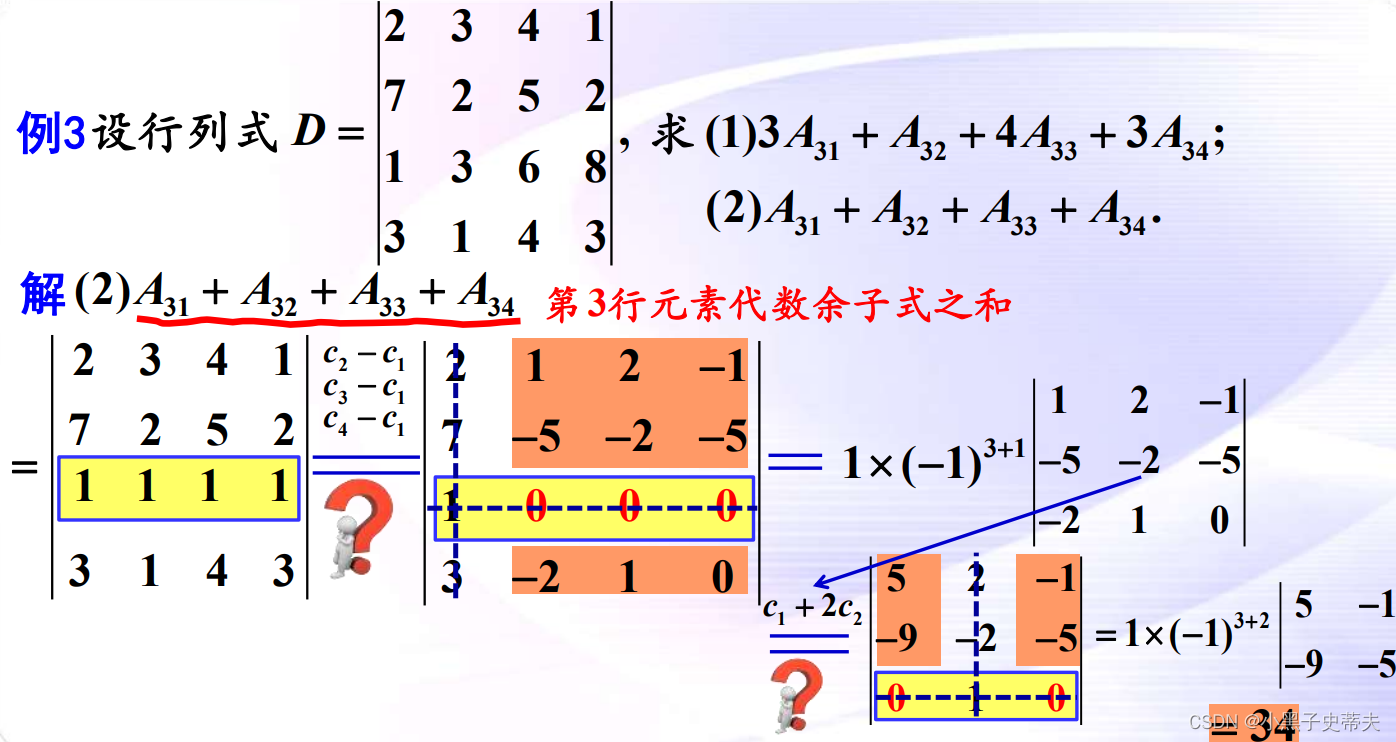
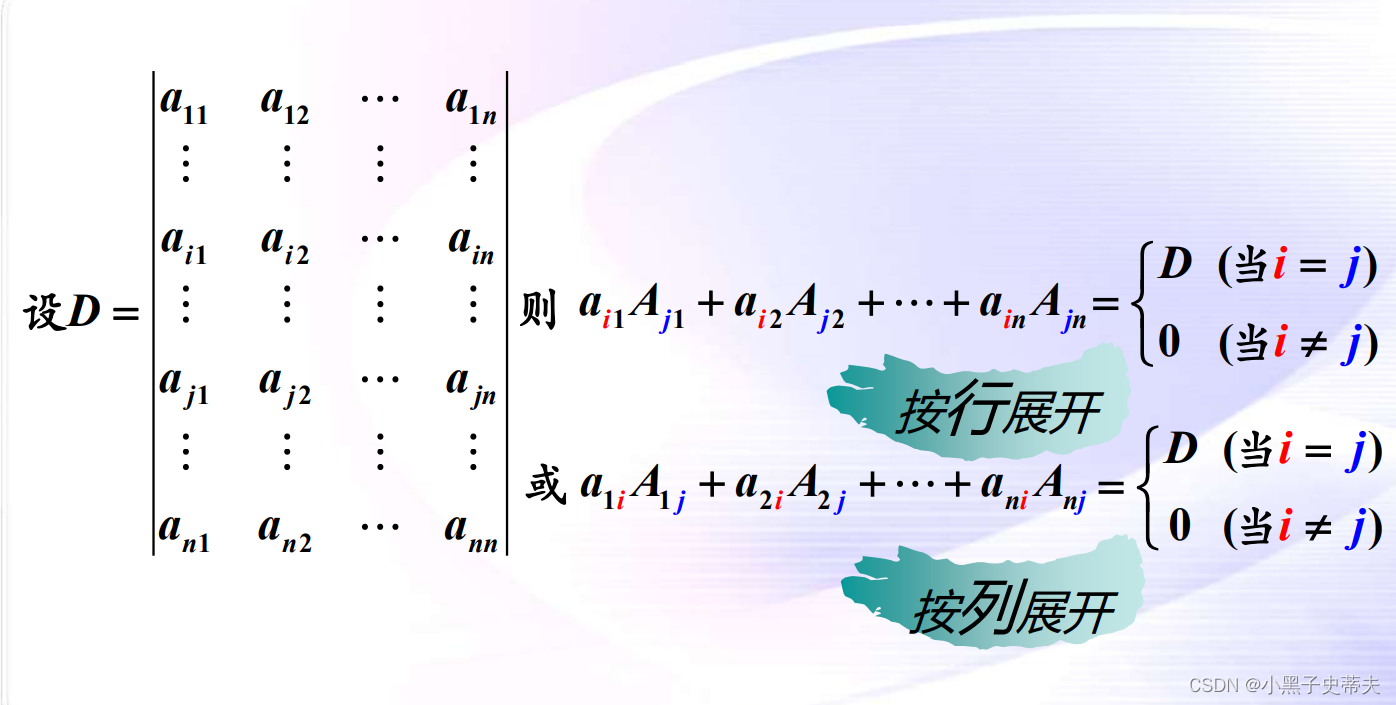
8.5 小结：

9. 行列式的计算

9.1 行列式常用方法

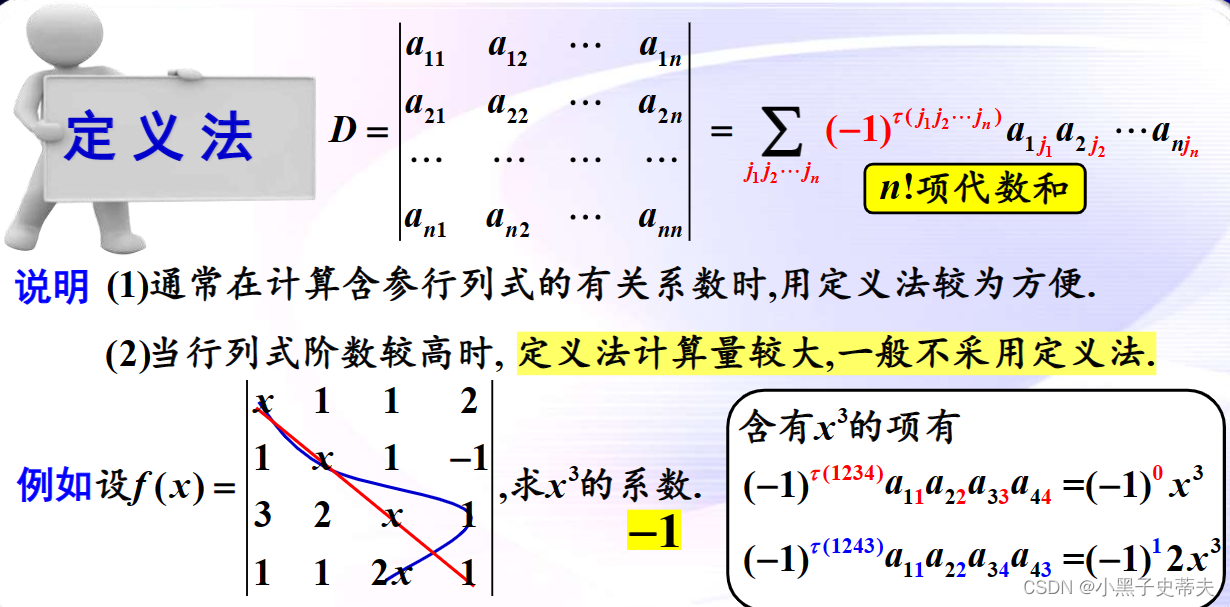
2.

3.

4.

行列式的常见类型

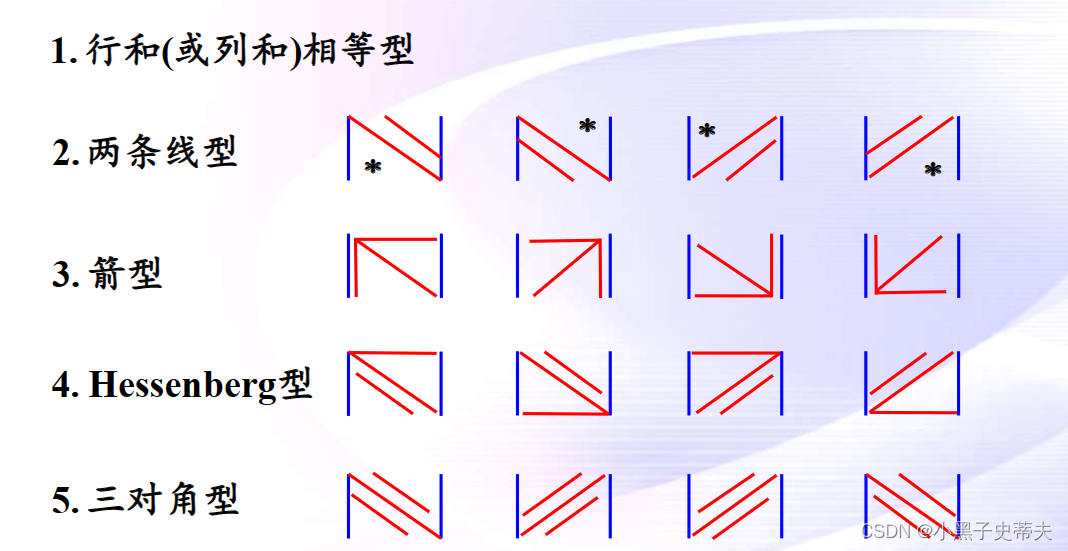
9.1 三角型行列式

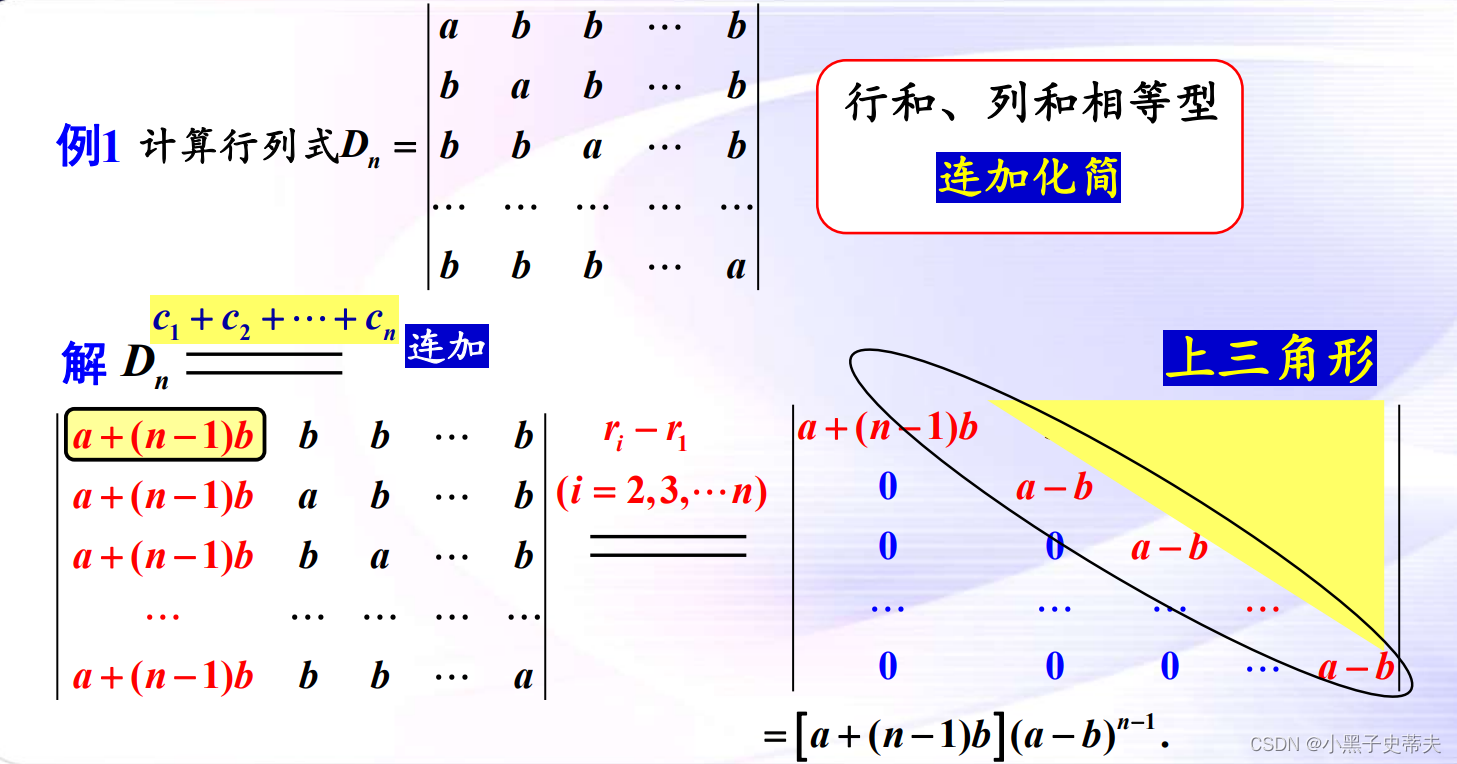
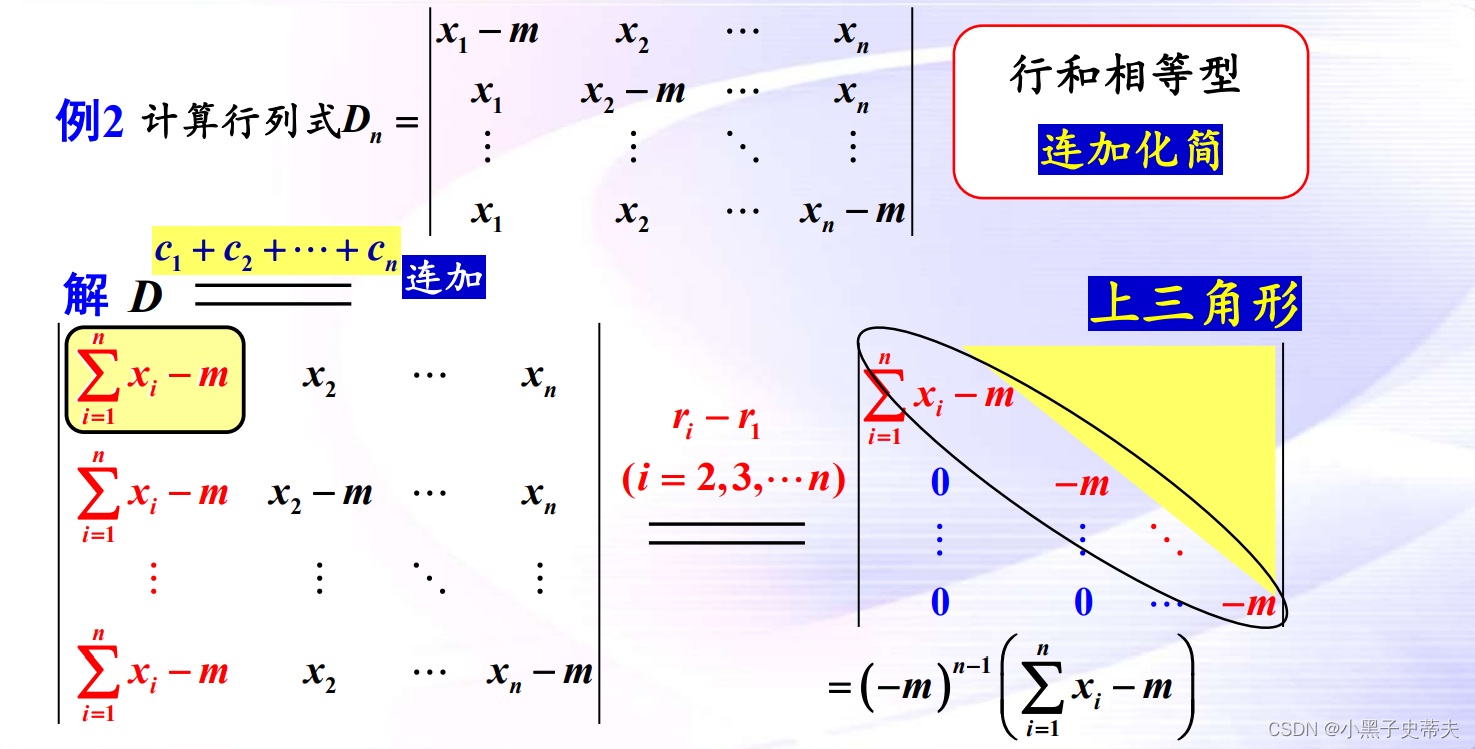
9.2 行和（列和）相等行列式

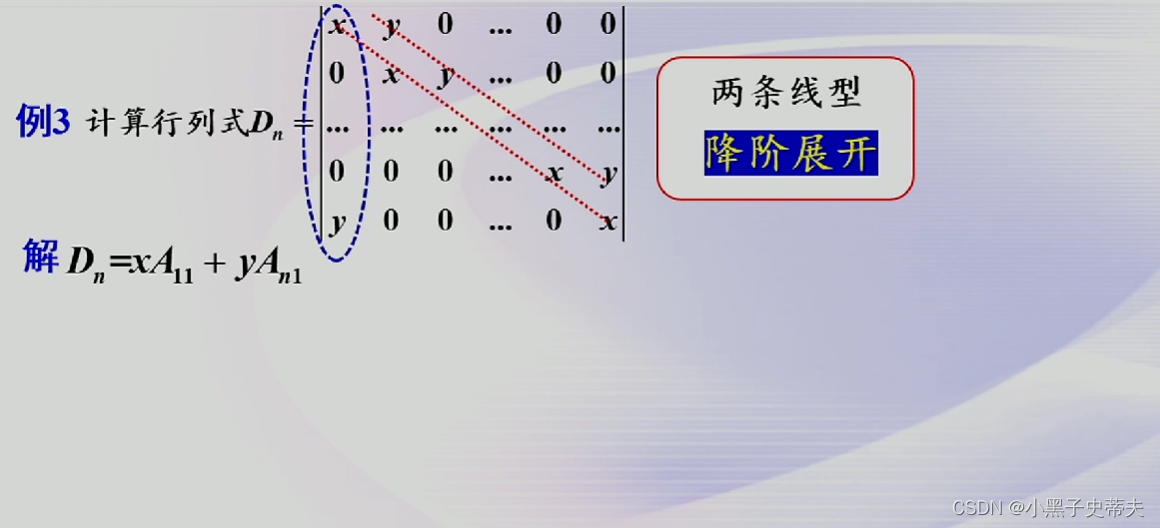
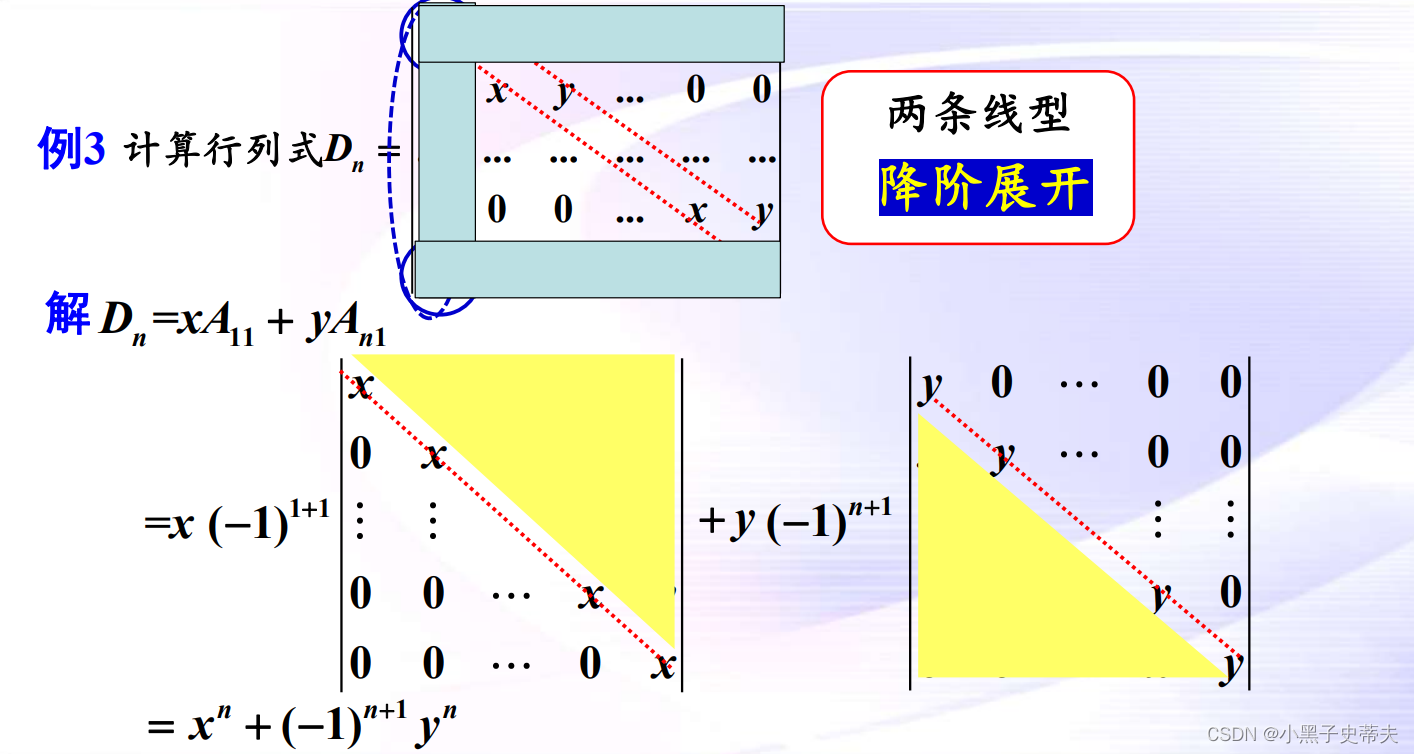
9.3 两条线型行列式

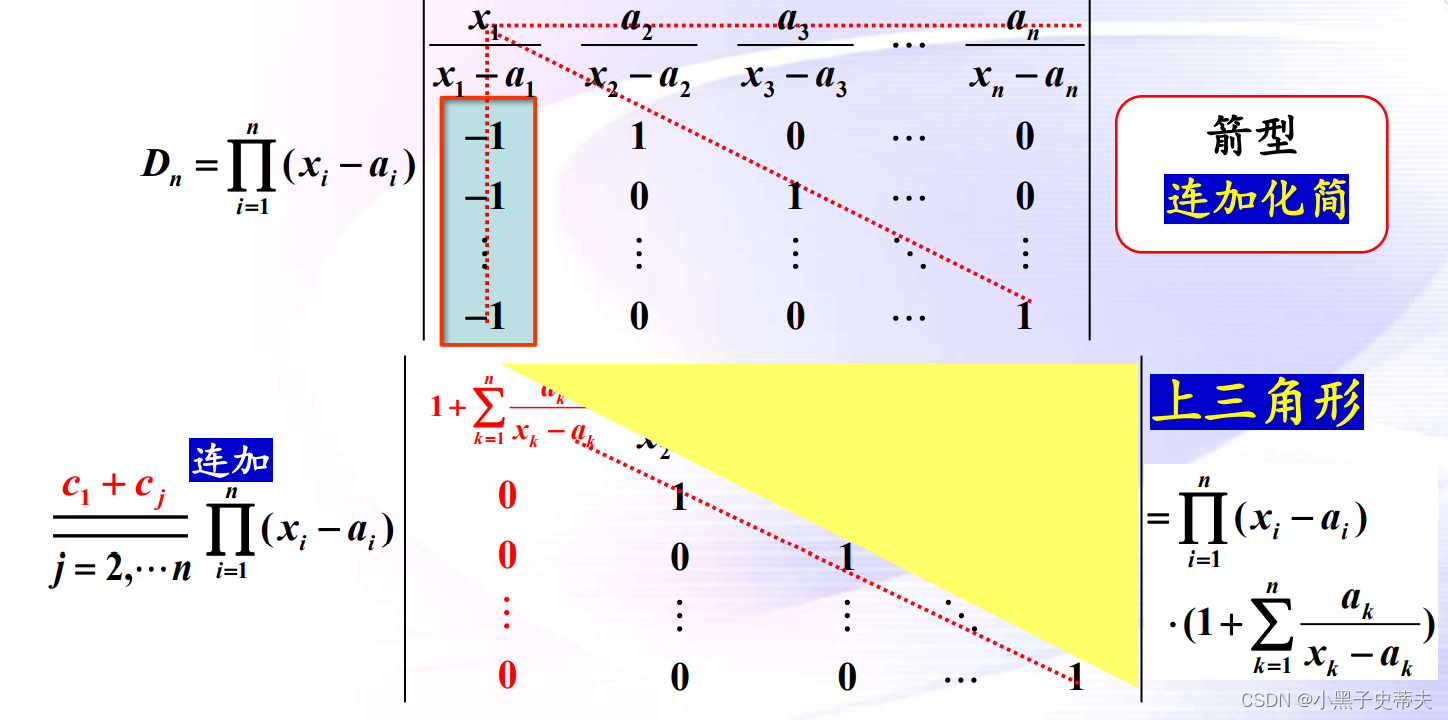
9.4 箭型行列式

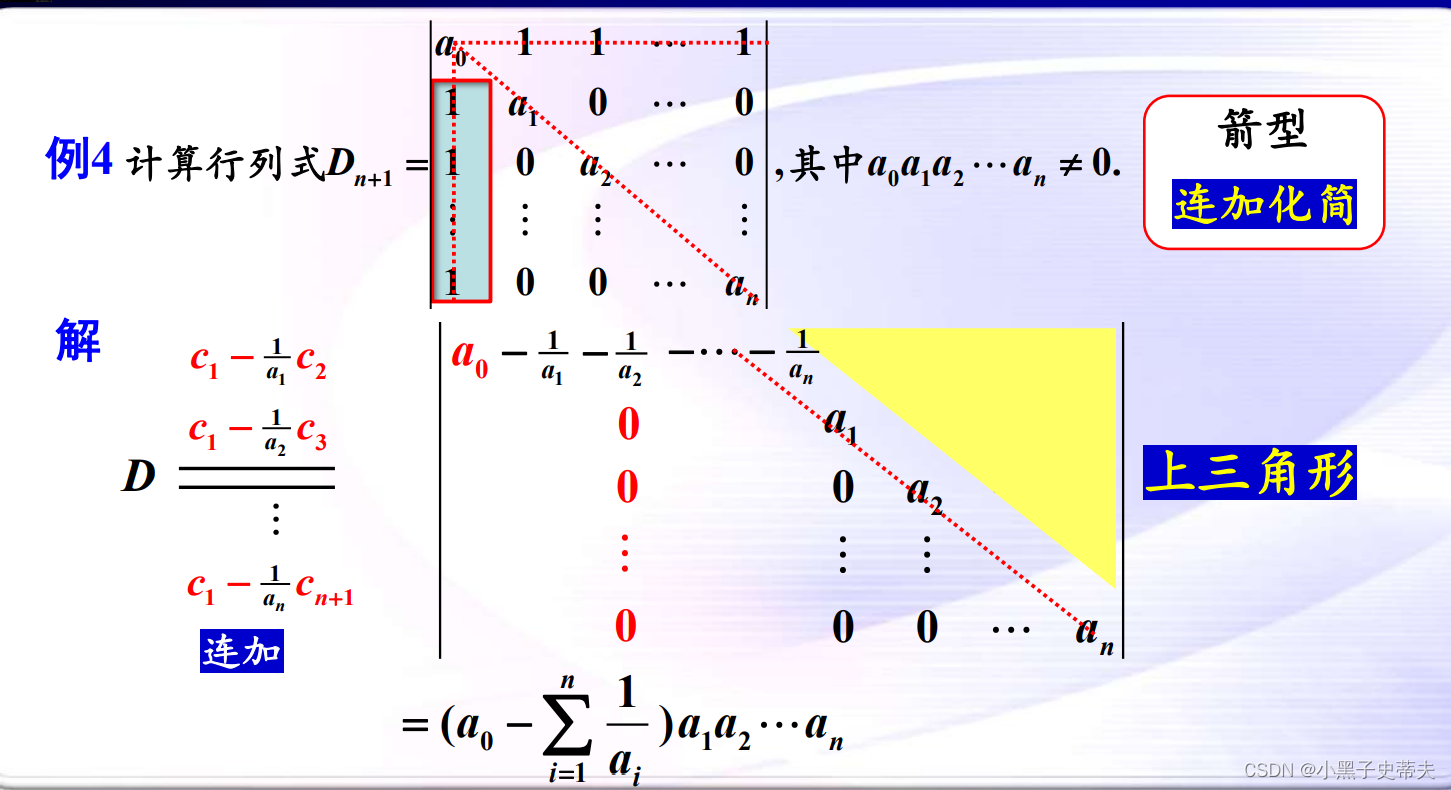
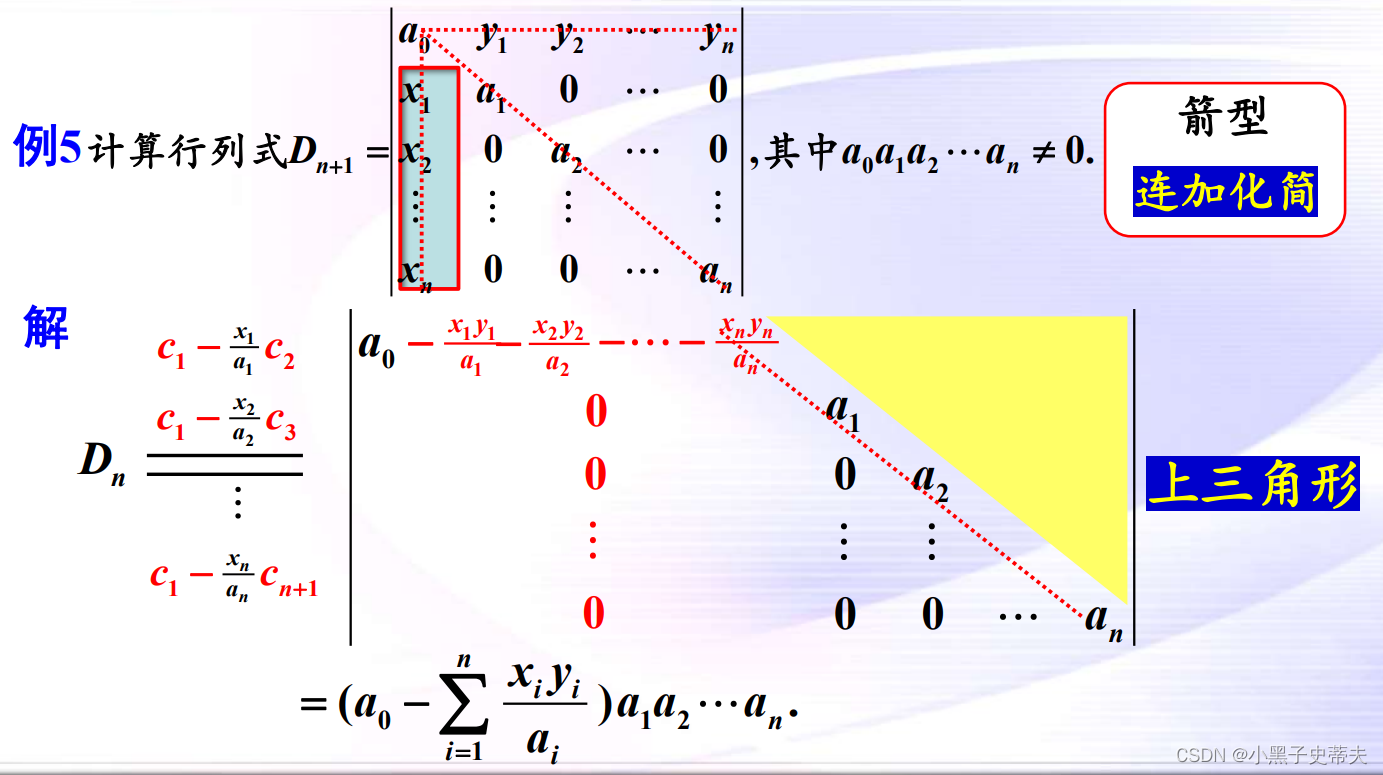
案例：

9.5 拉普拉斯行列式

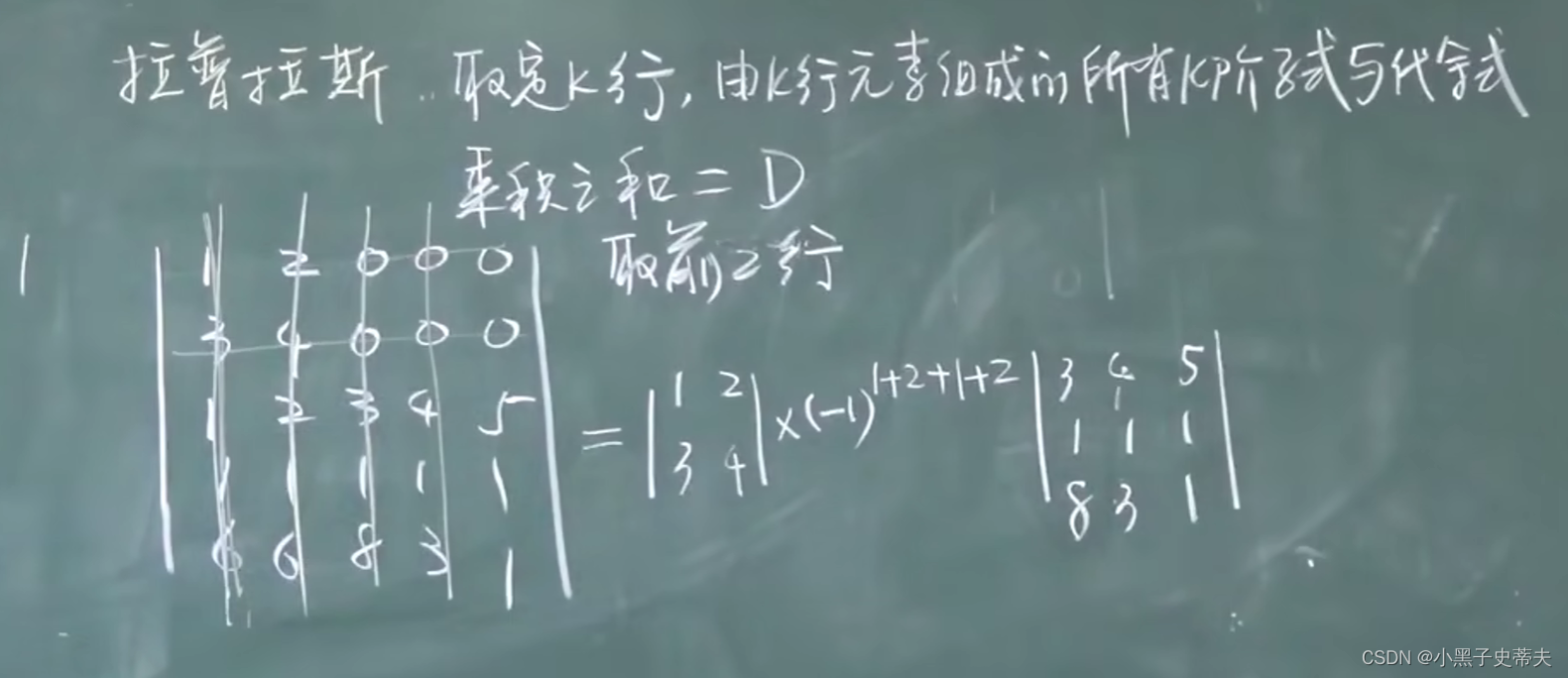
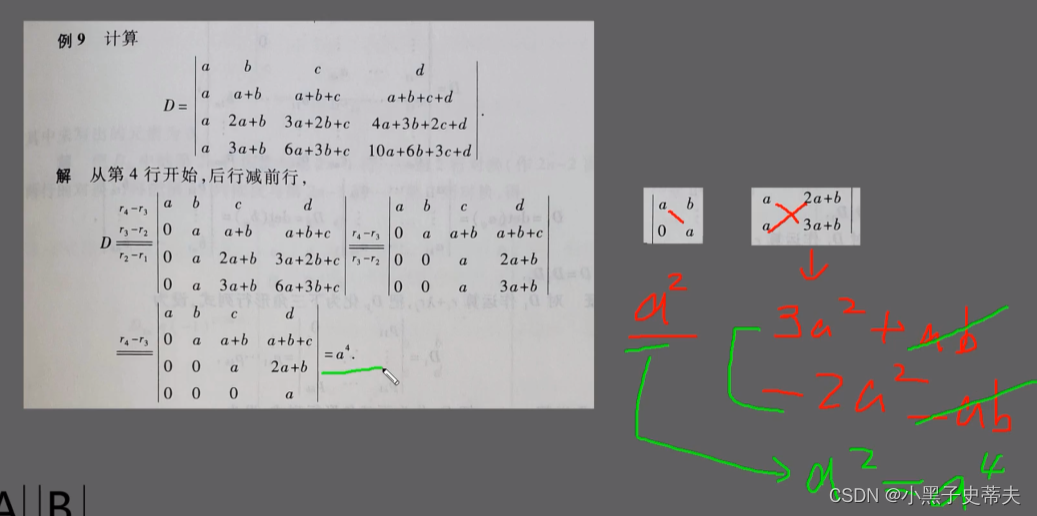
9.6 Hessenberg型行列式

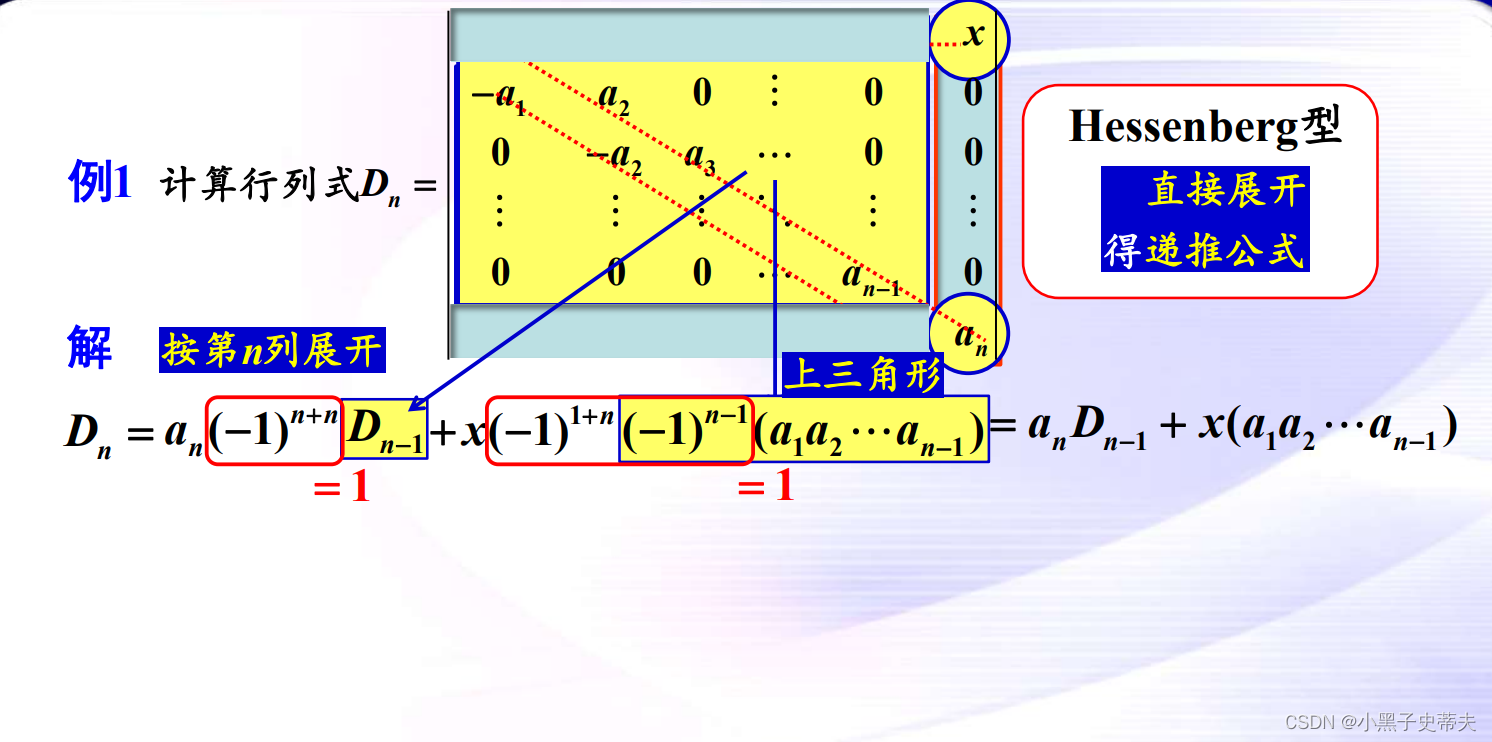
案例：

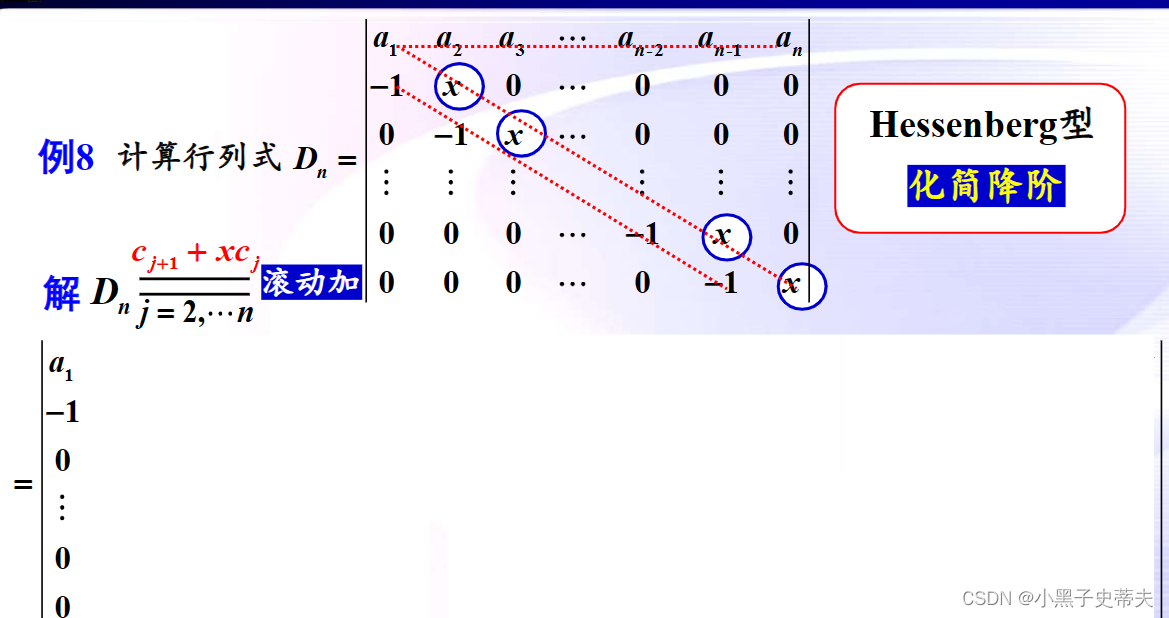
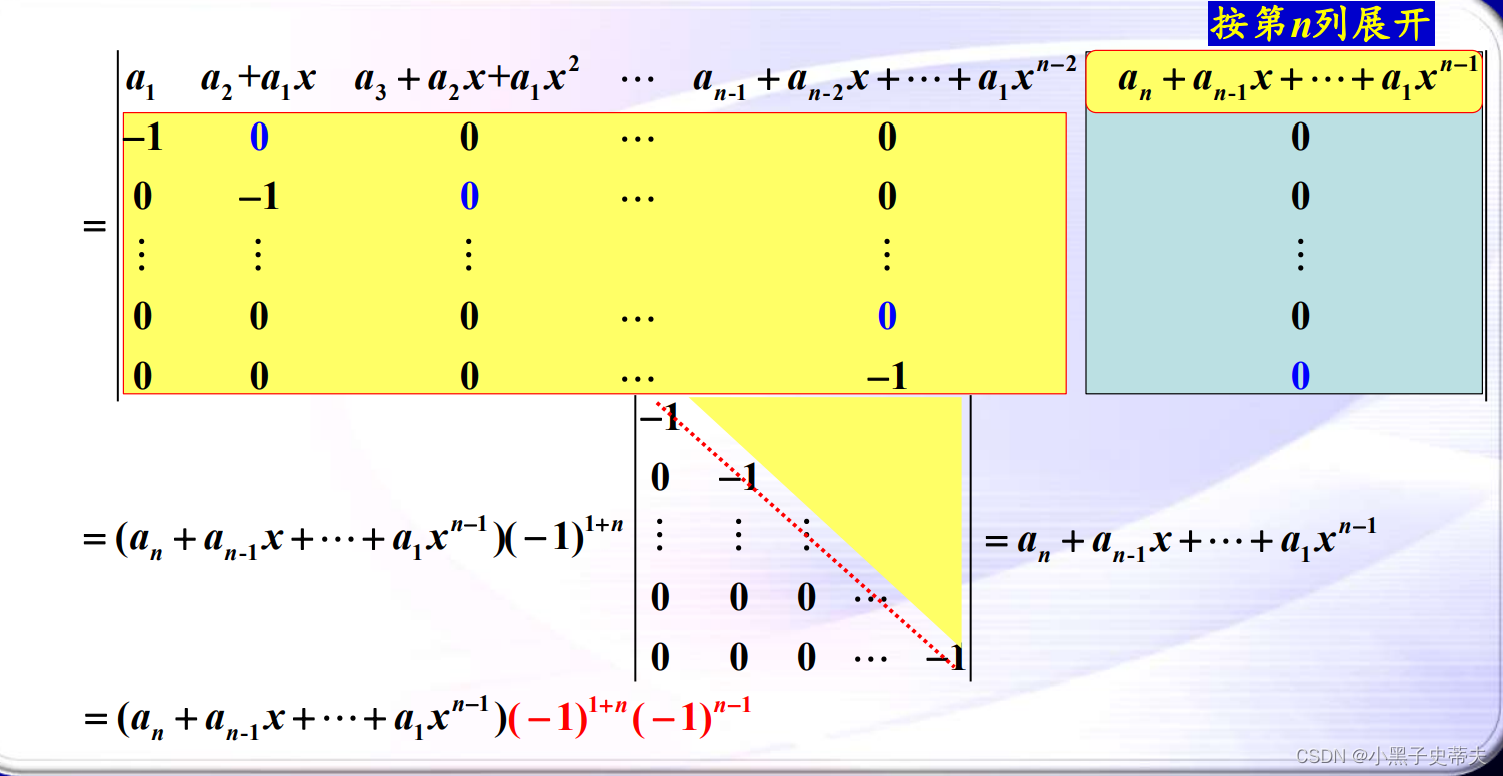
9.7 三对角型（三条线型行列式）

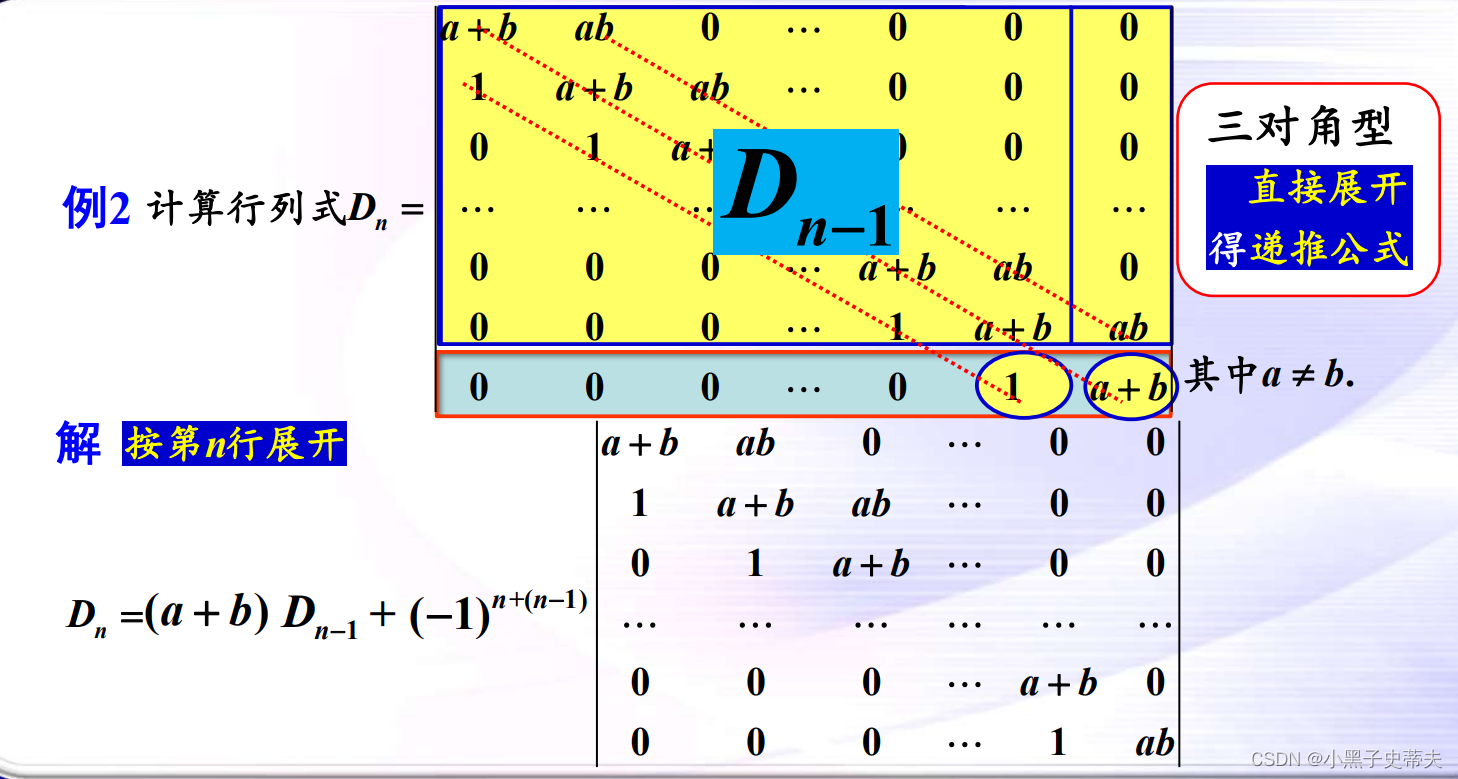
案例：

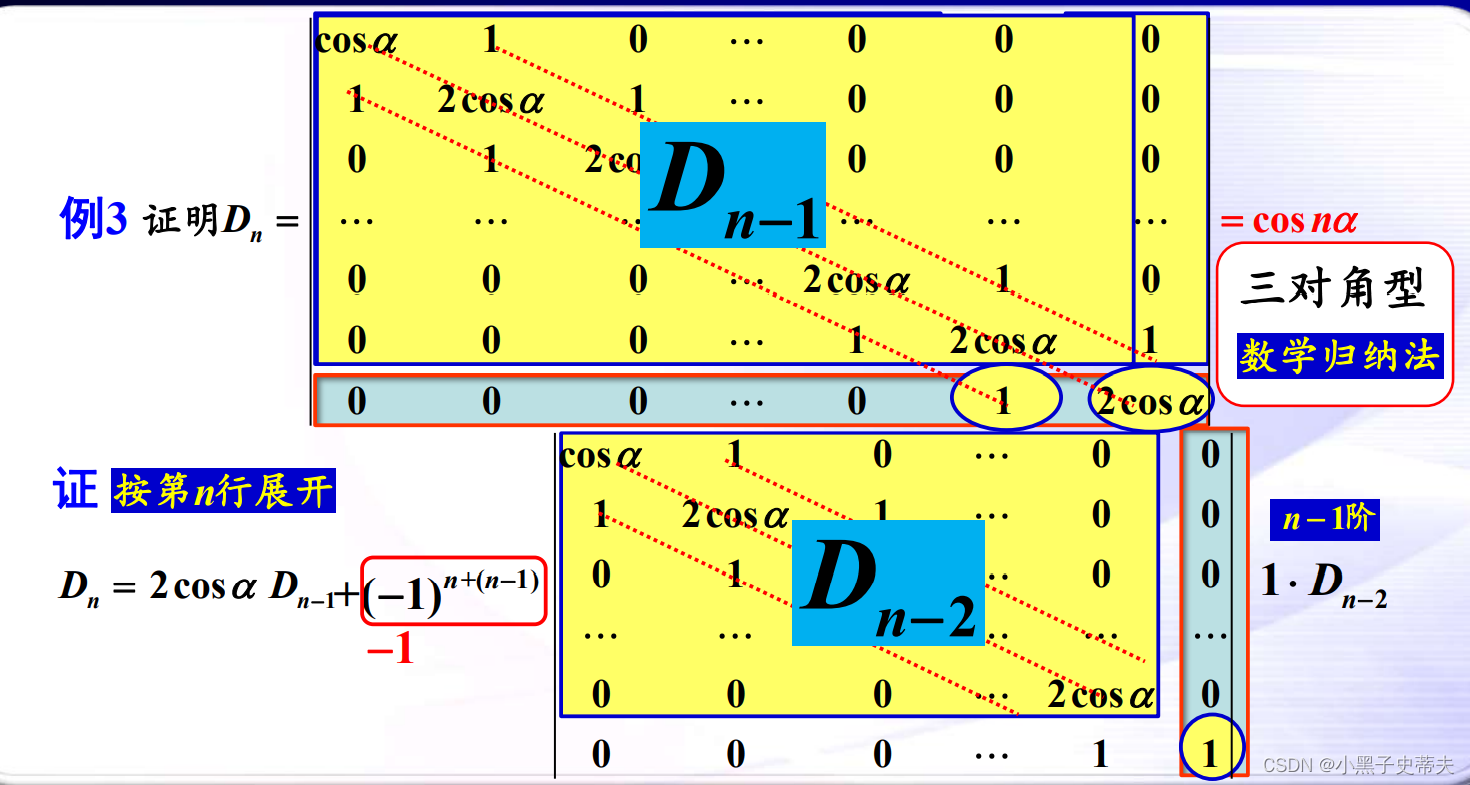
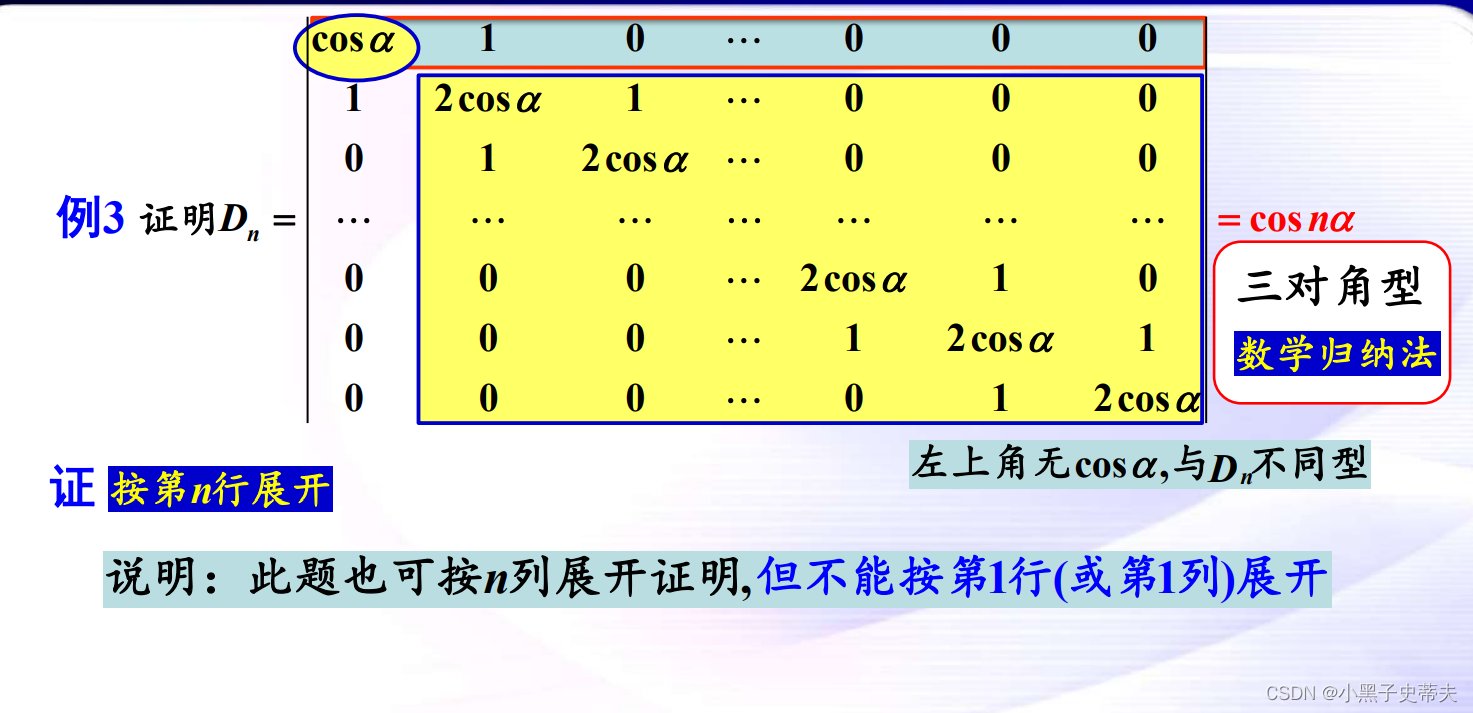
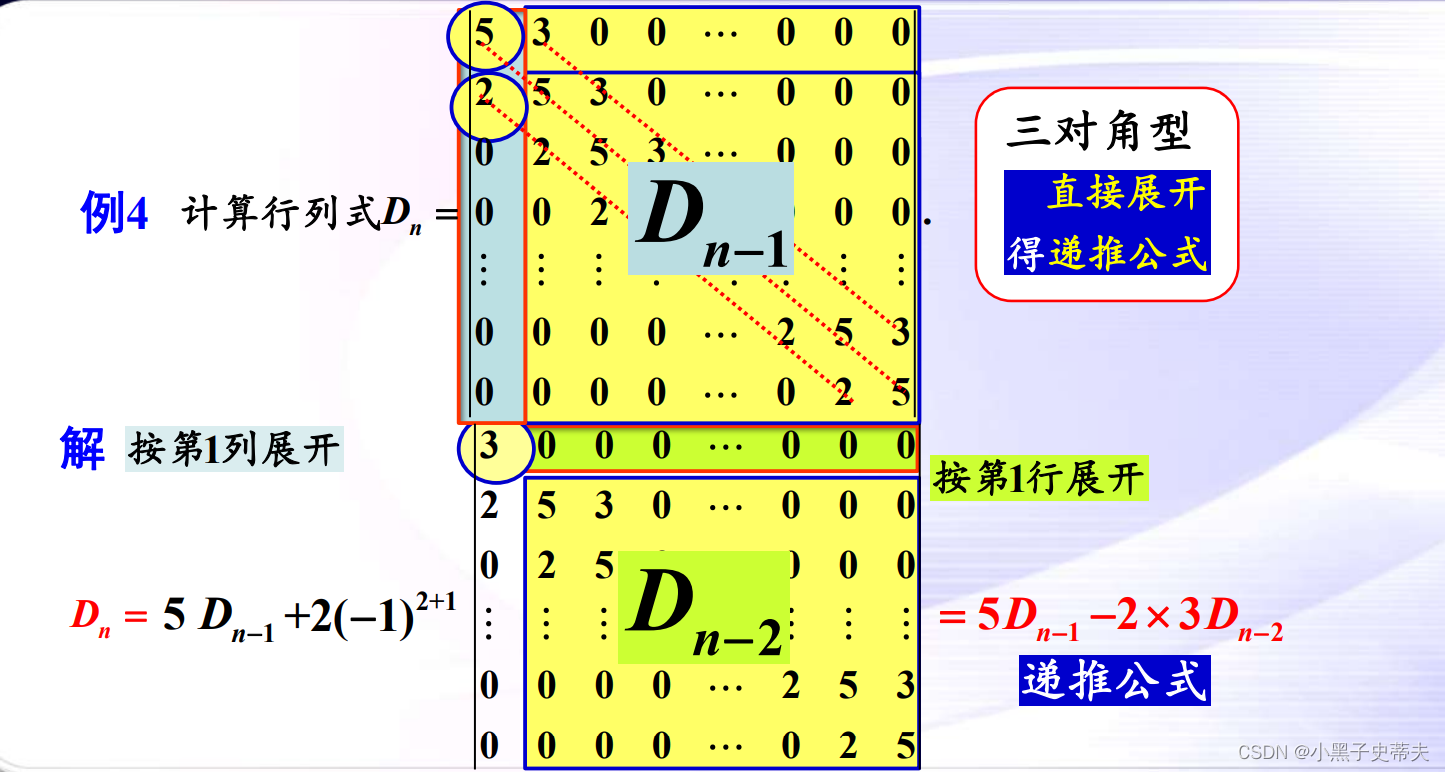
9.8 范德蒙行列式

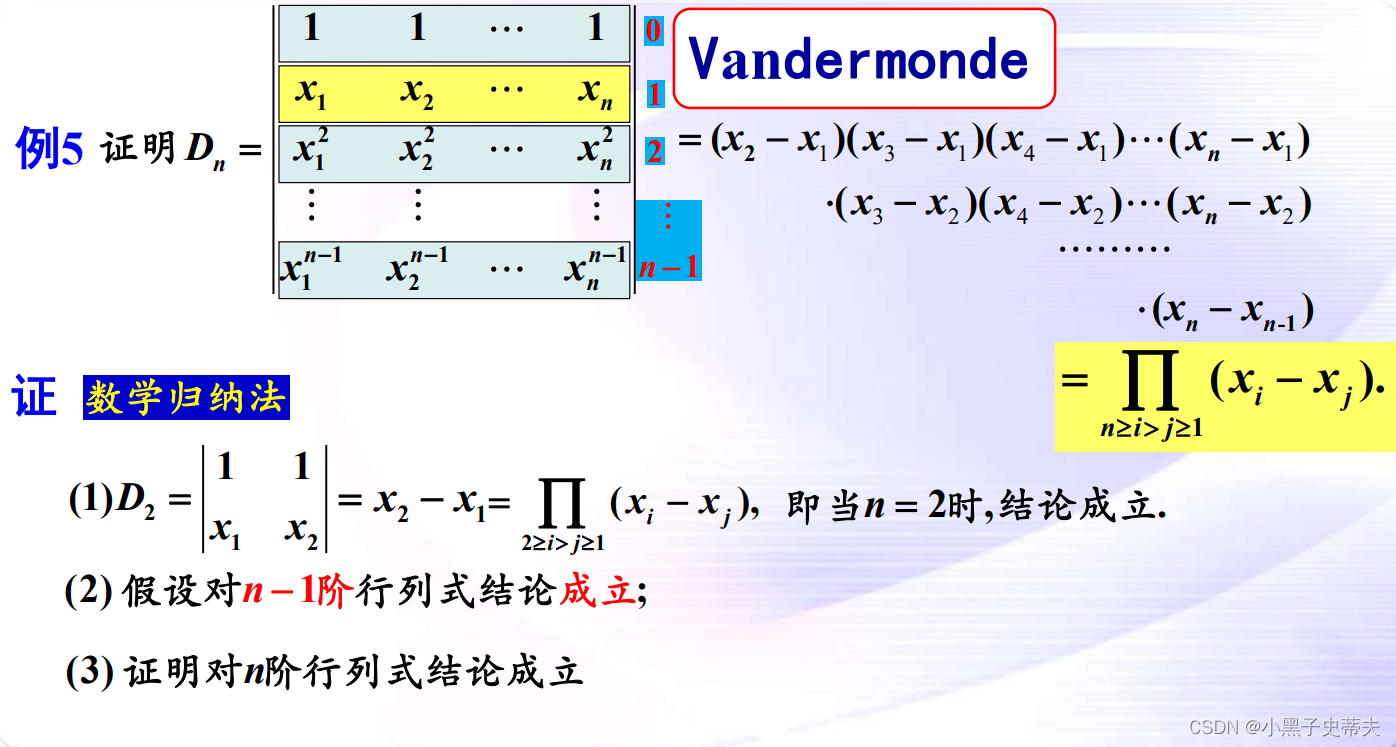
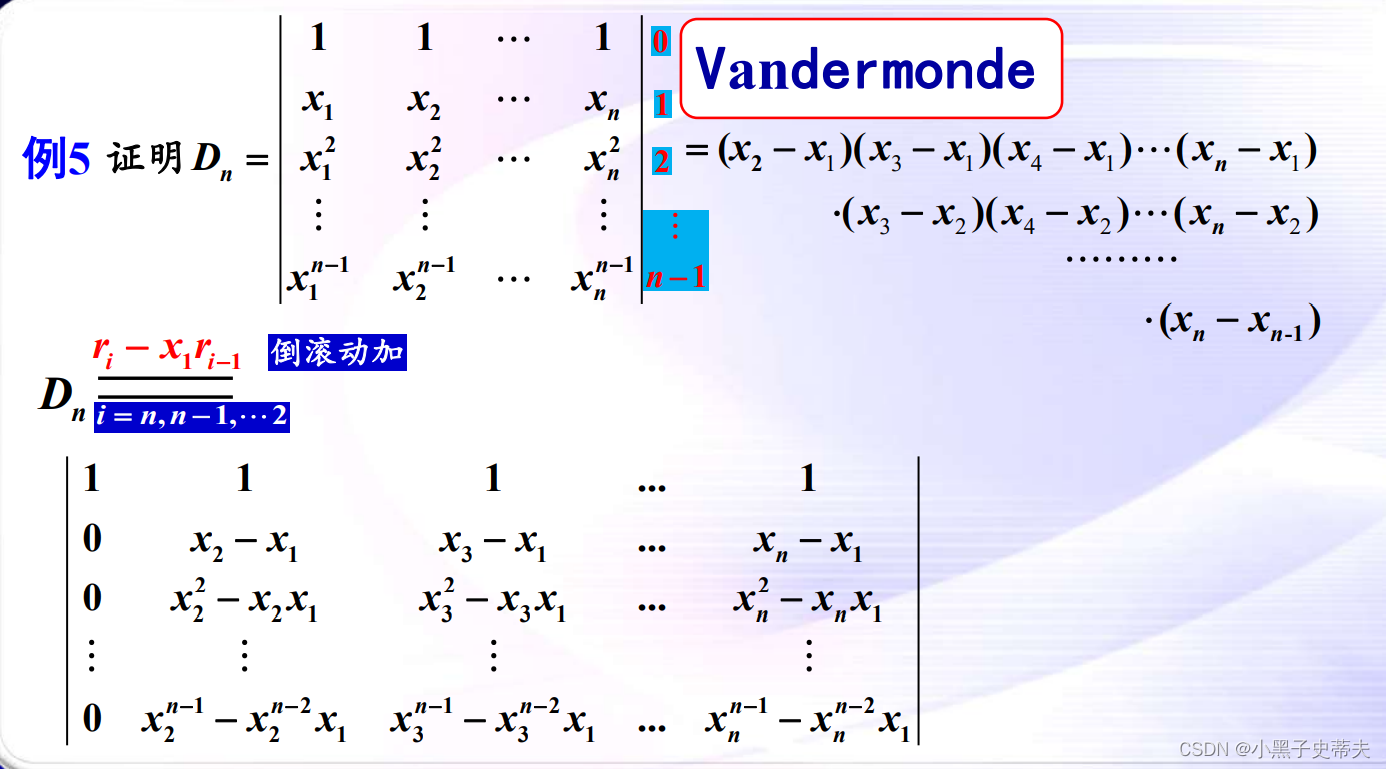
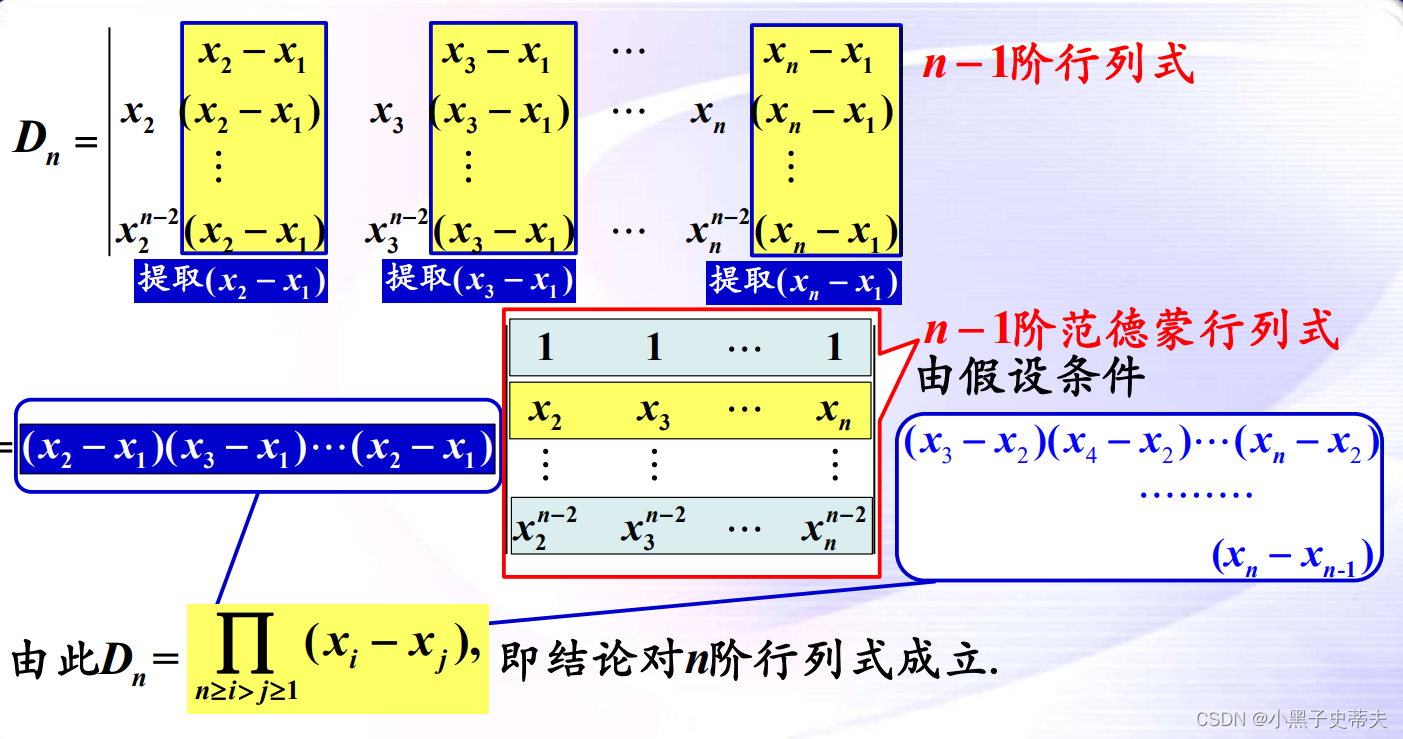
应用

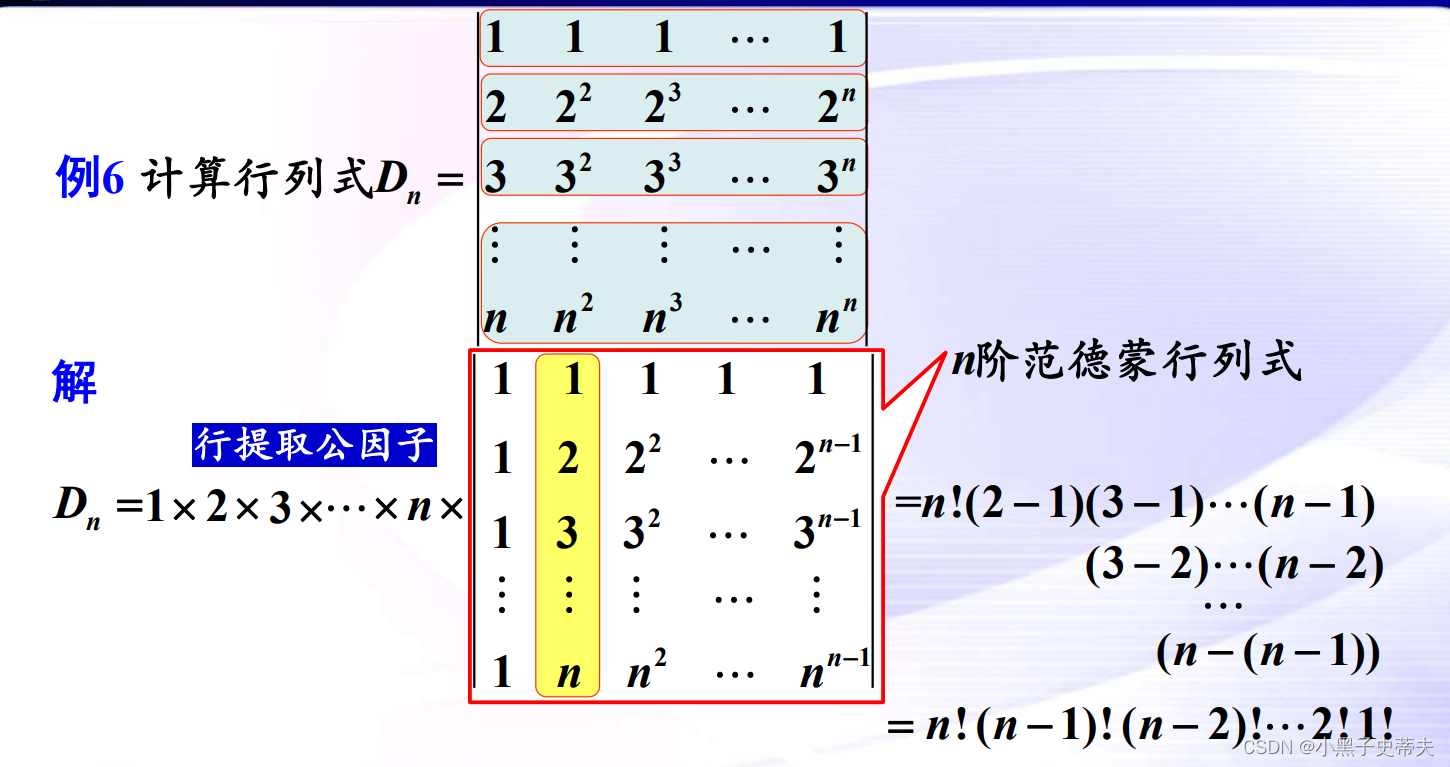
9.9 反对称行列式

奇数反对称行列式（特殊）

9.10 对称行列式

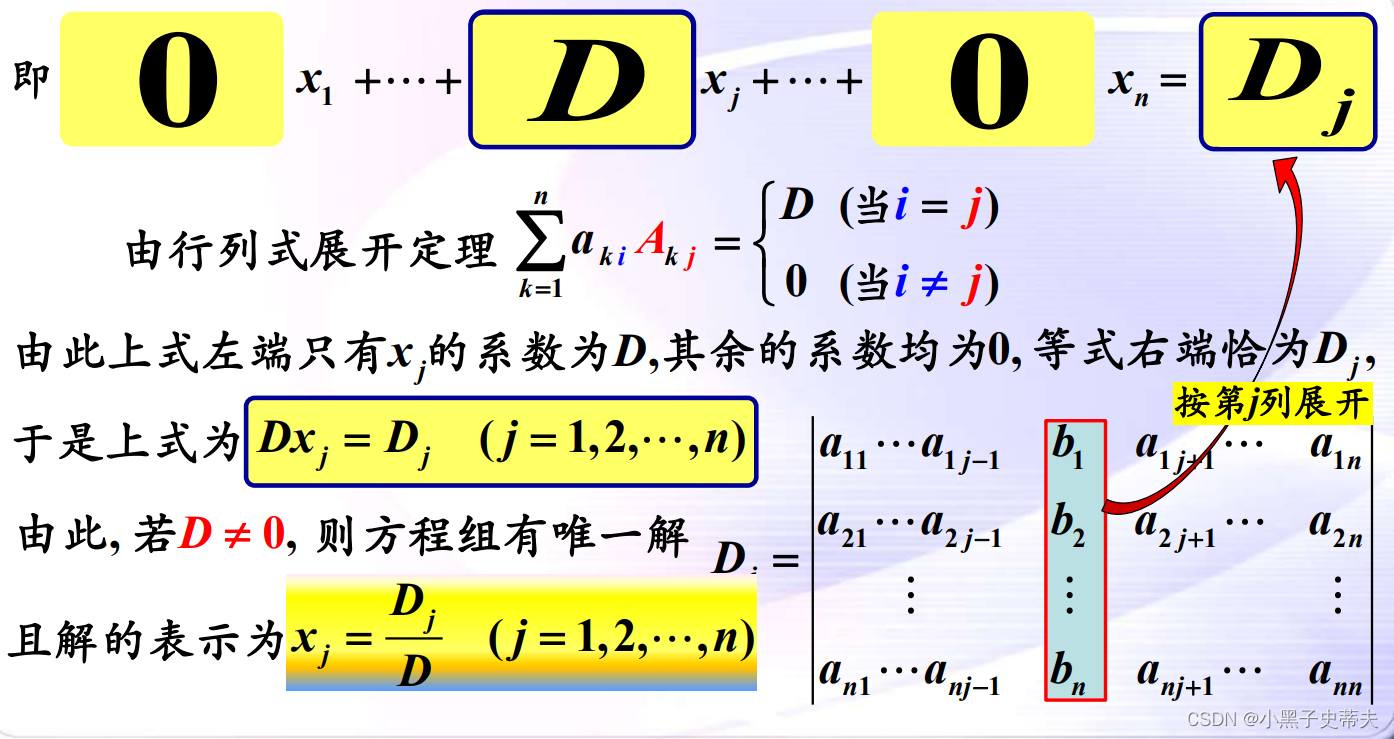
10. 克莱姆法则

引导：

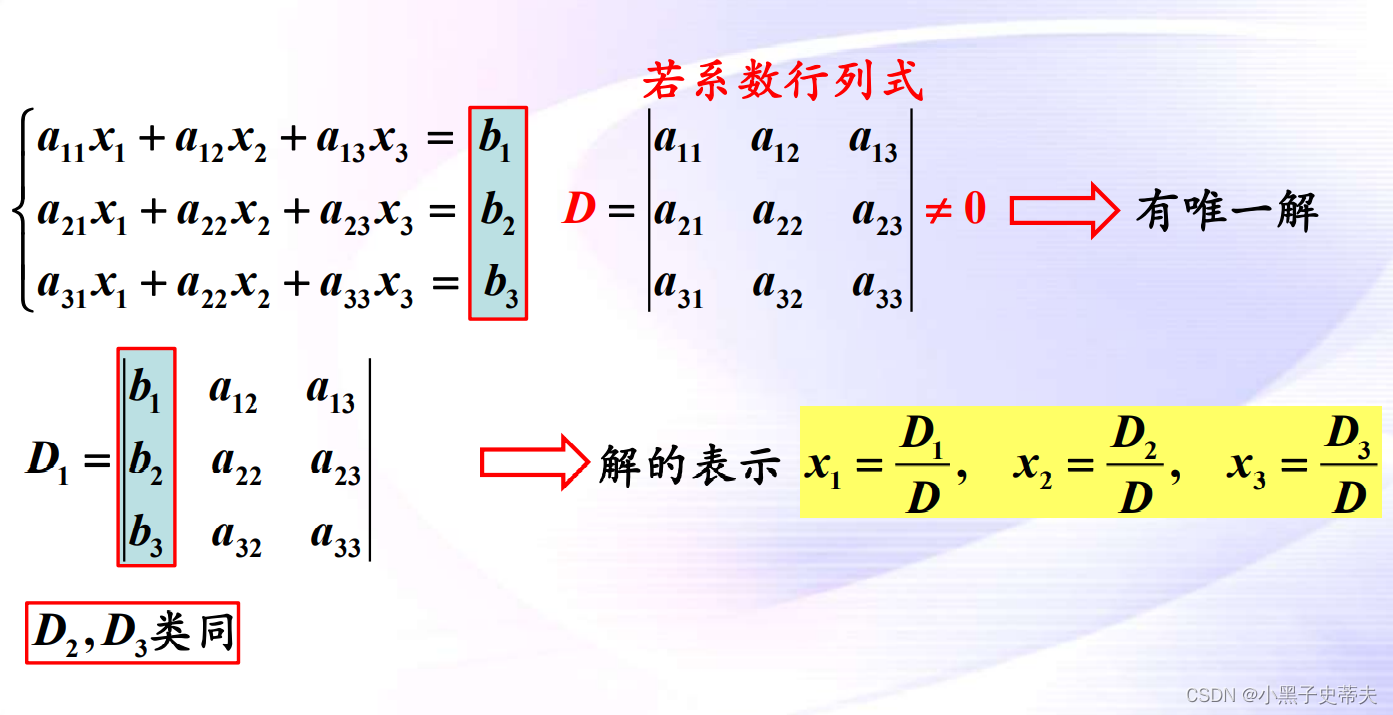
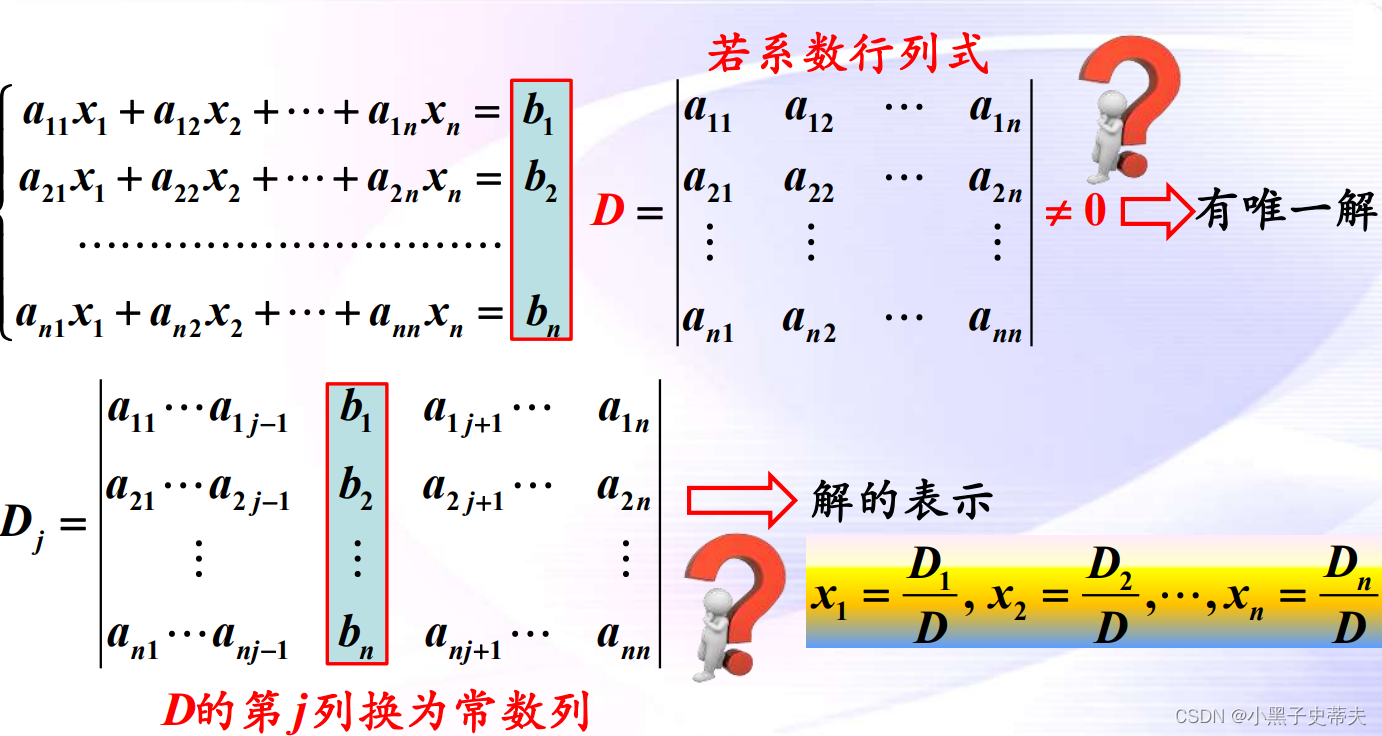
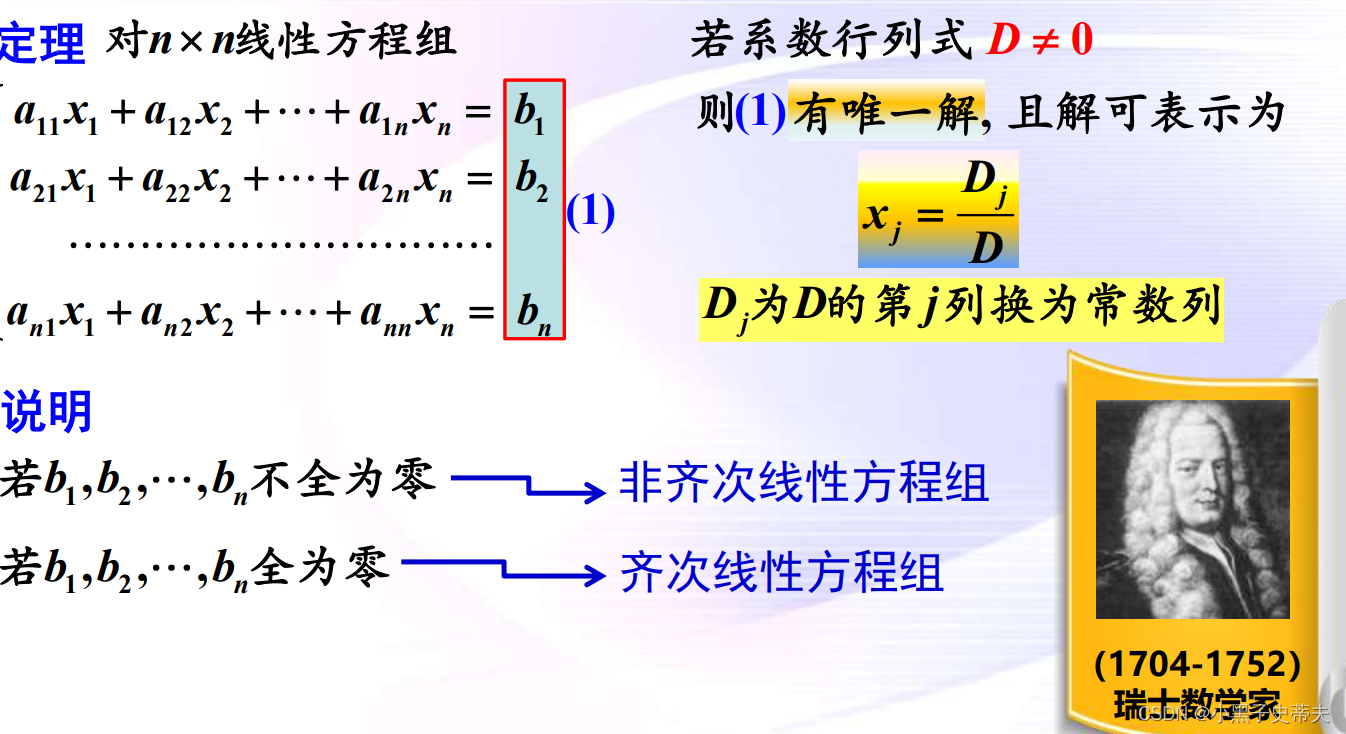
10.1 非齐次线性方程组

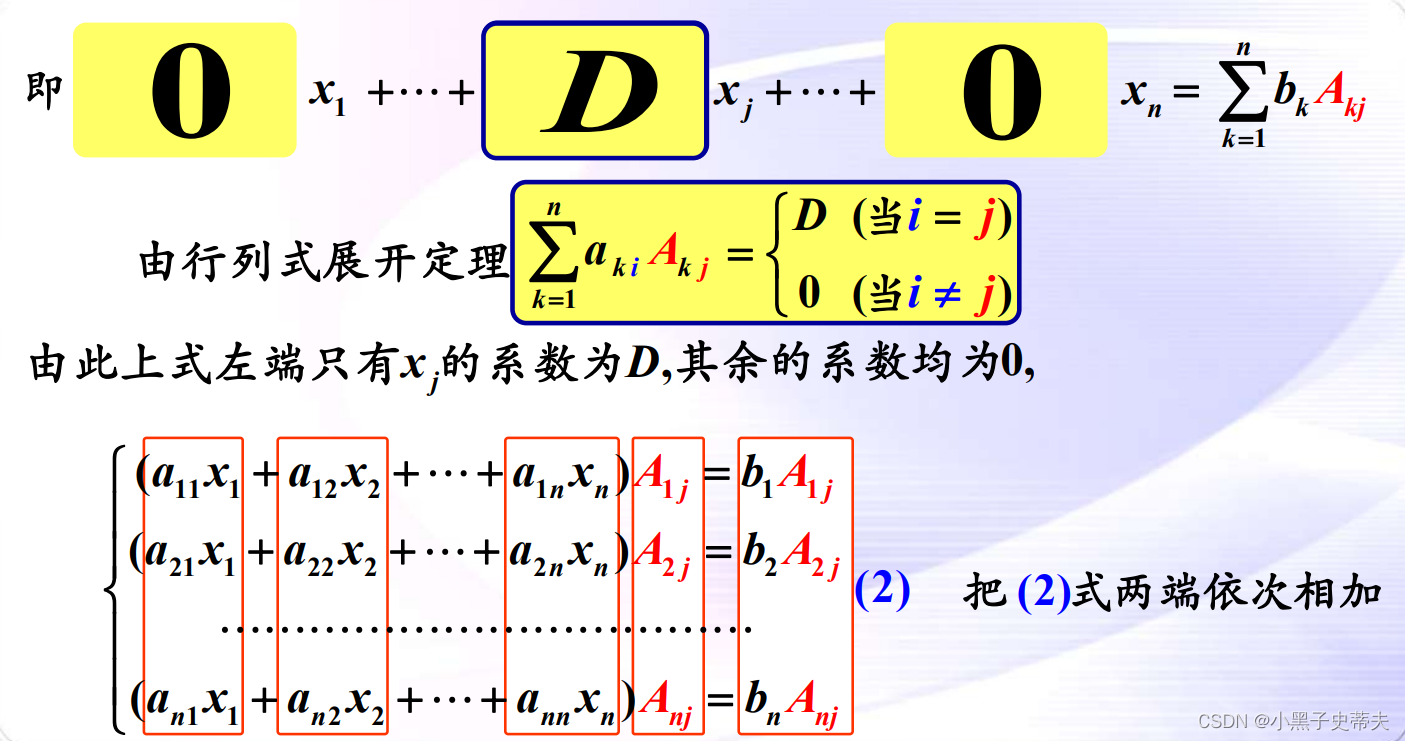
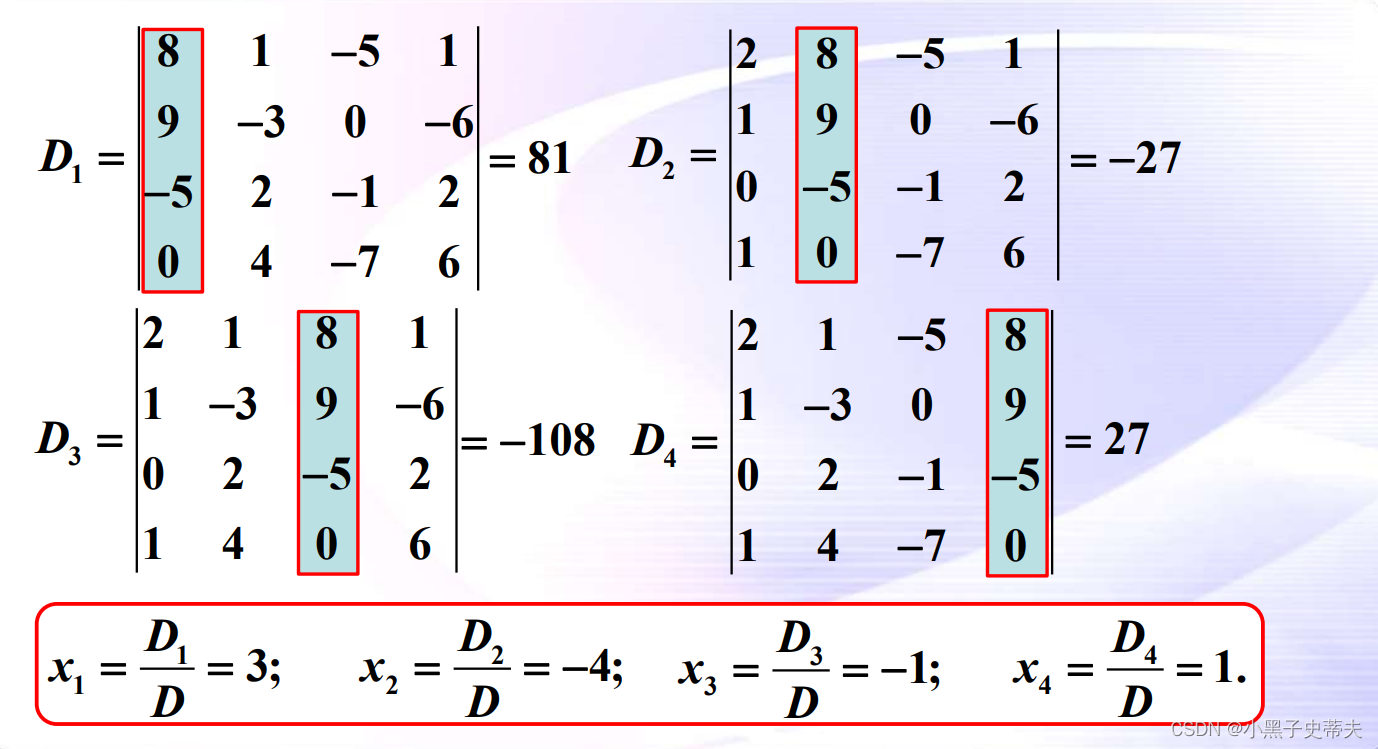
案例：

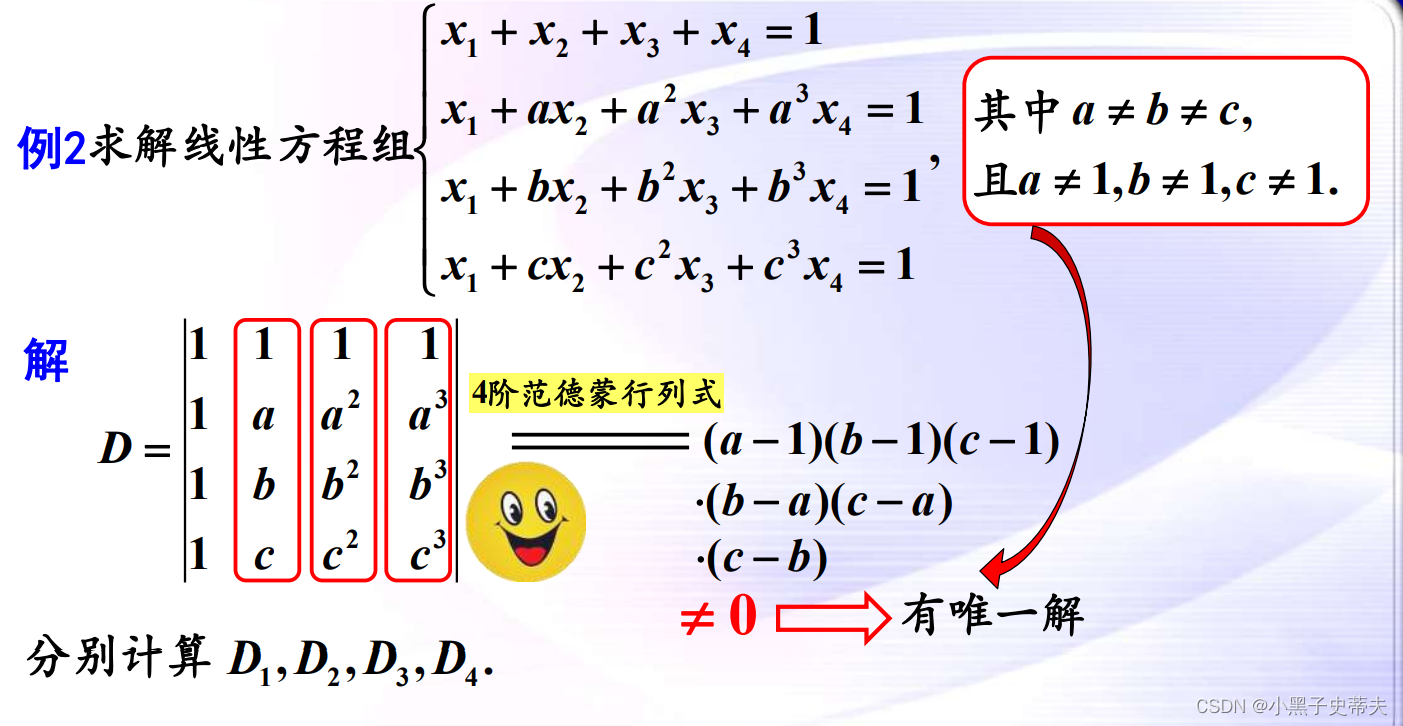
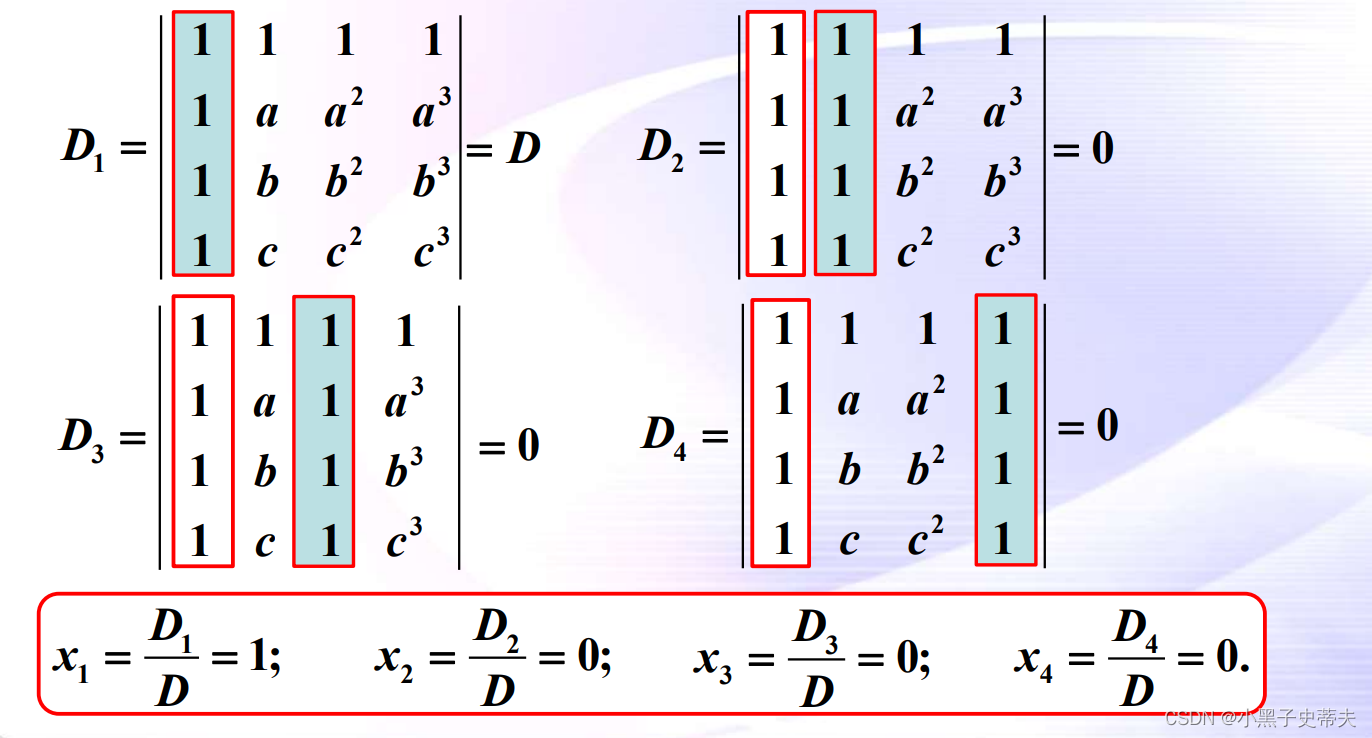
10.2 齐次线性方程组

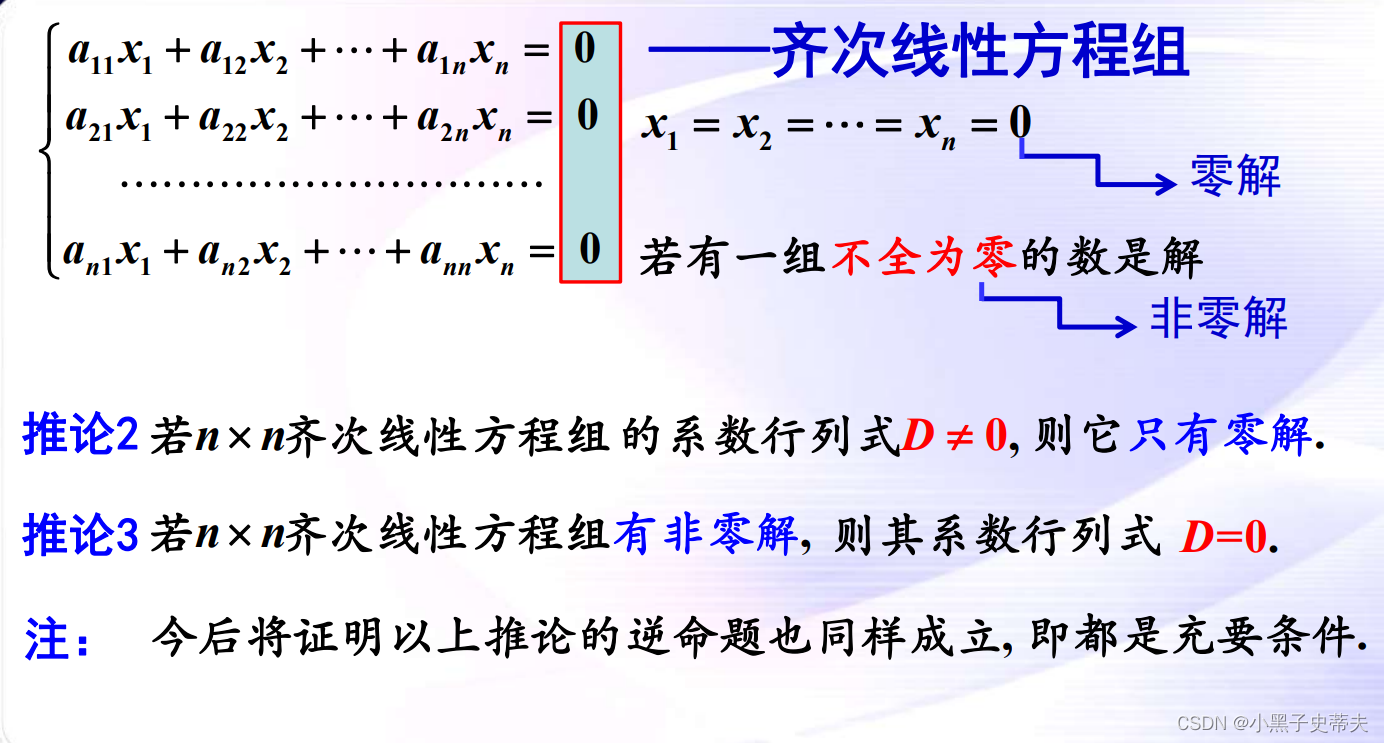
案例：