【分类评价指标】如何评估多（二）分类算法的性能：Acc、Precision、Recall、F1等

1. 前言

评价指标是针对模型性能优劣的一个定量指标。一种评价指标只能反映模型一部分性能，如果选择的评价指标不合理，那么可能会得出错误的结论，故而应该针对具体的数据、模型选取不同的评价指标。

本文将介绍分类任务中的常用评价指标。

• 二分类任务：混淆矩阵（Confuse Matrix）、准确率Acc（Accuracy）、精确率P（Precision）、召回率R（Recall）、F1 Score、P-R曲线（Precision-Recall Curve）、AP（Average-Precision）、ROC、AUC等；
• 多分类任务：Acc、各个类别的（P、R、F1、AP）、mAP（mean-Average-Precision）等。

2. 二分类任务

2.1 混淆矩阵

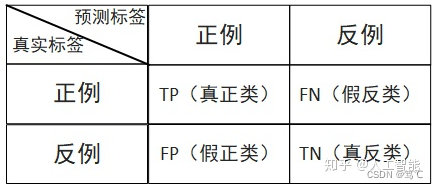
针对一个二分类问题，即将实例分成正类（positive）或负类（negative），在实际分类中会出现以下四种情况：

• 若一个实例是正类，并且被预测为正类，即为真正类TP(True Positive)
• 若一个实例是正类，但是被预测为负类，即为假负类FN(False Negative)
• 若一个实例是负类，但是被预测为正类，即为假正类FP(False Positive)
• 若一个实例是负类，并且被预测为负类，即为真负类TN(True Negative)

简单记忆：阳性(Positive)代表了预测为真，阴性(Negative)代表了预测为假；True代表真实值与预测值匹配，False代表真实值与预测值不匹配。

2.2 Accuracy、Precision、Recall、F1 Score

有了混淆矩阵之后，我们便可以求对应的准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1 Score。

2.2.1 准确率（Accuracy）

该指标计算的是：预测正确的样本数量占总量的百分比，具体的公式如下：

$Accurary=\frac{TP+TN}{TP+TN+FP+FN}$

• 缺点：当数据的样本不均衡，这个指标是不能评价模型的性能优劣的。
  假如一个测试集有正样本99个，负样本1个。模型把所有的样本都预测为正样本，那么模型的Accuracy为99%，看评价指标，模型的效果很好，但实际上模型没有任何预测能力。

2.2.2 精确率（Precision）

又称为查准率，是针对预测结果为正类的一个评价指标。在模型预测为正样本的结果中，真正是正样本所占的百分比，具体公式如下：

$Precision=\frac{TP}{TP+FP}$

• 精准率的含义：在预测为正样本的结果中，有多少是准确的。这个指标比较谨慎，分类阈值较高。

2.2.3 召回率(Recall)

又称为查全率，是针对原始样本而言的一个评价指标。在实际为正样本中，被预测为正样本所占的百分比。具体公式如下：

$Recall=\frac{TP}{TP+FN}$

• 尽量检测数据，不遗漏数据，所谓的宁肯错杀一千，不肯放过一个，分类阈值较低。

2.2.4 F1 Score

精准率和召回率都有其自己的缺点：

• 如果阈值较高，那么精准率会高，但是会漏掉很多数据；
• 如果阈值较低，召回率高，但是预测的会很不准确。

2.2.4.1 例子1

假设总共有10个好苹果，10个坏苹果。针对这20个数据，模型只预测了1个好苹果，对应结果如下表：

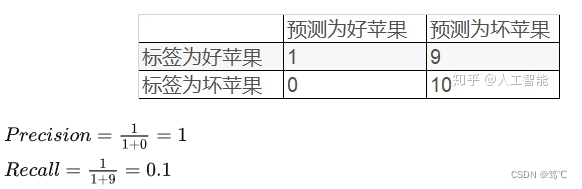
• 虽然精确率很高，但是这个模型的性能并不好。

2.2.4.2 例子2

同样总共有10个好苹果，10个坏苹果。针对这20个数据，模型把所有的苹果都预测为好苹果，对应结果如下表：

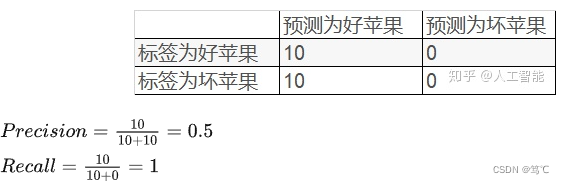
• 虽然召回率很高，但是这个模型的性能并不好。

2.2.4.3 解决办法

从上述例子中，可以看到精确率和召回率是此消彼长的，如果要兼顾二者，就需要F1 Score。

$F1=2\cdot \frac{Precision\times Recall}{Precision+Recall}$

可以看出F1 Score实际上是一种调和平均数。

• 此外还有$F_{\beta }$ score和 G score，也是用于平衡精确率和召回率的：

  $F_{\beta }=(1+{\beta }^2)\cdot \frac{Precision\times Recall}{{(\beta }^2\cdot Precision)+Recall}$

  $G=\sqrt{Precision\cdot Recall}$

2.3 P-R曲线和AP

2.3.1 P-R曲线

P-R曲线是描述精确率和召回率变化的曲线。

如何绘制：通过设置不同的阈值，模型进行预测，计算对应的精准率和召回率，然后进行绘制。

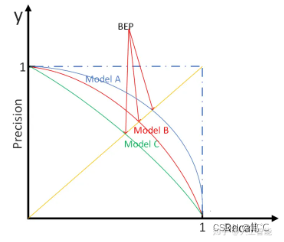
• 模型与坐标轴围成的面积越大，则模型的性能越好。但一般来说，曲线下的面积是很难进行估算的。
• 所以衍生出了“平衡点”（Break-Event Point，简称BEP），即当P=R时的取值，平衡点的取值越高，性能更优。

2.3.2 AP（Average-Precision）

P-R曲线对于单个类别的结果评价是比较完善的，但并没有数值那样直观，AP能够解决这个问题，AP值的含义是P-R曲线下的均值（P-R曲线的纵坐标即为Precision，因此AP含义即为Average-Precision），理论计算公式为：

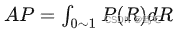
• 在实际程序中，由于本身是离散点，且得到所有点后再计算代价过高，一般采用专门的近似手段计算AP。常用的方法有两种，下面进行介绍。

假如验证了10个样本得到的预测结果如下表格，以这10个样本作为例子计算该类别的AP（程序中计算AP的方法），

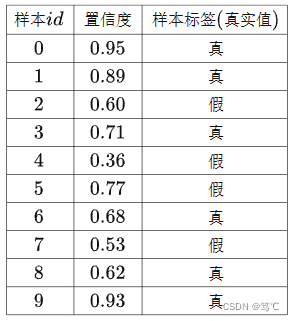
把这十个样本按照置信度由高到低的顺序排序，得到下面的表格：

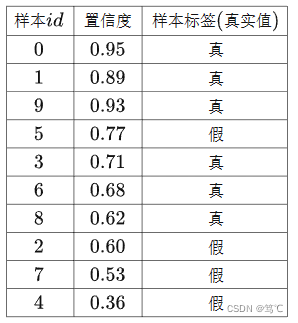
从上到下遍历每一行，遍历到某一行时就将置信度阈值设定为当前该行的置信度，即当前行是最低预测为正例的样本，然后计算在这个置信度阈值下的Precision、Recall，得到下面的表格：

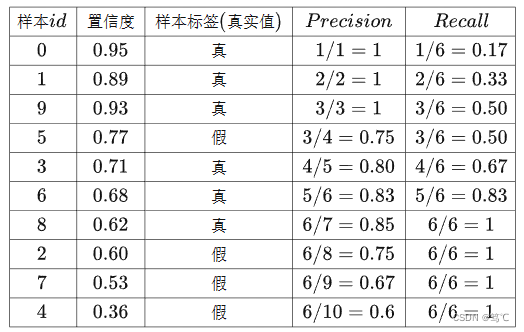
• 方法1：在VOC2010之前，方法是以列表[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]作为Recall分割值，遍历列表中每一个值作为Recall阈值，选取上面表格中Recall≥Recall阈值的所有行，这些行中最高的Precision即为这个Recall阈值对应的Precision取值，可以得到上面的表格对应的Precision列表为：[1, 1, 1, 1, 1, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85]，这个列表求和除以11极为AP计算结果：10.1 / 11 = 91.82%。
• 方法2：在VOC2010之后，方法是以Recall的所有可能取值再加上0作为Recall分割值，Recall的所有可能取值只与样本中正样本的数量有关，例如上面表格，只有6个正样本，因此就有6个可能的取值，再加上0，列表[0, 0.17, 0.33, 0.50, 0.67, 0.83, 1.0]就作为Recall分割值，然后和第一种方法类似，遍历列表中每一个值作为Recall阈值，选取上面表格中Recall≥Recall阈值的所有行，这些行中最高的Precision即为这个Recall阈值对应的Precision取值，可以得到上面的表格对应的Precision列表为：[1, 1, 1, 1, 0.85, 0.85, 0.85]，这个列表求和除以列表长度即为AP计算结果：6.55 / 7 = 93.57%。

2.4 ROC曲线和AUC

2.4.1 ROC的由来（例子3）

假设有好苹果9个，坏苹果1个，模型把所有的苹果均预测为好苹果。

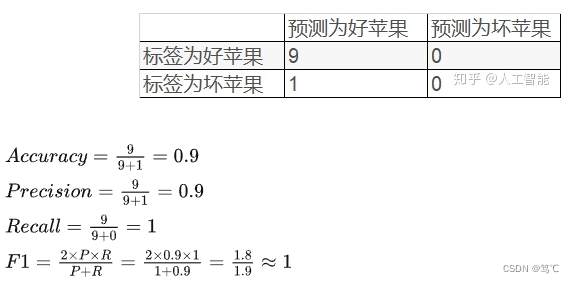
• 我们能够得出，尽管 Precision、Recall、F1都很高，但是模型效果却不好。
• 所以针对样本不均衡，以上指标很难区分模型的性能，就需要用到ROC和AUC。

2.4.2 先验概念

在介绍ROC和AUC之前，我们需要明确以下三个概念：

• 真正类率（true positive rate, TPR），也称为灵敏度(sensitivity)，等同于召回率。刻画的是被分类器正确分类的正实例占所有正实例的比例。
  
• 真负类率（true negative rate, TNR），也称为特异度(specificity)，刻画的是被分类器正确分类的负实例占所有负实例的比例。
  
• 负正类率（false positive rate, FPR），也称为1-specificity，计算的是被分类器错认为正类的负实例占所有负实例的比例。
  

2.4.3 ROC曲线

ROC（Receiver Operating Characteristic）曲线，又称接受者操作特征曲线。曲线对应的纵坐标是TPR，横坐标是FPR。

如何绘制：设置不同的阈值，会得到不同的TPR和FPR，而随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着负类，即TPR和FPR会同时增大。阈值最大时，对应坐标点为（0,0），阈值最小时，对应坐标点（1,1）。

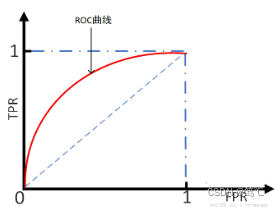
• 目标： TPR=1, FPR=0，即图中(0,1)点。故ROC曲线越靠拢(0,1)点，即，越偏离45度对角线越好。对应的就是TPR越大越好，FPR越小越好。

2.4.4 AUC

AUC(Area Under Curve)是处于ROC曲线下方的那部分面积的大小。AUC越大，代表模型的性能越好。

• 对于2.4.1例子中的样本不均衡，对应的TPR=1，而FPR=1，能够判断模型性能不好。

如何计算AUC：

• auc的值是求roc的积分，但是求积分比较困难，所以通过转化，变为另一种求解，可查看：Wilcoxon-Mann-Witney Test。
• 所以最终的AUC求解是通过如下公式计算所得，还需要注意的是当二元组中正负样本的预测分数相等的时候，按照0.5计算。
  

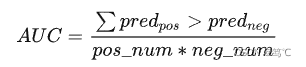
2.5 二分类指标小结

• 当正负样本差距不大的情况下，ROC和PR的趋势是差不多的；
• 但是当负样本很多的时候，两者就截然不同了，P-R效果依然看似很好，但是ROC上反映效果一般。

3. 多分类任务

3.1 准确率

对于多分类任务，最直接的评价指标即为考虑全类别的准确率，即

$Accurary=\frac{分类正确的样本数}{总样本数}$

• 分类正确即只考虑预测的类别和真实的类别对应正确的情况。这是最常用也最直接的评价指标，一般模型训练过程中打印出来查看的也主要是指这个准确率。

3.2 各个类别的P、R、F1、AP

如二分类评价指标最初的说明，多分类任务可以采用二分类的手段：

• 独立地对每个类别进行评估得到每个类别的多个二分类评价指标，这些指标可以较为准确地反映各个类别的结果情况。

因此，

• 多分类任务中的P、R、F1即分别将每个类别单独进行考察，得到每个类别的P、R、F1指标，需要注意的是，得到P、R、F1指标就说明已经确定了置信度阈值，因此P、R指标是与置信度阈值有关系的指标，设定不同的置信度阈值会导致不一样的结果。
• 多分类任务中的AP也与二分类中的一致，需要注意的是，AP是与置信度阈值无关的指标，能够更客观反映结果好坏。

3.3 mAP

对所有类别的AP求平均即可得到mAP指标，代表的含义即mean-Average-Precision，其中mean是对所有类别求平均。

4. 参考

【1】https://zhuanlan.zhihu.com/p/371819054
【2】https://zhuanlan.zhihu.com/p/110015537