MATLAB/Simulink 通信原理及仿真学习（三）

3. 通信信号与系统分析

• 数字通信的研究包括数字形式的信息从产生该信息的信源到一个或多个目的地的传输问题。

3.1 离散信号和系统

• 信号是信息的物理表现形式或说是传递信息的函数，系统定义为处理（或变换）信号的物理设备。

3.1.1 离散信号

一个信号$x(t)$可以是连续时间信号（模拟信号），也可以是离散时间信号（数字信号）。若$x(t)$是离散信号，则$t$仅在时间轴的离散点上取值，这时，应将$x(t)$该记为$x(n{T}_s)$，$T_s$表示相邻两个点之间的时间间隔，又称抽样周期，$n$取整数，即
$$\begin{array}{c}x(n{T}_s),n=-N_1,\cdots ,0,1,\cdots ,N_2\end{array}\text{\hspace{1em}(3-1)}$$

式中，$N_1,N_2$是$n$的取值范围。一般可以把$T_s$归一化为1，则$x(n{T}_s)$可简记为$x(n)$。

(一直没写MATLAB，差点忘了，注释的符号是 %)

• 例一

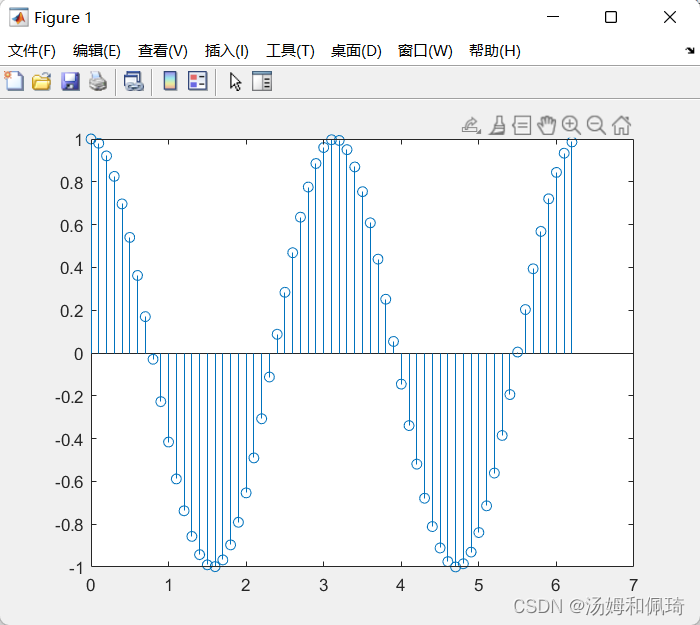
% x=cos(2t)，抽样序列为0<=t<=2*pi，抽样周期T_s=0.1.
t=0:0.1:2*pi;
x=cos(2*t);
stem(t,x);

输出结果：

1）信号的相加或相乘
$$\{\begin{array}{l}x(n)=x_1(n)+x_2(n)\\ y(n)=x_1(n)x_2(n)\end{array}$$

• 例二

% 信号x1(n)=sin(2*pi*0.1n）和x2(n)=exp(-0.1*n)，
% 在0<=n<=40的相加和相乘序列
clear all;
n=1:40;
x1=sin(2*pi*0.1*n);
x2=exp(-0.1*n);
x=x1+x2;
y=x1.*x2;
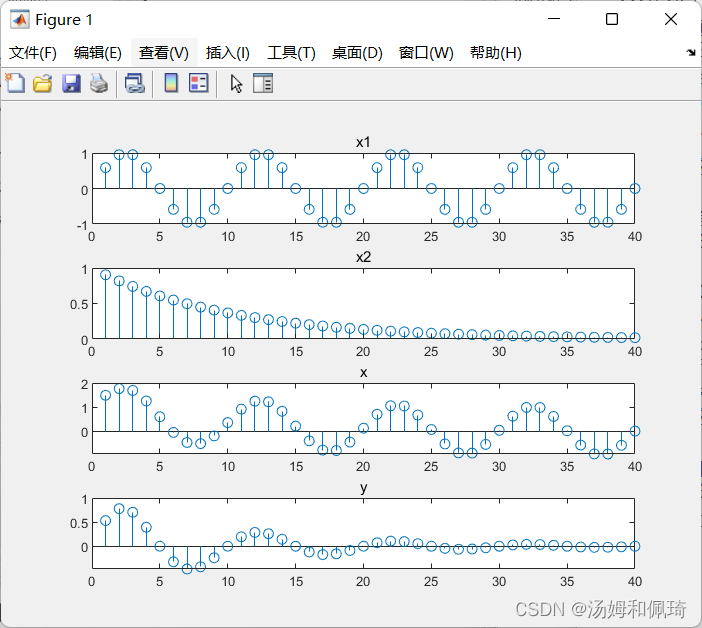
subplot(4,1,1);stem(n,x1);title('x1');
subplot(4,1,2);stem(n,x2);title('x2');
subplot(4,1,3);stem(n,x);title('x');
subplot(4,1,4);stem(n,y);title('y');

输出结果：

2）卷积和
$$y(n)=\sum _{m=-\infty }^{\infty }x(m)h(n-m)=x(n)\ast h(n)\text{\hspace{1em}(3-3)}$$

• 例三

% h(n)=exp(-0.1*n),x(n)=exp(-0.2*n),0<=n<=40的卷积和
clear all;
n=0:40;
h=exp(-0.1*n);
x=exp(-0.2*n);
y=conv(x,h);
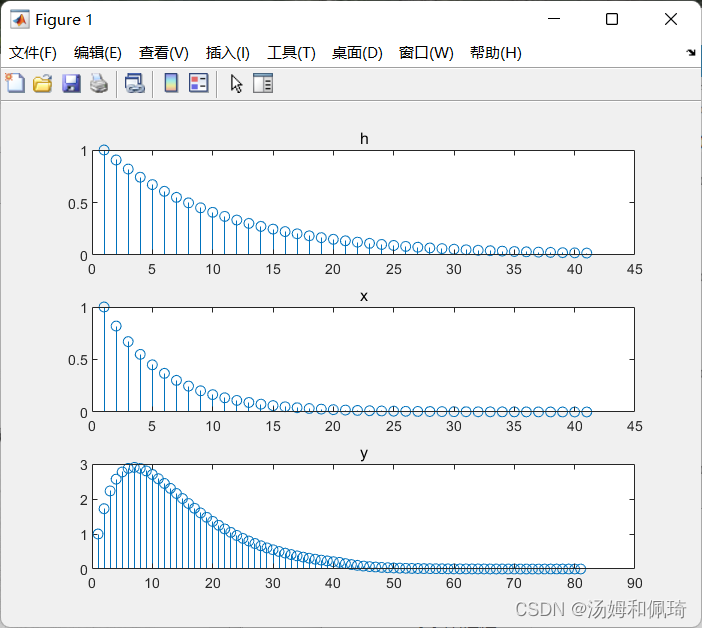
subplot(3,1,1);stem(h);title('h');
subplot(3,1,2);stem(x);title('x');
subplot(3,1,3);stem(y);title('y');

输出结果：

3.1.2 离散时间信号

• 离散时间系统可抽象为一种变换或一种映射，输入序列$x(n)$变换为输出序列$y(n)$，即

$$y(n)=T[x(n)]\text{\hspace{1em}(3-4)}$$
式中，$T$代表变换。
离散时间系统：

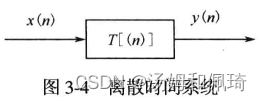
• 例四
  一个离散时间系统的输入和输出关系为：
  $$y(n)=ay(n-1)+x(n)\text{\hspace{1em}(3-5)}$$
  式中，a为常数。该系统表示，现在时刻的输入$y(n)$等于上一次的输出$y(n-1)$乘以常数a再加上现在的输入$x(n)$，这是一个一阶的自回归差分方程，若
  $$\begin{gathered} (1)x(n)=\{\begin{array}{l}1,n=0\\ 0,n\ne 0\end{array} \\ (2)x(n)=\{\begin{array}{ll}exp(-0.1n),& 0\le n\le 40\\ 0,& \text{其他}\end{array} \end{gathered}$$
  且$a=0.8,y(n)=0,n<0,y(0)=x(0)$，是分别求上述系统在所给输入下的响应。

clear all
N=60;%序列长度
% 设置x1和x2
x1=zeros(1,N);
x1(1)=1;
x2=zeros(1,N);
x2(1:41)=exp(-0.1*(0:40));
% 初始状态设置
y1(1)=x1(1);
y2(1)=x2(1);
% 求取y(n)
for n=2:N
 y1(n)=0.8*y1(n-1)+x1(n);
 y2(n)=0.8*y2(n-1)+x2(n);
end
% 绘图
subplot(4,1,1);stem(x1);title('x1');
subplot(4,1,2);stem(x2);title('x2');
subplot(4,1,3);stem(y1);title('y1');
subplot(4,1,4);stem(y2);title('y2');

输出结果

• 例五

一个离散时间系统的输入/输出关系为
$$y(n)=\sum _{k=0}^{M-1}b(k)x(n-k)\text{\hspace{1em}(3-6)}$$

式中，$b(0),b(1),\cdots ,b(M-1)$为常数。

这一类系统为“有限冲激响应”系统，简称为FIR系统（上一时刻的输出对下一时刻的输出没有影响）。一阶自回归模型中由于包含了由输出到输入的反馈，因此其冲激响应为无限长，这一类系统称为“无限冲激响应”系统，简称IIR系统(包含上一时刻的输出对下一时刻输出的影响)。

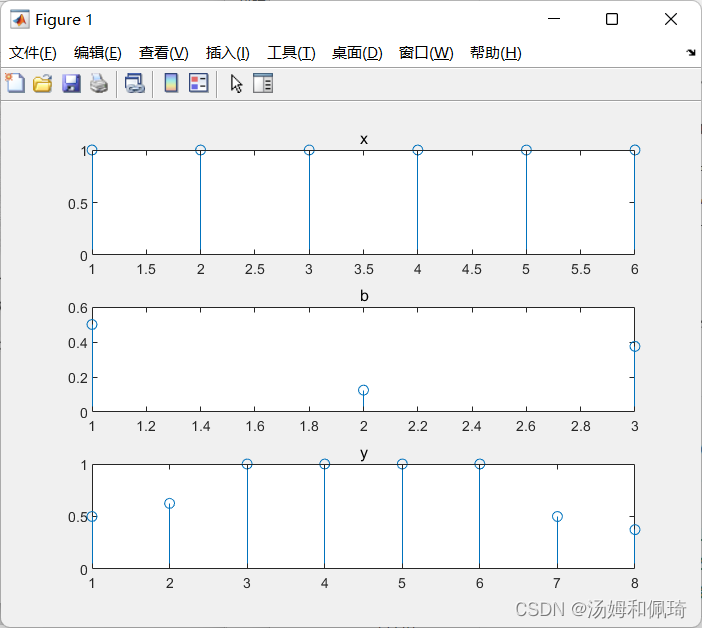
在式（3-6）中，设$M=3,b(0)=1/2,b(1)=1/8,b(2)=3/8,x(n)=\{\begin{array}{l}1,0\le n\le 5\\ 0,\text{其他}\end{array}$，试求其输出响应，

clear all
x = ones(1,6);
b = [1/2,1/8,3/8];
y=conv(x,b);
subplot(3,1,1);stem(x);title('x');
subplot(3,1,2);stem(b);title('b');
subplot(3,1,3);stem(y);title('y');

输出结果：

3.1.3 信号的能量和功率

• 能量定义：
  $$E={\int }_{-\infty }^{\infty }|x(t){|}^{2}dt\text{\hspace{1em}(3-7)}$$
  $$E=\sum _{-\infty }^{\infty }|x(n){|}^2\text{\hspace{1em}(3-8)}$$

如果$E<\infty$,称 $x(t),x(n)$为能量有限信号，简称能量信号；$E>\infty$,则称为能量无限信号。若$x(t)$和$x(n)$能量无限，往往开展其功率的研究，即
$$P=\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-T/2}^{T/2}|x(t){|}^{2}dt\text{\hspace{1em}(3-9)}$$
$$P=\underset{N\to \infty }{\lim }\frac{1}{2N+1}\sum _{n=-N}^N|x(n){|}^2\text{\hspace{1em}(3-10)}$$

若$P<\infty$，则称$x(t),x(n)$为功率有限信号，简称功率信号。

• 周期信号、准周期信号与随机信号，由于其时间是无限的，因而为功率信号。一般在有限区间内存在的确定信号是能量信号。例如：$x(n)=1,1\le n\le 100$是能量信号，$x(n)=sin(2\pi n),-\infty \le n\le \infty$是功率信号。

3.2 傅里叶（Fourier）分析

连续时间信号的Fourier变换和Fourier级数，数字信号处理中的离散Fourier变换（DFT）。

3.2.1 连续时间信号的Fourier变换

设$x(t)$为以连续时间信号，若$x(t)$绝对可积，即
$${\int }_{-\infty }^{\infty }|x(t)|dt<\infty \text{\hspace{1em}(3-11)}$$
那么，$x(t)$的Fourier变换存在，并定义为：
$$X(j\Omega )={\int }_{-\infty }^{\infty }x(t)e^{-j\Omega t}dt\text{\hspace{1em}(3-12)}$$

其反变换为：
$$x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }X(j\Omega )e^{j\Omega t}d\Omega \text{\hspace{1em}(3-13)}$$

式中，$\Omega =2\pi f$，单位为rad/s，将$X(j\Omega )$表示成$|X(j\Omega )|e^{j\phi (\Omega )}$的形式，即可得到$|X(j\Omega )|$和$\phi (\Omega )$随 变化的曲线，分别成为幅频特性和相频特性。

• 例六

绘制$f(t)=t{e}^{-|t|}$的时域波形及傅里叶变化后的幅频特性。

clear all
% 定义符号变量t
syms t;
f = t*exp(-abs(t));
F = fourier(f)
% 绘制函数曲线
subplot(1,2,1);ezplot(f);
subplot(1,2,2);ezplot(abs(F));

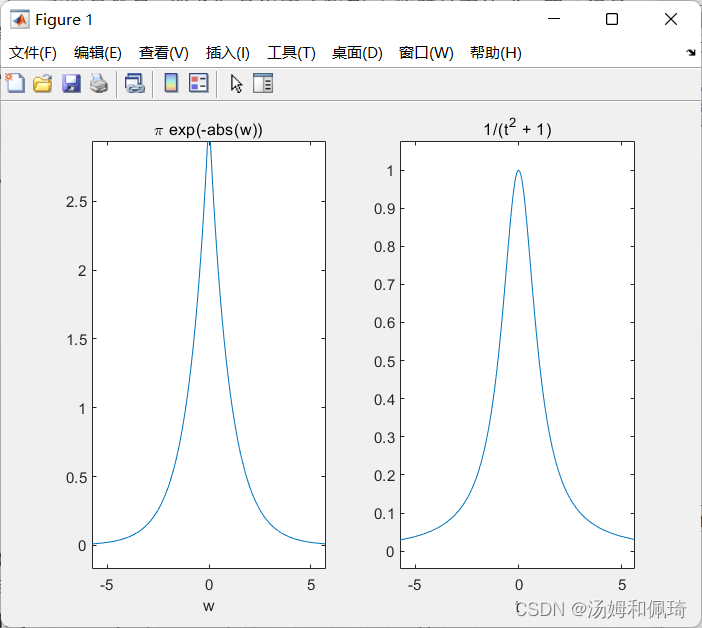
• 例七

某信号的Fourier变换$F(\omega )=\pi e^{-|\omega |}$，试绘制该信号的时域波形和幅频特性。

clear all
syms t w;
F = pi*exp(-abs(w));
f = ifourier(F,t);
subplot(1,2,1);ezplot(abs(F));
subplot(1,2,2);ezplot(f);

• 严格而将只有非周期函数才有Fourier变换，但若$x(t)$是周期函数，即 ，此时不满足（3-11）的绝对可积条件，此时要求$x(t)$​满足狄利克雷条件（Dirichlet），即：（1 ）在一周期内，连续或只有有限个第一类间断点（该点含有左右极限）；（2）在一周期内，极大值和极小值的数目应是有限个；（3）在一周期内，信号是绝对可积的。

• Fourier级数为：
  $$x(t)=\sum _{k=-\infty }^{\infty }X(k{\Omega }_0)e^{jk{\Omega }_{0}t},k=0,\pm 1,\cdots ,\pm \infty \text{\hspace{1em}(3-14)}$$
  其中${\Omega }_0=2\pi /T_0=2\pi f_0$，为信号$x(t)$的基波频率，$k{\Omega }_0$为其第k次谐波频率：$X(k{\Omega }_0)$称为$x(t)$在k次谐波处的Fourier系数，它的幅度反映了信号$x(t)$中所包含的频率为$k{\Omega }_0$的成分大小。

• 可以看出周期信号$x(t)$可以由无数个复正弦$[e^{jk{\Omega }_{0}t},k=0,\pm 1,\cdots ,\pm \infty ]$ 作为基本信号再乘以不同的加权值$X(k{\Omega }_0)$复合而成。$X(k{\Omega }_0)$仅在${\Omega }_0$的整数倍上取值，所以其在频率轴上取离散值， 即：
  $$X(k{\Omega }_0)=\frac{1}{T}{\int }_t^{t+T}x(t)e^{-jk{\Omega }_{0}t}dt\text{\hspace{1em}(3-15)}$$
  其中$X(k{\Omega }_0)$是复数，所以
  $$X(k{\Omega }_0)=|X(k{\Omega }_0)|e^{j{\theta }_k}$$
  式中，$|X(k{\Omega }_0)|$是频率为$n{f}_0$的分量的振幅，${\theta }_k$是频率是$n{f}_0$的分量的相位。

• 注意$X(k{\Omega }_0)$和$X(j\Omega )$的物理意义不同，前者是$\Omega$轴上的离散函数，后者则是$\Omega$轴上的连续函数，同时前者是谐波幅度，后者是频谱密度。

• 例八(${\Omega }_0=2\pi /T$)
  

clear all
k=-50:50;
X=0.25*sinc(k/4);
stem(k,X)

3.2.2 离散时间信号的Fourier变换

• 设$h(n)$为一线形时不变系统的单位抽样响应，定义
  $$H(e^{j\omega })=\sum _{n=-\infty }^{\infty }h(n)e^{-j\omega n}\text{\hspace{1em}(3-20)}$$
  为系统的频率响应，记住了这是离散时间序列的Fourier变换（Discrete Time Fourier Transform, DTFT）。$H(e^{j\omega })$是$\omega$的连续函数，周期为$2\pi$ 。其中$\omega$为数字频率。（3-20）的DTFT是周期信号$H(e^{j\omega })$在频域内展开成的Fourier级数，其Fourier系数是时域信号$h(n)$。

• 离散信号$h(n)$的DTFT存在的条件是$h(n)$是绝对可和的，既满足：
  $$\sum _{n=-\infty }^{\infty }|h(n)|<\infty \text{\hspace{1em}(3-21)}$$

• 相应的，其DTFT反变换（IDTFT）可以表示为：
  $$h(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }H(e^{j\omega })e^{j\omega n}d\omega \text{\hspace{1em}(3-22)}$$
  根据上述DTFT的定义，可以利用MATLAB，由$h(n)$直接计算$H(e^{j\omega })$在频率区间 $[0,\pi ]$的值并绘制对应的模和相角。

• 假设序列$h(n)$在区间$n_1\le n\le n_2$有$N$个样本值，要计算其在下述频率点上的$H(e^{j\omega })$ ：
  $${\varpi }_k=k\frac{\pi }{M},k=0,1,\cdots ,M-1\text{\hspace{1em}(3-23)}$$
  首先定义一个$(M+1)\times N$ 的矩阵，即
  $$\mathbf{W}=W(k,n)=e^{-j(\frac{\pi }{M})kn},n_1\le n\le n_2,k=0,1,\cdots ,M-1\text{\hspace{1em}(3-24)}$$
  如果将 { k } \{k\} {k}和 { n } \{n\} {n}写为列矢量，则有
  $$\mathbf{W}=[e^{-j(\pi /M)K^{T}n}]\text{\hspace{1em}(3-25)}$$
  于是，在所求频率点上的$H(e^{j\omega })$值可以写为：
  $$H^T=h^T\ast \mathbf{W}\text{\hspace{1em}(3-26)}$$

• 例九
  

w = -4:0.001:4;
n1=-15:15;
n2=0:20;
h1=exp(-abs(0.1*n1));
h2(n2+1)=1;
Hjw1=h1*(exp(-j*pi).^(n1'*w));
Hjw2=h2*(exp(-j*pi).^(n2'*w));
subplot(2,1,1);plot(w,abs(Hjw1));
title('H1');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,1,2);plot(w,abs(Hjw2));
title('H2');xlabel('pi 弧度(w)');ylabel('振幅');

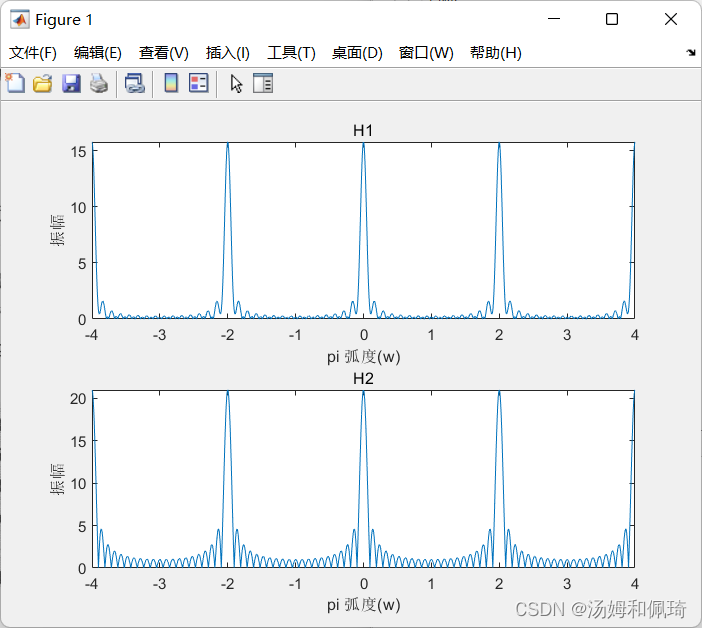
离散时间信号的Fourier变换的性质十分重要，如卷积性质、频移性质等。
DTFT的频移性质是指，序列乘以复指数序列对应于频域的频移，即
$$DTFT(h(n)e^{j{\omega }_{1}n})=H(e^{j(\omega -{\omega }_1)})\text{\hspace{1em}(3-27)}$$

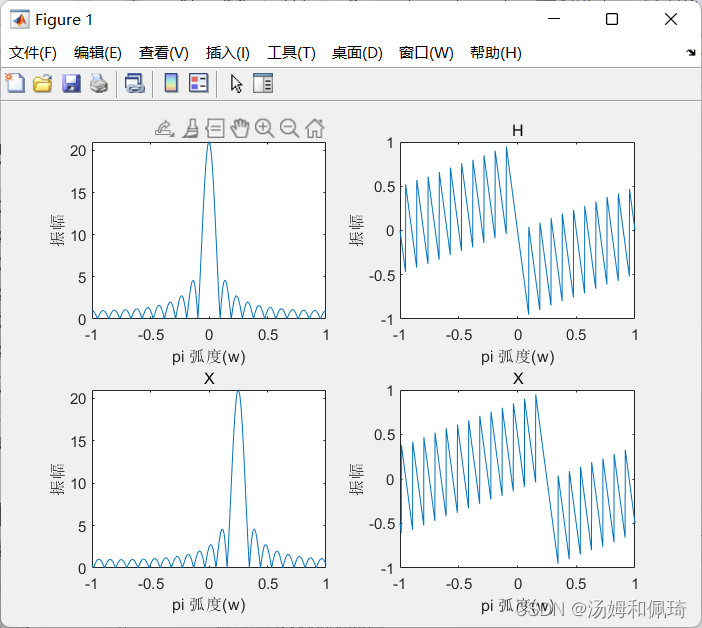
• 例十

给定序列$h(n)=1,0len\le 20$ 和 $x(n)=h(n)e^{j\pi n/4}$，分别计算它们的离散时间Fourier，并比较结果。

clear all
w=-1:0.001:1;
n=0:20;
h(n+1)=1;
x=h.*exp(j*pi*n/4);
Hjw=h*(exp(-j*pi).^(n'*w));
Xjw=x*(exp(-j*pi).^(n'*w));
subplot(2,2,1);plot(w,abs(Hjw));
title('H');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,2,2);plot(w,angle(Hjw)/pi);
title('H');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,2,3);plot(w,abs(Xjw));
title('X');xlabel('pi 弧度(w)');ylabel('振幅');
subplot(2,2,4);plot(w,angle(Xjw)/pi);
title('X');xlabel('pi 弧度(w)');ylabel('振幅');

一个单位脉冲响应为$h(n)$的系统对输入序列$x(n)$的输出为：
$$y(n)=x(n)\ast h(n)\text{\hspace{1em}(3-28)}$$
根据DTFT的卷积性质，有：
$$Y(e^{j\omega })=DTFT[y(n)]=DTFT[x(n)\ast h(n)]=X(e^{j\omega })H(e^{j\omega })\text{\hspace{1em}(3-29)}$$
可以利用这一性质求系统在输入信号为$x(n)$时的系统响应。可以先求出$X(e^{j\omega })$和$H(e^{j\omega })$,进而求出$Y(e^{j\omega })$，再通过IDTFT求出$y(n)$，绕过求卷积的步骤。

• 例11 一个系统的单位脉冲响应$h(n)=sin(0.2n)e^{-0.1n},0\le n\le 30$，试求：
  （1）该系统的频率响应；
  （2）若输入信号为$x(n)=2sin(0.2\pi n)+3cos(0.4\pi n),0\le n\le 30$，确定该系统的稳态输出。

clear all
w=-1:0.001:1;
n=0:30;
h=sinc(0.2*n);
x=2*sin(0.2*pi*n)+3*cos(0.4*pi*n);
Hjw=h*exp(-j*pi).^(n'*w);
Xjw=x*exp(-j*pi).^(n'*w);
Yjw=Xjw.*Hjw;
n1=0:2*length(n)-2;
dw=0.001*pi;
y=(dw*Yjw*(exp(j*pi).^(w'*n1)))/(2*pi);
y1=conv(x,h);
subplot(3,1,1);plot(w,abs(Hjw))
title('H');xlabel('pi 弧度（w）');ylabel('振幅');
subplot(3,1,2);plot(w,abs(Xjw))
title('X');xlabel('pi 弧度（w）');ylabel('振幅');
subplot(3,1,3);plot(w,abs(Yjw))
title('Y');xlabel('pi 弧度（w）');ylabel('振幅');

3.2.3 离散Fourier变换

• 3.2.2节学习的DTFT的特点是：（1）变换使用无限长的序列；（2）变换的结果是自变量$\omega$的连续函数。（时域上连续，在计算机的使用上很难实现。）因而需要一种时域和频域上都离散的计算方法，这便是离散Fourier变换（DFT），也成为快速Fourier变换（FFT）。
• 给定一个离散序列$x(n)$,其DFT和IDFT如下：

$$\{\begin{array}{l}X(k)=\sum _{n=0}^{N-1}x(n)e^{-j\frac{2\pi }{n}nk}=\sum _{n=0}^{N-1}x(n)W_N^{nk},k=0,1,\cdots ,N-1\\ x(n)=\frac{1}{N}\sum _{n=0}^{N-1}X(k)e^{j\frac{2\pi }{n}nk}=\frac{1}{N}\sum _{n=0}^{N-1}x(n)W_N^{-nk},n=0,1,\cdots ,N-1\end{array}\text{\hspace{1em}(3-30)}$$

式中，$W_N=e^{-j\frac{2\pi }{N}}$。DFT对应的是时域和频域都是有限长，且都是离散的。

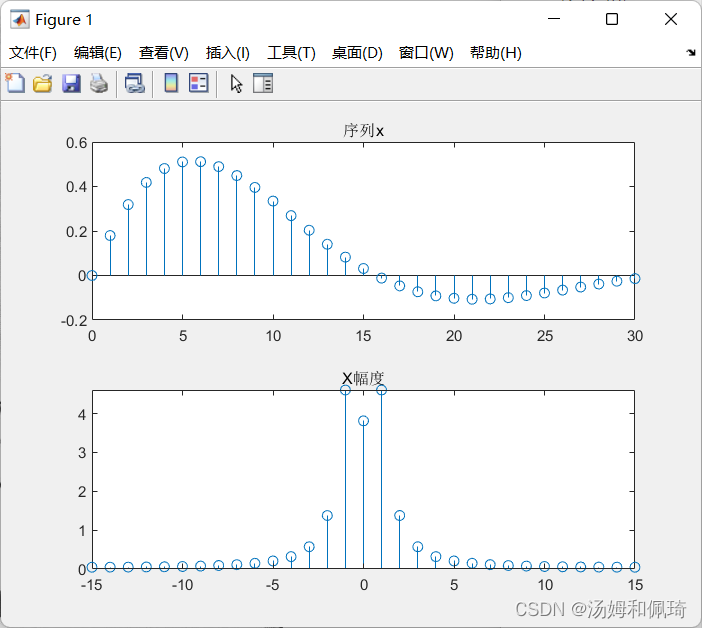
• 例十二 离散序列$x(n)=sin(0.2n)e^{-0.1n},0\le n\le 30$，试求该序列的DFT。

clear all
n=0:30;
x=sin(0.2*n).*exp(-0.1*n);
k=-0:30;
N=31;
Wnk=exp(-j*2*pi/N).^(n'*k);
X=x*Wnk;
subplot(2,1,1);stem(n,x);title('序列x');
% DFT默认的下标范围是[0,N-1],采取对下标的重新排列，
% 体现序列DFT的对称性
subplot(2,1,2);stem(-15:15, [abs(X(17:end)) abs(X(1:16))]);title('X幅度');

输出结果

• MATLAB提供fft函数计算优先离散序列的DFT，DFT的循环卷积性质，可以设序列$x(n),h(n)$都是N点序列，其DFT分别是$X(k),H(k),Y(k)$，若

则
$$Y(k)=X(k)H(k)\text{\hspace{1em}(3-32)}$$

式中圈中间一个N的符号表示做N点循环卷积。

• 一般对两个N点序列的循环卷积，其矩阵形式如下：
  $$y=\left[\begin{array}{c}y(0)\\ y(1)\\ ⋮\\ y(N-1)\end{array}\right]=\left[\begin{array}{cccc}& h(0)& h(N-1)& \cdots h(1)\\ & h(1)& h(0)& \cdots h(2)\\ & ⋮& ⋮& ⋮\\ & h(N-1)& h(N-2)& \cdots h(2)\end{array}\right]\cdot \left[\begin{array}{c}x(0)\\ x(1)\\ ⋮\\ x(N-1)\end{array}\right]=\mathbf{H}\cdot \mathbf{x}\text{\hspace{1em}(3-33)}$$

式（3-33）中矩阵$H$成为循环矩阵，由第1行开始，依次向右移动一个元素，移出去的元素在下一行的最左边出现，即每一行都是由$h(0),h(N-1),\cdots ,h(1)$这N个元素依此法则移动所生成的，故成为$H$为循环矩阵，因此对应的卷积为循环卷积。

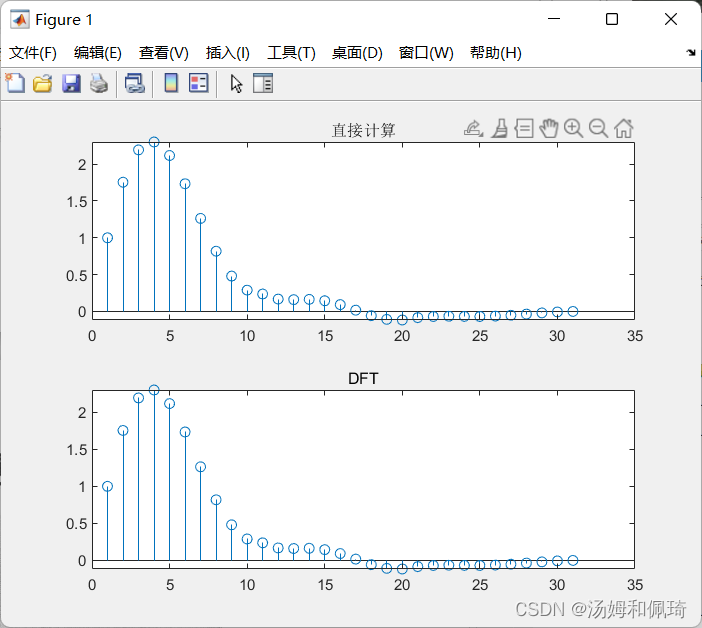
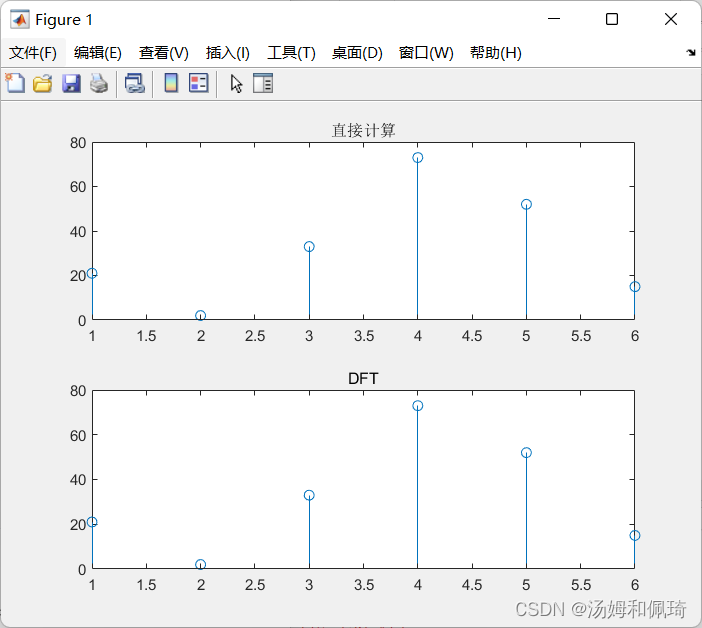
• 例十三

已知序列$h(n)=6,3,4,2,1,-2,x(n)=3,2,6,7,-1,-3)$，试分别用直接法和DFT，求两个序列的循环卷积序列。

% examp-13
clear all
h = [6 3 4 2 1 -2];
x = [3 2 6 7 -1 -3];
% 反转序列h
h1=fliplr(h);
% 利用toeolitz生成循环矩阵
H=toeplitz(h,[h(1) h1(1:5)]);
y=H*x';

H=fft(h);
X=fft(x);
Y=H.*X;
y1=ifft(Y);

subplot(2,1,1);stem(y);title('直接计算')
subplot(2,1,2);stem(y1);title('DFT')

输出结果：

• 设$x(n)$为一$M$点序列，$h(n)$为一$L$点序列，$y(n)=x(n)\ast h(n)$，即$y(n)$是$x(n)$和$h(n)$的线性卷积，那么$y(n)$是一$(M+L-1)$点的序列。由上面的讨论可知，DFT对应循环卷积而不对应线性卷积。如果利用DFT计算两个序列的线性卷积，则可以采用以下方法：

• 例十四

  已知序列$h(n)=sinc(0.2n),0\le n\le 20,x(n)=e^{-0.2n},0\le n\le 10$，试分别用直接法和DFT法求两个序列的线性卷积序列。

  %exmap-14
  clear all
  n1=0:20;
  n2=0:10;
  h=sinc(0.2*n1);
  x=exp(-0.2*n2);
  y=conv(x,h);
  
  % 补齐M+L-1的长度
  h1=[h zeros(1,length(x)-1)];
  x1=[x zeros(1,length(h)-1)];
  H1=fft(h1);
  X1=fft(x1);
  Y1=H1.*X1;
  y1=ifft(Y1);
  
  subplot(2,1,1);stem(y);title('直接计算');
  subplot(2,1,2);stem(y1);title('DFT');
  

输出结果