电子技术——负反馈特性

本节我们进一步深入介绍负反馈特性。
增益脱敏性
假设 β \beta β 是一个常数。考虑下面的微分方程:
d A f = d A ( 1 + A β ) 2 dA_f = \frac{dA}{(1 + A\beta)^2} dAf=(1+Aβ)2dA
将上式除以 A f = A 1 + A β A_f = \frac{A}{1+A\beta} Af=1+AβA 得到:
d A f A f = 1 1 + A β d A A \frac{dA_f}{A_f} = \frac{1}{1+A\beta}\frac{dA}{A} AfdAf=1+Aβ1AdA
这里 d A f A f \frac{dA_f}{A_f} AfdAf 指的是 A f A_f Af 的变化百分比, d A A \frac{dA}{A} AdA 指的是 A A A 的变化百分比,这说明负反馈将不稳定的 A A A 的变化降低了 1 + A β 1+A\beta 1+Aβ ,也就是反馈量的倒数倍,称为增益脱敏性。
带宽增加
考虑一个单极点的放大器的高频响应方程为:
A ( s ) = A M 1 + s / ω H A(s) = \frac{A_M}{1 + s/\omega_H} A(s)=1+s/ωHAM
则负反馈方程为:
A f ( s ) = A ( s ) 1 + β A ( s ) = A M / ( 1 + A M β ) 1 + s / ω H ( 1 + A M β ) A_f(s) = \frac{A(s)}{1 + \beta A(s)} = \frac{A_M / (1+A_M \beta)}{1 + s / \omega_H (1 + A_M\beta)} Af(s)=1+βA(s)A(s)=1+s/ωH(1+AMβ)AM/(1+AMβ)
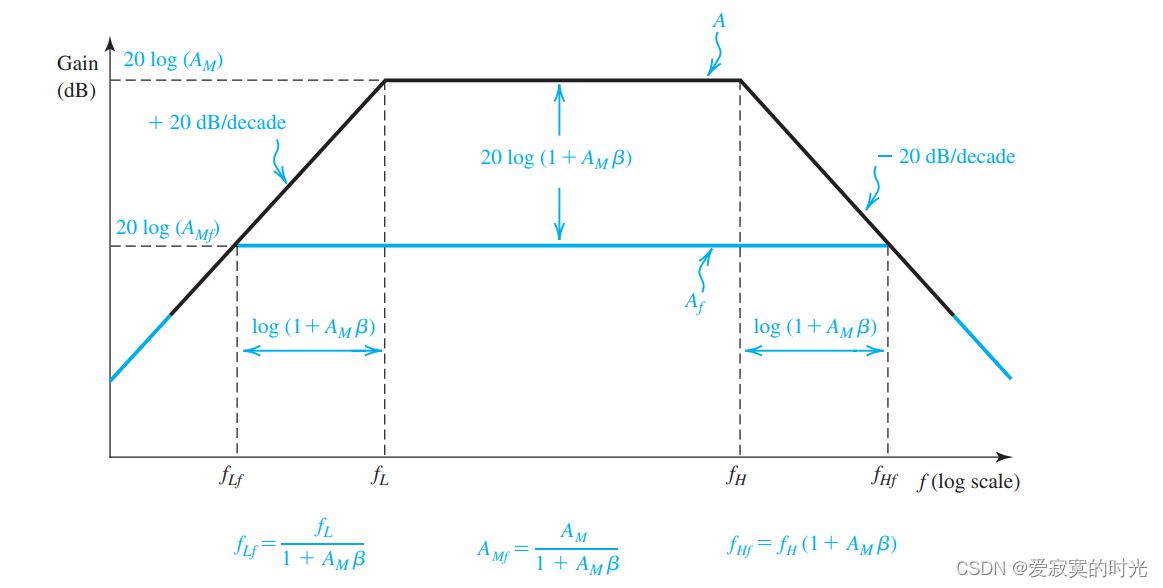
这说明,中频带增益降低到了 A M / ( 1 + A M β ) A_M / (1+A_M \beta) AM/(1+AMβ) 但是 − 3 d B -3dB −3dB 频率点增加到了:
ω H f = ω H ( 1 + A M β ) \omega_{Hf} = \omega_H (1 + A_M\beta) ωHf=ωH(1+AMβ)
同样的方法我们可以证明,对于具有低频响应的放大器,其低频 − 3 d B -3dB −3dB 点减小到:
ω L f = ω L 1 + A M β \omega_{Lf} = \frac{\omega_L}{1 + A_M \beta} ωLf=1+AMβωL
我们发现,具有负反馈的放大器的带宽增加,代价就是中频带增益减小,保证了增益带宽积不变。
减少干扰
负反馈可以减少噪声信号的干扰。然而,减少干扰只在特定的情况下起作用,考虑下面的情况:
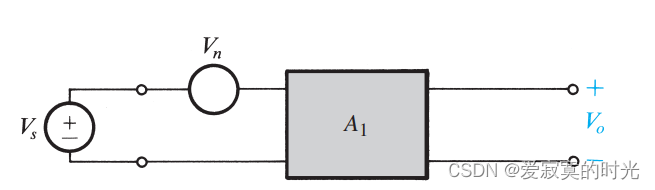
上图是一个受到
V
n
V_n
Vn 干扰的信号源。输出信号由叠加定理得到:
V o = V s A 1 + V n A 1 V_o = V_s A_1 + V_n A_1 Vo=VsA1+VnA1
我们定义 输出信噪比 为源信号分量除以噪声信号分量,则此时的输出信噪比我们记为:
S / I = V s A 1 V n A 1 = V s V n S/I = \frac{V_s A_1}{V_n A_1} = \frac{V_s}{V_n} S/I=VnA1VsA1=VnVs
接下来考虑下面的情况:
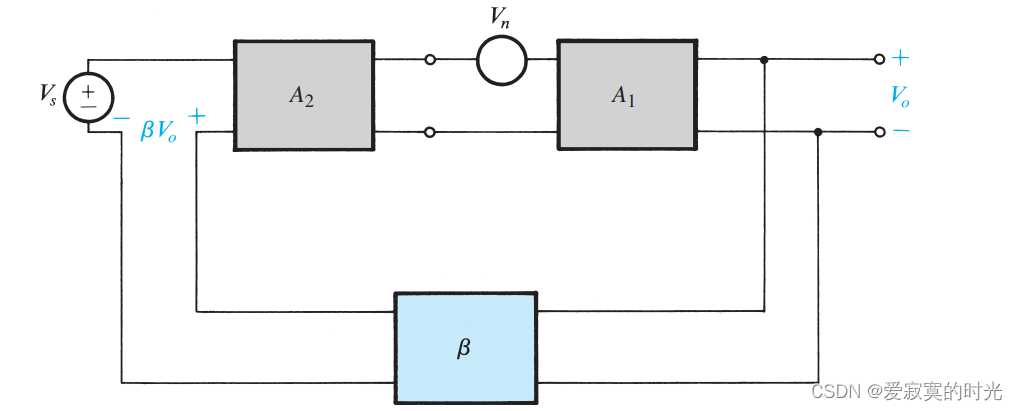
我们此时使用两个放大器,
A
2
A_2
A2 放大器不受输入端信号干扰,而原始
A
1
A_1
A1 端受到信号
V
n
V_n
Vn 的干扰,我们使用负反馈网络保证整体的增益不变,由叠加定理可以写出:
V o = V s A 1 A 2 1 + A 1 A 2 β + V n A 1 1 + A 1 A 2 β V_o = V_s \frac{A_1A_2}{1 + A_1A_2 \beta} + V_n \frac{A_1}{1 + A_1A_2 \beta} Vo=Vs1+A1A2βA1A2+Vn1+A1A2βA1
则此时的输出信噪比为:
S / I = V s V n A 2 S/I = \frac{V_s}{V_n} A_2 S/I=VnVsA2
比原来提升了 A 2 A_2 A2 倍。
我们强调这种方法必须要求在源放大器前端联级一个不受输入干扰的放大器。这很常见,例如在音频放大系统中,最后一级通常是功率输出级,功率输出级会出现 电源嗡嗡声 的问题,这是由于功率输出级需要提供较大的电流,从而提供较大的功率,由于电源电流越大功率越大,电源的纹波就会越大,就会收到较大的电源输入噪声干扰,另外对于大功率滤波的成本和代价是比较昂贵的。功率输出级不需要较大的电压增益,但是需要较大的功率增益,因此我们可以在功率输出级之前联级一个具有较大增益的小信号放大器,该放大器不需要较大的电流,因此可以使用功率较小的电源,此时纹波更小,可以视为无输入干扰,然后通过整体的负反馈网络控制整体电压增益。此时就可以有效的减小电源嗡嗡声的问题。我们称较大增益的小信号放大器为 前置放大器 。
减小非线性失真
下图展示了一个放大器输入和输出之间的关系(a):
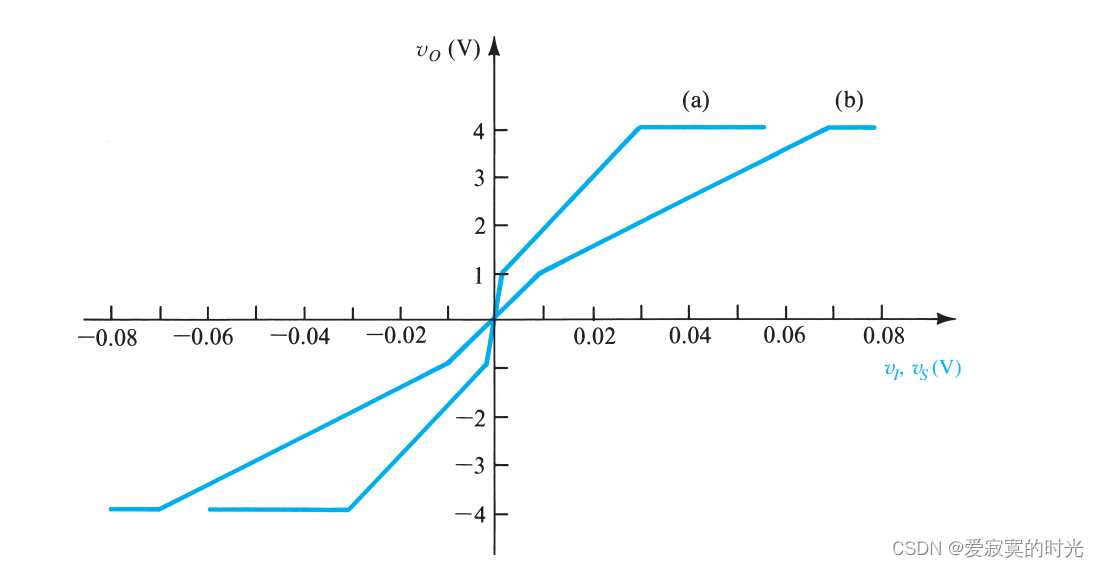
上面的传输函数的图像(a)是分段线性的,而不是整体线性的,因此,若输入一个较大的信号则会造成较大的非线性失真。
非线性失真的问题可以通过负反馈解决,我们称为 线性化 。假设我们使用的负反馈中 β = 0.01 \beta = 0.01 β=0.01 ,并且假设图像(a) 中斜率最大的那一段的斜率为 1000 1000 1000 另外一段的斜率为 100 100 100 。此时引入负反馈之后的斜率变成了:
A f 1 = 1000 1 + 1000 × 0.01 = 90.9 A_{f1} = \frac{1000}{1 + 1000 \times 0.01} = 90.9 Af1=1+1000×0.011000=90.9
A f 2 = 100 1 + 100 × 0.01 = 50 A_{f2} = \frac{100}{1 + 100 \times 0.01} = 50 Af2=1+100×0.01100=50
此时对应图像(b),我们发现图像整体变得更加的线性。但是代价是降低了放大器的增益,若想恢复增益,我们可以使用前置放大器,前置放大器不受非线性失真的影响,因为前置放大器处理小信号。
最后需要注意的,若放大器进入饱和区,则此时负反馈失效。因为此时增益变得非常非常小几乎是零,反馈量接近单位一。