目录
- 题目思路
- 回溯法
题目来源
40.组合总和II
题目思路
这道题目和39.组合总和如下区别:
- 本题candidates 中的每个数字在每个组合中只能使用一次。
- 本题数组candidates的元素是有重复的,而39.组合总和是无重复元素的数组candidates
为了理解去重我们来举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了)
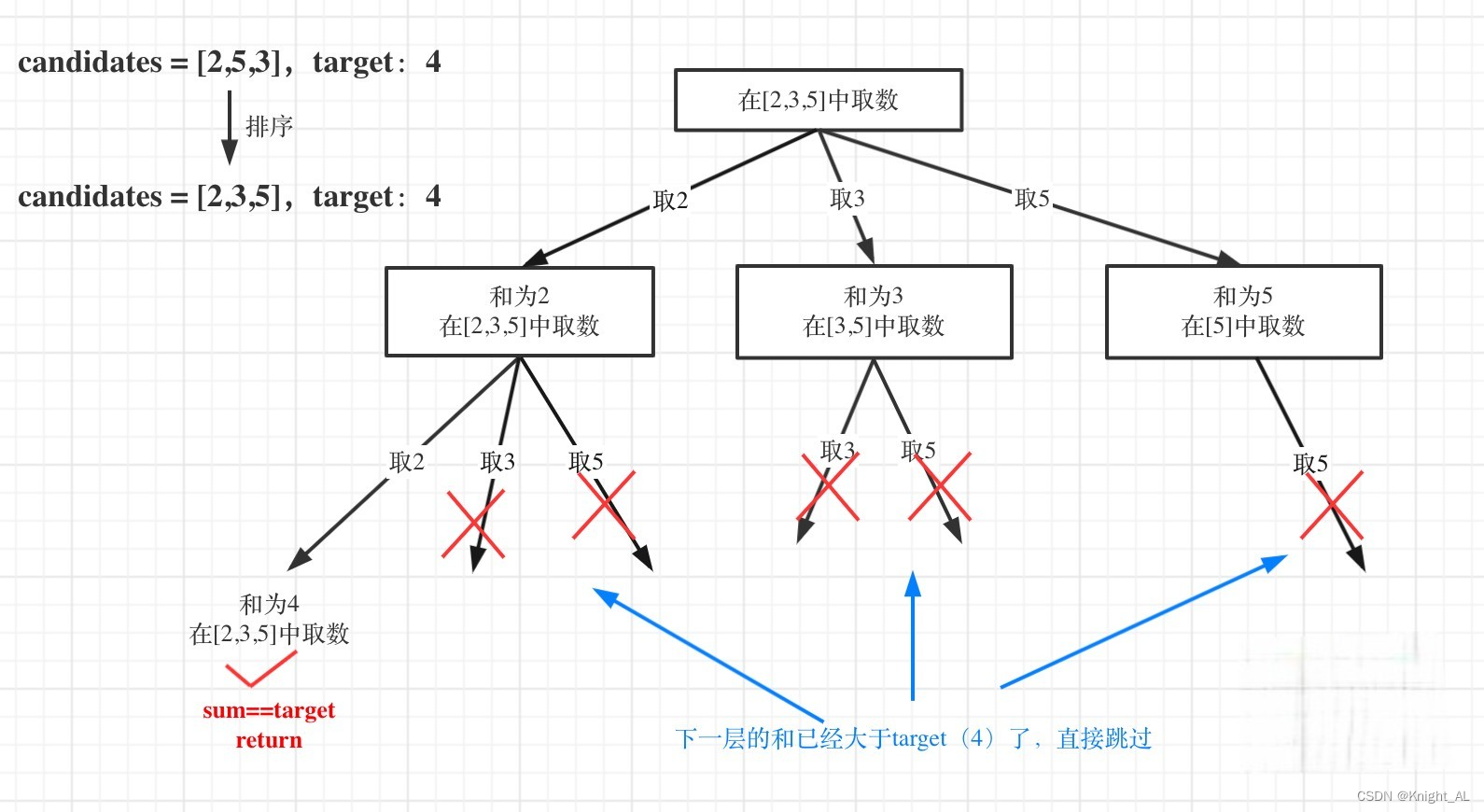
可以看出,每个节点相对于 39.组合总和我多加了used数组
回溯法
- 1.递归函数参数
与39.组合总和套路相同,此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
这个集合去重的重任就是used来完成的。
代码如下:
ArrayList<List<Integer>> result = new ArrayList<>(); // 存放组合集合
ArrayList<Integer> path = new ArrayList<>(); // 符合条件的组合
boolean[] used;
void backtracking(int[] candidates, int target,int sum,int startIndex,boolean[] used)
- 2.递归终止条件
终止条件为 sum > target 和 sum == target。
if (sum > target) { // 这个条件其实可以省略
return;
}
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
sum > target 这个条件其实可以省略,因为在递归单层遍历的时候,会有剪枝的操作
- 3.单层搜索的逻辑
要去重的是“同一树层上的使用过”,如何判断同一树层上元素(相同的元素)是否使用过了呢。
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。
此时for循环里就应该做continue的操作。
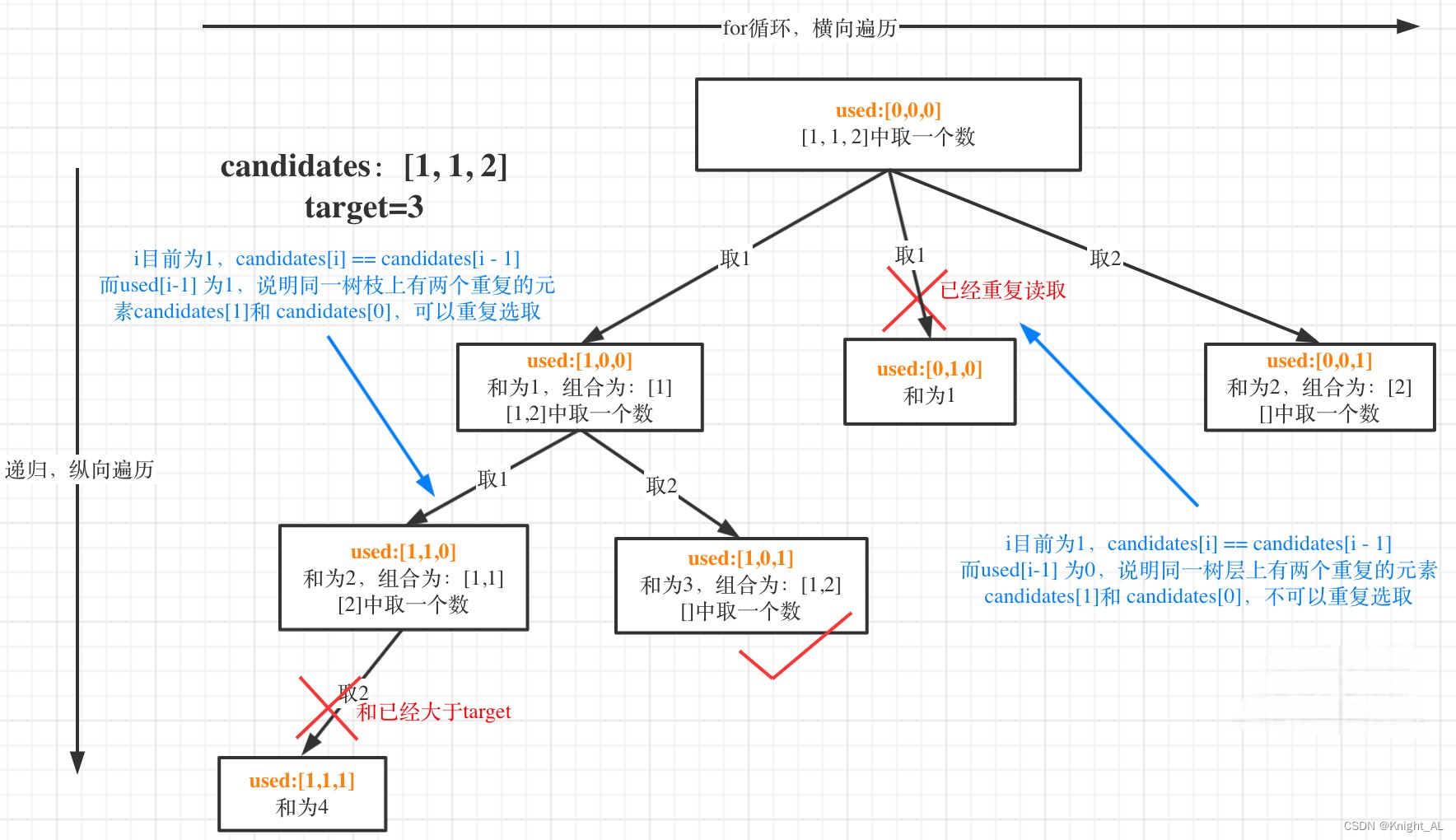
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
used[i - 1] == false,说明同一树层candidates[i - 1]使用过
为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
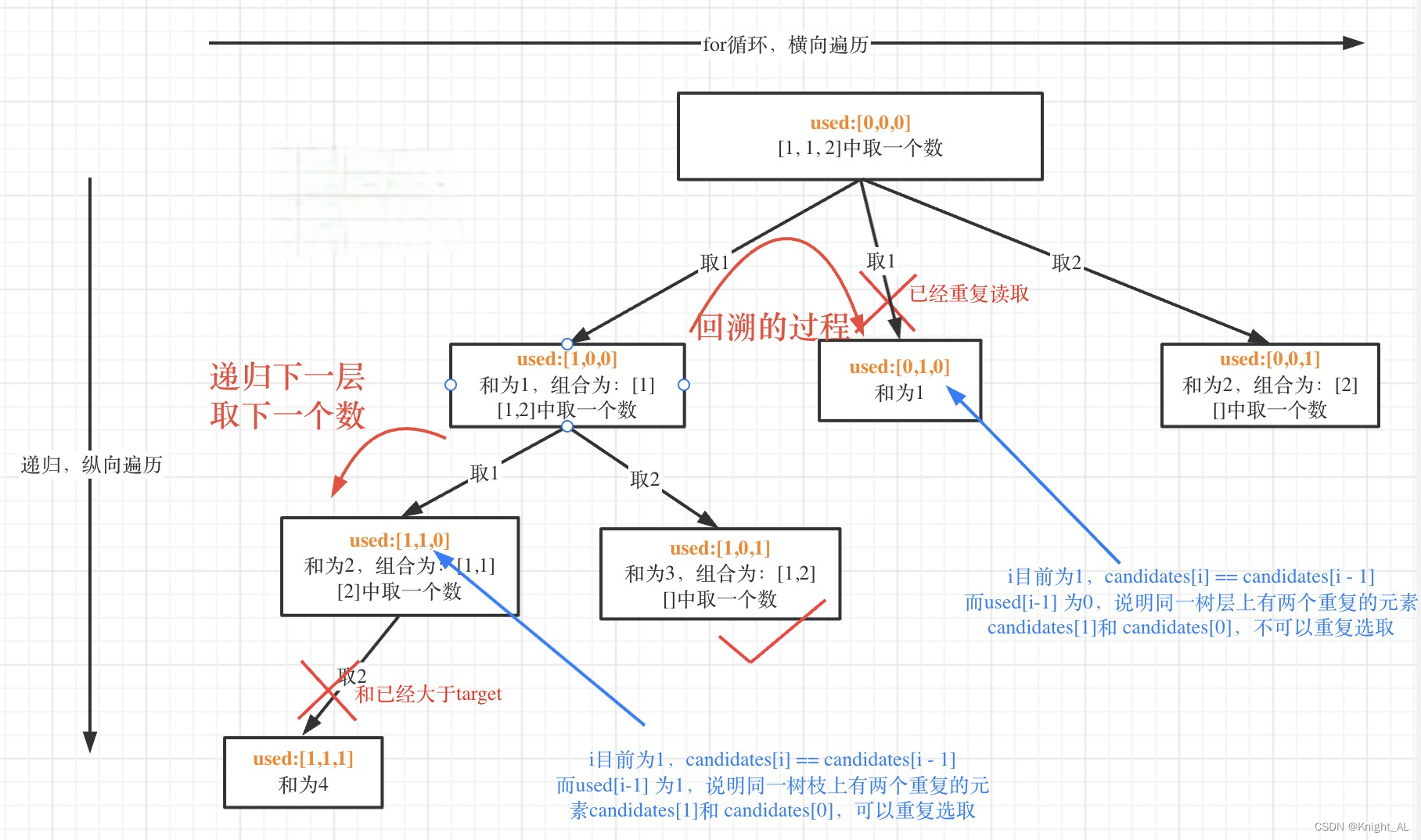
那么单层搜索的逻辑代码如下:
for(int i = startIndex;i<candidates.length && sum + candidates[i] <= target;i++){
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if(i>0 && candidates[i] == candidates[i-1] && !used[i-1]){
continue;
}
path.add(candidates[i]);
sum += candidates[i];
used[i] = true;
backtracking(candidates,target,sum,i+1,used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次
path.remove(path.size()-1);
sum -= candidates[i];
used[i] = false;
}
整体代码
class Solution {
ArrayList<List<Integer>> result = new ArrayList<>(); // 存放组合集合
ArrayList<Integer> path = new ArrayList<>(); // 符合条件的组合
boolean[] used;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
if(candidates == null || candidates.length == 0){
return result;
}
used = new boolean[candidates.length];
// 首先把给candidates排序,让其相同的元素都挨在一起。
Arrays.sort(candidates);
backtracking(candidates,target,0,0,used);
return result;
}
public void backtracking(int[] candidates, int target,int sum,int startIndex,boolean[] used){
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex;i<candidates.length && sum + candidates[i] <= target;i++){
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if(i>0 && candidates[i] == candidates[i-1] && !used[i-1]){
continue;
}
path.add(candidates[i]);
sum += candidates[i];
used[i] = true;
backtracking(candidates,target,sum,i+1,used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次
path.remove(path.size()-1);
sum -= candidates[i];
used[i] = false;
}
}
}