有序表之红黑树

news2025/2/26 14:55:39

文章目录

  • 1、五个条件
  • 2、调整策略
    • 2.1 插入调整的情况
      • 2.1.1 情况一：插入节点是红色，其父节点也是红色
      • 2.1.2 情况二
      • 2.1.2 代码实现
    • 2.2 删除调整的情况
      • 2.2.1 情况一：双重黑节点的兄弟节点也是黑色，且其兄弟的两个孩子也是黑色
      • 2.2.2 情况二：双重黑节点的兄弟节点是黑色，兄弟节点存在红色的子节点
      • 2.2.3 情况三
      • 2.2.4 思考：双黑节点的兄弟节点如果是红色，怎么办
      • 2.2.5 代码实现
  • 3、总结
    • 3.1 平衡条件
    • 3.2 学习诀窍
    • 3.3 插入策略
    • 3.4 插入调整代码重点
    • 3.5 删除调整发生的前提
    • 3.6 删除调整
    • 3.7 删除调整代码重点

1、五个条件

  1. 每个节点非黑即红
  2. 根节点是黑色
  3. 叶节点(NIL)是黑色【虚拟空节点，并不是看得见的叶子节点】
  4. 如果一个节点是红色，则它的两个子节点都是黑色的
  5. 从根节点出发到所有叶节点的路径上，黑色节点数量相同

结合第4点和第5点，红黑树中最短的路径和最长的路径之间的关系是：最长路径 = 2 x 最短路径。

假设最短边有3个黑色节点，那么最长边就是黑红相间的节点（不包含NIL节点）：

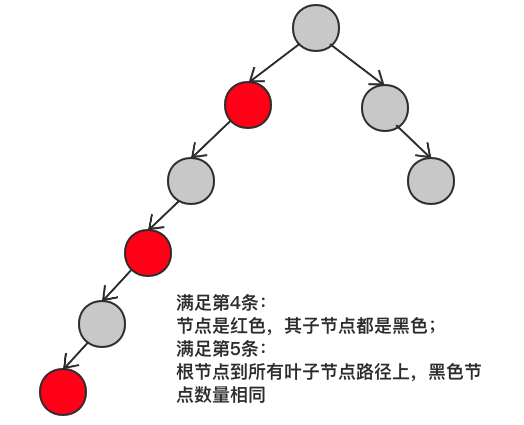
image-20201225222205202

如下左图所示的不是红黑树，因为其红色节点的子节点不是且黑色叶子节点不是黑色 ，而叶子节点并不是指的图中的1和18，而是右图所示的没有画出来的NIL结点：
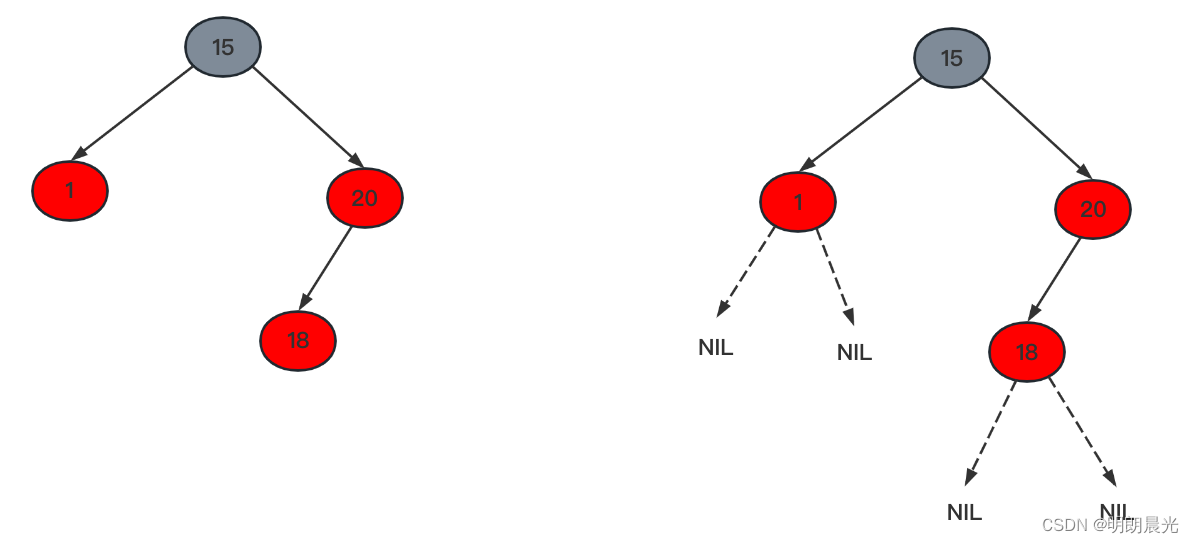
在这里插入图片描述
可见，红黑树的本质也是用树高控制平衡：最长路径 = 2 x 最短路径，但是相比AVL数控制得更松散一些，目的是不经常调整，减轻内存IO的消耗。

2、调整策略

  1. 插入调整站在 祖父节点 看
  2. 删除调整站在 父节点 看
  3. 插入和删除的情况处理一共 5 种

2.1 插入调整的情况

【分析】

  如果插入的节点是黑色的，那么就有一条路径上黑色节点的数量发生了改变，这个时候就需要进行调整。所以如果插入结点是黑色的，必然会调整。（即 插入黑色节点必然会调整）

  而插入红色节点，不会影响黑色节点的数量，如果红色节点插入到黑色节点下则不需要调整，如果插入到红色节点下，才需要调整。所以，插入红色节点可能会调整。（即 红色节点可能会调整）

  所以，红黑树在插入一个节点的时候，插入的节点必然是红色。

2.1.1 情况一：插入节点是红色，其父节点也是红色

x x x 为新插入的节点
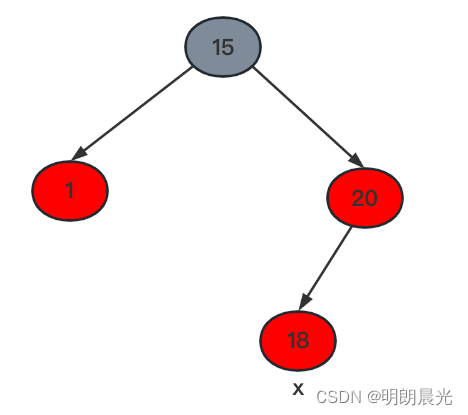
在这里插入图片描述
1）在插入操作回溯过程中，回溯到20节点发现冲突了，但是不要管它，继续往上回溯；回溯到15（祖父节点），向下看的时候发现20和18冲突，这个时候才进行调整。

2）将上图的这棵树看作一棵大的红黑树的子树。这部分 调整之前每条路径上的黑色节点数量 等于 调整之后每条路径上的黑色节点数量。即上图的这棵树，调整之前，每条路径上只有1个黑色节点，那么调整之后每条路径上也是1个黑色节点。之所以这么要求，就是为了不对红黑树的其他部分产生影响。这是一个通用的调整策略。【就算把15当做根节点，调整之后它是红色，那么最后一检查发现根节点不是黑色，将它变成黑色就行了】

3）当前(15, 1, 20)构成了 “黑-红-红” 的结构，这个“小帽子”，会给下面的子树每条路径提供一个黑色节点；但是还有一种红-黑-黑“小帽子”的情况，也会给子树每条路径提供一个黑色节点。这两种情况是等价的。（如下图所示的两种“小帽子”）
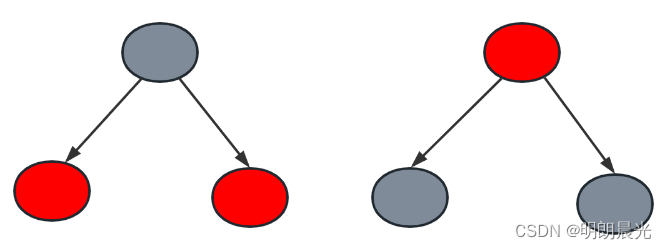
在这里插入图片描述

因此，情况一的调整方式：从祖父节点（黑色）向下看，两个子节点都是红色，并且孙子节点也有红色的时候，就将祖父节点改成红色，将它的两个孩子染成黑色（红-黑-黑)。

注意：之所以要将这棵树看作一棵大的红黑树的子树，是因为即便 15 变成了红色，就算它和它的父节点发生了冲突也是不处理的，而是要一直回溯到它的祖父节点才进行处理，这个过程是动态的。

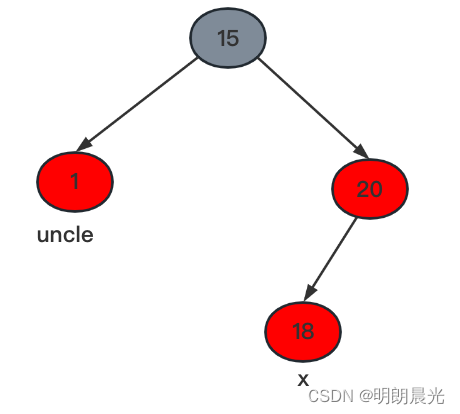
在这里插入图片描述
针对该样例的处理办法：1 和 20 修改成黑色，15 修改为红色（所谓红色上顶）。

情况一包含了 4 种小情况：插入的 x x x 是 1 的左节点或右节点、是 20 的左节点或右节点。

2.1.2 情况二

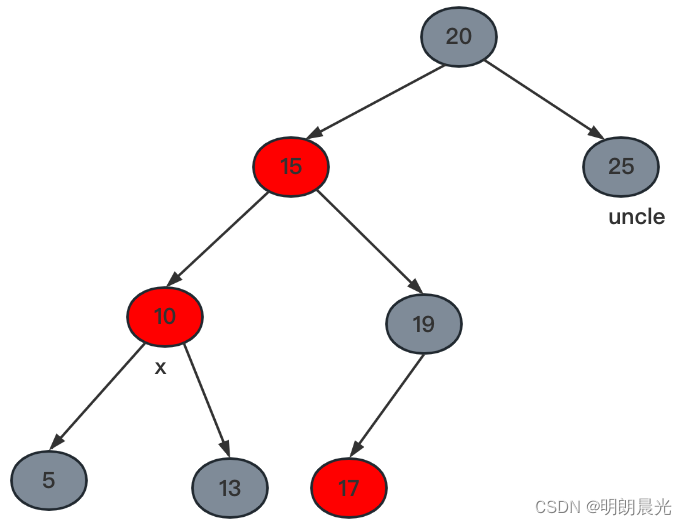
在这里插入图片描述
这种情况就是：祖父节点来看，它的左孩子是红色，左孩子的左孩子也是红色，但是右孩子为黑色。

从祖父节点(20)来看，它的左孩子是红色，左孩子的左孩子也是红色，就类似于AVL树中的LL类型失衡。

当发生LL失衡的时候，可以确定[20, 15, 10, 5, 13, 19, 25]都是确定的点以及就是图中的颜色，而17这个节点的颜色是不确定的。【将10号节点想象为（10，5，13)调整完后变成了红色，不然不好理解插入10不平衡的情况下它还有子节点】

抓着失衡节点20进行右旋得到如图：
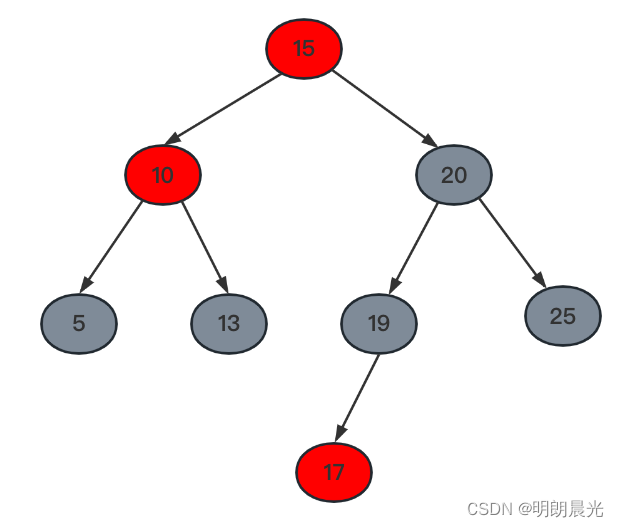
在这里插入图片描述
红黑树的调整原则：调整前每条路径上的黑色节点数量 = 调整后每条路径上的黑色节点数量

调整前，每条路径上的黑色节点数量为 2 个，则调整后每条路径上的黑色节点数量也是 2 个。而现在右旋后 [5, 13, 19, 25] 都是确定的黑色，也就是说需要在[15, 10, 20] 这个”小帽子“ 中再提供一个黑色节点，即是将当前的"小帽子"改成要么是 黑-红-红，要么是 红-黑-黑。

根节点改成红色叫做红色上浮（红-黑-黑），改成黑色叫做红色下沉（黑-红-红）。

总结来说，对于情况二，即LL类型失衡有两种调整策略：
  ① 先进行大右旋，然后将 “小帽子” 改成 黑-红-红 的结构；
  ② 先进行大右旋，然后将 “小帽子” 改成 红-黑-黑 的结构；

针对给出的样例，其中一种处理办法：大右（左）旋，20 调整成红色，15 调整成黑色，即可搞定问题。

对于LR类型失衡：先进行小左旋，转换为LL类型失衡，然后进行大右旋，最后调整颜色。（注：在小左旋的时候并不会改变子树上黑色节点数量的改变）

基于AVL中的平衡调整，RR类型失衡和RL类型失衡也可以类似进行处理。

2.1.2 代码实现

#include <stdio.h>
#include <stdlib.h>

//只包含红黑树的insert操作

typedef struct Node {
    int key;
    int color;//0 red, 1 black, 2 double black
    struct Node *lchild, *rchild;
} Node;

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL() {
    NIL->key = 0;
    NIL->color = 1;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}
//节点初始化
Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->color = 0;
    p->lchild = p->rchild = NIL;
    return p;
}

int has_red_child(Node *root) {
    return root->lchild->color == 0 || root->rchild->color == 0;
}

Node *left_rotate(Node *root) {
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    return temp;
}

Node *right_rotate(Node *root) {
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    return temp;
}

Node *insert_maintain(Node *root) {
    //当前节点没有红色子孩子，不会发生冲突，不需要做任何调整
    if (!has_red_child(root)) return root;
    //判断双红的情况：冲突发生在哪棵子树
    int flag = 0;
    //如果左右孩子都为红色，直接修改为红黑黑。处理插入情况1。
    //即便不发生冲突，这样修改也没有影响
    //这是一种偷懒的做法，因为没有判断是否发生了冲突
    if (root->lchild->color == 0 && root->rchild->color == 0) {
        //root->color = 0;
        //root->lchild->color = root->rchild->color = 1;
        //return root;
        goto insert_end;
    }
    //左孩子为红色，且左孩子的左孩子/右孩子也是红色（左子树发生了冲突）
    if (root->lchild->color == 0 && has_red_child(root->lchild)) flag = 1;
    //右孩子为红色，且右孩子的左孩子/右孩子也是红色（右子树发生了冲突）
    if (root->rchild->color == 0 && has_red_child(root->rchild)) flag = 2;
    //flag = 0表示没有发生冲突
    if (flag == 0) return root;
    if (flag == 1) {//L开头的失衡
        //判断是否为LR型，LR型需要先小左旋
        if (root->lchild->rchild->color == 0) {
            root->lchild = left_rotate(root->lchild);
        }
        root = right_rotate(root);
    } else { //R开头的失衡
        if (root->rchild->lchild->color == 0) {
            root->rchild = right_rotate(root->rchild);
        }
        root = left_rotate(root);
    }
insert_end:
    //修改三元组小帽子的颜色(可以红色上浮或红色下沉的改法)
    //此处使用的是红色上浮的改法：红-黑-黑
    root->color = 0;
    root->lchild->color = root->rchild->color = 1;
    return root;
}

//插入操作
Node *__insert(Node *root, int key) {
    if (root == NIL) return getNewNode(key);
    if (root->key == key) return root;
    if (key < root->key) {
        root->lchild = __insert(root->lchild, key);
    } else {
        root->rchild = __insert(root->rchild, key);
    }
    //回溯过程中进行插入调整
    return insert_maintain(root);
}

//给根节点染头为黑色，修改根节点的颜色为黑色,这是真正的根节点，如果是由红色变成黑色会给每条路径都增加一个黑色节点
//此处是调整解决冲突后的整棵树的根  
Node *insert(Node *root, int key) {
    root = __insert(root, key);
    root->color = 1;
    return root;
}

//销毁操作
void clear(Node *root) {
    if (root == NIL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

void print(Node *root) {
    printf("(%d| %d, %d %d)\n", root->color, root->key, root->lchild->key, root->rchild->key);
    return ;
}

void output(Node *root) {
    if (root == NIL) return ;
    print(root);
    output(root->lchild);
    output(root->rchild);
    return ;
}

int main() {
    int op, val;
    Node *root = NIL;
    while (~scanf("%d%d", &op, &val)) {
        switch (op) {
            case 1: root = insert(root, val); break;
        }
        output(root);
        printf("------------\n");
    }
    return 0;
}

运行测试：依次插入1，2，3

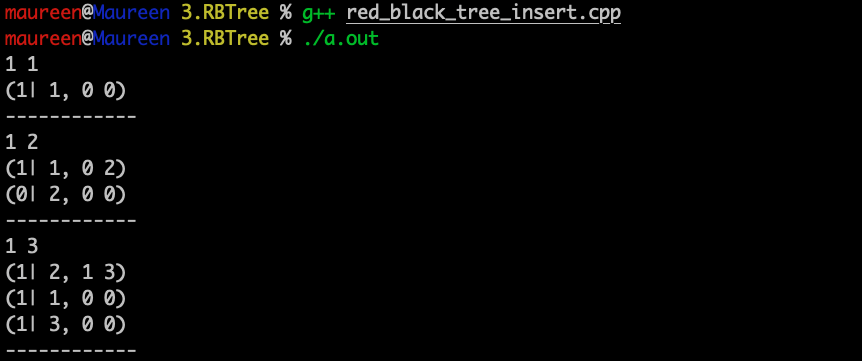
image-20201226161622493

输出结果的意义：(根节点颜色| 根节点值，左孩子值，右孩子值)

结果说明：当插入1和2之后，根节点为1，黑色；2为右孩子，红色；再插入3的时候，从1看来，出现了冲突，是RR型冲突，进行左旋，根节点就变成了2(红色），左孩子为1（黑色），右孩子为3(红色)，因为代码中采用的调整策略是红色上浮，这个三元组会被修改为 红-黑-黑 结构，即 3 被修改为黑色，但是因为 2 是根节点，会强制将其修改为黑色，于是三个节点都变成了黑色。2是真正的根节点，并非局部根节点，它从红色变成黑色，会给每条路径上都增加一个黑色节点，但是因为它是根节点，所以每条路径上的黑色节点的数量还是相同的。

2.2 删除调整的情况

【分析】

删除红色节点，不会对红黑树的平衡产生影响；删除黑色节点会对红黑树平衡产生影响。

而删除黑色节点又分为三种情况：删除的度为0、1、2的节点。而删除度为2的节点可以转换为删除度为0或1的节点，所以只需要讨论两种情况即可：

  • 删除的黑色节点是度为1的节点

例如下图所示，如果 x x x 为要删除的度为 1 的黑色节点，那么它的子节点一定为红色，因为以 x x x 为根节点的两棵子树的黑色节点数量要相同，现在 x x x 节点没有左子树，为了维持两棵子树的黑色节点数量相同都为0，所以 x x x 的右节点一定是红色。

即：删除的度为1的节点的子孩子一定是红色的
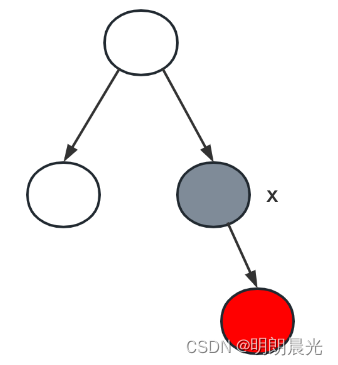
在这里插入图片描述
为了保证调整前后的黑色节点数量不变，所以删除黑色节点 x x x 后，将其子孩子挂到父节点上，并且将子孩子变成黑色。即是将删除的结点 x x x 的颜色加到唯一子孩子上。

  • 删除的黑色节点是度为0的节点

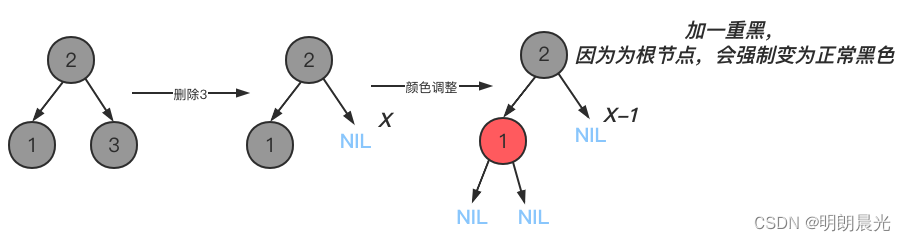
这种情况下就要使用到了 NIL 节点。如下左图所示，算上NIL节点，每条路径上 2 个黑色节点。但是当删除黑色节点后，取而代之的是一个新的 NIL 节点 NIL'(NIL'节点是个特殊的节点，被标记为黑色，但是它不是真实存在的节点），所以删除后每条路径上也要保证两个黑色节点，而 NIL'节点本身就是黑色，此时要做一个操作，将它标记为双重黑，才能保证每条路径上是两个黑色节点。也就是说将原来节点的黑色加到 NIL' 节点上，使得 NIL' 节点变成双重黑。
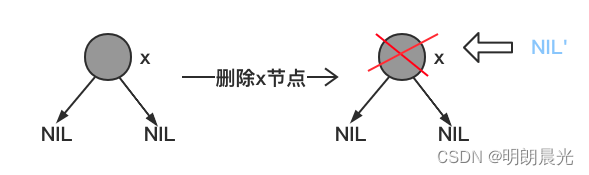
在这里插入图片描述在这里插入图片描述
另一个关于"双重黑" 的解释图例：
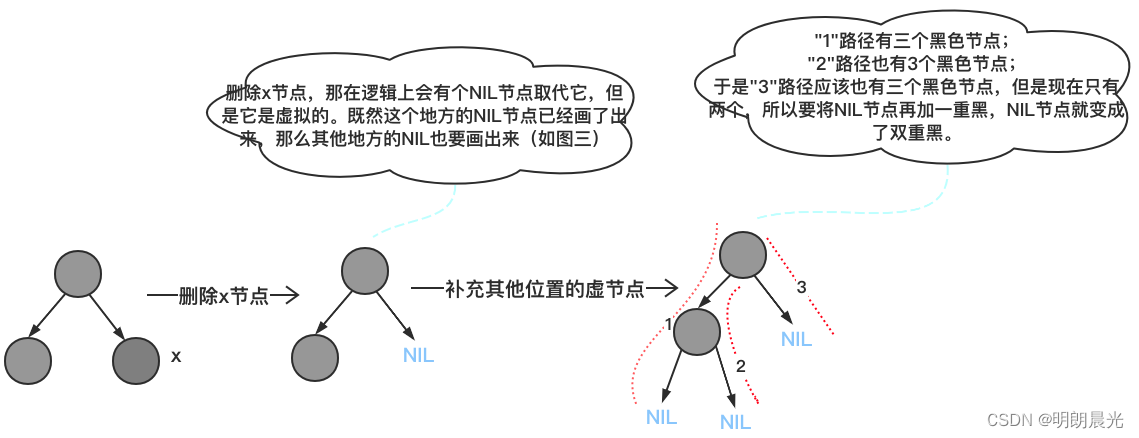
在这里插入图片描述
随着后续删除，这个双重黑的标记可能向上传递。

【结论】删除调整是为了干掉双重黑节点

2.2.1 情况一：双重黑节点的兄弟节点也是黑色，且其兄弟的两个孩子也是黑色

处理办法：

将双重黑的标记标记到父节点上(父节点加一重黑)，父节点的两个子孩子各减一重黑，双重黑节点就变成正常黑，兄弟节点就变成红色。

下图中标记为 x x x 的节点就是双重黑节点，站在父节点(43)向下看，看到一个双重黑的节点，需要进行删除调整。
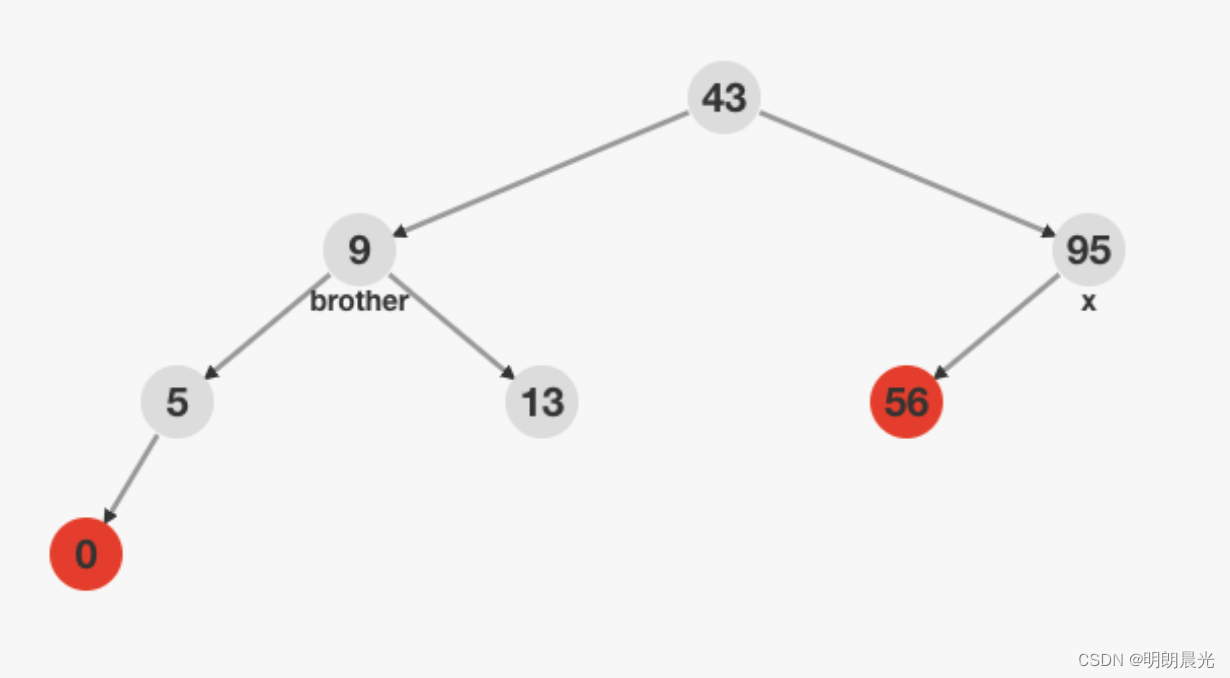
在这里插入图片描述
处理办法：brother 调整为红色， x x x 减少一重黑色，father 增加一重黑色。

2.2.2 情况二：双重黑节点的兄弟节点是黑色，兄弟节点存在红色的子节点

这种情况根据AVL失衡的情况进行划分：

1、兄弟节点在右侧，且兄弟节点的左侧是红色节点，兄弟节点的右子树一定是黑色，这种情况叫做RL

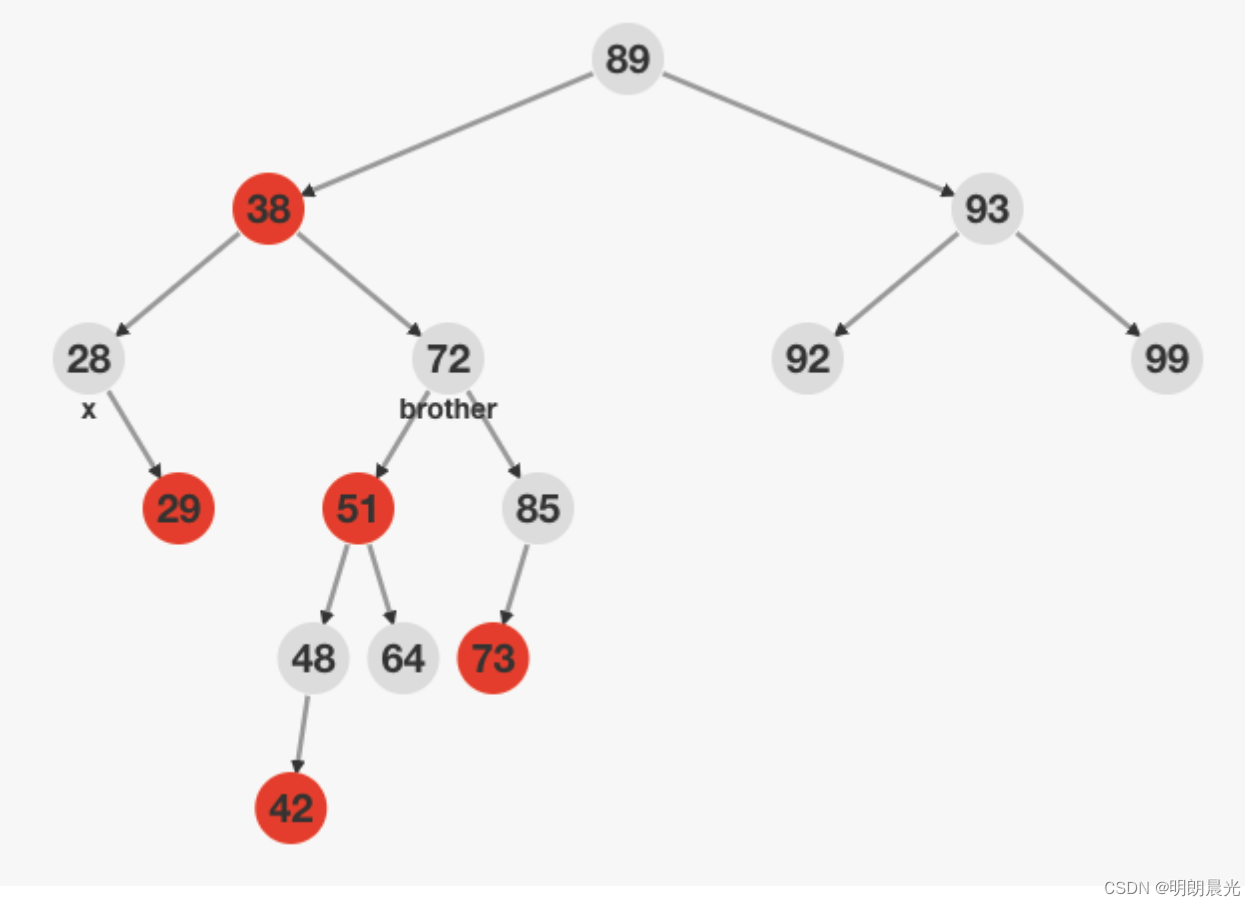
在这里插入图片描述

处理办法：右子树小右旋，转换为RR类型，抓着父节点进行大左旋。

子树 72 小右旋后的结果：
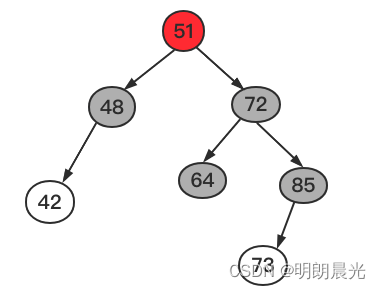
在这里插入图片描述
图中42和73的节点颜色是不确定的。旋转前，每棵子树上的黑色节点个数为2，旋转后经过颜色调整每棵子树上的黑色节点数量依然要为2。所以进行的颜色调整为：51变为黑色，72变为红色（因为64和85颜色是确定的黑色)。结合父节点38，就变成了RR类型。

2、兄弟节点在右侧，且兄弟节点的右侧是红色节点，无论兄弟节点的左侧节点是什么颜色，这种情况叫做RR，即情况三。

处理办法：抓住父节点左旋，然后修改颜色。

下图中，如果85是红色，就是RR类型，这种情况不管51的颜色。

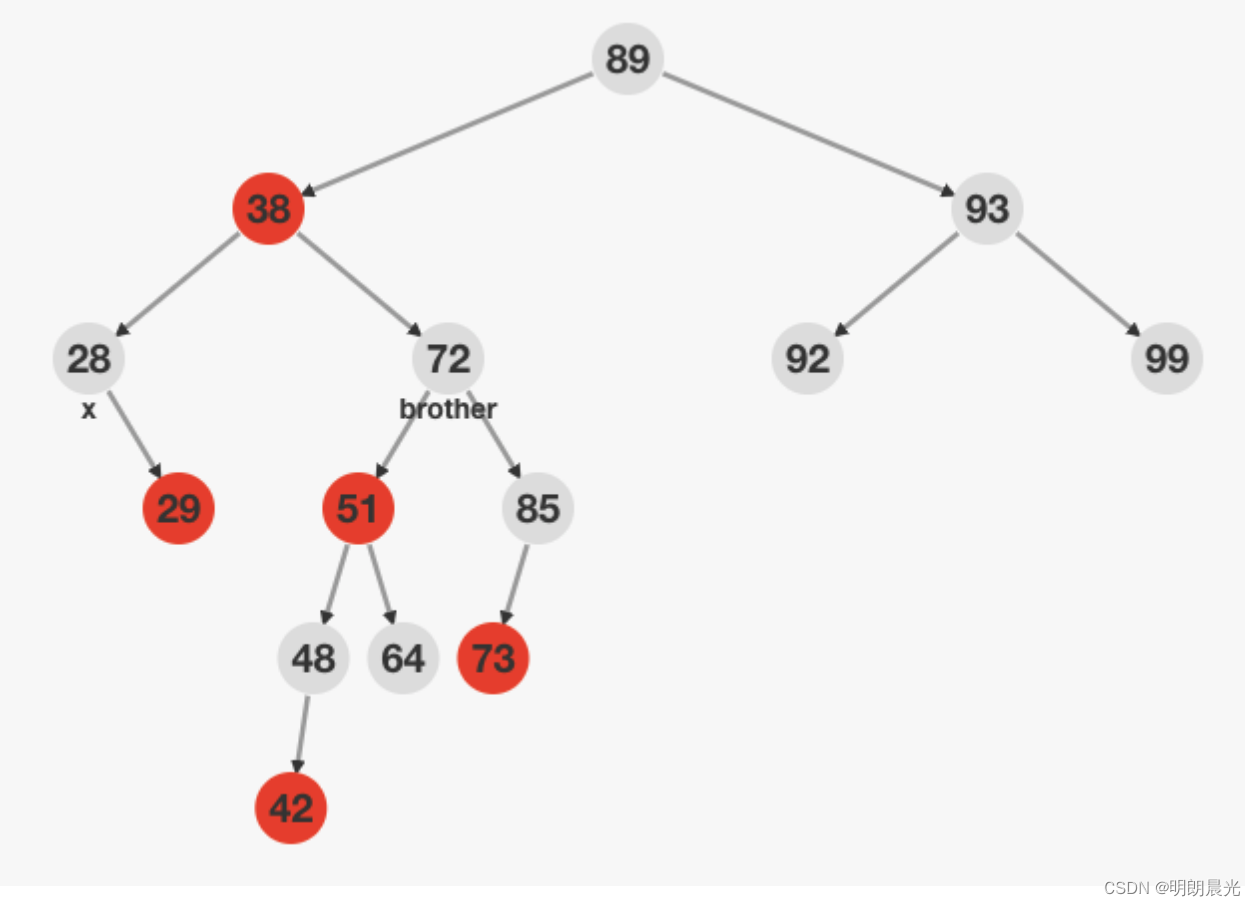
在这里插入图片描述
处理办法：brother 右(左)旋， 51 变黑， 72 变红，转成处理情况三

2.2.3 情况三

双重黑节点的兄弟节点在右子树且是黑色，且兄弟节点的右子树为红色(和兄弟节点在同一侧的，即兄弟节点在右子树上，兄弟节点的右子树上的节点是红色）， 这种情况叫做RR。

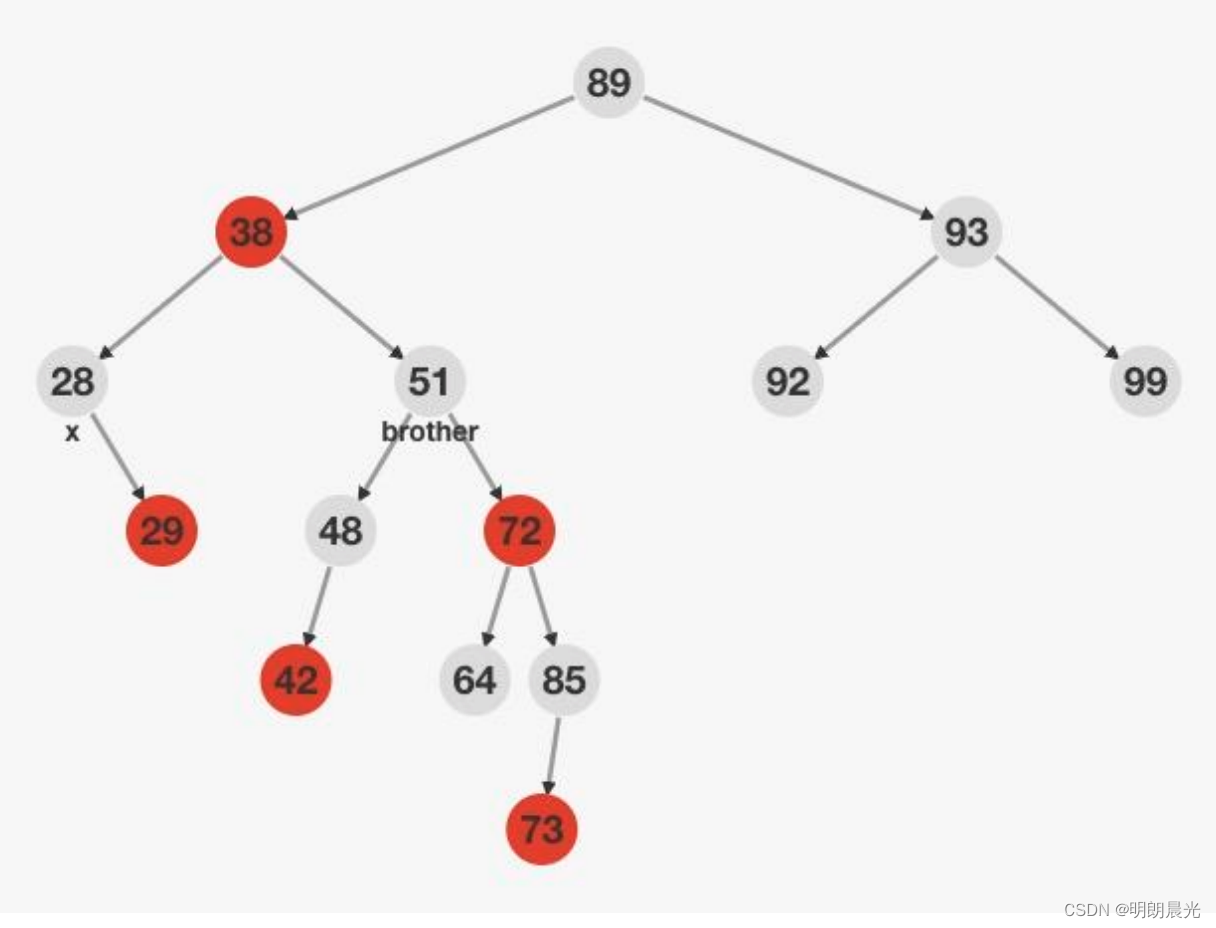
在这里插入图片描述
RR类型，抓着38节点进行左旋得到如下图所示：其中48节点的颜色是不确定。
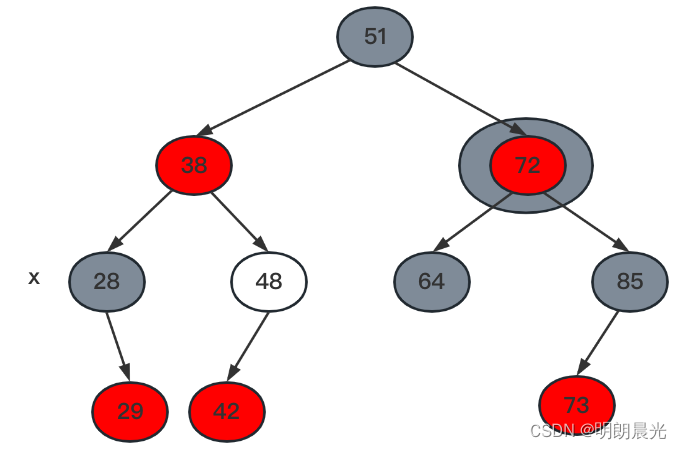
在这里插入图片描述
删除调整就是针对这棵经过左旋得到的树进行颜色修改，使得每棵子树旋转前后的黑色节点数量都为2。

修改颜色的思考过程：

因为48节点颜色不确定，如果48是红色，为了不发生冲突，只能将38改为黑色；又因为旋转前每条路径上是2个黑色节点，38一旦改成黑色，那么[51,38,28]这条路径上就变成了3个黑色节点，所以只能将51改成红色；而右侧每条路径上就变成了一个黑色节点，于是要将72改成黑色节点。

于是修改方法：51改成红色，38和72改成黑色。

但是这样修改有bug，如果38原来是黑色，那么51就得修改为红色，才能保证每条路径上两个黑色节点。

RR类型的修改方法：

双黑节点的父节点先大左旋，然后将左旋后的根节点颜色修改为原根节点的颜色，再把此时的子节点修改为黑色。

样例处理办法：father(38节点) 左(右)旋，由于无法确定 48 的颜色，所以38改成黑色， 51改成原38的颜色，x 减少一重黑色， 72改成黑色。

同理LL类型的调整策略类似。

2.2.4 思考：双黑节点的兄弟节点如果是红色，怎么办

如图，构建了一棵双黑节点的兄弟节点是红色的情况：

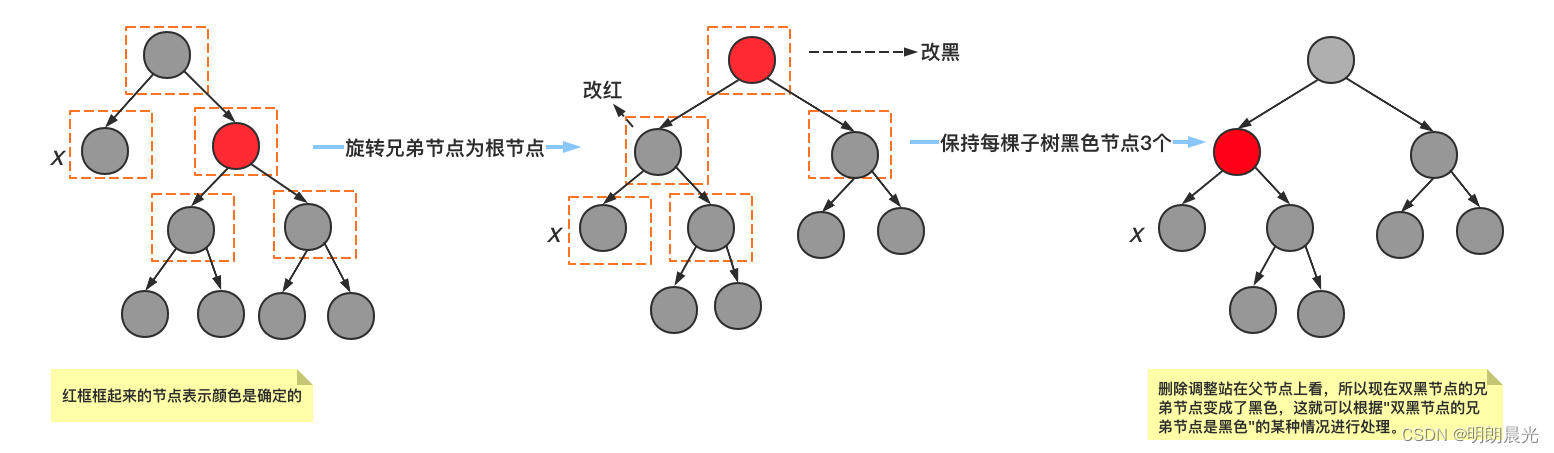
在这里插入图片描述
将其兄弟节点通过旋转成根节点，然后修改颜色，调整为双重黑节点的兄弟的节点为黑色的情况进行处理。

2.2.5 代码实现

//red_black_tree.cpp
#include <stdio.h>
#include <stdlib.h>
//包含红黑树的insert/erase操作
//完整版红黑树
typedef struct Node {
    int key;
    int color;//0 red, 1 black, 2 double black
    struct Node *lchild, *rchild;
} Node;

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void init_NIL() {
    NIL->key = 0;
    NIL->color = 1;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}
//节点初始化
Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->color = 0;
    p->lchild = p->rchild = NIL;
    return p;
}

int has_red_child(Node *root) {
    return root->lchild->color == 0 || root->rchild->color == 0;
}

Node *left_rotate(Node *root) {
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    return temp;
}

Node *right_rotate(Node *root) {
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    return temp;
}

Node *insert_maintain(Node *root) {
    //当前节点没有红色子孩子，不会发生冲突，不需要做任何调整
    if (!has_red_child(root)) return root;
    //判断双红的情况：冲突发生在哪棵子树
    int flag = 0;
    //如果左右孩子都为红色，直接修改为红黑黑。处理插入情况1。
    //即便不发生冲突，这样修改也没有影响
    //这是一种偷懒的做法，因为没有判断是否发生了冲突
    if (root->lchild->color == 0 && root->rchild->color == 0) {
        //root->color = 0;
        //root->lchild->color = root->rchild->color = 1;
        //return root;
        goto insert_end;
    }
    //左孩子为红色，且左孩子的左孩子/右孩子也是红色（左子树发生了冲突）
    if (root->lchild->color == 0 && has_red_child(root->lchild)) flag = 1;
    //右孩子为红色，且右孩子的左孩子/右孩子也是红色（右子树发生了冲突）
    if (root->rchild->color == 0 && has_red_child(root->rchild)) flag = 2;
    //flag = 0表示没有发生冲突
    if (flag == 0) return root;
    if (flag == 1) {//L开头的失衡
        //判断是否为LR型，LR型需要先小左旋
        if (root->lchild->rchild->color == 0) {
            root->lchild = left_rotate(root->lchild);
        }
        root = right_rotate(root);
    } else { //R开头的失衡
        if (root->rchild->lchild->color == 0) {
            root->rchild = right_rotate(root->rchild);
        }
        root = left_rotate(root);
    }
insert_end:
    //修改三元组小帽子的颜色(可以红色上浮或红色下沉的改法)
    //此处使用的是红色上浮的改法：红-黑-黑
    root->color = 0;
    root->lchild->color = root->rchild->color = 1;
    return root;
}

//插入操作
Node *__insert(Node *root, int key) {
    if (root == NIL) return getNewNode(key);
    if (root->key == key) return root;
    if (key < root->key) {
        root->lchild = __insert(root->lchild, key);
    } else {
        root->rchild = __insert(root->rchild, key);
    }
    //回溯过程中进行插入调整
    return insert_maintain(root);
}

//修改根节点的颜色为黑色
Node *insert(Node *root, int key) {
    root = __insert(root, key);
    root->color = 1;
    return root;
}

Node *predecessor(Node *root) {
    Node *temp = root->lchild;
    while (temp->rchild != NIL) temp = temp->rchild;
    return temp;
}

Node *erase_maintain(Node *root) {
    //删除节点站在父节点
    //左右节点都不是双重黑，不用调整
    if (root->lchild->color != 2 && root->rchild->color != 2) return root;
    //有双重黑节点且兄弟节点是红色
    if (has_red_child(root)) {
        int flag = 0;
        //原根节点给成红色
        root->color = 0;
        //将红色节点通过旋转成为根节点
        if (root->lchild->color == 0) {
            root = right_rotate(root);
            flag = 1;
        } else {
            root = left_rotate(root);
            flag = 2;
        }
        //新根节点改成黑色
        root->color = 1;
        //转换为兄弟节点是黑色的情况进行处理
        if (flag == 1) root->rchild = erase_maintain(root->rchild);
        else root->lchild = erase_maintain(root->lchild);
        return root;
    }
    //处理情况一：
    //兄弟节点在右侧且兄弟节点没有红色子孩子
    //兄弟节点在左侧且兄弟节点没有红色子孩子
    if ((root->lchild->color == 2 && !has_red_child(root->rchild)) ||
        (root->rchild->color == 2 && !has_red_child(root->lchild))) {
        root->lchild->color -= 1;
        root->rchild->color -= 1;
        root->color += 1;
        return root;
    }
    if (root->lchild->color == 2) {
        root->lchild->color = 1;
        //右侧的兄弟节点的右节点颜色不为红色，若为红色就是RR，不需要进行小右旋
        //不能用root->rchild->rchild->color == 1,因为可能为NIL节点，可能是双重黑
        if (root->rchild->rchild->color != 0) {//RL
            //原根颜色变为红色
            root->rchild->color = 0;
            root->rchild = right_rotate(root->rchild);
            //新根颜色变为黑色
            root->rchild->color = 1;

        }
        root = left_rotate(root);
        root->color = root->lchild->color;
    } else {
        root->rchild->color = 1;
        if (root->lchild->lchild->color != 0) { //LR
            root->lchild->color = 0;
            root->lchild = left_rotate(root->lchild);
            root->lchild->color = 1;
        }
        root = right_rotate(root);
        root->color = root->rchild->color;
    }
    root->lchild->color = root->rchild->color = 1;
    return root;
}

Node *__erase(Node *root, int key) {
    if (root == NIL) return NIL;
    if (key < root->key) {
        root->lchild = __erase(root->lchild, key);
    } else if (key > root->key) {
        root->rchild = __erase(root->rchild, key);
    } else {
        //删除度为0或1的节点
        if (root->lchild == NIL || root->rchild == NIL) {
            Node *temp = root->lchild != NIL ? root->lchild : root->rchild;
            //将当前节点颜色加到唯一子孩子上
            //如果root为红色，对子孩子颜色没有影响；
            //如果root为黑色，就要将这个颜色加到唯一子孩子上
            temp->color += root->color;
            free(root);
            return temp;
        } else { //删除度为2的节点
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = __erase(root->lchild, temp->key);
        }
    }
    return erase_maintain(root);
}

Node *erase(Node *root, int key) {
    root = __erase(root, key);
    root->color = 1;
    return root;
}

//销毁操作
void clear(Node *root) {
    if (root == NIL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

void print(Node *root) {
    printf("(%d| %d, %d %d)\n", root->color, root->key, root->lchild->key, root->rchild->key);
    return ;
}

void output(Node *root) {
    if (root == NIL) return ;
    print(root);
    output(root->lchild);
    output(root->rchild);
    return ;
}

int main() {
    int op, val;
    Node *root = NIL;
    while (~scanf("%d%d", &op, &val)) {
        switch (op) {
            case 1: root = insert(root, val); break;
            case 2: root = erase(root, val); break;
        }
        output(root);
        printf("------------\n");
    }
    return 0;
}

运行测试1：
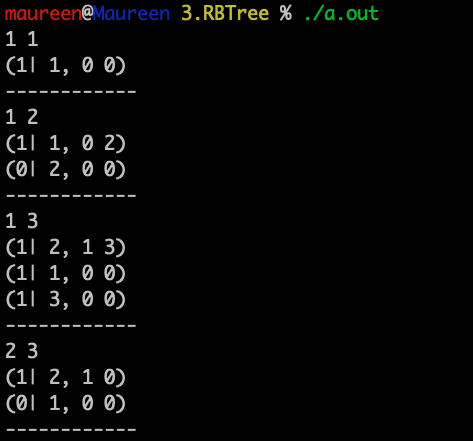
image-20201228173037623
结果分析：这就是兄弟节点为黑色，且兄弟节点的两个子节点都为黑色，处理方案就是将父节点加一重黑，子节点各减一重黑，所以兄弟那个节点就变为红色，此处即是1变为红色。而父节点此时是根节点，所以会被强制变为正常黑。
在这里插入图片描述
运行测试2：
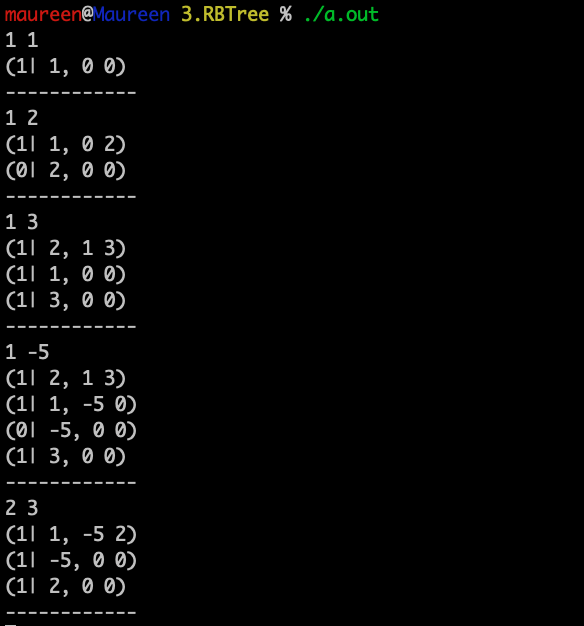
image-20201228174119553
结果分析：删除3节点后，用NIL节点替代3，且被标记为双重黑；其兄弟节点在左侧为黑色，且兄弟节点的左孩子为红色，就是LL类型，所以进行大右旋。右旋之后，将新根节点修改为原根节点的颜色；新根节点的孩子节点修改为黑色。

3、总结

3.1 平衡条件

  1. 节点非黑即红
  2. 根节点是黑色
  3. 叶子(NIL) 结点是黑色
  4. 红色节点下面接两个黑色节点
  5. 从根节点到叶子节点路径上，黑色节点数量相同

平衡条件的认识

第4和5条注定了红黑树中最长路径是最短路径的2倍。

本质上，红黑树也是通过树高来控制平衡的。

红黑树比AVL树树高控制条件要更松散，红黑树在发生节点插入和删除以后，发生调整的概率，比AVL树要更小。

3.2 学习诀窍

  1. 理解红黑树的插入调整，要站在 祖父节点 向下进行调整
  2. 理解红黑树的删除调整，要站在 父节点 向下进行调整
  3. 插入调整，主要就是为了解决双红情况
  4. 新插入的节点一定是红色。插入黑色节点一定会产生冲突，违反条件5；插入红色节点，不一定产生冲突
  5. 把每一种情况，想象成一棵大的红黑树中的局部子树
  6. 局部调整的时候，为了不影响全局，调整前后每条路径上黑色节点的数量相同

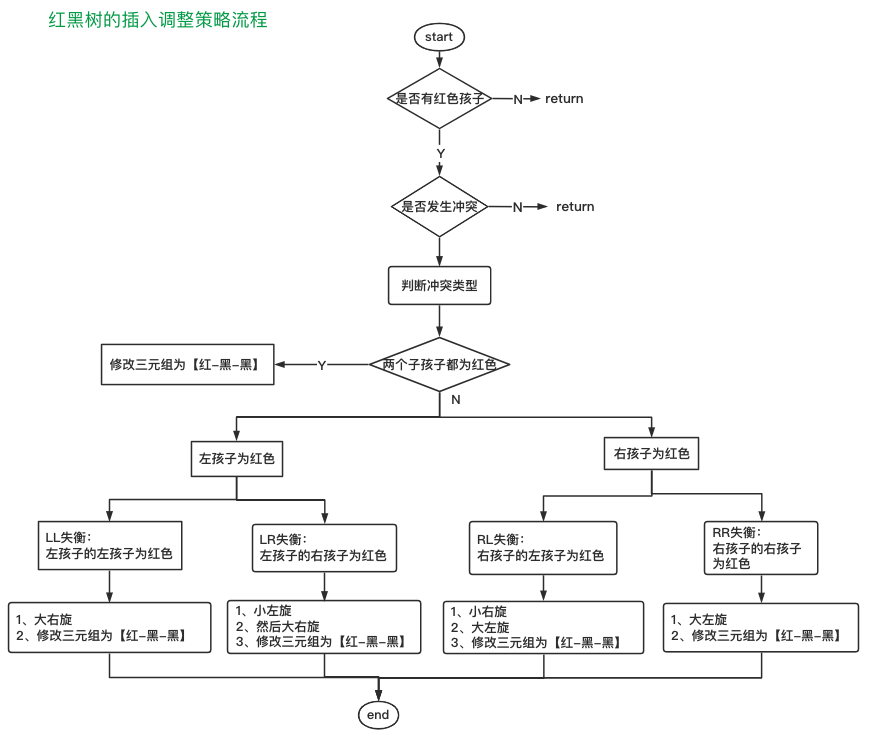
3.3 插入策略

  1. 叔叔节点为红色的时候，修改三元组小帽子，改成红黑黑
  2. 叔叔节点为黑色的时候，参考AVL树的失衡情况，分成 LL，LR，RL，RR，先参考AVL树的旋转调整策略，然后再修改三元组的颜色，有两种调整策略：红色上浮，红色下沉。
  3. 两大类情况，包含8种小情况

image-20210221140717026

3.4 插入调整代码重点

  1. 插入调整，发生在递归的回溯阶段
  2. 插入调整代码中，使用 goto 语句，8行代码变成了4行
  3. 处理根节点一定是黑色，通过代码封装，insert->__insert

3.5 删除调整发生的前提

  1. 删除红色节点不会对红黑树的平衡产生影响
  2. 度为1的黑色节点，唯一子孩子一定是红色
  3. 删除度为1的黑色节点，不会产生删除调整
  4. 删除度为0的黑色节点，会产生一个双重黑的NIL节点
  5. 删除调整，就是为了干掉双重黑

3.6 删除调整

  1. 双重黑节点的兄弟节点是黑色，兄弟节点下面的两个子节点也是黑色，父节点增加一重黑色，双重黑与兄弟节点分别减少一重黑色。
  2. 双重黑节点的兄弟节点是黑色，并且，兄弟节点中有红色子节点
    1. R（兄弟）R（右子节点），左旋，新根改成原根的颜色，将新根的两个子节点改成黑色，双重黑节点改成一重黑；
    2. R（兄弟）L（左子节点），先小右旋，对调新根与原根的颜色，转成上一种情况；
    3. LL 同理 RR
    4. LR 同理 RL
  3. 双重黑节点的兄弟节点是红色，通过旋转，转变成兄弟节点是黑色的情况

在这里插入图片描述

3.7 删除调整代码重点

进行LR/RL类型判断的时候，不能判断 LL 子树是否为黑色，因为LL子树有可能是NIL节点，在某些特殊情况下，读到的颜色可能是双重黑，取而代之的判断方法是【LL子树不是红色】

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/361581.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

100亿级订单怎么调度，来一个大厂的极品方案

100亿级订单怎么调度，来一个大厂的极品方案

背景 超时处理&#xff0c;是一个很有技术难度的问题。 所以很多的小伙伴&#xff0c;在写简历的时候&#xff0c;喜欢把这个技术难题写在简历里边&#xff0c; 体现自己高超的技术水平。 在40岁老架构师 尼恩的读者交流群(50)中&#xff0c;尼恩经常指导大家 优化简历。 最…
阅读更多...
教你学git

教你学git

前言 git是一种用于多人合作写项目。详细说明如下 文章目录前言什么是版本控制&#xff1f;什么是 Git&#xff1f;它就属于人工版本控制器版本控制工具常见版本控制工具怎么工作的&#xff1f;git 文件生命周期状态区域安装配置-- global检查配置创建仓库工作流与基本操作查看…
阅读更多...
高精密数字源表的发展史

高精密数字源表的发展史

在半导体、汽车、医疗等高端制造行业&#xff0c;源表通常被用于半导体材料或精密器件的电性能特性测试和生产测试应用&#xff0c;以及中低电平测试和实验室研究使用。源表采用四象限工作模式&#xff0c;可以在提供精密电压、电流源的同时&#xff0c;又能够作为电压、电流、…
阅读更多...
浅谈Java线程池中的ThreadPoolExecutor工具类

浅谈Java线程池中的ThreadPoolExecutor工具类

目录 ThreadPoolExecutor的构造函数 关于线程池的一些补充 线程池运行原理分析 概念原理解释 整个流程图如下&#xff1a; 一点补充 创建线程池主要有两种方式&#xff1a; 通过Executor工厂类创建&#xff0c;创建方式比较简单&#xff0c;但是定制能力有限通过ThreadPoo…
阅读更多...
Git ---- 概述

Git ---- 概述

Git ---- 概述1. 何为版本控制2. 为什么需要版本控制3. 版本控制的工具集中式版本控制工具分布式版本控制工具4. Git 简史5. Git 工作机制6. Git 和代码托管中心Git 是一个免费的、开源的分布式版本控制系统&#xff0c;可以快速高效地处理从小型到大型的各种项目。 Git 易于学…
阅读更多...
深入浅出C++ ——继承

深入浅出C++ ——继承

文章目录一、继承的相关概念1. 继承的概念2. 继承格式3. 继承方式4. 访问限定符5. 继承基类成员访问方式的变化二、基类和派生类对象赋值转换三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员七、菱形继承及菱形虚拟继承1. 单继承2. 多继承3. 菱形…
阅读更多...
【比赛合集】9场可报名的「创新应用」、「程序设计」大奖赛，任君挑选！

【比赛合集】9场可报名的「创新应用」、「程序设计」大奖赛，任君挑选！

CompHub 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…&#xff09;比赛。本账号同时会推送最新的比赛消息&#xff0c;欢迎关注&#xff01;更多比赛信息见 CompHub主页 或 点击文末阅读原文以下信息仅供参考&#xff0c;以比赛官网为准目录创新应用赛&…
阅读更多...
基于Java+SpringBoot+Vue+Uniapp前后端分离健身预约系统设计与实现

基于Java+SpringBoot+Vue+Uniapp前后端分离健身预约系统设计与实现

博主介绍&#xff1a;✌全网粉丝3W&#xff0c;全栈开发工程师&#xff0c;从事多年软件开发&#xff0c;在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战✌ 博主作品&#xff1a;《微服务实战》专栏是本人的实战经验总结&#xff0c;《Spring家族及…
阅读更多...
linux集群技术（二）--keepalived（高可用集群）（一）

linux集群技术（二）--keepalived（高可用集群）（一）

高可用集群简介keepalived简介 1.高可用集群简介 1.1什么是高可用集群 高可用集群&#xff08;High Availability Cluster&#xff0c;简称HA Cluster&#xff09;&#xff0c;是指以减少服务中断时间为目的的服务器集群技术。它通过保护用户的业务程序对外不间断提供的服务&am…
阅读更多...
Vue3后台管理系统（一）基础环境

Vue3后台管理系统（一）基础环境

目录 一、初始化 二、整合Element-Plus 三、路径别名 四、多环境配置 五、反向代理 六、其他依赖 一、初始化 npm init vitelatest vue3-element-admin --template vue-ts 二、整合Element-Plus 1.本地安装Element Plus和图标组件 npm install element-plus npm inst…
阅读更多...
code-breaking之javacon

code-breaking之javacon

JAVACON 题目 此题 来自P神 的code-breaking中的一道Java题&#xff0c;名为javacon&#xff0c;题目知识点为SpEL注入 题目下载地址&#xff1a;https://www.leavesongs.com/media/attachment/2018/11/23/challenge-0.0.1-SNAPSHOT.jar 运行环境 java -jar challenge-0.…
阅读更多...
实用指南：如何在Anolis OS上轻松使用 Kata 安全容器？

实用指南：如何在Anolis OS上轻松使用 Kata 安全容器？

文/云原生SIG本篇文章我们将详细介绍怎么轻松在 Anolis OS 上使用 Kata Containers 安全容器&#xff0c;我们将介绍 Kata Container 社区于 2022 年 10 月 10 日最新发行的 Kata3.0.0 的安装部署方式&#xff0c;3.0.0 版本包含了基于袋鼠 RunD 开源的最新 Rust Kata runtime …
阅读更多...
AAAI 2023 | 小鹏汽车纽约石溪：在末层激活上作对抗训练的域自适应

AAAI 2023 | 小鹏汽车纽约石溪：在末层激活上作对抗训练的域自适应

原文链接&#xff1a;https://www.techbeat.net/article-info?id4602 作者&#xff1a;吕骋 增强未标记目标域数据的模型预测置信度是无监督域自适应&#xff08;UDA&#xff09; 的一个重要目标。在本文中&#xff0c;作者探讨了末层激活&#xff08;即最后一层线性分类层输入…
阅读更多...
以假乱真的手写模拟器？

以假乱真的手写模拟器？

前些时候给大家推荐了一款word插件叫做“不坑盒子”&#xff0c;这款盒子不仅方便了word的操作&#xff0c;还附带了手写模拟器这样的效果只是在使用的时候不仅需要手动下载字体&#xff0c;而且效果也并不是太理想。 今天小编找到了一款软件--手写模拟器&#xff0c;不仅一键生…
阅读更多...
木鱼cms系统审计小结

木鱼cms系统审计小结

MuYuCMS基于Thinkphp开发的一套轻量级开源内容管理系统,专注为公司企业、个人站长提供快速建站提供解决方案。 ​​ ‍ 环境搭建 我们利用 phpstudy 来搭建环境&#xff0c;选择 Apache2.4.39 MySQL5.7.26 php5.6.9 &#xff0c;同时利用 PhpStorm 来实现对项目的调试 ​…
阅读更多...
求数组中的第k小元素

求数组中的第k小元素

文章目录第k小的元素&#x1f512;题目&#x1f4a1;分析&#x1f511;题解&#x1f343;不去重版&#x1f343;去重版第k小的元素 &#x1f512;题目 题目来源&#xff1a;3533. 查找第K小数 - AcWing题库 &#x1f4a1;分析 不去重版思路&#xff1a;去重版思路&#xff1a…
阅读更多...
华为OD机试 - 斗地主（C++） | 附带编码思路 【2023】

华为OD机试 - 斗地主（C++） | 附带编码思路 【2023】

刷算法题之前必看 参加华为od机试，一定要注意不要完全背诵代码，需要理解之后模仿写出，通过率才会高。 华为 OD 清单查看地址：https://blog.csdn.net/hihell/category_12199283.html 华为OD详细说明：https://dream.blog.csdn.net/article/details/128980730 华为OD机试题…
阅读更多...
一、【cas搭建单点登录】使用cas搭建单点登录服务器

一、【cas搭建单点登录】使用cas搭建单点登录服务器

使用cas搭建单点登录服务器 环境要求 JDK 8CAS 5.2tomcat 8 选用5.x的cas版本是应为要是jdk1.8的版本。 cas版本jdk版本5.x86.x117.x17 模板下载 目前cas的官方文档中&#xff0c;cas官方模板分成了5个大类。cas-sso-server 模板下载地址。 在cas的官方模板库中&#xff…
阅读更多...
2023年2月22日PMP®项目管理认证课程正式开课

2023年2月22日PMP®项目管理认证课程正式开课

PMP认证是Project Management Institute在全球范围内推出的针对评价个人项目管理知识能力的资格认证体系。国内众多企业已把PMP认证定为项目经理人必须取得的重要资质。 PMP认证是Project Management Institute在全球范围内推出的针对评价个人项目管理知识能力的资格认证体系。…
阅读更多...
微服务之Eureka

微服务之Eureka

&#x1f3e0;个人主页&#xff1a;阿杰的博客 &#x1f4aa;个人简介&#xff1a;大家好&#xff0c;我是阿杰&#xff0c;一个正在努力让自己变得更好的男人&#x1f468; 目前状况&#x1f389;&#xff1a;24届毕业生&#xff0c;奋斗在找实习的路上&#x1f31f; &#x1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023