1、N 皇后（数组，回溯）

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

 

示例 1：

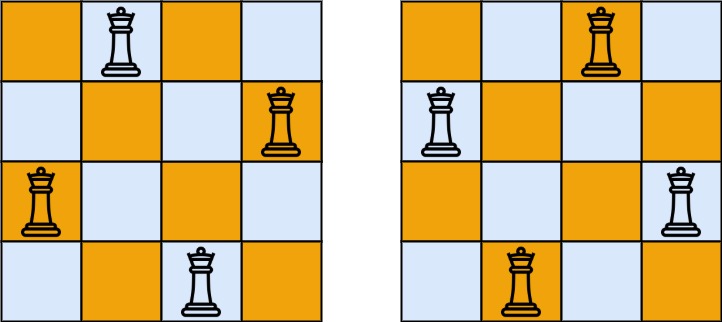
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

 

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

以下程序实现了这一功能，请你填补空白处内容：

class Solution(object):
	def solveNQueens(self, n):
		if n == 0:
			return 0
		res = []
		board = [['.'] * n for t in range(n)]
		self.do_solveNQueens(res, board, n)
		return res
	def do_solveNQueens(self, res, board, num):
		if num == 0:
			res.append([''.join(t) for t in board])
			return
		ls = len(board)
		pos = ls - num
		check = [True] * ls
		for i in range(pos):
			for j in range(ls):
				if board[i][j] == 'Q':
					______________________;
		for j in range(ls):
			if check[j]:
				board[pos][j] = 'Q'
				self.do_solveNQueens(res, board, num - 1)
				board[pos][j] = '.'
if __name__ == '__main__':
	s = Solution()
	print (s.solveNQueens(4))

选项代码：

                        check[j] = False
                        step = pos - i
                        if j + step < ls:
                            check[j + step] = False
                        if j - step >= 0:
                            check[j - step] = False
                        break

2、二叉树的前序遍历（栈，树）

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

 

示例 1：

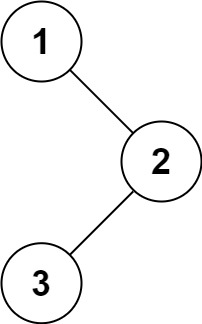
输入：root = [1,null,2,3] #这里输入应改为None，python中没有null

输出：[1,2,3]

示例 2：

输入：root = []

输出：[]

示例 3：

输入：root = [1]

输出：[1]

示例 4：

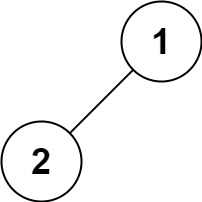
输入：root = [1,2]

输出：[1,2]

示例 5：

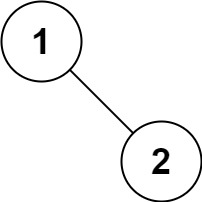
输入：root = [1,null,2]   #这里输入应改为None，python中没有null

输出：[1,2]

 

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

 

进阶：递归算法很简单，你可以通过迭代算法完成吗？

选项代码：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution:
    def __init__(self):
        self.ans = []

    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        self.ans.append(root.val)
        self.preorderTraversal(root.left)
        self.preorderTraversal(root.right)
        return self.ans

3、四数之和（数组，双指针）

给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

注意：答案中不可以包含重复的四元组。

 

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [], target = 0
输出：[]

 

提示：

• 0 <= nums.length <= 200
• -109 <= nums[i] <= 109
• -109 <= target <= 109

请在以下选项中选择

选项代码：

class Solution(object):
    def fourSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        nums.sort()
        results = []
        N = len(nums)
        i = 0
        while i < N-3:
            if i > 0 and nums[i] == nums[i-1]:
                i += 1
                continue
            j = i+1
            while j < N-2:
                if j > i+1 and nums[j] == nums[j-1]:
                    j += 1
                    continue
                k = j+1
                l = N-1
                while k < l:
                    if k > j+1 and nums[k] == nums[k-1]:
                        k += 1
                        continue
                    while k < l and (target - nums[i] - nums[j] - nums[k] - nums[l]) < 0:
                        l -= 1
                    if k >= l:
                        break
                    if target == nums[i] + nums[j] + nums[k] + nums[l]:
                        results.append([
                            nums[i],
                            nums[j],
                            nums[k],
                            nums[l]
                        ])
                    k += 1
                j += 1
            i += 1
        return results
# %%
s = Solution()
print(s.fourSum(nums = [1,0,-1,0,-2,2], target = 0))