K-近邻算法（KNN）

K nearest neighbour

0、导引

如何进行电影分类

众所周知，电影可以按照题材分类，然而题材本身是如何定义的?由谁来判定某部电影属于哪
个题材?也就是说同一题材的电影具有哪些公共特征?这些都是在进行电影分类时必须要考虑的问
题。没有哪个电影人会说自己制作的电影和以前的某部电影类似，但我们确实知道每部电影在风格
上的确有可能会和同题材的电影相近。那么动作片具有哪些共有特征，使得动作片之间非常类似，
而与爱情片存在着明显的差别呢？动作片中也会存在接吻镜头，爱情片中也会存在打斗场景，我们
不能单纯依靠是否存在打斗或者亲吻来判断影片的类型。但是爱情片中的亲吻镜头更多，动作片中
的打斗场景也更频繁，基于此类场景在某部电影中出现的次数可以用来进行电影分类。

本章介绍第一个机器学习算法：K-近邻算法，它非常有效而且易于掌握。

1、k-近邻算法原理

简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类。

• 优点：精度高、对异常值不敏感、无数据输入假定。
• 缺点：时间复杂度高、空间复杂度高。
• 适用数据范围：数值型和标称型。

工作原理

存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据
与所属分类的对应关系。输人没有标签的新数据后，将新数据的每个特征与样本集中数据对应的
特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们
只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处,通常K是不大于20的整数。
最后 ，选择K个最相似数据中出现次数最多的分类，作为新数据的分类。

回到前面电影分类的例子，使用K-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头，下图显示了6部电影的打斗和接吻次数。假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？我们可以使用K-近邻算法来解决这个问题。

首先我们需要知道这个未知电影存在多少个打斗镜头和接吻镜头，上图中问号位置是该未知电影出现的镜头数图形化展示，具体数字参见下表。

即使不知道未知电影属于哪种类型，我们也可以通过某种方法计算出来。首先计算未知电影与样本集中其他电影的距离，如图所示。

现在我们得到了样本集中所有电影与未知电影的距离，按照距离递增排序，可以找到K个距
离最近的电影。假定k=3，则三个最靠近的电影依次是California Man、He’s Not Really into Dudes、Beautiful Woman。K-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片。

欧几里得距离(Euclidean Distance)

欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

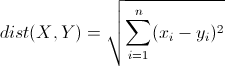
import numpy as np
import pandas as pd

from sklearn.neighbors import KNeighborsClassifier

movie =pd.read_excel('../data/tests.xlsx',sheet_name=1)
movie

	电影名称	武打镜头	接吻镜头	分类情况
0	大话西游	36	1	动作片
1	杀破狼	43	2	动作片
2	前任3	0	10	爱情片
3	战狼2	59	1	动作片
4	泰坦尼克号	1	15	爱情片
5	星语心愿	2	19	爱情片

# X 是数据
X = movie[['武打镜头','接吻镜头']]
X

	武打镜头	接吻镜头
0	36	1
1	43	2
2	0	10
3	59	1
4	1	15
5	2	19

# Y 是目标值
Y =movie['分类情况']
Y

0    动作片
1    动作片
2    爱情片
3    动作片
4    爱情片
5    爱情片
Name: 分类情况, dtype: object

knn=KNeighborsClassifier(n_neighbors=5)

#该方法就是训练数据
knn.fit(X,Y)

# 预测新电影
#碟中谍6 100 ，3
# 战狼2  200 ，1
#山楂树  0   ，10
X_test=pd.DataFrame({'武打镜头':[100,200,0],"接吻镜头":[3,1,10]})
X_test

	武打镜头	接吻镜头
0	100	3
1	200	1
2	0	10

knn.predict(X_test)
#array(['动作片', '动作片', '爱情片'], dtype=object)

# 算法推理

s=((movie['武打镜头'] - 100 )**2  +(movie['接吻镜头'] - 3)**2) **0.5
index=s.sort_values().index
index
#Int64Index([3, 1, 0, 5, 4, 2], dtype='int64')

movie['分类情况'][index[:5]]

3    动作片
1    动作片
0    动作片
5    爱情片
4    爱情片
Name: 分类情况, dtype: object

#  碟中谍6是动作片的概率是60% ,爱情片概率是40%
knn.predict_proba(X_test)
#array([[0.6, 0.4],
       [0.6, 0.4],
       [0.4, 0.6]])

2、在scikit-learn库中使用k-近邻算法

• 分类问题：from sklearn.neighbors import KNeighborsClassifier

• 回归问题：from sklearn.neighbors import KNeighborsRegressor

0）一个最简单的例子

身高、体重、鞋子尺码数据对应性别

X_train = [[180, 180, 43], [170, 150, 39], [173, 128, 43], [170, 140, 39], [163, 90, 39], [164, 85, 36.5], [155, 75, 35], [172, 110, 41], [165, 114, 40], [175, 130, 43], [171, 135, 43], [160, 90, 36],[160, 90, 36], [158, 85, 36]]
y_train = ['男', '男', '男','男', '男', '女', '女', '女', '男', '男', '男', '女', '女', '女']

knn = KNeighborsClassifier()
knn.fit(X_train, y_train)

X_test = [[173, 118, 42], [173, 145, 41], [173, 120, 40], [165, 95, 40], [160, 120, 41], [158, 100, 36]]
knn.predict(X_test)
#array(['男', '男', '男', '女', '男', '女'], dtype='<U1')

knn.score(X_train,  y_train)
#0.8571428571428571

knn.score(X_test, ['男', '男', '女', '女', '男', '女'])
#0.8333333333333334

1）用于分类

导包，机器学习的算法KNN、数据鸢尾花、

from sklearn.datasets import load_iris

iris = load_iris()
iris

获取训练样本

data = iris['data']
target = iris['target']

X_train, X_test, y_train, y_test  = train_test_split(data, target, test_size=0.2)

knn = KNeighborsClassifier()
knn.fit(X_train, y_train).score(X_train, y_train)
knn.score(X_test, y_test)
#0.9666666666666667

knn.score(X_test, y_test)
#1.0

from pandas import DataFrame

# 从4个特征中选出两个特征来画散点图
df = DataFrame(data=data)
df.head()

	0	1	2	3
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

df.plot()

# 选择前两个特征
data = data[:,0:2]
data.shape
#(150, 2)

plt.scatter(data[:,0], data[:,1], c=target)

# 先生成线段上的范围
x, y = np.linspace(data[:,0].min(), data[:,0].max(), 1000), np.linspace(data[:,1].min(), data[:,1].max(), 1000)
# 范围拉起来变成2维平面
X,Y = np.meshgrid(x,y)
# 取两个平面相交的点
XY = np.c_[X.ravel(), Y.ravel()]

display(X, Y)

array([[4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       ...,
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ]])

array([[2.       , 2.       , 2.       , ..., 2.       , 2.       ,
        2.       ],
       [2.0024024, 2.0024024, 2.0024024, ..., 2.0024024, 2.0024024,
        2.0024024],
       [2.0048048, 2.0048048, 2.0048048, ..., 2.0048048, 2.0048048,
        2.0048048],
       ...,
       [4.3951952, 4.3951952, 4.3951952, ..., 4.3951952, 4.3951952,
        4.3951952],
       [4.3975976, 4.3975976, 4.3975976, ..., 4.3975976, 4.3975976,
        4.3975976],
       [4.4      , 4.4      , 4.4      , ..., 4.4      , 4.4      ,
        4.4      ]])

display(XY)

array([[4.3       , 2.        ],
       [4.3036036 , 2.        ],
       [4.30720721, 2.        ],
       ...,
       [7.89279279, 4.4       ],
       [7.8963964 , 4.4       ],
       [7.9       , 4.4       ]])

display(X)
display(X.ravel())

array([[4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       ...,
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ],
       [4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
        7.9       ]])

array([4.3       , 4.3036036 , 4.30720721, ..., 7.89279279, 7.8963964 ,
       7.9       ])

knn = KNeighborsClassifier()
knn.fit(data, target)

# 预测
y_ = knn.predict(XY)

y_[:100]

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])

plt.scatter(XY[:,0], XY[:,1], c=y_)
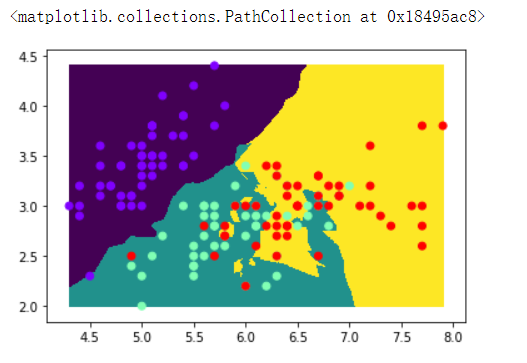
plt.scatter(data[:,0], data[:,1], c=target, cmap='rainbow')

plt.pcolormesh(X, Y , y_.reshape(1000,1000))
plt.scatter(data[:,0], data[:,1], c=target, cmap='rainbow')

绘制图形

定义KNN分类器

第一步，训练数据

第二步预测数据：，所预测的数据，自己创造，就是上面所显示图片的背景点

生成预测数据

对数据进行预测

显示数据

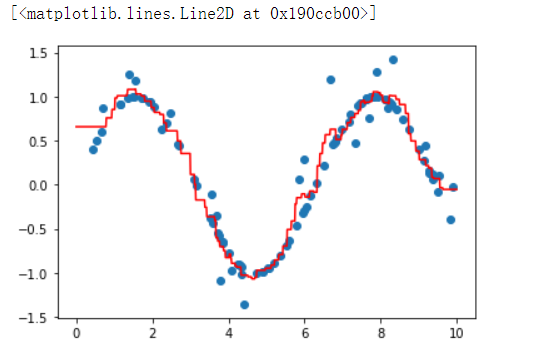
2）用于回归

回归用于对趋势的预测

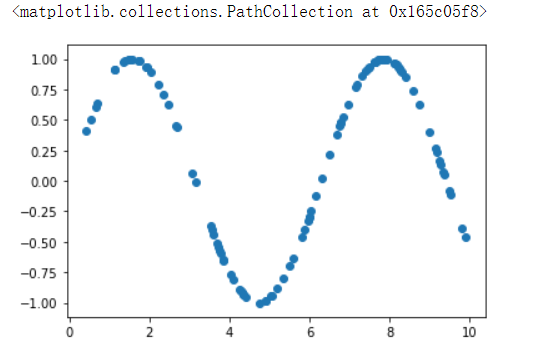
x = np.random.rand(100) * 10 
y = np.sin(x)
plt.scatter(x,y)

# 加点噪声
y[::4] += np.random.randn(25) * 0.3 
plt.scatter(x,y)

from sklearn.neighbors import KNeighborsRegressor

knn = KNeighborsRegressor()
knn.fit(x.reshape(-1,1), y)

X_test = np.linspace(0, 10, 1000).reshape(-1,1)
y_ = knn.predict(X_test)
plt.scatter(x,y)
plt.plot(X_test, y_, c='r')

导包

生成样本数据

生成测试数据的结果

第一步：生成模型，并训练数据

第二步：使用模型，预测数据

绘图显示数据

练习

人类动作识别
步行，上楼，下楼，坐着，站立和躺着

数据采集每个人在腰部穿着智能手机，进行了六个活动（步行，上楼，下楼，坐着，站立和躺着）。采用嵌入式加速度计和陀螺仪，以50Hz的恒定速度捕获3轴线性加速度和3轴角速度，来获取数据

导入数据

X_train = np.load('../data/动作分析/x_train.npy')
X_test = np.load('../data/动作分析/x_test.npy')
y_train = np.load('../data/动作分析/y_train.npy')
y_test = np.load('../data/动作分析/y_test.npy')

X_train.shape
#(7352, 561)

X_test.shape
#(2947, 561)

knn = KNeighborsClassifier()
knn.fit(X_train, y_train)

knn.score(X_train, y_train)
#0.9843579978237215

y_ = knn.predict(X_test)

knn.score(X_test,y_test)
#0.9015948422124194

y_
#array([5, 5, 5, ..., 2, 2, 1], dtype=int64)

label = {1:'WALKING', 2:'WALKING UPSTAIRS', 3:'WALKING DOWNSTAIRS',4:'SITTING', 5:'STANDING', 6:'LAYING'}

# 可视化预测结果
# 6行4列  24个
plt.figure(figsize=(4*4, 5 * 6))
for i in range(24):
    axes = plt.subplot(6,4,i+1)
    axes.plot(X_test[i*100])
    
    if y_test[i*100] != y_[i*100]:
        axes.set_title('True: %s\nPredict:%s'% (label[y_test[i*100]], label[y_[i*100]]), fontdict=dict(fontsize=20, color='r'))
    axes.set_title('True: %s\nPredict:%s'% (label[y_test[i*100]], label[y_[i*100]]))
    

​

​

获取数据

绘制

癌症预测

# 知识点,交叉表
cancer = pd.read_csv('../data/cancer.csv', sep='\t')
cancer.head(20)
# B : benign
# M : malignant

	ID	Diagnosis	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave_mean	...	radius_max	texture_max	perimeter_max	area_max	smoothness_max	compactness_max	concavity_max	concave_max	symmetry_max	fractal_max
0	842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.26540	0.4601	0.11890
1	842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.18600	0.2750	0.08902
2	84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.24300	0.3613	0.08758
3	84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.25750	0.6638	0.17300
4	84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.16250	0.2364	0.07678
5	843786	M	12.45	15.70	82.57	477.1	0.12780	0.17000	0.15780	0.08089	...	15.47	23.75	103.40	741.6	0.1791	0.5249	0.5355	0.17410	0.3985	0.12440
6	844359	M	18.25	19.98	119.60	1040.0	0.09463	0.10900	0.11270	0.07400	...	22.88	27.66	153.20	1606.0	0.1442	0.2576	0.3784	0.19320	0.3063	0.08368
7	84458202	M	13.71	20.83	90.20	577.9	0.11890	0.16450	0.09366	0.05985	...	17.06	28.14	110.60	897.0	0.1654	0.3682	0.2678	0.15560	0.3196	0.11510
8	844981	M	13.00	21.82	87.50	519.8	0.12730	0.19320	0.18590	0.09353	...	15.49	30.73	106.20	739.3	0.1703	0.5401	0.5390	0.20600	0.4378	0.10720
9	84501001	M	12.46	24.04	83.97	475.9	0.11860	0.23960	0.22730	0.08543	...	15.09	40.68	97.65	711.4	0.1853	1.0580	1.1050	0.22100	0.4366	0.20750
10	845636	M	16.02	23.24	102.70	797.8	0.08206	0.06669	0.03299	0.03323	...	19.19	33.88	123.80	1150.0	0.1181	0.1551	0.1459	0.09975	0.2948	0.08452
11	84610002	M	15.78	17.89	103.60	781.0	0.09710	0.12920	0.09954	0.06606	...	20.42	27.28	136.50	1299.0	0.1396	0.5609	0.3965	0.18100	0.3792	0.10480
12	846226	M	19.17	24.80	132.40	1123.0	0.09740	0.24580	0.20650	0.11180	...	20.96	29.94	151.70	1332.0	0.1037	0.3903	0.3639	0.17670	0.3176	0.10230
13	846381	M	15.85	23.95	103.70	782.7	0.08401	0.10020	0.09938	0.05364	...	16.84	27.66	112.00	876.5	0.1131	0.1924	0.2322	0.11190	0.2809	0.06287
14	84667401	M	13.73	22.61	93.60	578.3	0.11310	0.22930	0.21280	0.08025	...	15.03	32.01	108.80	697.7	0.1651	0.7725	0.6943	0.22080	0.3596	0.14310
15	84799002	M	14.54	27.54	96.73	658.8	0.11390	0.15950	0.16390	0.07364	...	17.46	37.13	124.10	943.2	0.1678	0.6577	0.7026	0.17120	0.4218	0.13410
16	848406	M	14.68	20.13	94.74	684.5	0.09867	0.07200	0.07395	0.05259	...	19.07	30.88	123.40	1138.0	0.1464	0.1871	0.2914	0.16090	0.3029	0.08216
17	84862001	M	16.13	20.68	108.10	798.8	0.11700	0.20220	0.17220	0.10280	...	20.96	31.48	136.80	1315.0	0.1789	0.4233	0.4784	0.20730	0.3706	0.11420
18	849014	M	19.81	22.15	130.00	1260.0	0.09831	0.10270	0.14790	0.09498	...	27.32	30.88	186.80	2398.0	0.1512	0.3150	0.5372	0.23880	0.2768	0.07615
19	8510426	B	13.54	14.36	87.46	566.3	0.09779	0.08129	0.06664	0.04781	...	15.11	19.26	99.70	711.2	0.1440	0.1773	0.2390	0.12880	0.2977	0.07259

20 rows × 32 columns

data = cancer.iloc[:,  2:]
target = cancer.Diagnosis

X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=69)

cancer.shape
#(569, 32)

knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
y_ = knn.predict(X_test)
knn.score(X_train, y_train)
#0.94

knn.score(X_test, y_test)
#0.9565217391304348

# 对于这种不太好进行可视化展示的数据,我们可以使用交叉表.
pd.crosstab(index=y_test, columns=y_, rownames=['真实值'], colnames=['预测值'], margins=True)

预测值	B	M	All
真实值
B	44	0	44
M	3	22	25
All	47	22	69

(44 + 22) / 69
#0.9565217391304348

# 混淆矩阵
from sklearn.metrics import confusion_matrix

confusion_matrix(y_test, y_)

# array([[44,  0],
#        [ 3, 22]], dtype=int64)