时间序列分解法

news2024/9/23 3:22:26

影响时间序列变化的因素通常由长期趋势，季节变动，周期变动，不规则变动几部分组成

长期趋势指现象在较长时期内持续发展变化的一种趋向或状态。
季节变动是由于季节的变化引起的现象发展水平的规则变动（波动长度固定）
周期变动指在某段时间内，不具严格规则的周期性连续变动（波动长度不固定）
不规则变动又称随机变动，指由于众多偶然因素对时间序列造成的影响
当时间序列分解成长期趋势( $T_{t}$ )、季节变动( $S_{t}$ )、周期变动( $C_{t}$ )和不规则变动( $I_{t}$ )四个因素后，可认为时间序列Y是这四个因素的函数：
$Y_{t} = f(T_{t},S_{t},C_{t},I_{t})$ 时间序列分解常用的模型有加法模型和乘法模型，加法模型为： $Y_{t} = T_{t}+S_{t}+C_{t}+I_{t}$ 乘法模型为： $Y_{t} = T_{t} \times S_{t} \times C_{t} \times I_{t}$ 其中，乘法模型应用得比较广泛。在乘法模型中，时间序列值Y和长期趋势用绝对数表示，季节变动、周期变动和不规则变动用相对数（百分数）表示。

1、季节指数S的计算

（1）季节指数的计算是先用移动平均法剔除长期趋势和周期变动，再用按季平均法求出季节指数。
示例如下：

用移动平均法测定各季的长期趋势：

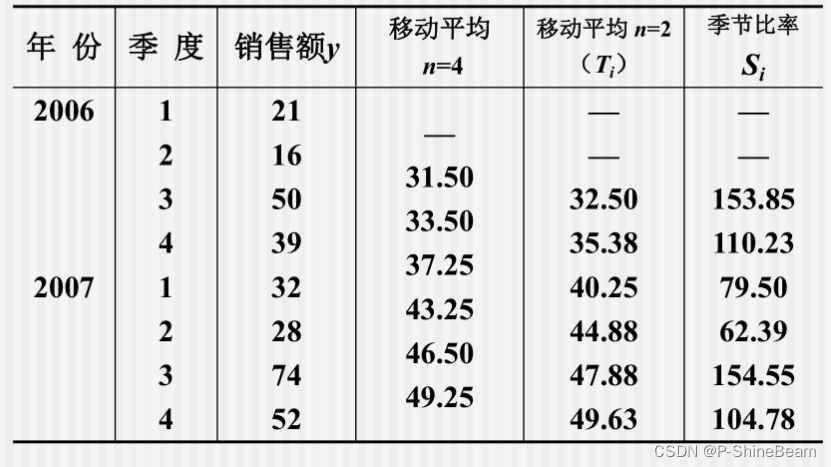
计算各季平均季节比率S:

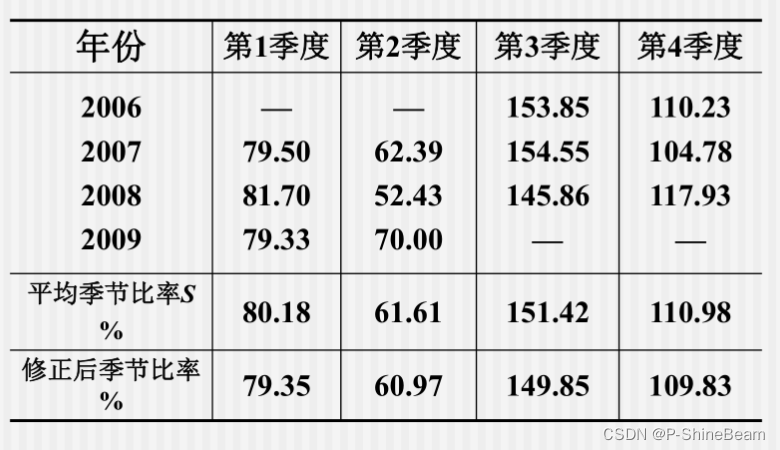
计算修正系数：

（2）气温的波动主要受两个因素的影响；一个是季节效应；一个是随机波动。要求出气温变化时间序列每个月的季节指数 $S_{1}、S_{2}、...S_{12}$ ，第i年第j个月的平均气温可以表示为：
$x_{ij} = \bar{x} \cdot S_{j}+ I_{ij}$ $j = 1, 2..., 12$
式中， $\bar{x}$ 为各月总平均气温； $S_{j}$ 为第j月的季节指数。 $I_{ij}$ 为第i年第j个月的气温的随机波动。
季节指数的计算分为三步：

第一步：计算周期内各期平均数，得到长期一来该时期的平均水平。假定序列的数据结构为m期为一周期，共有n个周期。则：
$\bar{ x_{k}} = \frac{\sum_{n}^{i=1}x_{k} }{n}$ $k = 1, 2, 3, ... m$
第二步：计算总平均数
$\bar{ x} = \frac{\sum_{n}^{i=1}\sum_{m}^{k=1}x_{ik} }{nm}$
第三步：用时期平均数除以总平均数就可以得到各时期的季节指数 $S_{k} (k=1,2,...m)$ ，即：
$S_{k} = \frac{\bar{x_{k}}}{\bar{ x}}$ $k = 1, 2, 3, ... m$

2、长期趋势T的计算

有些时间序列具有非常显著的趋势，有时我们分析的目的就是找到序列中的这种趋势，并利用这种趋势对序列的发展做出合理的预测。
（1）趋势拟合法
趋势拟合法是把时间作为自变量，相应的序列观察值作为因变量，建立序列值随时间变化的回归模型的方法。根据序列表现出的线性或非线性特征分为线性拟合和曲线拟合。
（2）平滑法
平滑法是进行趋势分析和预测时常用的一种方法，利用修匀技术削弱短期随机波动对序列的影响，使序列平滑化，从而显示出变化的规律。根据平滑技术的不同，平滑法可分为移动平均法和指数平滑法。