在射频、微波中，常常使用史密斯圆图来做阻抗匹配。在不涉及复杂的数学推导，仍能把圆图用起来。

比如，共轭匹配。

RL=1+jX，需要找到-jX来抵消+jX，消掉虚部之后，只留下实部，最终等效为RL‘=1。

史密斯圆图是由复数坐标系转化而来的。

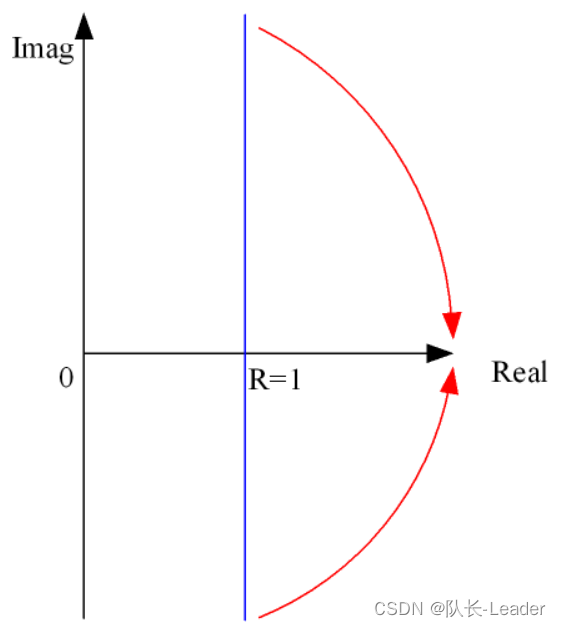
 由于电阻只有大于等于0的数，所以把实轴上的负数部分去掉，再把虚轴的两头向右掰弯，就得到了史密斯圆图。如下图所示。

 

 上图为阻抗的史密斯圆图。

最左边r=0，为短路点，对应复数坐标的原点0。

最右边r=∞，为开路点，对应复数坐标的无穷大。

上半圆为感抗，对应复数坐标虚部大于0（+jX）的上半平面。

下半圆为容抗，对应复数坐标虚部小于0（-jX）的下半平面。

而感抗为jwL，容抗为(-j)/(wC)。

圆图中间的横线，对应复数的实轴，为纯阻性。

一般史密斯圆图都做了归一化，所以在纯阻性1的点，为匹配点，即圆心。

再看下图蓝线，复数域中实部都等于1的的线，也同样两头向右掰弯，就得到等电阻圆（史密斯圆图中的小圆）。

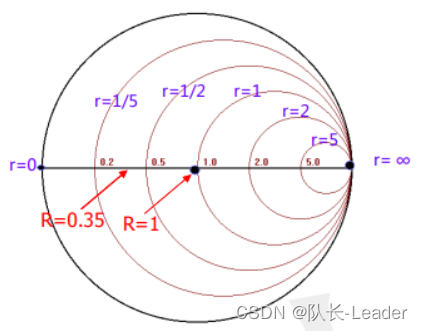
 同样，也能得到等感抗线，与等容抗线。

 

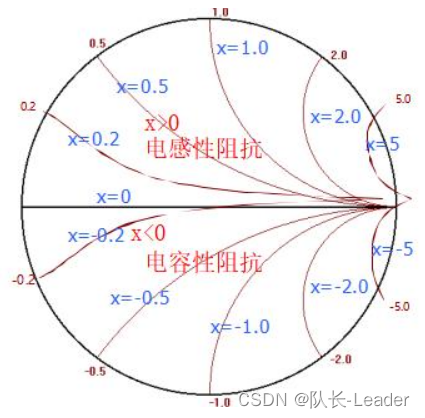
怎样从圆图中走线的方向，得知串并电感，还是串并电容？

在上半圆，朝着感抗增大的方向，就是串电感；朝着感抗减小的方向，就是并电感。

在下半圆，朝着容抗增大的方向，就是并电容；朝着容抗减小的方向，就是串电容。

电感电容的串并公式，这里不再赘述。

需要注意的是，要先知道圆图是阻抗圆，还是导纳圆。

上面都是介绍阻抗圆的，而导纳圆则镜像过来，因为G=1/R。