【深度学习/机器学习】为什么要归一化？归一化方法详解

1. 介绍

1.1 什么是归一化

在机器学习领域中，不同评价指标（即一组特征中的不同特征就是所述的不同评价指标）往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。即，原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。

其中，最典型的就是数据的归一化处理。简而言之，归一化的目的就是使得预处理的数据被限定在一定的范围内（比如[0,1]或者[-1,1]），从而消除奇异样本数据导致的不良影响。

• 在统计学中，归一化的具体作用是归纳统一样本的统计分布性。归一化在[0,1]之间是统计的概率分布，而归一化在[-1,+1]之间是统计的坐标分布。

• 奇异样本数据是指相对于其他输入样本特别大或特别小的样本矢量（即特征向量），譬如，下面为具有两个特征的样本数据x1、x2、x3、x4、x5、x6（特征向量—>列向量），其中x6这个样本的两个特征相对其他样本而言相差比较大，因此，x6认为是奇异样本数据。
  

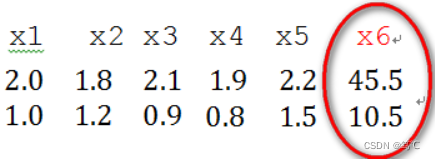
奇异样本数据的存在会引起训练时间增大，同时也可能导致无法收敛，因此，当存在奇异样本数据时，在进行训练之前需要对预处理数据进行归一化；反之，不存在奇异样本数据时，则可以不进行归一化。总结就是，

• 如果不进行归一化，那么由于特征向量中不同特征的取值相差较大，会导致目标函数变“扁”。这样在进行梯度下降的时候，梯度的方向就会偏离最小值的方向，走很多弯路，即训练时间过长。
• 如果进行归一化以后，目标函数会呈现比较“圆”，这样训练速度大大加快，少走很多弯路。

1.2 归一化的好处

归一化有如下好处：

• 归一化后加快了梯度下降求最优解的速度；
• 归一化有可能提高精度（如KNN）

另外没有一种数据标准化的方法，放在每一个问题，放在每一个模型，都能提高算法精度和加速算法的收敛速度。

2. 归一化方法

2.1 最大最小标准化（Min-Max Normalization）

又称为离差标准化，使特征值值映射到 [0 , 1]之间，转换函数如下：

$x^{\prime }=\frac{x-min(x)}{max(x)-min(x)}$

• 适用情况：数值比较集中
• 缺陷：如果max和min不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不稳定。实际使用中可以用经验常量来替代max和min。
• 应用场景：在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法（不包括Z-score方法）。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

2.2 Z-score标准化方法

这种方法基于原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。将A的原始值x使用z-score标准化到x’。转换函数如下：

$x^{\prime }=\frac{x-\mu }{\sigma }$
其中μ为所有样本数据的均值，σ为所有样本数据的标准差。

• 适用情况：该属性特征的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。注意：该方法要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。
• 应用场景：在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，Z-score standardization表现更好。

2.3 非线性归一化

该类归一化方法经常用在数据分化比较大的场景，有些数值很大，有些很小。通过一些数学函数，将原始值进行映射。该类方法包括 tanh（-1，1）、sigmoid（0，1）、softmax（0，1），relu(0, +∞)等，需要根据数据分布的情况，决定非线性函数的曲线。类似于一些激活函数，参考：激活函数说明。

• 适用情况：神经网络中隐藏层之后的操作，可以引入非线性。

2.4 L范数归一化方法（最典型的是L2范数归一化）

L范数归一化方法，对应的转换函数为:

$x^{\prime }=\frac{x}{max(||x|{|}_p,\theta )}$

其中$theta$ 是为了防止除0，一般设置为1e-12。其中$L_p$范数被定义为：

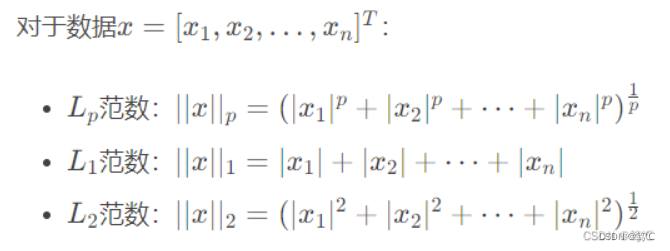
• 适用场景：网络线性层之后，可以避免某些特征过大或者过小。

3. 应用场景说明

• 概率模型不需要归一化，因为这种模型不关心变量的取值，而是关心变量的分布和变量之间的条件概率；

• SVM、线性回归之类的最优化问题需要归一化，是否归一化主要在于是否关心变量取值；

• 神经网络需要标准化处理，一般变量的取值在-1到1之间，这样做是为了弱化某些变量的值较大而对模型产生影响。一般神经网络中的隐藏层采用tanh激活函数比sigmod激活函数要好些，因为tanh双曲正切函数的取值[-1,1]之间，均值为0.

• 在K近邻算法中，如果不对解释变量进行标准化，那么具有小数量级的解释变量的影响就会微乎其微。

4. 参考

【1】https://blog.csdn.net/qq_23100417/article/details/84347475