目录
转换器(transformer)和估计器(estimator)
K-近邻(K-Nearest Neighbors,简称KNN)算法
模型选择与调优
交叉验证(Cross-validation)
GridSearchCV API
朴素贝叶斯(Naive Bayes) 算法
MultinomialNB 和 GaussianNB 区别
决策树(Decision Tree)
随机森林
转换器(transformer)和估计器(estimator)
在Scikit-learn中,转换器(transformer)和估计器(estimator)是机器学习管道(pipeline)的两个重要组成部分。
转换器是将一个数据集转换成另一个数据集的算法。例如,使用Scikit-learn的预处理模块中的StandardScaler对数据集进行标准化,或使用CountVectorizer将文本数据集转换为特征矩阵。转换器通常通过fit()方法学习数据集的某些属性,然后通过transform()方法将其转换成另一个数据集。
估计器是一种机器学习算法,它通过对已知的数据集进行学习来对新数据进行预测。例如,使用Scikit-learn的线性回归模型进行预测,或使用KMeans模型对数据进行聚类。估计器通常使用fit()方法在已知的数据集上进行训练,然后使用predict()方法对新数据进行预测。
除了fit()和transform()方法外,许多转换器和估计器还具有fit_transform()方法,该方法将学习和转换组合成单个操作,从而提高了代码的效率。
Scikit-learn提供了许多常用的转换器和估计器,它们具有统一的API接口,可以非常方便地在机器学习管道中组合使用。使用转换器和估计器,可以将数据集进行处理和预测,从而得到更好的模型性能。
K-近邻(K-Nearest Neighbors,简称KNN)算法
K-近邻(K-Nearest Neighbors,简称KNN)是一种基本的分类和回归算法。KNN的基本思想是在数据集中寻找K个距离新实例最近的训练样本,然后根据这K个样本的类别来对新实例进行分类或回归预测。KNN是一种无参数的学习算法,它没有显式地学习一个模型,而是直接根据已有的数据进行预测。
KNN算法的步骤如下:
- 计算测试数据与训练集中每个样本的距离,常用的距离度量有欧氏距离、曼哈顿距离、余弦相似度等。
- 选取与测试数据距离最近的K个训练集样本。
- 统计这K个样本中出现次数最多的类别作为测试数据的类别,即进行分类预测,或计算这K个样本的平均值作为测试数据的预测值,即进行回归预测。
KNN算法的优点在于简单易懂、无需显式地学习模型、适用于分类和回归问题,但是在处理大规模数据集时速度较慢,需要保存全部训练数据,对于高维数据效果不佳。
下面是一个使用Scikit-learn实现KNN分类算法的Python代码案例
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier # 加载iris数据集 iris = load_iris() # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=42) # 创建KNN分类器模型 knn = KNeighborsClassifier(n_neighbors=3) # 训练模型 knn.fit(X_train, y_train) # 预测测试集 y_pred = knn.predict(X_test) #查看预估与测试值 print("查看预估数值:\n",y_pred==y_test) # 输出模型准确率 accuracy = knn.score(X_test, y_test) print("KNN模型的准确率为:", accuracy)
以上代码中,首先使用
load_iris()函数加载iris数据集,然后使用train_test_split()函数将数据集划分为训练集和测试集。接着使用KNeighborsClassifier创建KNN分类器模型,并使用fit()方法训练模型。最后使用predict()方法对测试集进行预测,并使用score()方法计算模型准确率。
模型选择与调优
模型选择是指在给定数据集和模型族的情况下,从中选择最优模型的过程。而模型调优则是在选择好模型后,对模型参数进行优化以达到更好的模型效果。
交叉验证(Cross-validation)
交叉验证(Cross-validation)是一种常用的模型选择和调优的方法。交叉验证将原始数据集分成K个子集,然后使用其中K-1个子集作为训练集,剩余的一个子集作为测试集。这个过程会重复K次,每次用不同的子集作为测试集。最终,将这K次的测试结果平均得到模型的性能指标。
交叉验证可以有效地评估模型的性能,同时还能防止过拟合。它也可以帮助我们选择模型的超参数,即模型构建时需要手动调整的参数,比如KNN模型的k值、线性模型的正则化参数等等。为了选出最优的超参数组合,我们可以使用超参数搜索算法。
网格搜索(Grid Search)是一种常用的超参数搜索算法。它会在给定的超参数空间中进行穷举搜索,并使用交叉验证来评估每种超参数组合的性能。网格搜索通常需要指定一个参数字典,其中每个键表示一个超参数,对应的值是一个超参数的取值列表。然后网格搜索会遍历所有超参数组合,返回性能最优的超参数组合。
GridSearchCV API
GridSearchCV 是一个用于超参数优化的工具,可以通过系统地遍历不同的参数组合来找到最佳的模型参数,进而提高模型的性能。下面是几个常用的参数及其意义:
estimator: 传入一个模型对象,该模型需要实现fit()和predict()方法,这个模型会在参数网格上进行优化。param_grid: 一个字典或列表,用于指定参数的取值范围,网格搜索会遍历所有的参数组合,将最优参数组合作为模型的最终参数。cv: 交叉验证生成器或迭代器,用于确定交叉验证的折数或生成样本的分割策略。scoring: 模型评价标准,可以是字符串、自定义函数或可调用的对象,用于对每个候选参数组合进行评价。n_jobs: 并行运行的作业数。verbose: 控制详细程度的参数,可以设置为 0(不输出任何信息)到 10(输出所有信息)之间的值。
下面是一个简单的示例,演示如何使用交叉验证和网格搜索来选择最优的KNN模型超参数对上一个python示例代码进行优化
from sklearn.datasets import load_iris from sklearn.model_selection import GridSearchCV, train_test_split from sklearn.neighbors import KNeighborsClassifier # 加载数据 iris = load_iris() X, y = iris.data, iris.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42) # 定义KNN模型 knn = KNeighborsClassifier() # 定义参数的搜索空间 param_grid = {'n_neighbors': [1, 3, 5, 7, 9]} # 使用GridSearchCV进行模型选择和调优 grid_search = GridSearchCV(knn, param_grid=param_grid, cv=5) grid_search.fit(X_train, y_train) # 输出最优参数和交叉验证的结果 print('Best parameter:', grid_search.best_params_) print('Best cross-validation score:', grid_search.best_score_) print('Test set score:', grid_search.score(X_test, y_test))
上述代码中,首先加载数据,然后划分训练集和测试集。接着,定义KNN模型,并定义参数的搜索空间。然后使用GridSearchCV进行模型选择和调优。最后输出最优参数和交叉验证的结果。
朴素贝叶斯(Naive Bayes) 算法
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的分类算法,它假设样本特征之间相互独立,因此被称为“朴素”。
朴素贝叶斯算法在文本分类、垃圾邮件过滤、情感分析等领域得到广泛应用,其原理是基于贝叶斯定理,通过计算样本在给定类别的条件下的概率来进行分类。
具体来说,对于一个待分类的样本,朴素贝叶斯算法会计算它属于每个类别的概率,并将概率最大的类别作为分类结果。计算样本属于某个类别的概率时,需要通过先验概率和似然概率来计算后验概率。先验概率指的是样本属于某个类别的概率,而似然概率指的是样本在给定类别下的特征出现概率。朴素贝叶斯算法假设样本特征之间相互独立,因此可以将特征的似然概率相乘来计算样本在给定类别下的概率。
MultinomialNB 和 GaussianNB 区别
MultinomialNB适用于特征是离散值的情况,例如文本分类问题,其中特征是单词或短语的出现次数或出现概率。在MultinomialNB中,每个特征的概率分布是一个多项分布。
GaussianNB适用于特征是连续值的情况,例如数据集中的各种测量结果。在GaussianNB中,每个特征的概率分布是一个高斯分布。
在使用朴素贝叶斯分类器时,应根据特征类型选择合适的模型。
下面是一个使用Scikit-learn库中的MultinomialNB和GaussianNB进行文本分类的示例:
from sklearn.naive_bayes import MultinomialNB, GaussianNB from sklearn.feature_extraction.text import CountVectorizer from sklearn.datasets import fetch_20newsgroups from sklearn.model_selection import train_test_split # 加载数据集 newsgroups = fetch_20newsgroups(subset='test',data_home='./data') # 对文本进行特征提取 vectorizer = CountVectorizer() X = vectorizer.fit_transform(newsgroups.data) y = newsgroups.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 使用MultinomialNB进行分类 mnb = MultinomialNB() mnb.fit(X_train, y_train) print("MultinomialNB accuracy:", mnb.score(X_test, y_test)) # 使用GaussianNB进行分类 gnb = GaussianNB() gnb.fit(X_train.toarray(), y_train) print("GaussianNB accuracy:", gnb.score(X_test.toarray(), y_test))
这个例子加载了Scikit-learn库中的20个新闻组数据集,使用CountVectorizer进行文本特征提取,并使用MultinomialNB和GaussianNB进行分类。其中,MultinomialNB适用于文本分类问题,而GaussianNB不太适用。
决策树(Decision Tree)
决策树(Decision Tree)是一种基于树结构的分类器,通过对一系列问题的回答,逐步向下递归,最终得到一棵决策树,每个叶节点代表一种类别。决策树算法的优点是可以处理离散型和连续型数据,且易于理解和解释,缺点是容易产生过拟合。
决策树是一种常用的分类和回归算法,在许多场景下都可以得到很好的应用。一般来说,决策树适用于以下情况:
-
数据量不大且特征比较简单:决策树在处理数据量不大且特征比较简单的数据集时,运行速度较快,同时也比较容易理解和解释生成的决策树。
-
需要理解和解释分类规则:生成的决策树可以用于直观地表示分类规则,可以帮助人们更好地理解和解释分类规则,特别是在一些需要向其他人进行解释的场景中,决策树的解释性非常有用。
-
特征具有一定的可解释性:决策树适用于特征具有一定的可解释性的情况,例如医学诊断等领域中的数据分析,特征的可解释性对于专家评估非常重要。
-
需要进行特征选择:在决策树的构建过程中,根据特征的重要性对特征进行选择,可以得到更简洁、更容易理解和解释的分类器。
class sklearn.tree.DecisionTreeClassifier API是决策树分类器的实现,主要用于分类问题。其中的参数和方法包括:
criterion: 切分质量的评价准则,可选值为"gini"或"entropy"。
splitter: 决策树分裂策略,可选值为"best"或"random"。
max_depth: 决策树最大深度,用于防止过拟合。
min_samples_split: 节点分裂所需的最小样本数。
min_samples_leaf: 叶节点所需的最小样本数。
max_features: 每个节点评估分裂时要考虑的最大特征数。
random_state: 随机数种子,用于控制每次运行时的随机性。
fit(X, y): 拟合决策树模型。
predict(X): 对X进行预测。
score(X, y): 返回模型在测试集上的精度得分。
下面是一个简单的示例,使用 sklearn.tree.DecisionTreeClassifier 对鸢尾花数据集进行分类:
from sklearn.datasets import load_iris from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # 加载数据 iris = load_iris() X, y = iris.data, iris.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建决策树模型 clf = DecisionTreeClassifier(random_state=42) # 训练模型 clf.fit(X_train, y_train) # 在测试集上评估模型 y_pred = clf.predict(X_test) accuracy = accuracy_score(y_test, y_pred) print("Accuracy:", accuracy)
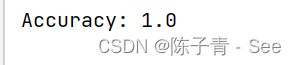
在上面的代码中,首先使用
load_iris()函数加载鸢尾花数据集,然后使用train_test_split()函数将数据集划分为训练集和测试集。接下来,使用DecisionTreeClassifier类创建决策树模型,并使用训练集对模型进行训练。最后,在测试集上评估模型的准确率。
随机森林
在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
学习算法根据下列算法而建造每棵树:
- 用N来表示训练用例(样本)的个数,M表示特征数目。
- 1、一次随机选出一个样本,重复N次, (有可能出现重复的样本)
- 2、随机去选出m个特征, m <<M,建立决策树
- 采取bootstrap抽样(一种随机放回抽样的方法)
RandomForestClassifier的使用方法与其他scikit-learn的分类器类似,可以通过fit()方法拟合模型,predict()方法预测结果,score()方法评估模型性能,等等。其中,最常用的参数包括:
n_estimators:森林中决策树的数量。criterion:决策树的分裂标准,可以选择"gini"或"entropy"。max_depth:决策树的最大深度,控制决策树的复杂度。min_samples_split:决策树分裂所需的最小样本数。min_samples_leaf:叶节点所需的最小样本数。max_features:用于每个决策树的特征数量,可以选择"auto"、"sqrt"、"log2"或任意整数。bootstrap:是否使用有放回的随机抽样来训练每个决策树。
下面是一个使用RandomForestClassifier进行分类的示例代码:
from sklearn.ensemble import RandomForestClassifier from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeClassifier # 生成随机数据 X, y = make_classification(n_samples=10000, n_features=100, n_informative=20, n_classes=5, random_state=1) # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 创建随机森林分类器 clf = RandomForestClassifier(n_estimators=100, max_depth=100) tree =DecisionTreeClassifier() # 训练模型 clf.fit(X_train, y_train) tree.fit(X_train,y_train) # 预测测试集 y_pred = clf.predict(X_test) y_t_pred = tree.predict(X_test) # 评估模型性能 score = clf.score(X_test, y_test) tree_score = tree.score(X_test, y_test) print("Accuracy: {:.2f}%".format(score*100)) print("Tree Accuracy: {:.2f}%".format(tree_score*100))