滑动相关

滑动相关属于一种时域捕获方法，其具体原理是是通过本地序列与接收信号在固定窗长内滑动累加得到相关结果。
一般滑动相关算法可以用于对自相关性非常好的伪码进行同步判决。
我们首先生成一组自相关性很好的初始序列$x(n)$
$$x(n)=e^{\frac{j\pi n^2}{N}},n=1\sim N$$
假设该信号经过信噪比为0dB的信道，得到接收信号$$y(n)=x(n)+w(n)$$
二者做互相关，得到结果
R x y ( m ) = E { x n + m y n ∗ } = E { x n y n − m ∗ } R_{xy}(m) = E\{ x_{n+m}y_{n}^* \}=E\{ x_{n}y_{n-m}^* \} Rxy​(m)=E{xn+m​yn∗​}=E{xn​yn−m∗​}
在此附上互相关的自实现代码(与matlab自带的xcorr实现功能相同)：

function [c,lags] = section_xcorr(x,y)
M = length(x);
N = length(y);
y = [zeros(M-1,1);y;zeros(M-1,1)];

c = zeros(M+N-1,1);
for i = 1:M+N-1
    axis_x = conj(x);
    axis_y = y(i:i+M-1);     
    c(i) = mean(axis_x.*axis_y);
end
    lags = 1:length(c);
    lags = lags - N;
    c = flip(c);
end

相关结果如下：

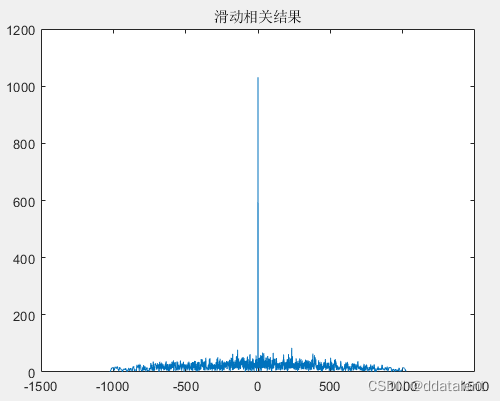
根据该相关峰进行判决，即可完成同步，找到接收序列中信号的帧头位置。

匹配滤波器捕获（DMF）

滑动相关求和累加过程与FIR滤波器相似，，因此诞生了匹配滤波器捕获(DMF)。把本地伪码当做匹配滤波器系数，数据输入滤波器，得到的滤波结果和互相关的结果大致相同。

（在硬件实现层面，例如fpga的实现。调用FIR滤波的IP core远比实现滑动相关求和累加简单得多，因此在同步算法的硬件实现层面，通常采用DMF的算法。不过如果序列过长，可以先下采样，然后对部分序列进行捕获）

滑动相关和卷积的不同在于，卷积需要对其中一个输入进行翻转，因此我们需要把本地序列做共轭翻转后再当作滤波器系数。利用fdatool工具设计滤波器

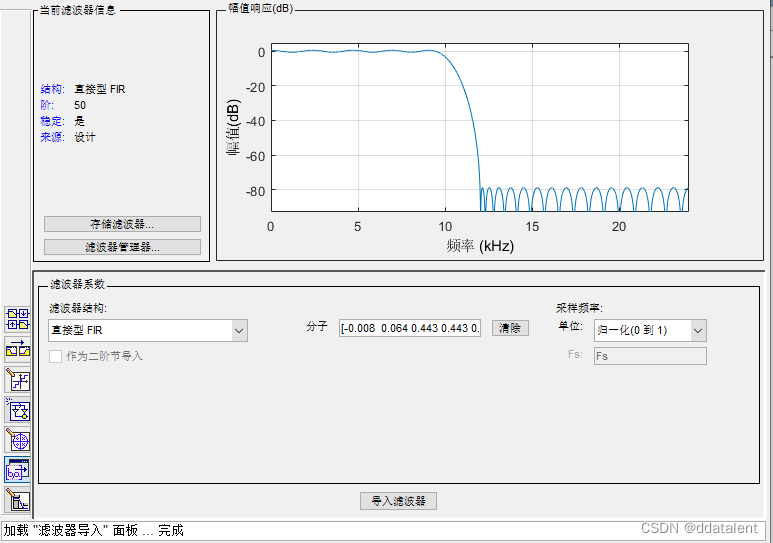
利用该滤波器，对接收数据进行滤波处理，得到滤波后的结果。

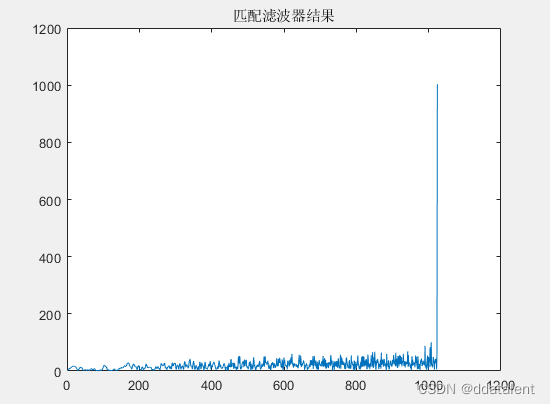
比较互相关的结果和匹配滤波的结果

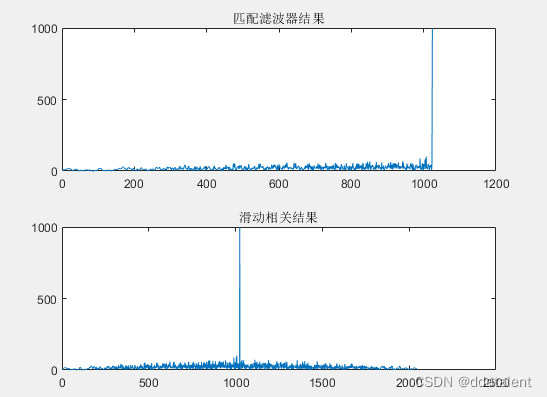
发现二者都出现了幅度相同的峰值结果，但是出现的位置和输出结果都完全不同。这是什么原因呢？

我们将接收数据复制一份，即重复接收两次发射序列，将长度为2N的接收数据同时经过匹配滤波器和互相关。得到如下结果

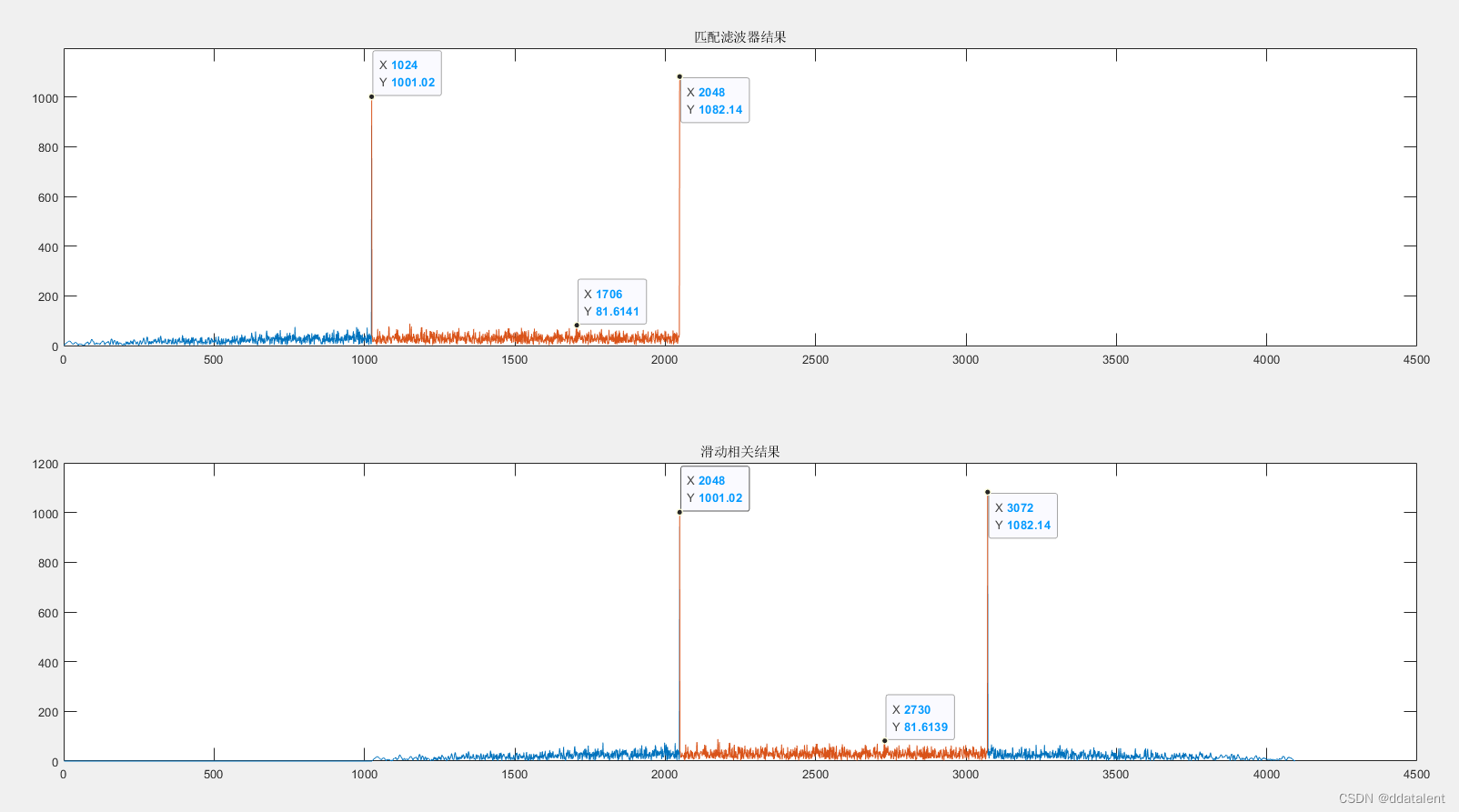
可以看出，在两个相关峰中间的输出，滑动相关和匹配滤波的输出结果是一样的。其他地方的结果不一样主要是因为滑动相关会在数据不足的地方自动补0，而filter函数自带截尾设置，导致数据不足的地方二者输出结果不同。

总体来说，匹配滤波和滑动相关可以实现的功能是相同的。匹配滤波的优点在于捕获时间提升N倍，而缺点在于存在多普勒时捕获带宽较小，相关峰随频率衰减，漏检错检概率较大。

最后附上本仿真的主要代码：

clc;
clear;
close all;
%% 原始信号
length_seq = 1024;
seq = gen_chu_seq(length_seq); %原始数据
seq_noise = awgn([seq seq],0);
%% 设置滤波器系数
h_num = flip(conj(seq)); %用该数据设置滤波器系数
h = matched_filter;      %生成滤波器
%% 匹配滤波器效果
filter_outpiut = filter(h,[seq_noise ]);

figure();
subplot(2,1,1)
plot(abs(filter_outpiut));
hold on
plot(1024:2048,abs(filter_outpiut(1024:2048)));
axis([0,4500,0,1200])
title('匹配滤波器结果')


%% 滑动相关结果
[xcorr_output,lags] = xcorr([seq_noise ],seq);
subplot(2,1,2)
plot(abs(xcorr_output));
hold on
plot(2048:3072,abs(xcorr_output(2048:3072)));
axis([0,4500,0,1200])
title('滑动相关结果')