🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
第四章 向量组的线性相关性
&5)向量空间
第五章 相似矩阵及二次型
&1)向量的内积、长度及正交性
第四章 向量组的线性相关性
&5)向量空间
定义6:设V为n维向量的集合,如果集合V非空,且集合V对于向量的加法及数乘运算封闭,那么就称集合V为向量空间
性质:n元齐次线性方程组的解集
S=|x|Ax=0|
是一个向量空间(称为齐次线性方程组的解空间)因为由齐次线性方程组的解的性质1和性质2,即知其解集S对向量的线性运算封闭
同理的S=|x|Ax=b|不是向量空间(集合S对于向量的加法及数乘运算不封闭)
定义8:设V为向量空间,如果r个向量a[1],a[2],…,a[r]∈V,且满足
(i)a[1],a[2],…,a[r]线性无关;(极大无关组)
(ii)V中任一向量都可由a[1],a[2],…,a[r]线性表示
那么,向量组a[1],a[2],…,a[r]就称为向量空间V的一个基(极大无关组),r称为向量空间V的维数,并称V为r维向量空间
定义9:如果在向量空间V中取一个基a[1],a[2],…,a[r],那么V中任一向量x可惟一地表示为
x=𝛌[1]a[1]+𝛌[2]a[2]+…+𝛌[r]a[r]
数组𝛌[1],𝛌[2],…,𝛌[r]称为向量x在基a[1],a[2],…,a[r]的坐标
过渡矩阵:
P=A^-1·B B=PA(这里的P是矩阵A到B的过渡矩阵)
这里可以用初等变换
第五章 相似矩阵及二次型
&1)向量的内积、长度及正交性
定义1:设有n维向量
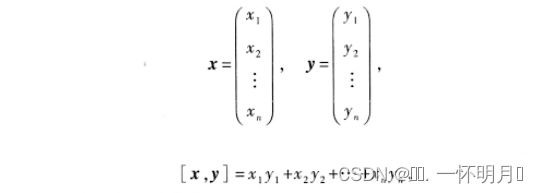
[x,y]称为向量x与y的内积(其实就是向量的点乘)
内积是两个向量之间的一种运算,其结果是一个实数,用矩阵记号表示,当x与y都是列向量时,有
[x,y]=(x^T)·y
内积具有下列性质(其中x,y,z为n维向量,𝛌为实数):
(i)[x,y]=[y,x];
(ii)[𝛌x,y]=𝛌[x,y];
(iii)[x+y,z]=[x,z]+[y,z]
(iv)当x=0时,[x,x]=0;当x!=0时,[x,x]>0
施瓦茨不等式:
[x,x]^2<=[x,x]+[y,y]
定义2:令
||x||=([x,x])^(1/2)=(x[1]^2+x[2]^2+..+x[n]^2)
||x||称为n维向量x的长度(或范数)
向量长度具有下述性质:
(i)非负性 当x!=0,||x||>0;当x=0时,||x||=0;
(ii)齐次性 ||𝛌x||=|𝛌|·||x||;
当||x||=1时,称x为单位向量,若a!=0,取x=a/||a||,则x是一个单位向量,由向量a得到x的过程称为把向量a单位化
正交向量组:是指一组两两正交的非零向量
注:零和任何向量都正交
定理1 若n维向量a[1],a[2],…,a[r]是一组两两正交的非零向量,则a[1],a[2],…,a[r]线性无关
定义3:设n维向量e[1],e[2],…,e[r]是向量空间的V(V⊆R^n(n是维数))的一个基,如果e[1],e[2],…,e[r]两两正交,且都是单位向量,则称e[1],e[2],…,e[r]是V的一个标准正交基,例如
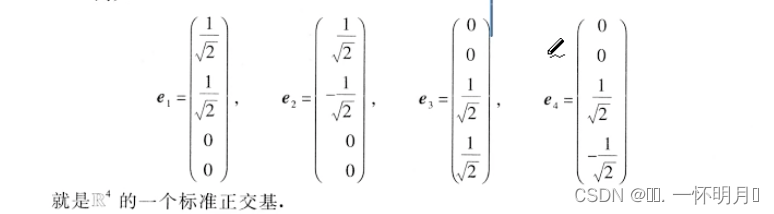
施密特正交化

定义4:如果n阶矩阵A满足
A^T·A=E(即A^-1=A^T)
那么称A为正交矩阵,简称正交阵
正交矩阵的性质:
(I)若A为正交阵,则A^-1=A^T也是正交阵,且|A|=1或(-1);
(ii)若A和B都是正交阵,则AB也是正交阵
定义5:若P为正交矩阵,则线性变换y=Px称为正交变换,则有
||y||=(y^T·y)^(1/2)=(x^T·P^T·P·x)^(1/2)=(x^T·x)^(1/2)=||x||
正交变换的长度保持不变
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸






![[翻译]GPDB中的文件空间与表空间](https://img-blog.csdnimg.cn/img_convert/a91488ee421d46571d604e1e023b61d9.png)



