1、SB树简介
本质上是一棵二叉搜索树,SB树全称 Size Balanced Tree,顾名思义,这是一棵通过大小(Size)域来维持平衡的二叉搜索树。
它不仅支持简单的二叉搜索树操作,也支持 Select 和 Rank。
定义一下Size的概念,对于树上某个节点而言,它的Size指的是以它为树根的子树当中节点的数量。
SB树的平衡条件:对于SBT的每个节点,每棵子树的大小不小于其兄弟的子树大小。
图示: s [ X ] s[X] s[X] 表示以 X X X 为根的子树当中节点的数量。
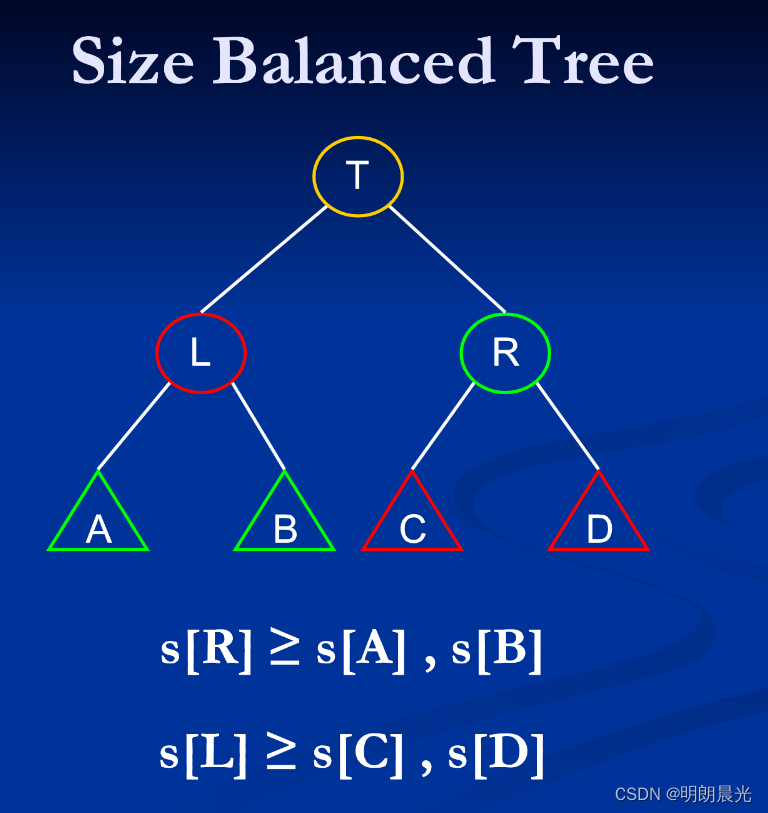
在之前讲解的AVL树中平衡因子是高度,所以每个节点需要维护高度,那么在SB树中平衡因子是节点个数,所以每个节点需要维护节点个数size。
SB树的平衡条件没有AVL树那么严苛,但是也相当平衡。因为SB树的平衡条件限制,所以对于任意节点来说,它左右两棵子树的规模差距都不会到2倍以上,所以可以认为整棵树的高度几乎也就是 l o g N logN logN 的水准,这个 N N N 是树中的节点的数量最大值。
SB树的平衡性相对于AVL树的平衡性来说,进行了一定程度的阉割。
2、SB树的失衡类型
和AVL树一样,SB树的失衡类型也有四种,但是这四种的意义有所不同。
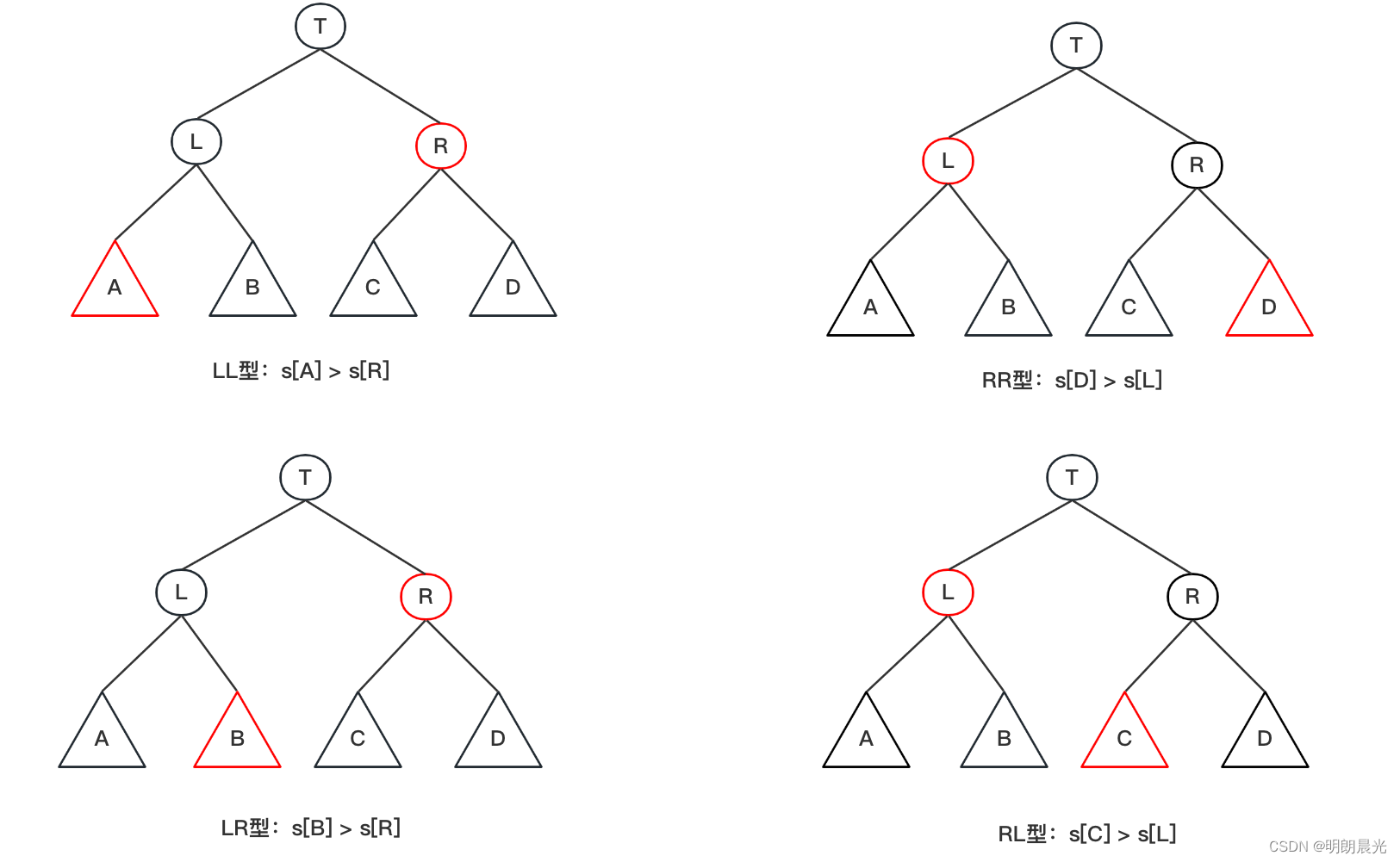
设计一个函数 SBTNode maintain(SBTNode node),作用是调整失衡的SB树,注意传入的是失衡节点的父节点。
LL型失衡的调整:
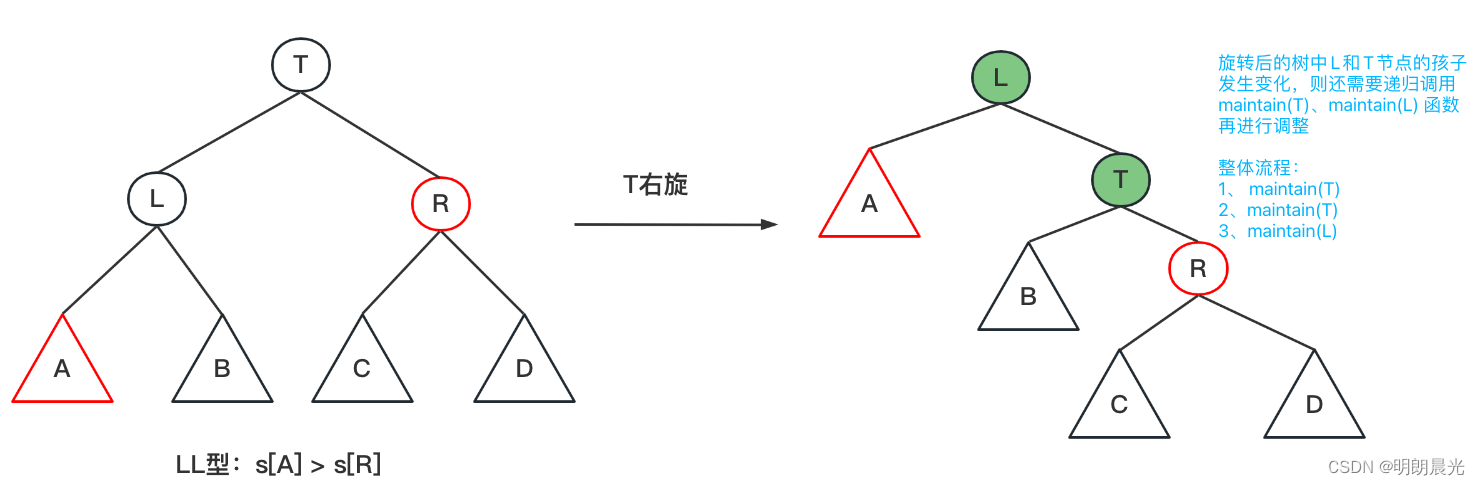
LR型失衡的调整:
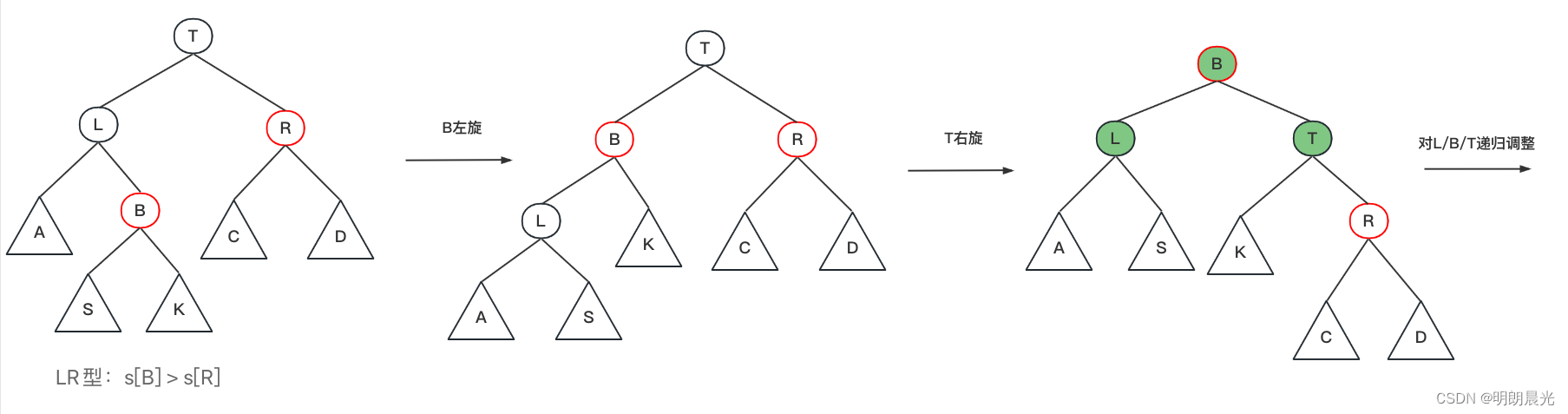
注意和AVL树失衡调整的区别:AVL树发生了LL型失衡则只需要对失衡节点进行一次右旋即可,而SB树发生了LL型失衡需要将失衡节点的父节点进行右旋,然后对右旋后的树中孩子发生变化的节点再进行递归调整。
SB树的RR型失衡和LL型失衡是对称的,所以SB树的RR型失衡也是将失衡节点的父节点进行左旋,然后对左旋后的树中孩子发生变化的节点再进行递归调整。
SB树的LL型、LR型、RR型、RL型失衡的调整动作和AVL树是一样的,不同点在于在调整完后还要审视哪些节点的孩子发生了变化,对于孩子发生变化的节点要做后续的递归调整。
之所以在旋转后要进行递归调整,是因为在旋转后,孩子发生变化的节点的叔叔和侄子关系发生了变化,对于新的叔侄关系需要重新检查是否满足SB树的平衡条件。
和AVL树一样,在新增节点的时候,从新增的节点开始到头结点沿途受影响的节点全部都要调用 maintain 函数进行调整。
SB树在删除节点的时候不进行平衡调整,而是在新增节点的时候才进行平衡调整。但是整个平衡调整是递归行为,平衡调整会传递,所以即使在删除节点的时候不进行平衡调整,只在新增节点的时候调整,依然能把这棵树调整得平衡。这也是为什么建议用Size Balanced Tree去实现有序表,因为它省掉了删除节点时的调整动作。
比较极端的,SB树最大有 N N N 个节点,它的高度最高也就是 l o g N logN logN,如果一直只进行删除操作,那么树有可能变成链状而不平衡,但是没关系,这棵树依然是 l o g N logN logN 性能,因为这个 N N N 就是整棵树能冲到最大节点数量的值,后续如果再加入新的节点,又会进行平衡调整,树又会变得平衡。而AVL树没有递归行为。
3、SB树代码实现
public class SizeBalancedTreeMap {
//SB树节点定义
public static class SBTNode<K extends Comparable<K>, V> {
public K key;
public V value;
public SBTNode<K, V> l;
public SBTNode<K, V> r;
public int size; // 不同的key的数量,节点数量
public SBTNode(K key, V value) {
this.key = key;
this.value = value;
size = 1;
}
}
public static class SizeBalancedTreeMap<K extends Comparable<K>, V> {
private SBTNode<K, V> root;
private SBTNode<K, V> rightRotate(SBTNode<K, V> cur) {
SBTNode<K, V> leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return leftNode;
}
private SBTNode<K, V> leftRotate(SBTNode<K, V> cur) {
SBTNode<K, V> rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return rightNode;
}
//调整平衡:cur这棵树平衡的调整(基于节点数量size)
private SBTNode<K, V> maintain(SBTNode<K, V> cur) {
if (cur == null) {
return null;
}
int leftSize = cur.l != null ? cur.l.size : 0;
int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
int rightSize = cur.r != null ? cur.r.size : 0;
int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
if (leftLeftSize > rightSize) { //LL型失衡
cur = rightRotate(cur); //先进行右旋
cur.r = maintain(cur.r); //递归调用maintain,对右旋后的右孩子进行调整
cur = maintain(cur); //递归调用maintain,对右旋后的根进行调整
} else if (leftRightSize > rightSize) { //LR型失衡,有3个节点的孩子发生了变化,都要递归调用maintain函数进行调整
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
// <=key,离key最近的节点
private SBTNode<K, V> findLastIndex(K key) {
SBTNode<K, V> pre = root;
SBTNode<K, V> cur = root;
while (cur != null) {
pre = cur;
if (key.compareTo(cur.key) == 0) {
break;
} else if (key.compareTo(cur.key) < 0) {
cur = cur.l;
} else {
cur = cur.r;
}
}
return pre;
}
//>=key,离key最近的节点
private SBTNode<K, V> findLastNoSmallIndex(K key) {
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) {
ans = cur;
cur = cur.l;
} else {
cur = cur.r;
}
}
return ans;
}
private SBTNode<K, V> findLastNoBigIndex(K key) {
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) {
cur = cur.l;
} else {
ans = cur;
cur = cur.r;
}
}
return ans;
}
// 现在,以cur为头的树上,新增,加(key, value)这样的记录
// 加完之后,会对cur做检查,该调整调整
// 返回,调整完之后,整棵树的新头部
private SBTNode<K, V> add(SBTNode<K, V> cur, K key, V value) {
if (cur == null) {
return new SBTNode<K, V>(key, value);
} else {
cur.size++;
if (key.compareTo(cur.key) < 0) {
cur.l = add(cur.l, key, value);
} else {
cur.r = add(cur.r, key, value);
}
return maintain(cur);
}
}
// 在cur这棵树上,删掉key所代表的节点
// 返回cur这棵树的新头部
private SBTNode<K, V> delete(SBTNode<K, V> cur, K key) {
cur.size--;
if (key.compareTo(cur.key) > 0) {
cur.r = delete(cur.r, key);
} else if (key.compareTo(cur.key) < 0) {
cur.l = delete(cur.l, key);
} else { // 当前要删掉cur
if (cur.l == null && cur.r == null) {
// free cur memory -> C++
cur = null;
} else if (cur.l == null && cur.r != null) {
// free cur memory -> C++
cur = cur.r;
} else if (cur.l != null && cur.r == null) {
// free cur memory -> C++
cur = cur.l;
} else { // 有左有右
SBTNode<K, V> pre = null;
SBTNode<K, V> des = cur.r;
des.size--;
while (des.l != null) {
pre = des;
des = des.l;
des.size--;
}
if (pre != null) {
pre.l = des.r;
des.r = cur.r;
}
des.l = cur.l;
des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;
// free cur memory -> C++
cur = des;
}
}
//下面这行代码加与不加都可以,通常是在删除的时候不进行调整,反正add的时候会进行调整
// cur = maintain(cur);
return cur;
}
private SBTNode<K, V> getIndex(SBTNode<K, V> cur, int kth) {
if (kth == (cur.l != null ? cur.l.size : 0) + 1) {
return cur;
} else if (kth <= (cur.l != null ? cur.l.size : 0)) {
return getIndex(cur.l, kth);
} else {
return getIndex(cur.r, kth - (cur.l != null ? cur.l.size : 0) - 1);
}
}
public int size() {
return root == null ? 0 : root.size;
}
public boolean containsKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
return lastNode != null && key.compareTo(lastNode.key) == 0 ? true : false;
}
// (key,value) put -> 有序表 新增、改value
public void put(K key, V value) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) {
lastNode.value = value;
} else {
root = add(root, key, value);
}
}
public void remove(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
if (containsKey(key)) {
root = delete(root, key);
}
}
public K getIndexKey(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).key;
}
public V getIndexValue(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).value;
}
public V get(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) {
return lastNode.value;
} else {
return null;
}
}
public K firstKey() {
if (root == null) {
return null;
}
SBTNode<K, V> cur = root;
while (cur.l != null) {
cur = cur.l;
}
return cur.key;
}
public K lastKey() {
if (root == null) {
return null;
}
SBTNode<K, V> cur = root;
while (cur.r != null) {
cur = cur.r;
}
return cur.key;
}
public K floorKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
return lastNoBigNode == null ? null : lastNoBigNode.key;
}
public K ceilingKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
return lastNoSmallNode == null ? null : lastNoSmallNode.key;
}
}
// for test
public static void printAll(SBTNode<String, Integer> head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
// for test
public static void printInOrder(SBTNode<String, Integer> head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.r, height + 1, "v", len);
String val = to + "(" + head.key + "," + head.value + ")" + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.l, height + 1, "^", len);
}
// for test
public static String getSpace(int num) {
String space = " ";
StringBuffer buf = new StringBuffer("");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
SizeBalancedTreeMap<String, Integer> sbt = new SizeBalancedTreeMap<String, Integer>();
sbt.put("d", 4);
sbt.put("c", 3);
sbt.put("a", 1);
sbt.put("b", 2);
// sbt.put("e", 5);
sbt.put("g", 7);
sbt.put("f", 6);
sbt.put("h", 8);
sbt.put("i", 9);
sbt.put("a", 111);
System.out.println(sbt.get("a"));
sbt.put("a", 1);
System.out.println(sbt.get("a"));
for (int i = 0; i < sbt.size(); i++) {
System.out.println(sbt.getIndexKey(i) + " , " + sbt.getIndexValue(i));
}
printAll(sbt.root);
System.out.println(sbt.firstKey());
System.out.println(sbt.lastKey());
System.out.println(sbt.floorKey("g"));
System.out.println(sbt.ceilingKey("g"));
System.out.println(sbt.floorKey("e"));
System.out.println(sbt.ceilingKey("e"));
System.out.println(sbt.floorKey(""));
System.out.println(sbt.ceilingKey(""));
System.out.println(sbt.floorKey("j"));
System.out.println(sbt.ceilingKey("j"));
sbt.remove("d");
printAll(sbt.root);
sbt.remove("f");
printAll(sbt.root);
}
}
4、SB树存在的意义
Java系统自带的有序表TreeMap、TreeSet底层是使用红黑树实现的,它们提供了一些功能,但是如果需要“查找 ≤ K \le K ≤K 的值有几个”这种功能就需要改写有序表,而这些系统没有的功能的改写仅仅是基于二叉搜索树,和SB树、AVL树没有人任何关系,为了更加高效,一般需要用到平衡型,而通常使用Size Balanced Tree 改写是最简单的。