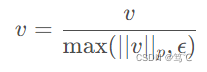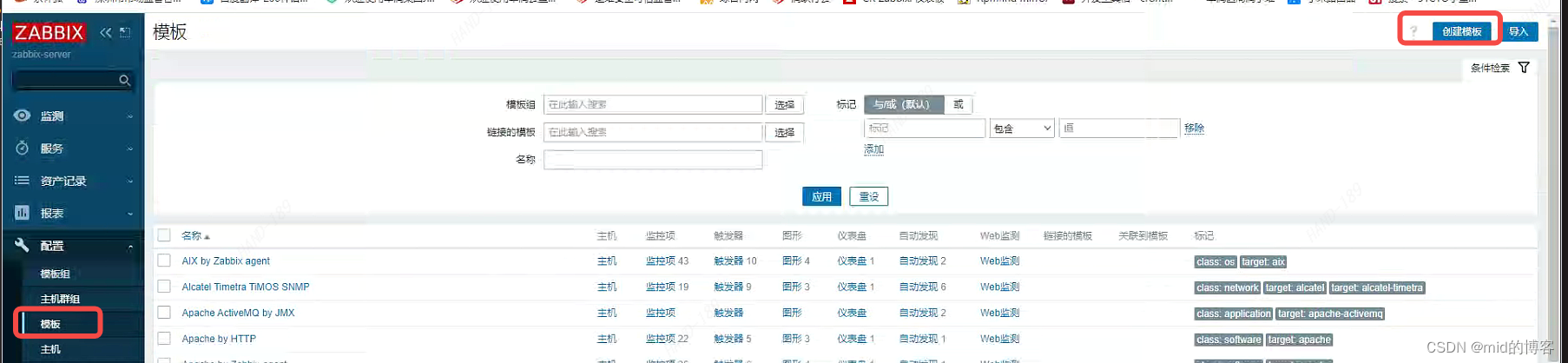
669 · 换硬币

669 · 换硬币
题目描述：
给出不同面额的硬币以及一个总金额. 写一个方法来计算给出的总金额可以换取的最少的硬币数量. 如果已有硬币的任意组合均无法与总金额面额相等, 那么返回 -1。

样例1
输入：
[1, 2, 5]
11
输出： 3
解释： 11 = 5 + 5 + 1

样例2
输入：
[2]
3
输出： -1

样例3
输入：
[1, 9]
0
输出： 0

举例：有面值为2，5，7三种硬币，找出能够使用最少硬币组合成总额为27的方案？

首先来看看使用递归的问题——做了很多重复计算，效率低下
在这里插入图片描述

在这里插入图片描述

public class Solution {
    /**
     * @param coins: a list of integer
     * @param amount: a total amount of money amount
     * @return: the fewest number of coins that you need to make up
     */
    public int coinChange(int[] coins, int amount) {
        int num = coins.length; //the num of given coins
        int[] f = new int[amount+1]; //0...amount
        f[0] = 0; //init
        for (int remainValue = 1; remainValue <= amount; remainValue++) {
            f[remainValue] = Integer.MAX_VALUE;
            //select last coin(each choice will consider n coins)
            for (int i = 0; i < num; i++) {
                if (remainValue >= coins[i] && f[remainValue-coins[i]] != Integer.MAX_VALUE && f[remainValue-coins[i]]+1<f[remainValue]) {
                    f[remainValue] = f[remainValue-coins[i]]+1;
                }
            }
        }
        if (f[amount] == Integer.MAX_VALUE) {
            return -1;
        }
        return f[amount];
    }
}

感觉数组下标还是用i，j比较直观，具体含义心中有数即可。

114 · 不同的路径

114 · 不同的路径
题目描述：
有一个机器人位于一个 m×n 网格的左上角。

机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。

问有多少条不同的路径？

样例 1：
输入：
n = 1
m = 3
输出：
1
解释：
只有一条通往目标位置的路径。

样例 2：
输入：
n = 3
m = 3
输出：
6
解释：
D : Down
R : Right
DDRR
DRDR
DRRD
RRDD
RDRD
RDDR
在这里插入图片描述

在这里插入图片描述

public class Solution {
    /**
     * @param m: positive integer (1 <= m <= 100)
     * @param n: positive integer (1 <= n <= 100)
     * @return: An integer
     */
    public int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        int i, j;
        // row traversal
        for (i = 0; i < m; i++) {
            //column traversal
            for (j = 0; j < n; j++) {
                if (i == 0 || j == 0) { //corner case
                    f[i][j] = 1;
                }else {
                	//           up           left        
                    f[i][j] = f[i-1][j] + f[i][j-1];
                }
            }
        }
        return f[m-1][n-1];
    }
}

116 · 跳跃游戏

116 · 跳跃游戏
题目描述：
给出一个非负整数数组，你最初定位在数组的第一个位置。

数组中的每个元素代表你在那个位置可以跳跃的最大长度。

判断你是否能到达数组的最后一个位置。

注：数组中的元素代表着青蛙在当前石头能跳的最大距离，而不是说一定要跳这么多。

样例 1：
输入：
A = [2,3,1,1,4]
输出：
true
解释：
0 -> 1 -> 4（这里的数字为下标）是一种合理的方案。

样例 2：
输入：
A = [3,2,1,0,4]
输出：
false
解释：
不存在任何方案能够到达终点。
在这里插入图片描述

public class Solution {
    /**
     * @param a: A list of integers
     * @return: A boolean
     */
    public boolean canJump(int[] a) {
        if (a == null || a.length == 0) {
            return false;
        }

        int n = a.length;
        boolean[] f = new boolean[n];
        //init
        f[0] = true;

        for (int j = 1; j < n; j++) {
            //previous stone(last step)
            f[j] = false;
            for (int i = 0; i < j; i++) {
                if (f[j] && i+a[i] >= j) {
                    f[j] = true;
                    break;
                }
            }
        }
        return f[n-1];
    }
}