目录
一、概念
1.1相关概念
1.2用途
1.3数据要求:独立性/正态性/方差齐性
1.4步骤
编辑1.5专业名词
二、基于python的单因素方差分析
2.2单因素方差分析的作用
一、概念
1.1相关概念
单因素方差分析是一种常用的统计分析方法,它用于比较一个因素对于连续性变量的影响。它通常用于研究一个自变量对一个因变量的影响,并比较不同组之间的均值是否显著不同。
在单因素方差分析中,数据被分成多个组,每个组都有自己的均值和方差。该方法基于比较这些组之间的方差来确定它们是否来自同一个总体。如果方差差异很小,则我们可以假定它们来自同一个总体,反之,则我们可以得出结论,这些组之间有显著的差异。
单因素方差分析通常用于实验设计,特别是在需要比较多个处理组时。该方法还可以用于比较不同组的表现,例如比较不同班级的平均分数或比较不同治疗方案的疗效。
单因素方差分析的假设包括:各组数据来自正态分布总体、各组方差相等、各组之间相互独立。该方法可以使用统计软件进行分析。常用的单因素方差分析方法包括单因素方差分析和方差齐性检验、多重比较方法(例如Tukey方法)等。
1.2用途
用来研究一个控制变量的不同水平是否对观测变量产生了显著影响。
人话:比较不同组别的平均值有无差异, 只有一个因素发生变化
原理:用来计算组间差异与组内差异的比值
若组间差异与组内差异的对比比值较大,则认为单因素方差分析的结果显著。即意味着不同组别的均值存在显著差异
1.3数据要求:独立性/正态性/方差齐性
1.因变量要为连续数值型变量,即共用一个坐标轴,可以取到任何数值
2.每一组对的变量都需要服从正态分布(可放宽)
3.组别间的方差相等(可放宽)
4.组别个数≥3组
1.4步骤
现在假定一个因素B具有c个水平的因变量进行方差分析检验,例如上面提到的工厂轧制设备是因素,分别试验轧制了10块板材是水平。
 1.5专业名词
1.5专业名词

听不懂吧,上例题
二、基于python的单因素方差分析
2.1所用库
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmstatsmodels是一个Python包,它为scipy提供了对scipy的补充。 统计计算,包括描述性统计和估计 以及统计模型的推理。
import numpy as np
from scipy import stats
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 生成示例数据,有3个组,每个组有5个观测值
group1 = [10, 12, 14, 15, 18]
group2 = [8, 9, 11, 14, 16]
group3 = [6, 7, 9, 12, 14]
# 将数据合并成一个数组
data = np.array(group1 + group2 + group3)
# 根据组信息创建因子
factors = np.array(['group1'] * 5 + ['group2'] * 5 + ['group3'] * 5)
# 执行单因素方差分析
F, p = stats.f_oneway(group1, group2, group3)
# 输出ANOVA结果
print('F值:', F)
print('p值:', p)
# 使用statsmodels创建ANOVA表
model = ols('data ~ factors', data=dict(data=data, factors=factors)).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table)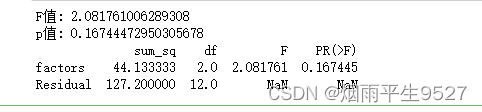
anova_lm是Python中statsmodels包中的函数,用于执行方差分析(ANOVA)并返回方差分析表的结果。该函数返回的参数包括:
df:自由度的数量,即方差分析中每个因素和误差的自由度。
sum_sq:平方和,即方差分析中每个因素和误差的平方和。
mean_sq:均方,即平方和除以相应的自由度,用于计算方差。
F:F统计量,即均方之比,用于检验因素是否显著影响结果变量。
PR(>F):p值,即F统计量的概率,用于检验因素是否显著影响结果变量。
eta_sq:方差解释比,即因素对总方差的解释程度。
omega_sq:Omega方差解释比,是对方差解释比的修正,考虑了样本量和自由度的影响。
此外,anova_lm还可以返回resid和resid_std,它们分别代表残差和标准化残差。
在方差分析中,我们可以使用PR值(p-value)来检测因素是否对结果变量具有显著影响。PR值是在假定因素对结果变量没有影响的情况下,观察到的数据样本出现当前统计结果或更极端结果的概率。
具体地,PR值是在计算F统计量之后,利用F分布的概率密度函数来计算得出的。我们将计算得到的F统计量与F分布进行比较,得到一个概率值(PR值),该值表明了出现这样极端的F统计量的概率。如果PR值小于显著性水平(通常为0.05),则我们可以拒绝假设,认为因素对结果变量具有显著影响。
需要注意的是,PR值只能告诉我们我们是否可以拒绝假设,不能证明假设成立。此外,PR值只能在当前样本中进行统计推断,并不代表总体情况。因此,在进行实验设计和数据分析时,我们需要合理设计样本,以增强推论的可靠性。残差(residual)指的是实际观测值与模型预测值之间的差异或偏差。在回归分析中,残差是因变量和自变量之间的线性关系无法完全解释因变量的部分,也可以理解为模型中未被解释的部分。残差是一个重要的概念,因为它们提供了评估模型拟合程度的一种方法。
2.2单因素方差分析的作用
单因素方差分析(One-way ANOVA)是一种用于比较三个或更多组均值是否相等的统计方法。在单因素方差分析中,我们将数据分成多个组,并将每个组的均值与整体均值进行比较,以确定组间差异是否显著。
单因素方差分析的作用在于:
确定不同组之间的均值是否有显著差异。单因素方差分析可以帮助我们确定组间差异是否显著,以及哪些组之间存在显著差异。这有助于我们更好地了解数据,并提供了可能的解释。
确定误差的大小。单因素方差分析可以帮助我们评估数据的可靠性,通过计算组间方差和误差方差来确定误差的大小。较小的误差可能表明数据更加一致和可靠,而较大的误差可能表明数据存在更多的随机误差或测量误差。
选择适当的统计测试。单因素方差分析可以帮助我们确定是否需要使用其他的统计方法来处理数据。例如,如果组间差异不显著,我们可以使用t检验来比较两个组之间的差异;如果组间差异显著,我们可以使用多重比较或后续分析来确定哪些组之间存在显著差异。
提供基础数据分析的统计框架。单因素方差分析是基本的数据分析方法之一,可以提供基本的统计框架和思考方式,有助于我们更好地理解其他复杂的数据分析技术。