---

前言

本篇文章将带领大家学习 冒泡排序 和 快速排序，它俩都属于交换排序。

1. 冒泡排序

🍑 基本思想

冒泡排序的英文Bubble Sort，是一种最基础的交换排序。

大家一定都喝过汽水，汽水中常常有许多小小的气泡，哗啦哗啦飘到上面来。这是因为组成小气泡的二氧化碳比水要轻，所以小气泡可以一点一点向上浮动。

而我们的冒泡排序之所以叫做冒泡排序，正是因为这种排序算法的每一个元素都可以像小气泡一样，根据自身大小，一点一点向着数组的一侧移动。

🍑 图解冒泡

假设有下面一组无序数组，我们要对它进行升序排序，具体实现过程如下：

第一趟冒泡排序的过程

按照冒泡排序的思想，我们要把相邻的元素两两比较，根据大小来交换元素的位置，过程如下：

首先让 6 和 9 比较，发现 6 比 9 要小，因此元素位置不变。

接下来让 9 和 7 比较，发现 9 比 7 要大，所以 9 和 7 交换位置。

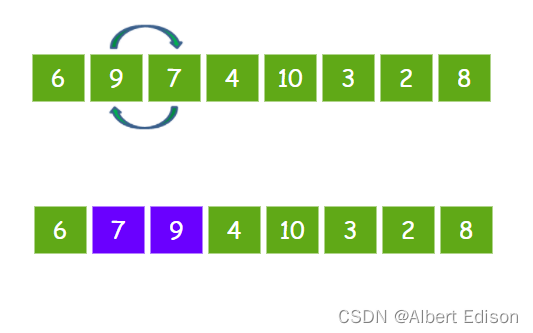
继续让 9 和 4 比较，发现 9 比 4 要大，所以 9 和 4 交换位置。

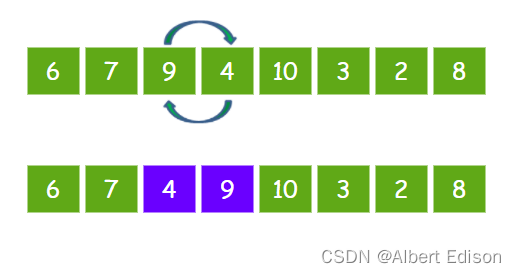
继续让 9 和 10 比较，发现 9 比 10 要小，所以元素位置不变。

接下来让 10 和 3 比较，发现 10 比 3 要大，所以 10 和 3 交换位置。

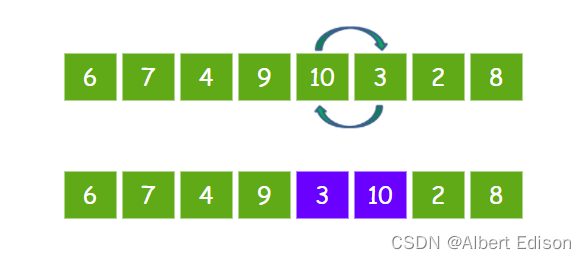
接下来让 10 和 2 比较，发现 10 比 2 要大，所以 10 和 2 交换位置。

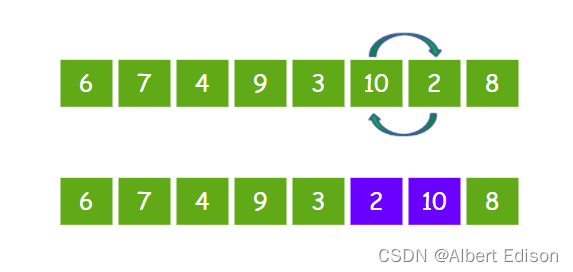
最后让 10 和 8 比较，发现 10 比 8 要大，所以 10 和 8 交换位置。

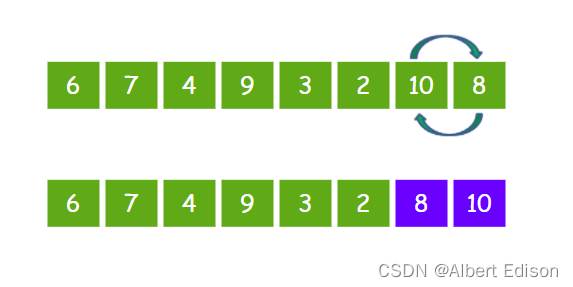
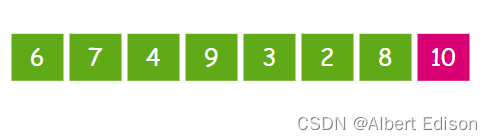
这样一来，元素 10 作为数列的最大元素，就像是汽水里的小气泡一样漂啊漂，漂到了最右侧。

这时候，我们的冒泡排序的第一轮结束了。数列最右侧的元素 10 可以认为是一个有序区域，有序区域目前只有一个元素。

第二趟冒泡排序的过程

下面，让我们来进行第二轮排序：

首先让 6 和 7 比较，发现 6 比 7 要小，因此元素位置不变。

接下来让 7 和 4 比较，发现 7 比 4 要大，所以 7 和 4 交换位置。

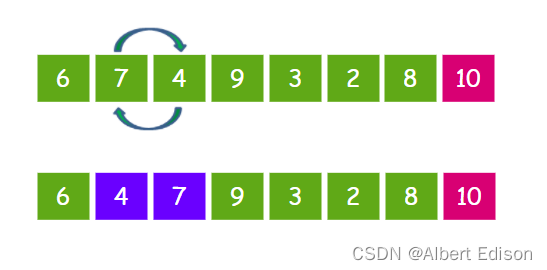
继续让 7 和 9 比较，发现 7 比 9 要小，因此元素位置不变。

接下来让 9 和 3 比较，发现 9 比 3 要大，所以 9 和 3 交换位置。

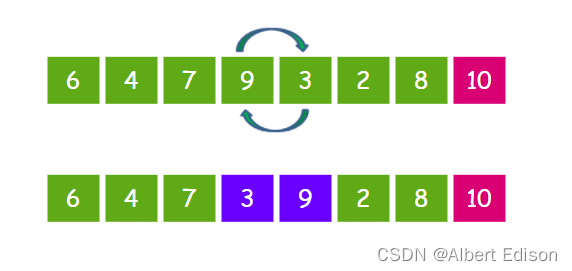
接下来让 9 和 2 比较，发现 9 比 2 要大，所以 9 和 2 交换位置。

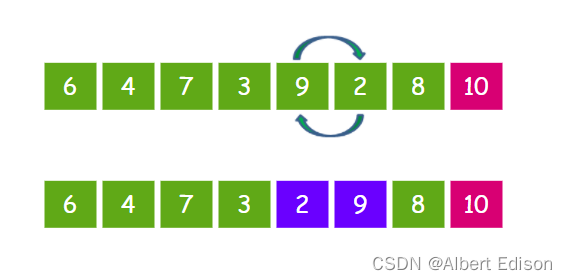
继续让 9 和 8 比较，发现 9 比 8 要大，所以 9 和 8 交换位置。

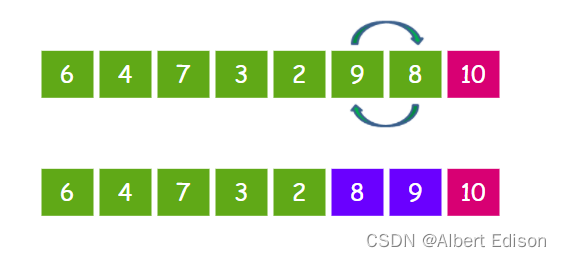
第二轮排序结束后，我们数列右侧的有序区有了两个元素，顺序如下：

第三趟冒泡排序的过程

按照以上步骤，第三轮过后的状态如下：

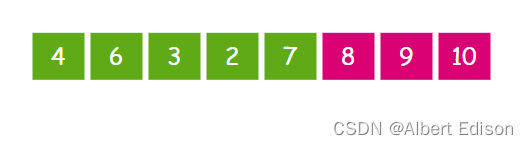
第四趟冒泡排序的过程

第四轮过后状态如下：

第五趟冒泡排序的过程

第五轮过后状态如下：

第六趟冒泡排序的过程

第六轮过后状态如下：

第七趟冒泡排序的过程

第七轮过后状态如下（已经是有序了，所以没有改变）：

第八趟冒泡排序的过程

第八轮过后状态如下（同样没有改变）：

到此为止，所有元素都是有序的了，这就是冒泡排序的整体思路。

🍑 动图演示

清楚了冒泡排序的过程，我们再来看一个动态图

🍑 代码实现

代码示例

//交换函数
void Swap(int* pa, int* pb) {
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

//冒泡排序
void BubbleSort(int* a, int n) {
	for (int j = 0; j < n; ++j) {
		//单趟
		for (int i = 1; i < n - j; ++i) {
			//前一个数大于后一个数，就交换
			if (a[i - 1] > a[i]) {
				Swap(&a[i - 1], &a[i]);
			}
		}
	}
}

🍑 代码优化

让我们回顾一下刚才描述的排序细节，仍然以 6,9,7,4,10,3,2,8 这个数组为例；

当排序算法分别执行到第六、第七、第八轮的时候，数列状态如下：

很明显可以看出，自从经过第六轮排序，整个数列已然是有序的了。可是我们的排序算法仍然 “兢兢业业” 地继续执行第七轮、第八轮。

这种情况下，如果我们能判断出数列已经有序，并且做出标记，剩下的几轮排序就可以不必执行，提早结束工作。

优化的思路是：如果能判断出数列已经是有序的了，并且做出标记，那么就不会执行多余的排序。

因此，我们进行一个优化的方法：就是设置一个 flag

如果在本轮排序中有元素进行交换，则说明数列无序，如果已经排序了那么设置为 0；
 
如果在本轮排序中，没有元素进行交换，则说明数列有序，那么设置为 1。

代码升级

//交换函数
void Swap(int* pa, int* pb) {
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

void BubbleSort(int* a, int n) {
	for (int j = 0; j < n; ++j) {
		int flag = 0; //记录该趟冒泡排序是否进行过交换
		//单趟
		for (int i = 1; i < n - j; ++i) {
			//前一个数大于后一个数，就交换
			if (a[i - 1] > a[i]) {
				flag = 1;
				Swap(&a[i - 1], &a[i]);
			}
		}
		if (0 == flag) { //该趟冒泡排序没有进行过交换，已有序
			break;
		}
	}
}

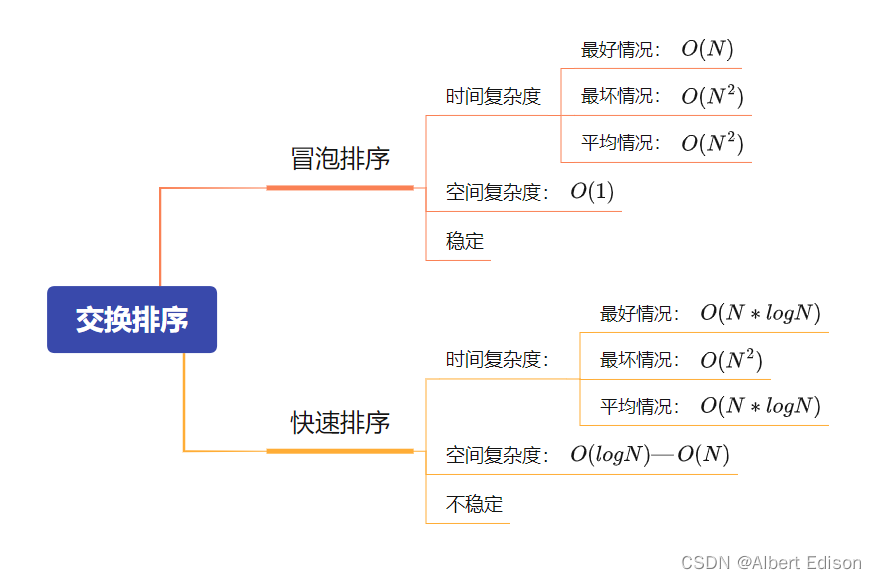
🍑 特性总结

（1）冒泡排序是一种非常容易理解的排序

（2）时间复杂度：$O(N^2)$

（3）空间复杂度：$O(1)$

（4）稳定性：稳定

2. 快速排序

快速排序是 Hoare 于 1962年 提出的一种二叉树结构的交换排序方法。

其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

将区间按照基准值划分为左右两半部分的常见方式有：

（1）hoare 版本

（2）挖坑法

（3）前后指针法

🍑 hoare 版本

Hoare 版本的单趟排序的基本步骤如下：

1）选出一个 key，一般是最左边或是最右边的指。
 
2）定义一个 L 指向最左边的位置，定义一个 R 指向最右边的位置，L 从左向右走，R 从右向左走。（需要注意的是：若选择最左边的数据作为 key，则需要 R 先走；若选择最右边的数据作为 key，则需要 L 先走）。
 
3）我们以选取最左边的值作为 key 为例子，那么 R 先走，在走的过程中，若 R 遇到小于 key 的数，则停下，L 开始走，直到 L 遇到一个大于 key 的数时，将 L 和 R 的内容交换，R 再次开始走，如此进行下去，直到 L 和 R 最终相遇，此时将相遇点的内容与 key 交换即可。
 
经过一次单趟排序，最终使得 key 左边的数据全部都小于 key，key 右边的数据全部都大于 key。

这个方法的精华在于：单趟排完以后，key 已经放在正确的位置，那么左边有序，右边有序，那么我们整体就有序了

🍅 图解过程

假设我们有下面这样一组无序数组，我们选择最左边的值作为 key，然后 L 指向最左边，R 指向最右边：

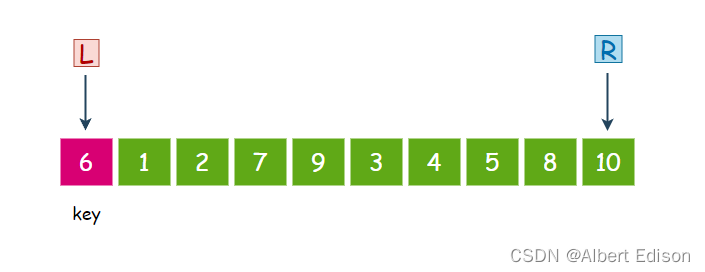
第一趟排序

首先，R 先走，从右往左找比 key 小的值，第一个数 10 大于 6，继续走。

第二个数 8 大于 6，继续走。

第三个数 5 小于 6，那么就停下来

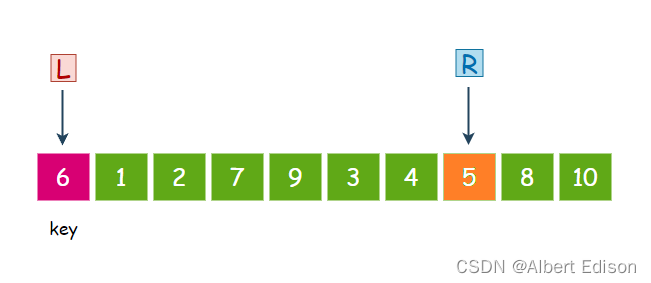
此时，L 开始走，从左往右找比 key 大的值，第一个数 1 小于 6，继续走。

第二个数，2 小于 6，继续走。

第三个数，7 大于 6，那么就停下来。

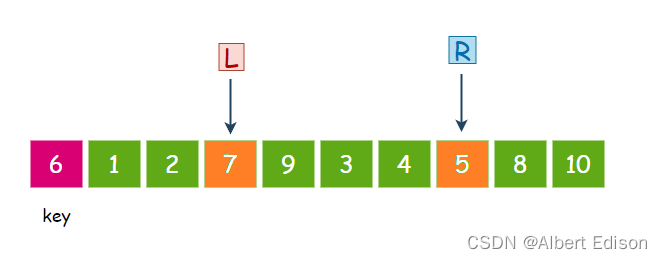
此时交换 L 和 R 指向的内容，也就是 5 和 7 交换：

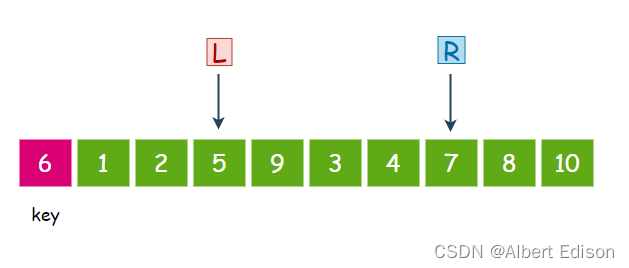
此时，R 再次移动，继续找比 key 小的值，4 小于 6，那么 R 就停下来：

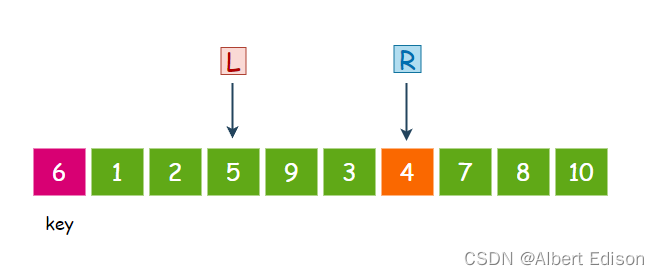
接着，L 再次移动，找比 key 大的值，9 大于 6，那么 L 就停下来：

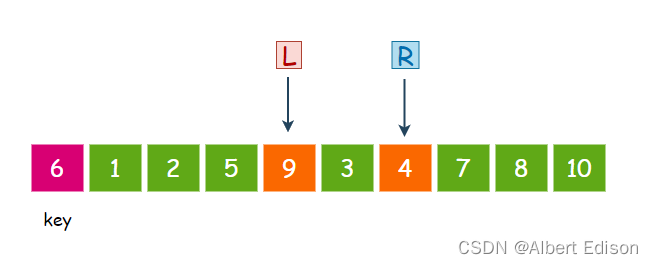
此时交换 L 和 R 指向的内容，也就是 4 和 9 交换：

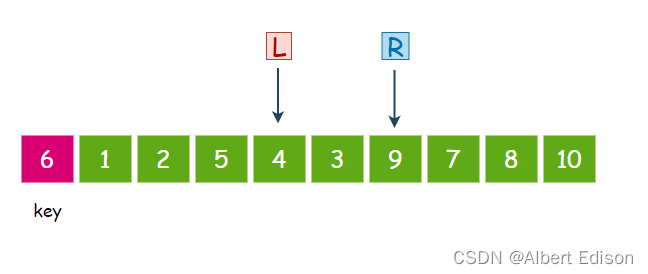
然后，R 再次移动，继续找比 key 小的值，3 小于 6，那么 R 就停下来：

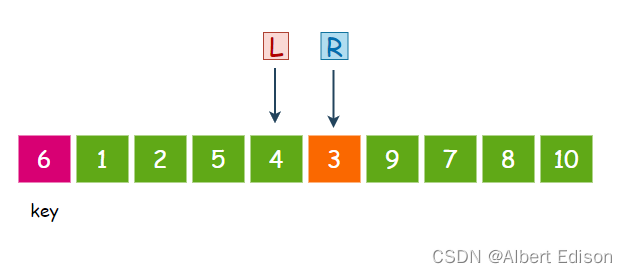
接着，L 再次移动，找比 key 大的值，注意，此时 L 向后走了一步以后，就和 R 相遇了

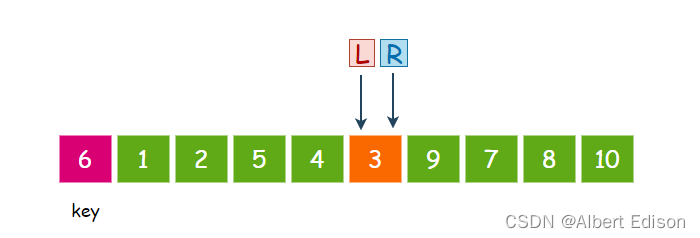
此时，直接把相遇位置的值和 key 交换，然后我们可以发现，这一趟排序完成以后，6 已经回到了正确的位置上！

然后我们再将 key 的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作，因为这种序列可以认为是有序的。

🍅 动图演示

清楚了单趟 hoare 排序的过程，我们再来看一个动态图

🍅 代码实现

代码示例

/*
* 快速排序（hoare版本）
* 1.左边做key，那么右边先走
* 2.右边做key，那么左边先走
* 
* 单趟排完以后，key已经放在正确的位置
* 如果左边有序，右边有序，那么我们整体就有序了
* 那么左边和右边如何有序呢/
* 用分治的思想来解决子问题
*/

//交换函数
void Swap(int* pa, int* pb) {
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

//hoare单趟排序 --- 左边做key
int PartSort1(int* a, int left, int right) {
	int keyi = left; //左边做key，保存的是key的下标
	while (left < right) {
		//右边先走，找小
		//为什么用等于呢？如果keyi和right位置的值相等，那么就会出现死循环
		//为什么要加一个 left<right的条件呢？如果数组本身就是有序的，比如 1 2 3 4 5，那么right就会一直向左移动，并且会越界
		while (left < right && a[right] >= a[keyi]) {
			--right;
		}

		//左边后走，找大
		while (left < right && a[left] <= a[keyi]) {
			++left;
		}

		//然后交换左右
		Swap(&a[left], &a[right]);
	}
	//当left == right的时候，跳出循环，交换和keyi的值
	Swap(&a[keyi], &a[left]);

	//返回相遇位置的下标
	return left;
}

//快速排序递归实现的主框架
void QuickSort1(int* a, int begin, int end) {
	//子区间相等只有一个值，或者不存在，那么就是递归结束的子问题
	if (begin >= end) {
		return;
	}

	int keyi = PartSort1(a, begin, end);
	
	//递归左区间 [begin, keyi-1]
	QuickSort1(a, begin, keyi - 1);
	
	//递归右区间 [keyi+1, end]
	QuickSort1(a, keyi + 1, end);
}

//测试函数
int main()
{
	//创建数组
	int array[10] = { 9,1,2,5,7,4,8,6,3,10 };
	int sz = sizeof(array) / sizeof(array[0]);
	
	//快速排序-hoare版本
	QuickSort1(array, 0, sz - 1);
	
	return 0;
}

🍅 特性总结

时间复杂度：$O(N\ast logN)$

🍑 挖坑法

挖坑法的单趟排序的基本步骤如下：

1）选出一个数据（一般是最左边或是最右边的）存放在 key 变量中，在该数据位置形成一个坑。
 
2）定义一个 L 指向最左边的位置，定义一个 R 指向最右边的位置，L 从左向右走，R 从右向左走（若在最左边挖坑，则需要 R 先走；若在最右边挖坑，则需要 L 先走）。
 
3）假设我们这里选取最左边的作为坑位，那么就是 R 先走，在走的过程中，若 R 遇到小于 key 的数，则将该数放入坑位，并在此处形成一个坑位，这时 L 再向后走，若遇到大于 key 的数，则将其放入坑位，又形成一个坑位，如此循环下去，直到最终 L 和 R 相遇，这时将 key 放入坑位即可。
 
经过一次单趟排序，最终也使得 key 左边的数据全部都小于 key，key 右边的数据全部都大于key。

挖坑法相比于 hoare 法，更好理解：

1）不需要理解为什么最终相遇位置比 key 小
 
2）不需要理解为什么左边做key，右边先走

🍅 图解过程

假设我们有下面这样一组无序数组，我们选择最左边的值把它存放到变量 key 中，然后在该位置形成一个坑位，还是 L 指向最左边，R 指向最右边：

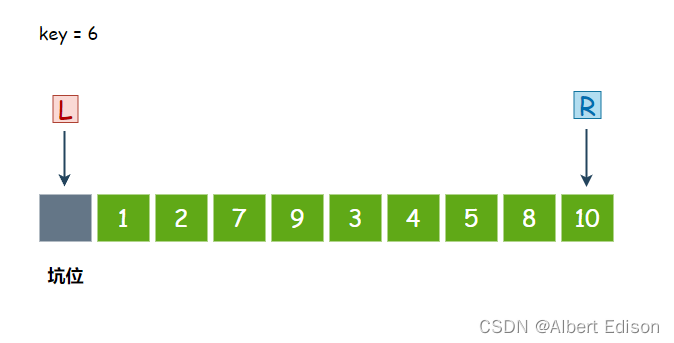
第一趟排序

首先，R 先走，从右往左找比 key 小的值，第一个数 10 大于 6，继续走。

第二个数 8 大于 6，继续走。

第三个数 5 小于 6，停下来，把 5 扔到坑位里面去，然后在 R 位置形成新的坑位：

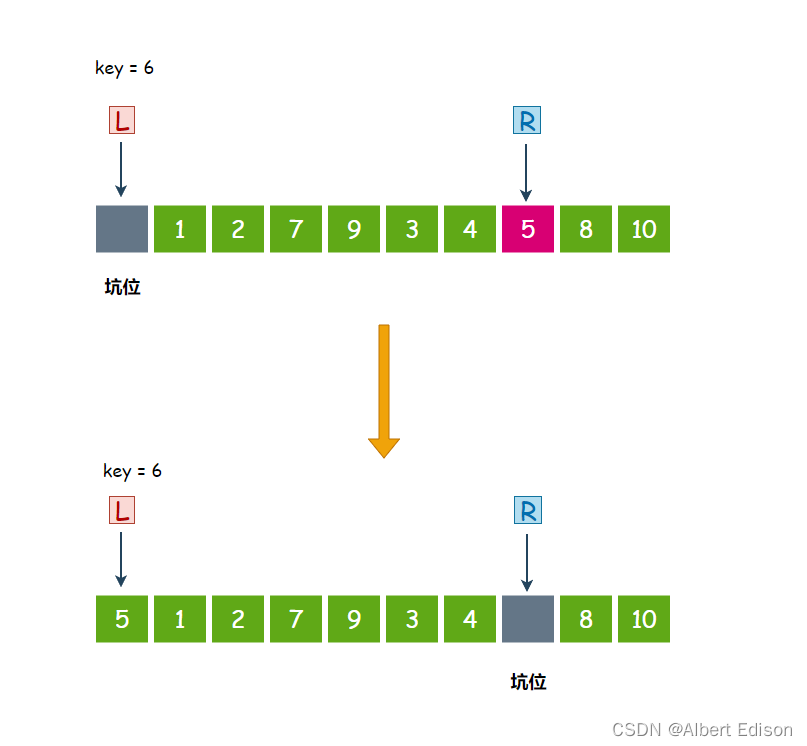
此时，L 开始走，从左往右找比 key 大的值，第一个数 1 小于 6，继续走。

第二个数 2 小于 6，继续走。

第三个数 7 大于 6，停下来，把 7 扔到坑位里面去，然后在 L 位置形成新的坑位：

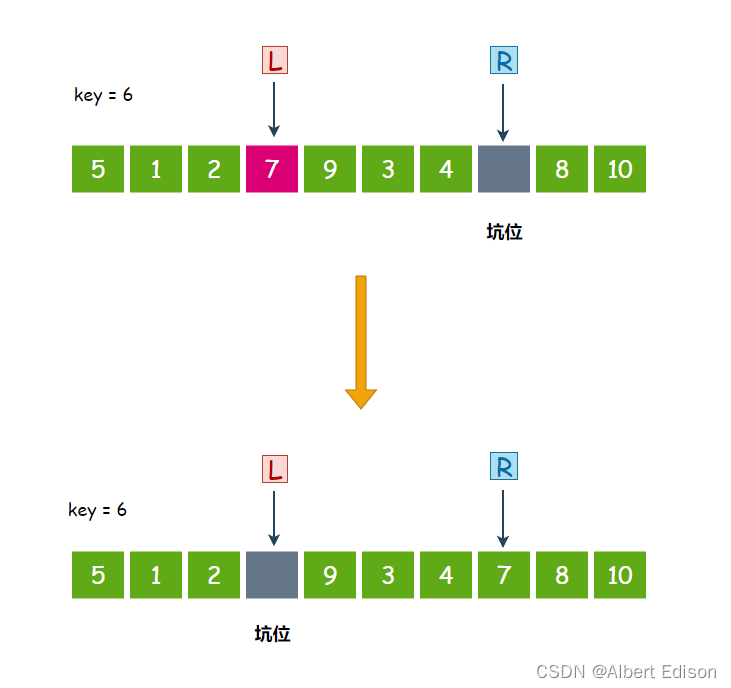
此时，R 开始走，从右往左找比 key 小的值，4 小于 6，停下来，把 4 扔到坑位里面去，然后在 R 位置形成新的坑位：

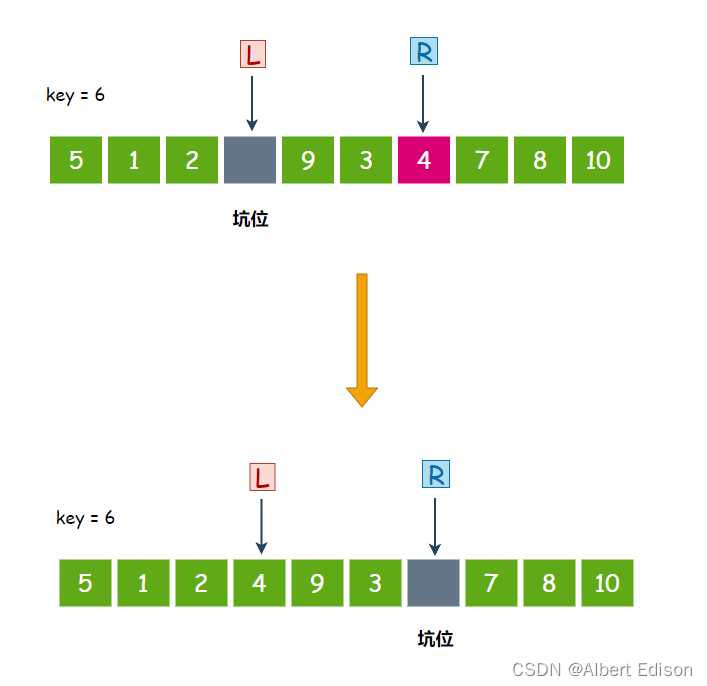
此时，L 开始走，从左往右找比 key 大的值，9 大于 6，停下来，把 9 扔到坑位里面去，然后在 L 位置形成新的坑位：

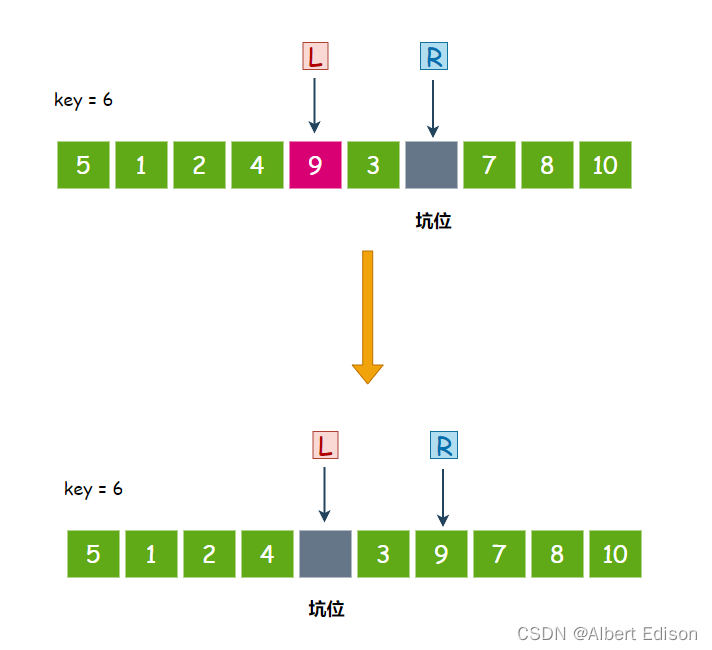
此时，R 开始走，从右往左找比 key 小的值，3 小于 6，停下来，把 3 扔到坑位里面去，然后在 R 位置形成新的坑位：

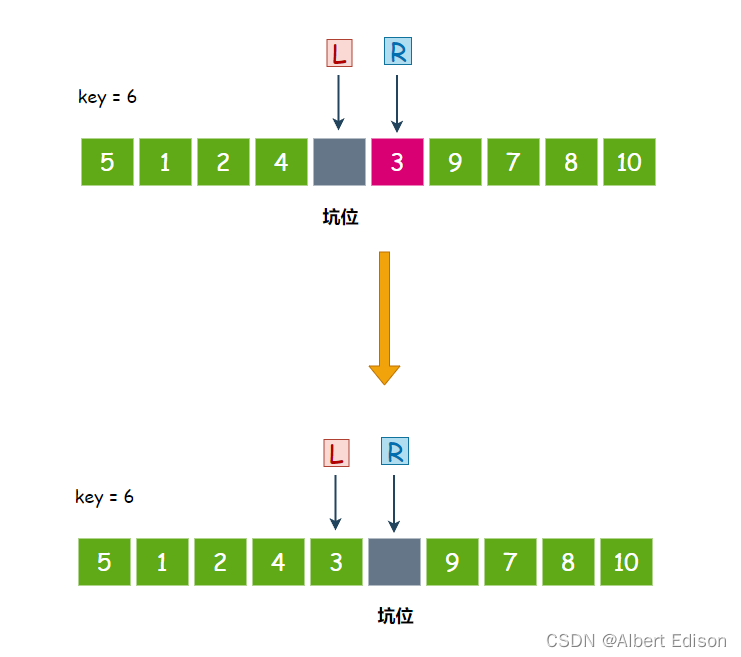
此时，L 开始向后走，走了一步以后，L 与 R 相遇了，那么直接把 key 存放的值放入该坑位中即可

可以看到 6 已经放到了正确的位置上面。

然后也是将 key 的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作。

🍅 动图演示

清楚了单趟挖坑法的过程，我们再来看一个动态图

🍅 代码实现

代码示例

//交换函数
void Swap(int* pa, int* pb) {
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

//挖坑法 --- 左边做key
int PartSort2(int* a, int left, int right) {
	int key = a[left]; //保存的是key的值
	int pit = left; //坑位
	while (left < right) {
		//右边先走，找小
		while (left < right && a[right] >= key) {
			--right;
		}
		//找到小的值以后，把小的值扔到左边的坑位上去
		a[pit] = a[right];
		pit = right; //此时right的位置就是新的坑位

		//左边后走，找大
		while (left < right && a[left] <= key) {
			++left;
		}
		//找到大的值以后，把大的值扔到坑位上去
		a[pit] = a[left];
		pit = left; //此时left的位置就是新的坑位
	}
	//循环结束以后，说明相遇了，相遇的位置就是坑位
	a[pit] = key; //把最开始保存的key放到相遇的坑位里面
	return pit; //返回key的下标
}

//快速排序递归实现的主框架
void QuickSort1(int* a, int begin, int end) {
	//子区间相等只有一个值，或者不存在，那么就是递归结束的子问题
	if (begin >= end) {
		return;
	}

	int keyi = PartSort2(a, begin, end);
	
	//递归左区间 [begin, keyi-1]
	QuickSort1(a, begin, keyi - 1);
	
	//递归右区间 [keyi+1, end]
	QuickSort1(a, keyi + 1, end);
}

//测试函数
int main()
{
	//创建数组
	int array[10] = { 9,1,2,5,7,4,8,6,3,10 };
	int sz = sizeof(array) / sizeof(array[0]);
	
	//快速排序-挖坑法
	QuickSort1(array, 0, sz - 1);
	
	return 0;
}

🍅 特性总结

时间复杂度：$O(N\ast logN)$

🍑 前后指针法

前后指针法的单趟排序的基本步骤如下：

1）选出一个 key，一般是最左边或是最右边的。
 
2）起始时，prev 指针指向序列开头，cur 指针指向 prev+1。
 
3.1）若 cur 指向的内容小于 key，则 prev 先向后移动一位，然后交换 prev 和 cur 指针指向的内容，然后 cur 指针 ++；
 
3.2）若 cur 指向的内容大于 key，则 cur 指针直接++。如此进行下去，直到 cur 指针越界，此时将 key 和 prev 指针指向的内容交换即可。
 
经过一次单趟排序，最终也能使得 key 左边的数据全部都小于 key，key 右边的数据全部都大于 key。

🍅 图解过程

初始时，prev 指向数组开头，cur 指向 prev+1 的位置，选择最左边的元素作为 key：

首先，cur 指向的元素是 1，小于 6，那么 prev 先往后走一步， 然后交换 prev 和 cur 指针指向的值，然后 cur 指针再往后走一步：

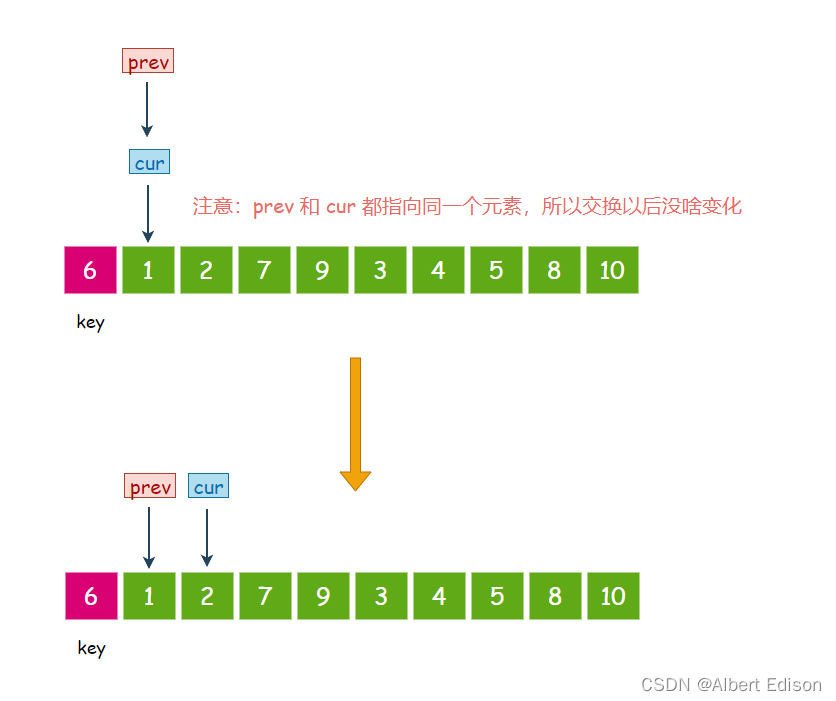
此时 cur 指向的元素是 2，小于 6，那么 prev 先往后走一步， 然后交换 prev 和 cur 指针指向的值，然后 cur 指针再往后走一步：

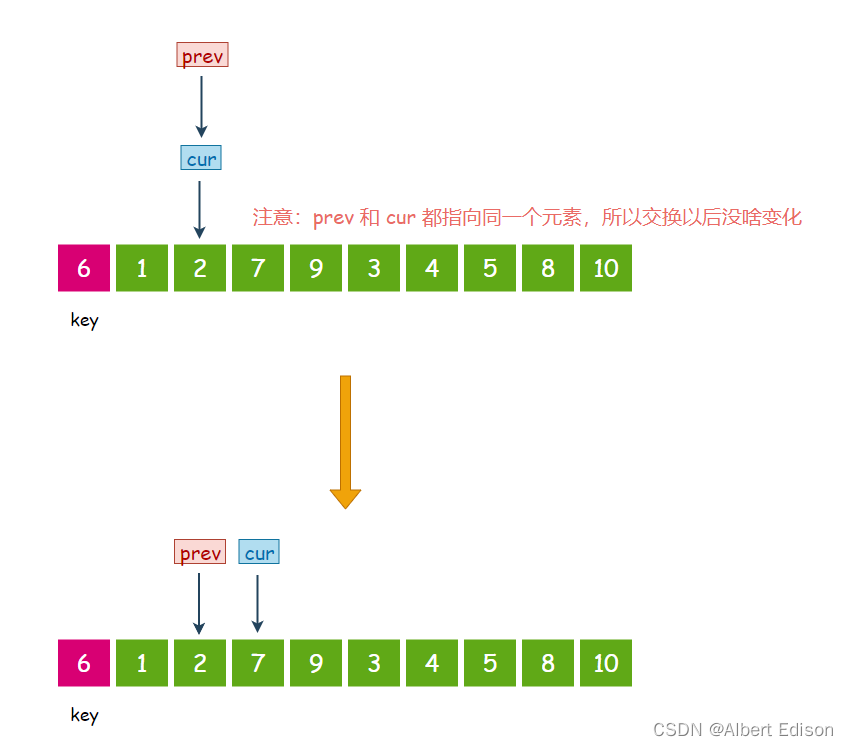
此时 cur 指向的元素是 7，大于 6，那么 cur 指针直接向后走一步，prev 指针不动。

接着 cur 又指向 9，大于 6，那么 cur 指针继续向后走一步，prev 指针还是不动。

此时 cur 指向 3，小于 6，那么 prev 先往后走一步， 然后交换 prev 和 cur 指针指向的值，然后 cur 指针再往后走一步：

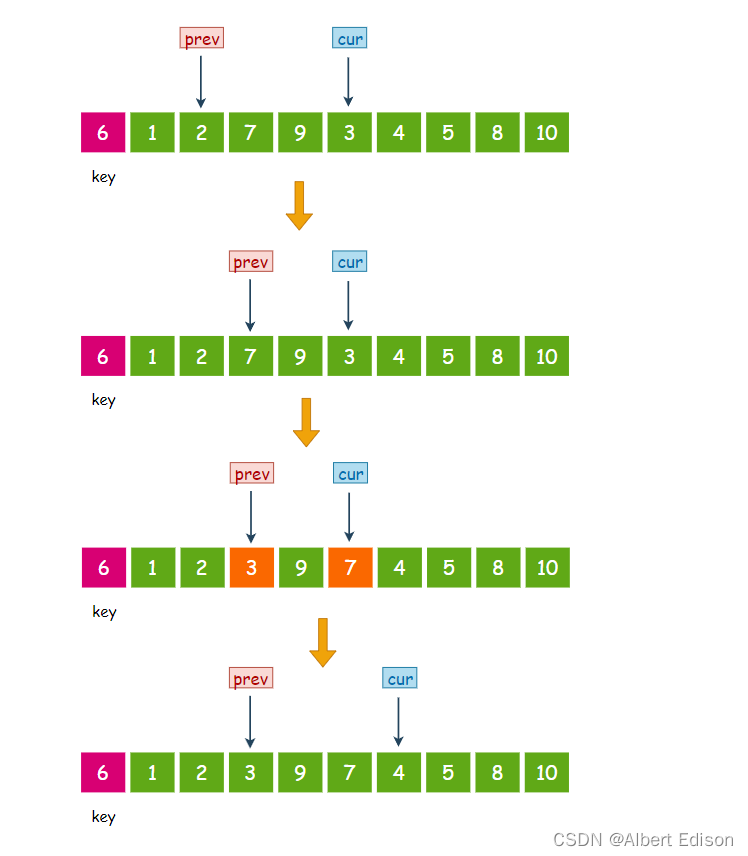
此时 cur 指向 4，小于 6，那么 prev 先往后走一步， 然后交换 prev 和 cur 指针指向的值，然后 cur 指针再往后走一步：

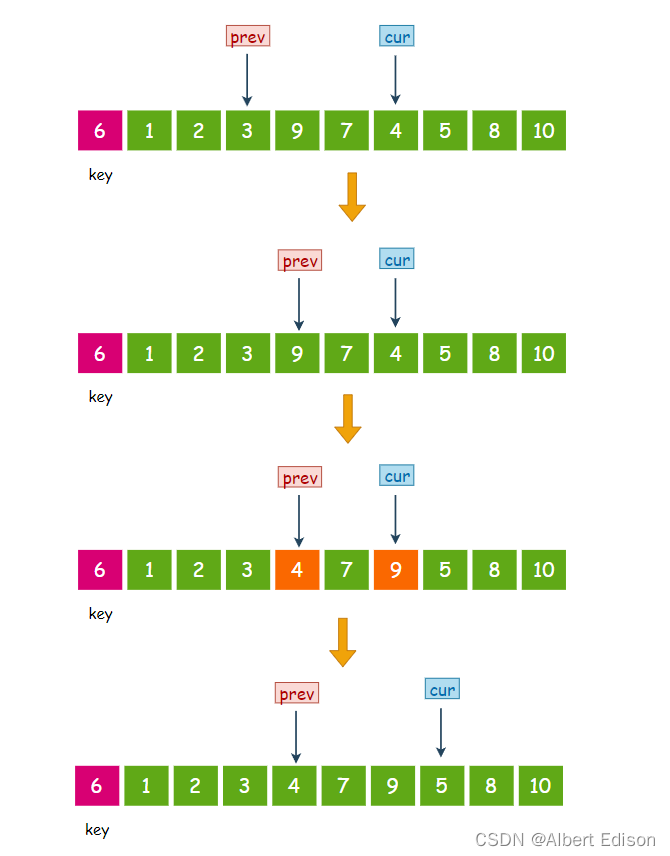
此时 cur 指向 5，小于 6，那么 prev 先往后走一步， 然后交换 prev 和 cur 指针指向的值，然后 cur 指针再往后走一步：

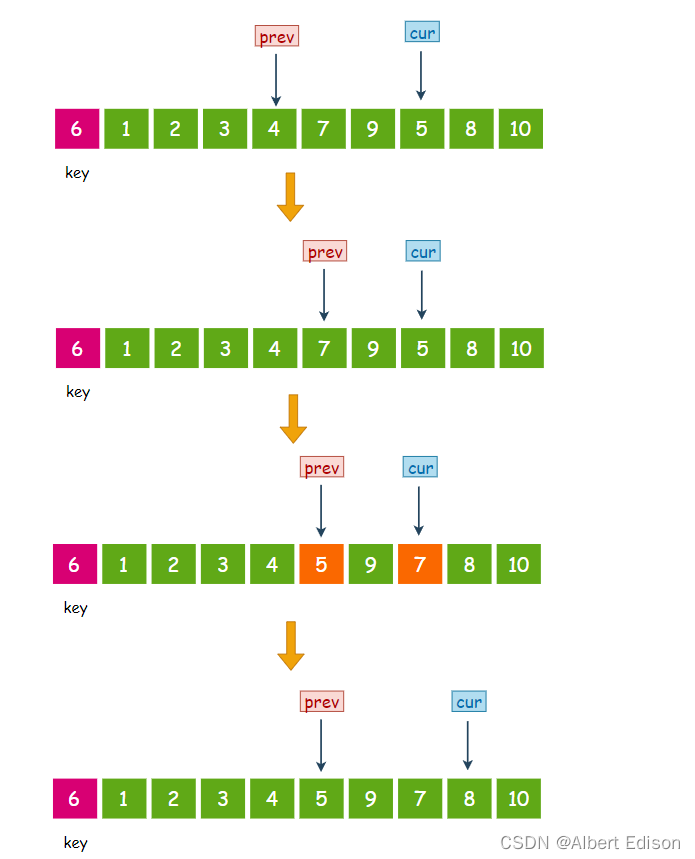
此时 cur 指向的元素 8 大于 6，那么 cur 指针直接向后走一步，prev 指针不动。

接着 cur 指向的元素 10 大于 6，那么 cur 指针直接向后走一步，prev 指针不动。

此时 cur 指针已经越界，那么我们将 prev 指向的元素 5 与 key 进行交换：

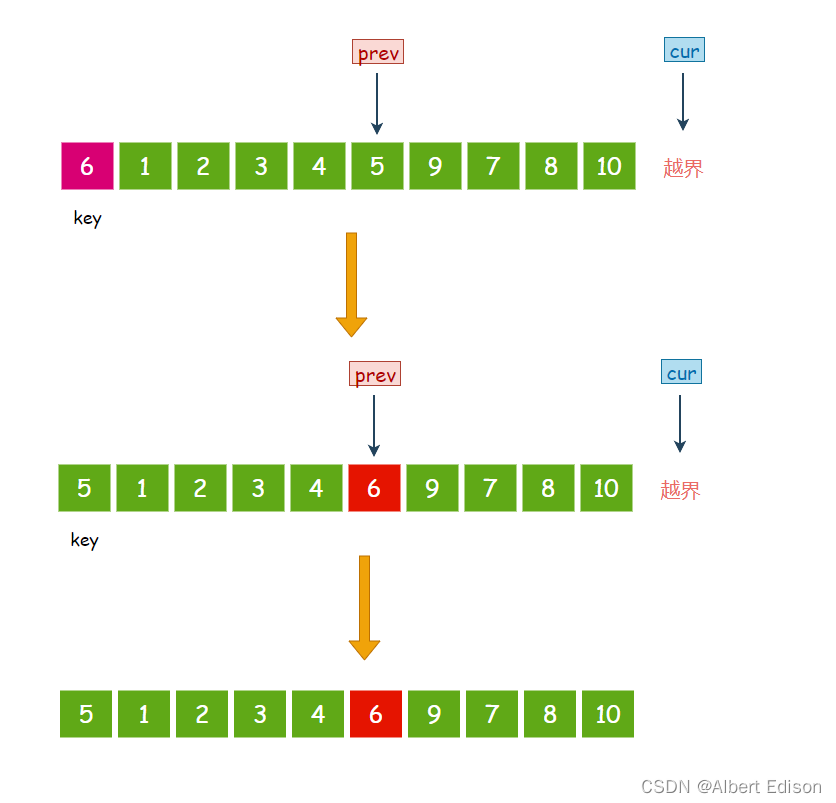
此时，元素 6 已经回到了正确的位置上面。

然后还是将 key 的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作。

🍅 动图演示

清楚了前后指针法的过程，我们再来看一个动态图

🍅 代码实现

代码示例

//交换函数
void Swap(int* pa, int* pb) {
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

//前后指针法 --- 左边做key
int PartSort3(int* a, int left, int right) {
	int keyi = left;
	int prev = left;
	int cur = left + 1;
	//闭区间
	while (cur <= right) {
		// ++的优先级比[]高，所以先++prev
		// cur遇到比key小的值以后，就++prev，如果prev和cur相等，那么就没必要交换，防止自己和自己交换
		// cur遇到比key小的值以后，就++prev，如果prev不等于cur，那么就把prev和cur位置的值交换
		if (a[cur] < a[keyi] && a[++prev] != a[cur]) {
			Swap(&a[prev], &a[cur]);
		}
		++cur;
	}
	Swap(&a[prev], &a[keyi]);

	return prev;
}

//快速排序递归实现的主框架
void QuickSort1(int* a, int begin, int end) {
	//子区间相等只有一个值，或者不存在，那么就是递归结束的子问题
	if (begin >= end) {
		return;
	}

	int keyi = PartSort3(a, begin, end);
	
	//递归左区间 [begin, keyi-1]
	QuickSort1(a, begin, keyi - 1);
	
	//递归右区间 [keyi+1, end]
	QuickSort1(a, keyi + 1, end);
}

//测试函数
int main()
{
	//创建数组
	int array[10] = { 9,1,2,5,7,4,8,6,3,10 };
	int sz = sizeof(array) / sizeof(array[0]);
	
	//快速排序-挖坑法
	QuickSort1(array, 0, sz - 1);
	
	return 0;
}

🍅 特性总结

时间复杂度：$O(N\ast logN)$

🍑 快速排序的优化

🍅 三数取中

在理想情况下，我们每次进行完单趟排序后，假设 key 的左序列与右序列的长度都相同，若每趟排序所选的 key 都正好是该序列的中间值，即单趟排序结束后 key 位于序列正中间，那么快速排序的时间复杂度就是 $O(NlogN)$。

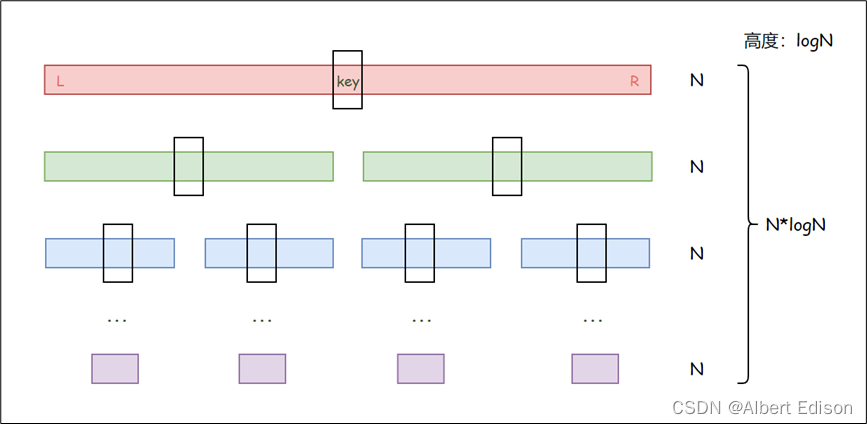
可是谁能保证你每次选取的 key 都是正中间的那个数呢？

假设，当待排序列本就是一个有序的序列时，我们若是依然每次都选取最左边或是最右边的数作为 key，那么快速排序的效率将达到最低：

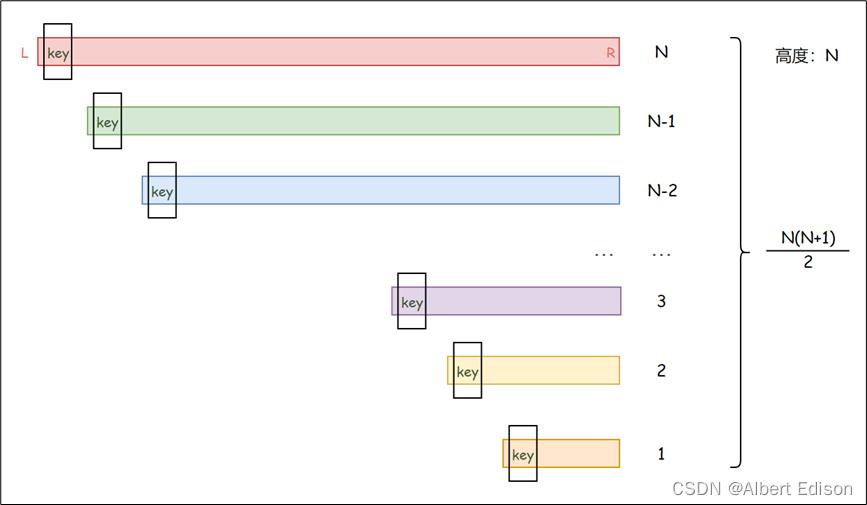
如上图所示，这种情况下，快速排序的时间复杂度退化为 $O(N^2)$。

其实，对快速排序效率影响最大的就是选取的 key，若选取的 key 越接近中间位置，则则效率越高。

为了避免这种极端情况的发生，于是出现了三数取中：

三数取中，当中的三数指的是：最左边的数、最右边的数以及中间位置的数。
 
三数取中就是取这三个数当中，值的大小居中的那个数作为该趟排序的 key。
 
这就确保了我们所选取的数不会是序列中的最大或是最小值了。

代码示例

//快排优化1 --- 比较最左边、最右边、最中间的三个数
//在这三个数中，去掉最大、去掉最小，选择中间的那个数
//然后把它和最左边或者最右边交换，做key
int GetMidIndex(int* a, int left, int right) {
	//如果left和right特别大，可能两个数一加，超过了整型的一半，就会溢出
	//所以选择移位
	int mid = left + ((right - left) >> 1);

	if (a[left] < a[mid]) {
		if (a[mid] < a[right]) {
			return mid;
		}
		else if (a[mid] > a[right]) {
			return left;
		}
		else {
			return right;
		}
	}
	else { // a[left] > a[mid]
		if (a[mid] > a[right]) {
			return mid;
		}
		else if (a[left] < a[right]) {
			return left;
		}
		else {
			return right;
		}
	}
}

/*
* 快速排序（前后指针法）
* 左边做key
*/
int PartSort3(int* a, int left, int right) {
	//三数取中找key
	int midi = GetMidIndex(a, left, right);
	Swap(&a[midi], &a[left]);

	int keyi = left;
	int prev = left;
	int cur = left + 1;
	//闭区间
	while (cur <= right) {
		// ++的优先级比[]高，所以先++prev
		// cur遇到比key小的值以后，就++prev，如果prev和cur相等，那么就没必要交换，防止自己和自己交换
		// cur遇到比key小的值以后，就++prev，如果prev不等于cur，那么就把prev和cur位置的值交换
		if (a[cur] < a[keyi] && a[++prev] != a[cur]) {
			Swap(&a[prev], &a[cur]);
		}
		++cur;
	}
	Swap(&a[prev], &a[keyi]);

	return prev;
}

注意：这个三数取中函数可以放在任意一个单趟排序版本中，上面代码我是放在了前后指针法的代码中。

🍅 小区间优化

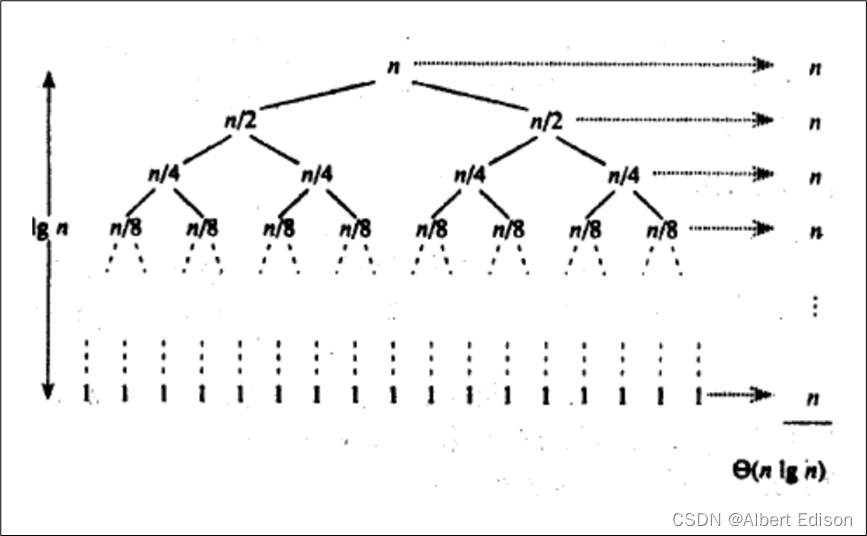
我们可以看到，就算是上面理想状态下的快速排序，也不能避免随着递归的深入，每一层的递归次数会以 2 倍的形式快速增长。

为了减少递归树的最后几层递归，我们可以在 快速排序的主体框架中 设置一个判断语句，当序列的长度小于某个数的时候就不再进行快速排序，转而使用其他种类的排序。

小区间优化若是使用得当的话，会在一定程度上 加快 快速排序的效率，而且待排序列的长度越长，该效果越明显。

代码示例

//插入排序
void InsertSort(int* a, int n) {
	//数组的长度是n，那么最后一个数据是n-1，倒数第二个数据是n-2
	for (int i = 0; i < n - 1; ++i) {
		// [0 end]有序，把end+1的位置的值插入进去，保持它依旧有序
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0) {
			if (tmp < a[end]) {
				a[end + 1] = a[end];
				--end;
			}
			else {
				break;
			}
		}
		//当end走到-1时，所有比它大的值都挪走了，所以直接放到下标为0的位置处
		a[end + 1] = tmp;
	}
}

/*快排优化2
* 快排递归调用展开就是一颗二叉树
* 区间很小时，不再使用递归划分的思路让他有序，而是直接使用插入排序对小区间排序，减少递归调用
*/
void QuickSort2(int* a, int begin, int end) {
	//子区间相等只有一个值，或者不存在，那么就是递归结束的子问题
	if (begin >= end) {
		return;
	}

	// 小区间直接插入排序控制有序
	if (end - begin + 1 <= 10) {
		InsertSort(a + begin, end - begin + 1); //当长度小于等于10时，使用插入排序
	}
	else {
		int keyi = PartSort3(a, begin, end); //这里使用的是前后指针法

		//递归左区间 [begin, keyi-1]
		QuickSort2(a, begin, keyi - 1);

		//递归右区间 [keyi+1, end]
		QuickSort2(a, keyi + 1, end);
	}
}

🍑 非递归实现

上面我们使用递归实现了快速排序的主框架，可以发现与二叉树前序遍历规则非常像，所以在写递归框架时可想想二叉树前序遍历规则即可快速写出来，后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。

如果在这里想把主框架改为非递归实现的话，那么需要借助前面学到的一种数据结构 栈，我们先来看一看非递归实现的思路：

1）先将待排序列的第一个元素的下标和最后一个元素的下标入栈。
 
2.1）当栈不为空时，读取栈中的信息（一次读取两个，一个是 L，另一个是 R），然后调用某一版本的单趟排序，排完后获得了 key 的下标，然后判断 key 的左序列和右序列是否还需要排序，若还需要排序，就将相应序列的 L 和 R 入栈；
 
2.2）若不需排序了（序列只有一个元素或是不存在），就不需要将该序列的信息入栈。
 
最好，反复执行步骤 2，直到栈为空为止。

🍅 代码实现

代码示例

//快速排序 --> 非递归
void QuickSort3(int* a, int begin, int end) {
	ST st; //创建栈
	StackInit(&st); //初始化栈
	StackPush(&st, begin); //待排序列的L
	StackPush(&st, end); //待排序列的R

	while (!StackEmpty(&st))
	{
		int right = StackTop(&st); //读取R
		STackPop(&st); //出栈
		int left = StackTop(&st); //读取L
		STackPop(&st); //出栈

		//该处调用的是前后指针版本的单趟排序
		int keyi = PartSort3(a, left, right);

		//该序列的左序列还需要排序
		if (left < keyi - 1) {
			StackPush(&st, left); //左序列的L入栈
			StackPush(&st, keyi - 1); //左序列的R入栈
		}
		//该序列的右序列还需要排序
		if (keyi + 1 < right) {
			StackPush(&st, keyi + 1); //右序列的L入栈
			StackPush(&st, right); //右序列的R入栈
		}
	}
	//销毁栈
	StackDestory(&st);
}

🍑 特性总结

（1）快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

（2）时间复杂度：$O(N\ast logN)$

（3）空间复杂度：$O(logN)$

（4）稳定性：不稳定

3. 总结