贪心算法

1. 局部最右得到全局最右
2. 难点在于如何证明局部最优可以得到全局最优
3. 堆 和 排序 是贪心算法最常用的实现算法

贪心算法作为最符合自然智慧的算法，思路是从小部分取最优从而获得最终的最优，但是难得是怎样获取部分最优才能得到全局最优。

有时候我们会有多个局部最优的想法（或者说局部最贪）但是很多时候这些都是陷阱。

如何验证我们的局部最优想法是对的是贪心算法最复杂的地方：

1. 数学逻辑推算验证 （太过耗时，费力不讨好）
2. 对数器验证 （推荐）

这里推荐使用对数器来进行验证，即写一个最傻的求解方法（如穷举可能性），与我们贪心算法进行验证。

如何想到贪心算法 这个似乎没有捷径，需要阅历经验和敏捷的思考，即多锻炼吧…………

最后抛两个例子

金条分隔问题

给一根长度为 n 的金条，分隔此金条长度为 x, y 两份(x+y =n) 需要和金条长度数值相同的 n 个铜币。

给定一个数组数组和为 n，问最小代价为多少。

例如：

金条长度为 80
给定数组 [50,20,10]
如果
分隔： 70 , 10 花费 80
分隔： 50 , 20 花费 70 总 150

相对平均分割
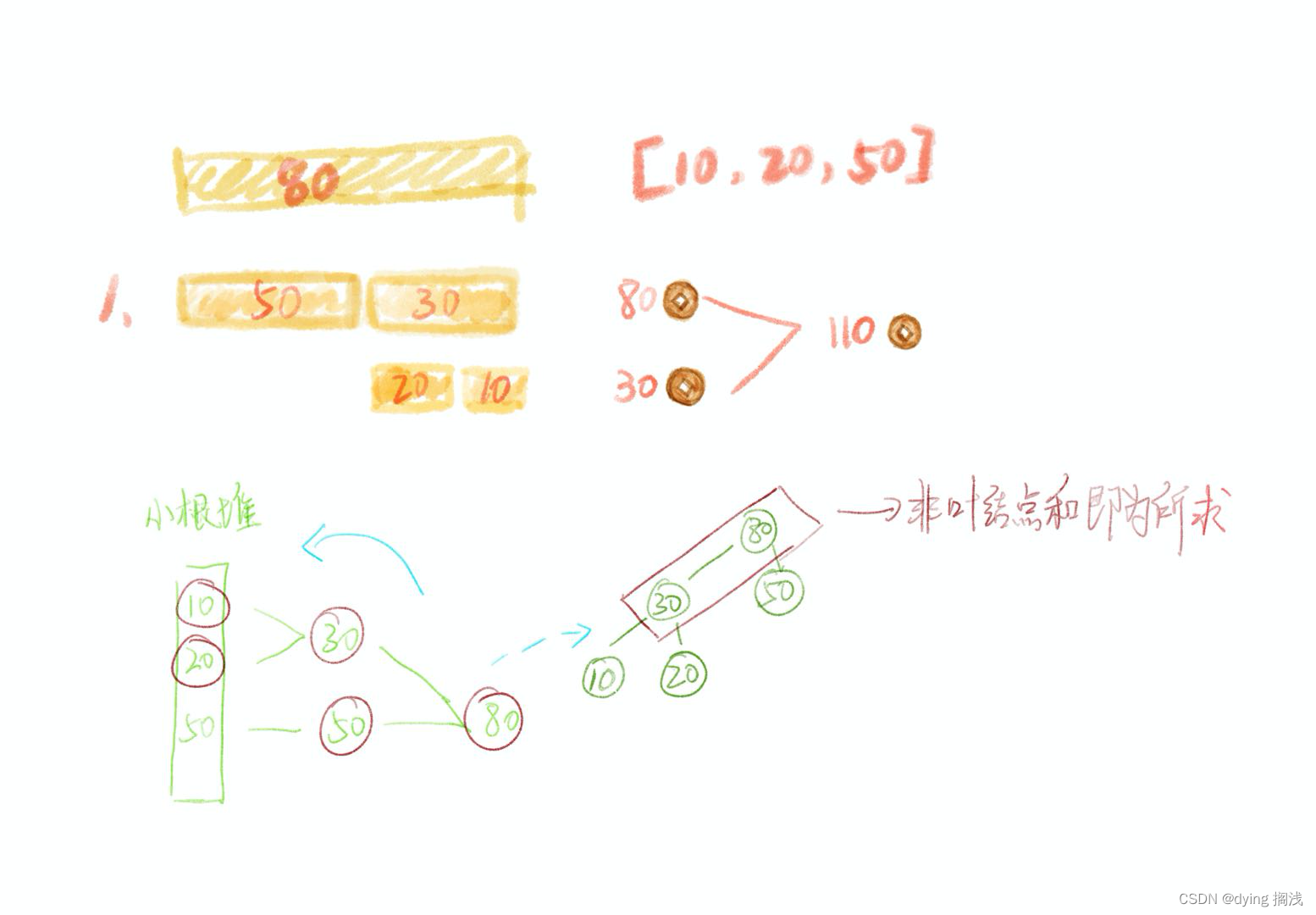
分隔： 50 , 30 花费 80
分隔： 20 , 10 花费 30  总 110
最优解

贪心思路

每次分隔尽量平均。

如何尽量平均？使用小根堆

public static int separation(int[] arr, int length) {
        int sum = 0;
        if (arr == null) {
            return 0;
        }
        Queue<Integer> queue = new PriorityQueue<>();
        for (int num : arr) {
            queue.add(num);
        }
        while (queue.size() > 1) {
            int cur = queue.poll() + queue.poll();
            sum += cur;
            queue.add(cur);
        }
        return sum;
    }

字符串拼接字典序最小问题

给定字符数组 [‘sdfsd’,‘wef’,‘sew’,‘a’] ，请给出该数组字典序拼接最小的结果

不想写了，说思路吧，贪心最重要的其实就是思路，思路有了解法很简单，基本上排序 或者 用堆 可以解决大部分问题

贪心解法是进行排序，排序比较是根据 如果 o1 拼接 o2 > o2 拼接 o1 则 o1 放到前面

安排会议问题 ，给道 leetcode 的例题吧

1353.最多可以参加的会议数目

在所有开始时间相同的会议中，尽量选择结束时间最小的会议，因为结束时间更大的会议在后续的日程中可选择天数更多

比如在会议：[[1,1],[1,2],[1,3]] 这三个会议中，如果在第 1 天，应该尽量选择 [1,1] 这个会议，因为后面的两个会议，分别可以在第 2 天和第 3 天选择，选择的范围更广

只有这样选择，才可以得到能参加更多的会议

所以，这里我们需要能快速的选择结束时间最小的会议，而且这个最小的结束时间是动态变化的，因为参加了一个会议，就应该排除这个会议

要高效的维护动态数据的最小值可以使用小根堆。