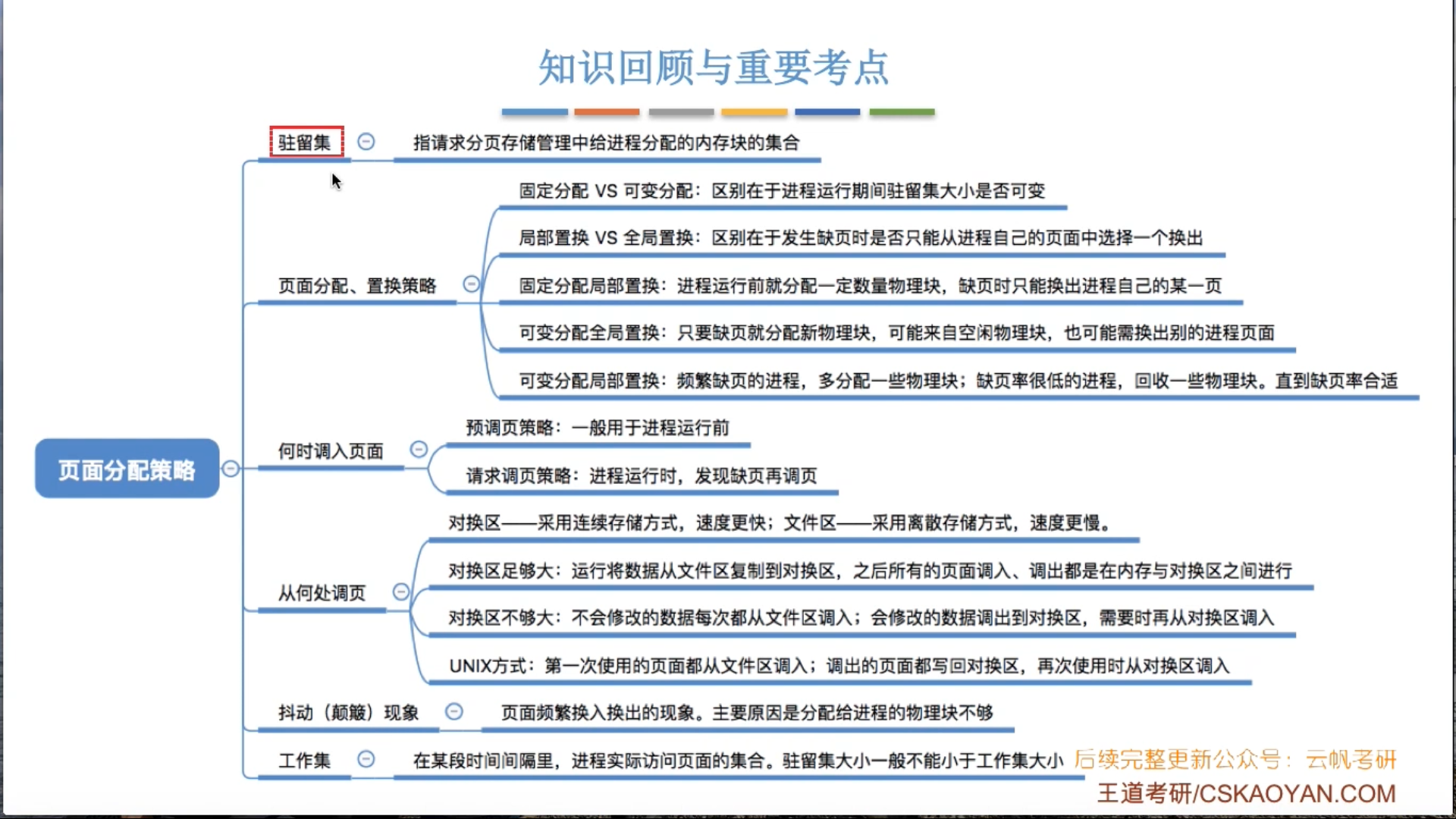
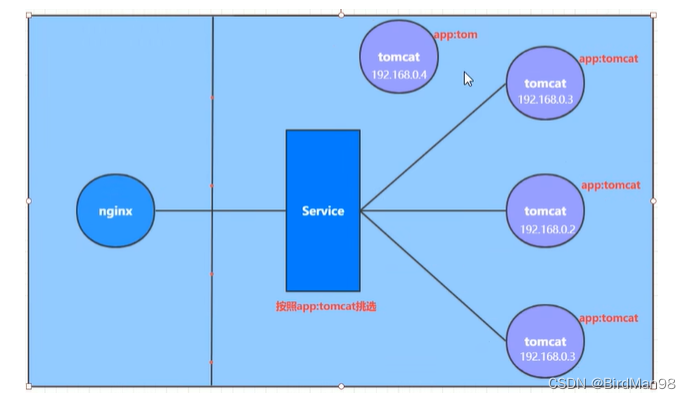
程序=数据结构+算法

数据结构是可以存储和组织数据的命名位置。

算法是用于解决特定问题的一组步骤。

数据结构是指：一种数据组织、管理和存储的格式，它可以帮助我们实现对数据高效的访问和修改。

数据结构 = 数据元素 + 元素之间的结构。

如果说数据结构是造大楼的骨架，算法就是具体的造楼流程。流程不同，效率资源不同。我会两者结合简单探讨下他们的特点和应用。

常见的数据结构可分为：线性结构、树形结构 和 图状结构。

常见的算法有：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法等。

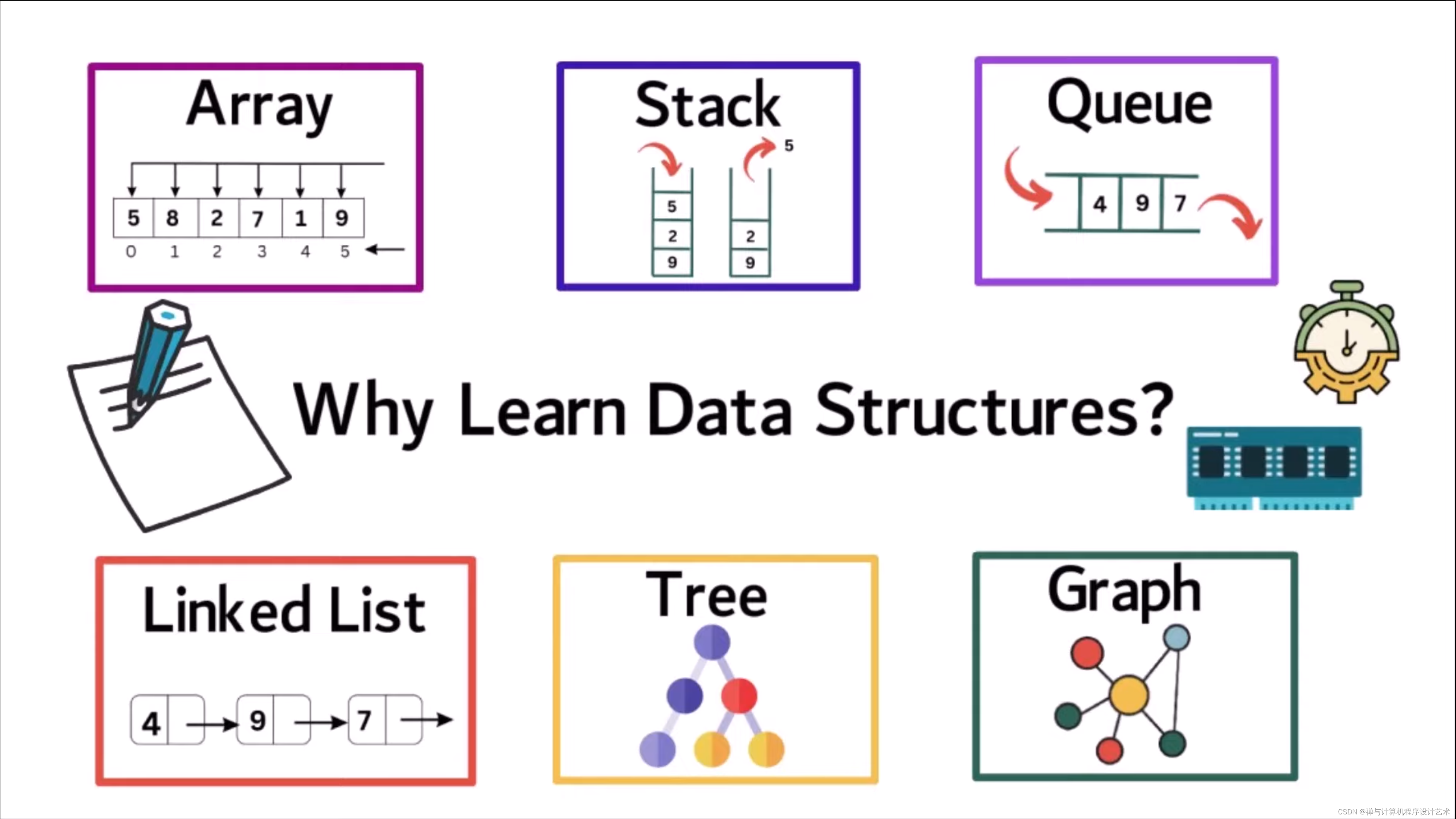
我们可以通过学习数据结构和算法来编写高效和优化的计算机程序。 一旦了解了不同的数据结构和算法，就可以决定在不同的情况下使用哪种数据结构和算法。

了解数据结构和算法将使您能够编写运行速度更快且使用更少存储空间的代码。 百度/腾讯/阿里/字节/微软/谷歌/ Facebook 等公司的求职面试中经常会问到数据结构和算法问题。

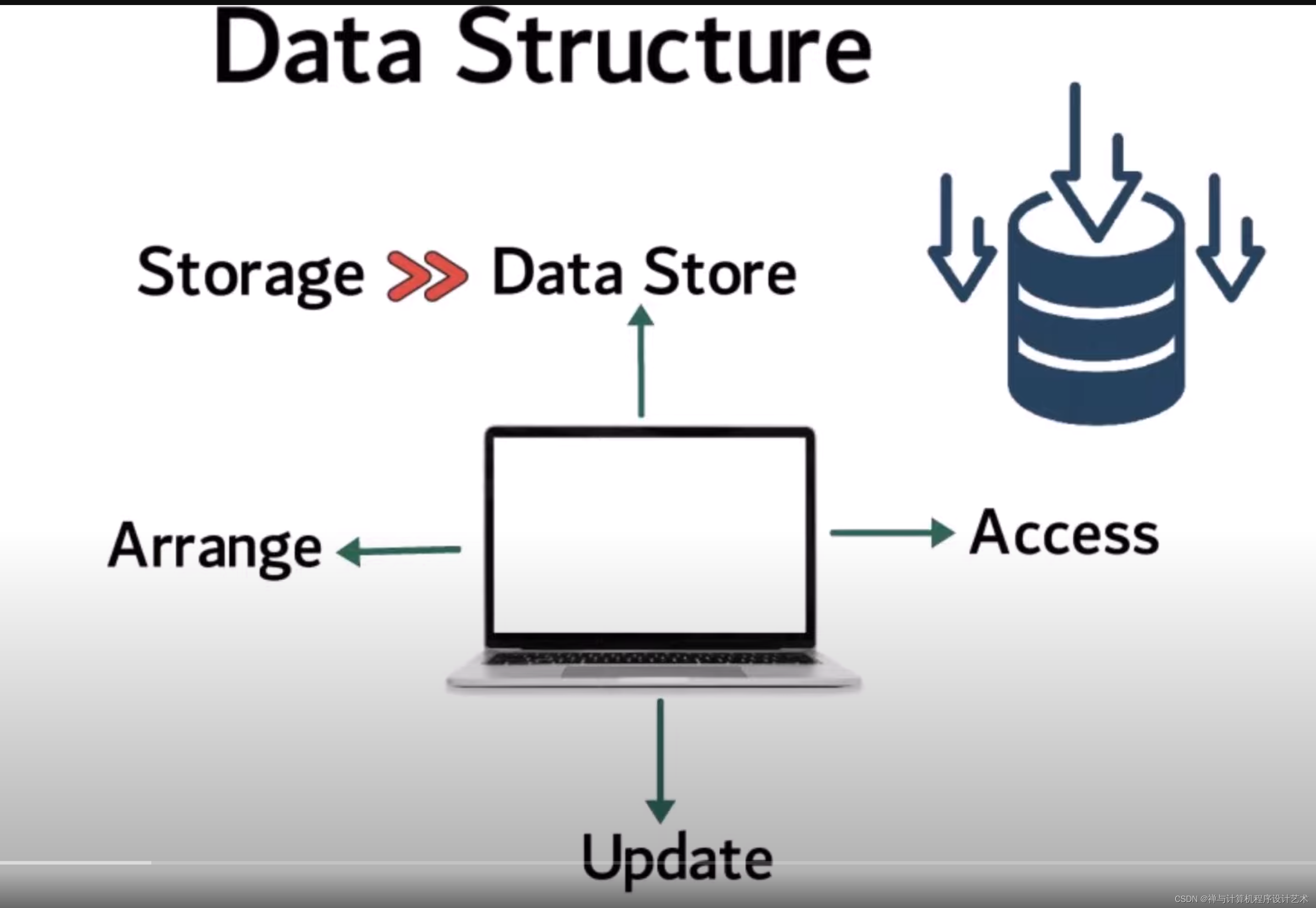
数据的组织和存储

数据怎么组织，组织的逻辑是什么——这就是数据结构。

具体到物理机器磁盘还是内存中的存储——这就是数据的存储。

数据存储的工作原理是什么？

物理数据存储设备是数据存储背后的底层技术。您可以以文件、表格或区块等特定格式从设备读取信息以及向设备写入信息。该设备可以是本地设备、远程设备或在云设备。大型数据存储通常分布在不同地理位置的多个物理设备上。软件系统和服务抽象了数据存储的基础操作。

下面是一些物理设备示例。不同类型的数据存储设备提供不同程度的安全性和冗余。

闪存和 SSD 驱动器

固态硬盘（SSD）是一种半导体技术，可以在闪存芯片中写入和读取数据。在成为普通硬盘（HDD）的替代品之前，闪存技术已可商用于笔式驱动器。与 HDD 相比，物理 SSD 没有移动部件，这意味着其性能更佳且使用寿命更长。

混合存储阵列

混合存储阵列是一种物理存储设置，由 SSD 和 HDD 组成。虽然 SSD 提供低延迟操作，但其单位存储成本比 HDD 高得多。因此，组织使用混合存储阵列来平衡性能、容量和成本。

RAID

RAID 代表独立磁盘的冗余阵列。这是一种将相同数据保存在 SSD 上多个位置的技术。

有哪些不同的数据存储格式？

数据存储旨在处理和组织不同格式的数据。

文件存储

文件存储以自上而下的层次结构将存储的信息整理到文件和文件夹中。计算机使用文件存储让用户可以轻松地存储、搜索和检索信息。您可以使用文件存储系统来存储和组织几乎任何类型的数据。虽然文件存储易于使用，但由于其紧密连接的架构，很难横向扩展。

数据块存储

数据块存储将数据分成多个大小均匀的片段，这些片段称为数据块。数据块存储系统将不同的数据块存储在不同的物理设备上。当用户请求特定数据时，系统会检索并重新组合这些片段。该系统使用映射系统根据基块元数据定位请求的数据。元数据是帮助用户或应用程序在存储中查找特定信息的附加信息。

对象存储

对象存储将非结构化数据存储在可扩展、独立的存储库中，该存储库可以托管在不同的服务器上。属于某个对象的每个数据块都在其元数据中进行了描述。例如，对象可以存储社交媒体内容、视频、电子邮件和音频文件。应用程序通过使用视频分辨率、持续时间和位置等特定的元数据属性在对象存储中搜索信息。

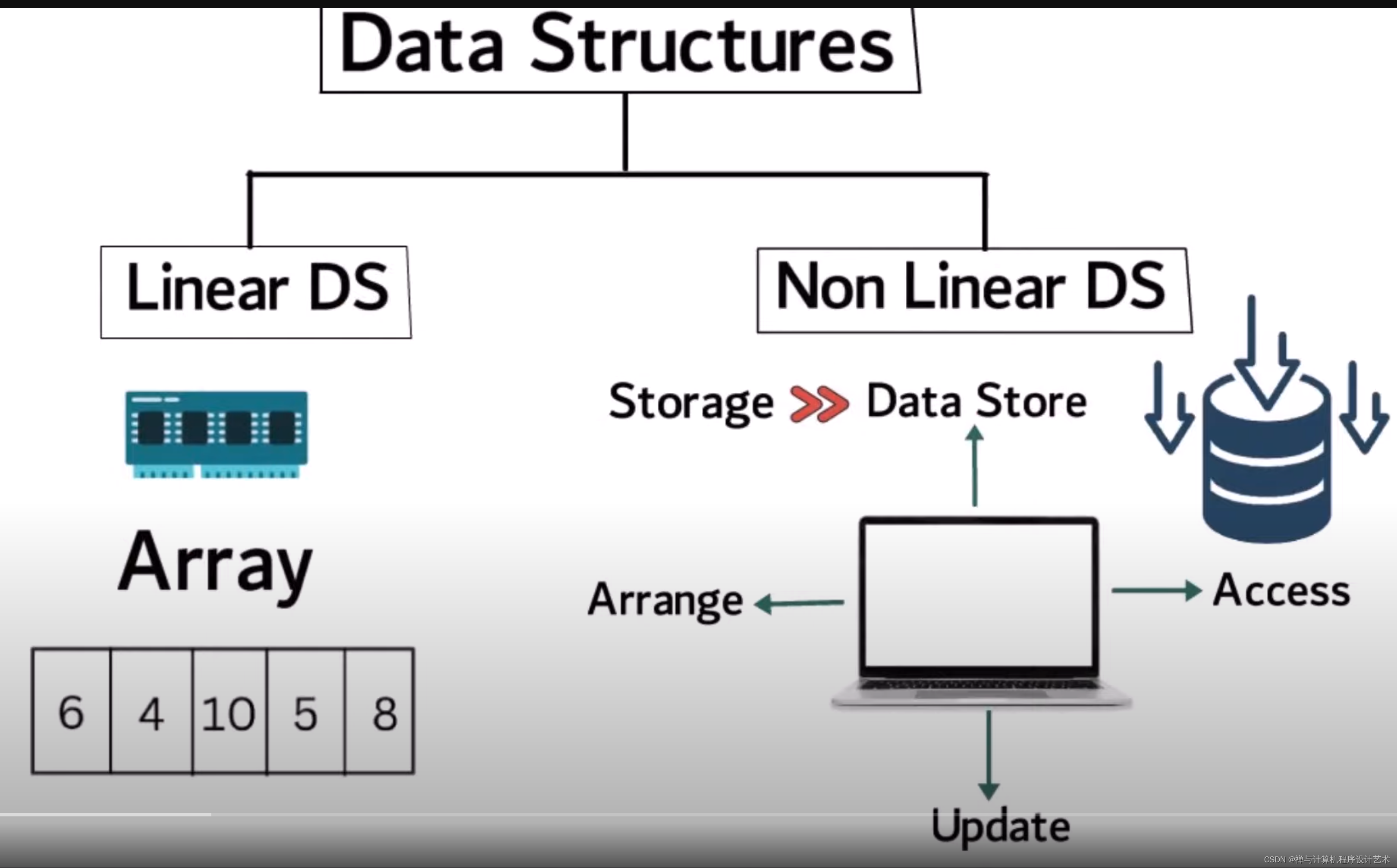
 线性与非线性数据结构

线性数据结构是指数据元素之间存在一对一的线性关系，比如数组、链表、栈和队列等。非线性数据结构是指数据元素之间存在多对多的关系，比如二叉树、图、哈希表等。

 线性数据结构

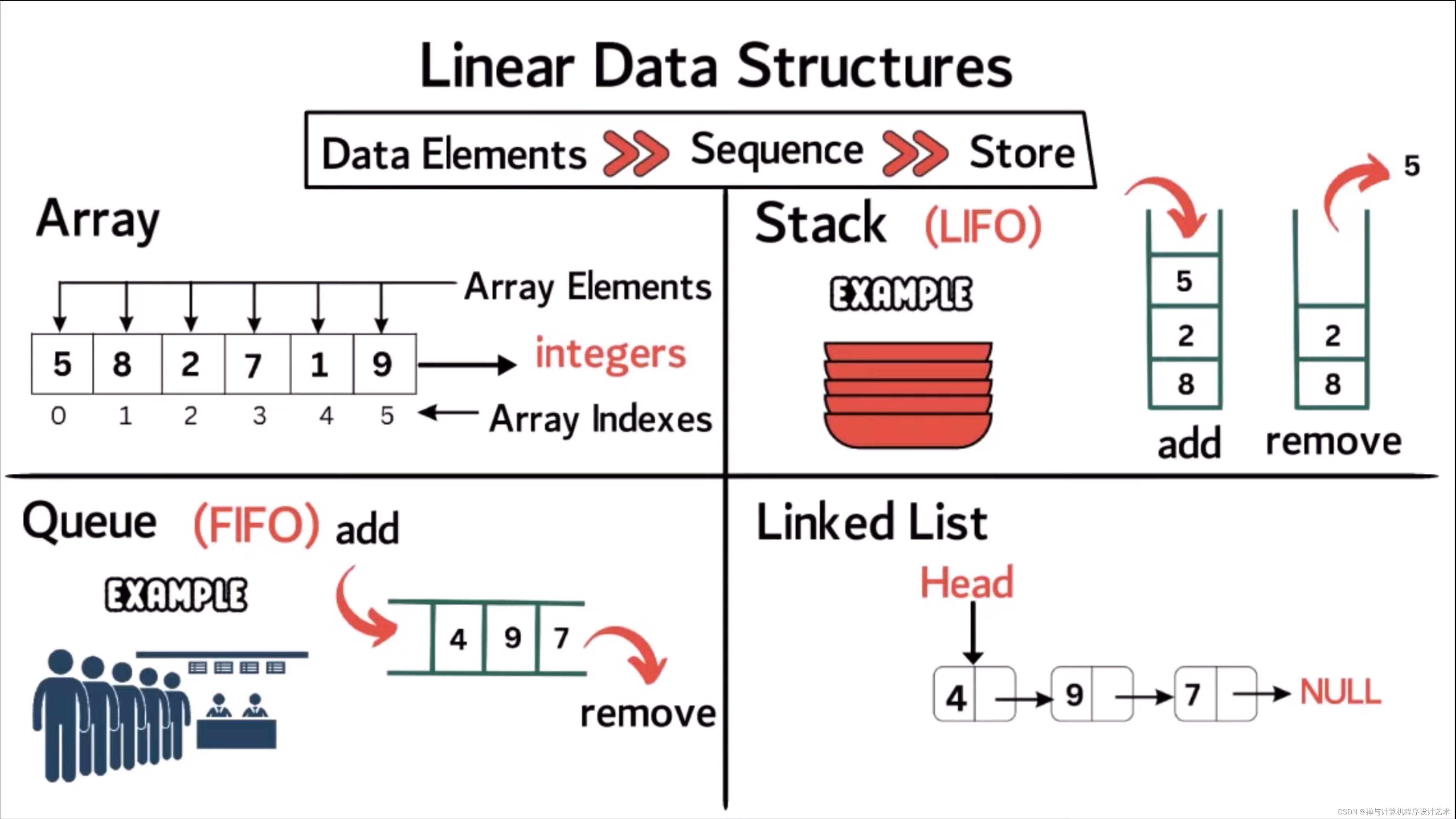
非线性数据结构

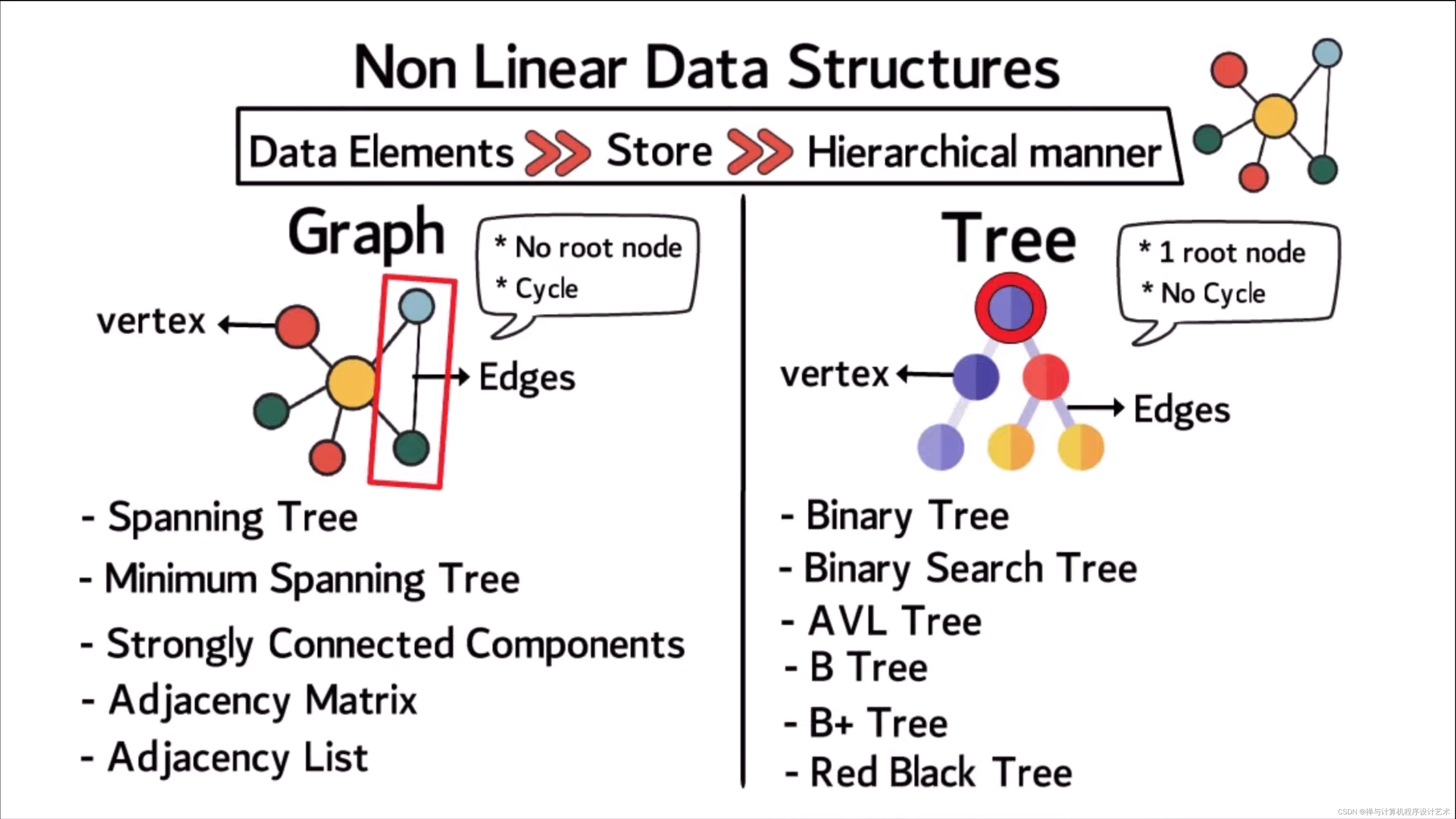
 算法

线性结构

线性结构：是指数据排成像一条线一样的结构。每个元素结点最多对应一个前驱结点和一个后继结点。如数组, 链表，栈 ，队列等。

数组

数组是是由相同类型的元素（element）的集合所组成的数据结构，分配一块连续的内存来存储。利用元素的下标位置可以计算出该元素对应的存储地址。

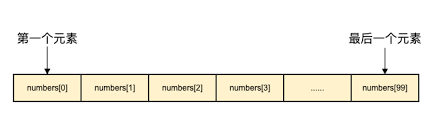
优点： 分配基于连续内存，是一种天生的索引结构，查询修改元素的效率O(1)。同时可以借助 CPU 的缓存机制，预读数组中的数据，所以访问效率更高。

缺点： 数组的索引优点也是它的缺点，因为它的索引是基于一块连续内存元素存储的位置下标决定的，增删arr[i]时间复杂度O(n)，需要整体移动数组arr[i-n-1]的位置。此外，分配大数组会占用较大的内存。

可通过以下方式避免元素拷贝和占用大的开销：

1.懒删除：删除时只标记元素被删除，并不真正的执行删除。当数组整体内存不够用时，再执行真正的删除。 2.分块思想：将一大块内存分为n个小块，以 小块 为单位进行数组内存的拷贝。如Mysql的InnoDB引擎中每个Buffer Pool实例由若干个chunk组成，实际内存申请操作以chunk为单位。 3.缩容：曾经面试阿里时，就让设计了一个缩容版的HashMap。浪费可耻，节约光荣。 4.链表。

链表

链表的存在就是为了解决数组的增删复杂耗时，内存占用较大的问题。它并不需要一块连续的内存空间，它通过 指针 将一组零散的内存块串联起来。根据指针的不同，有单链表，双向链表，循环链表之分。

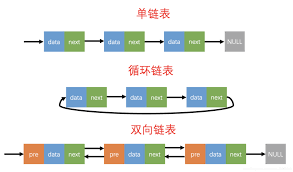
优点： 增删arr[i]时间复杂度O(1)，使用链表本身没有大小的限制，天然地支持动态扩容。

缺点： 没有“索引”，查询时间复杂度O(n)。需要维护指针，更占内存。同时内存不连续，容易造成内存碎片。

可以看出：数组和链表是相互补充的一对数据结构。那怎么弥补链表的不足呢？

内存这块是不好解决，这是由 指针 决定的。关于索引，没索引就帮它建索引好了：

1.结合hash表，记录链表每个结点的位置。 2.链表长度拉的过长时，考虑跳表，红黑树这类数据结构。（别慌，后面会讲～）

应用场景： 数组和链表的运用很广泛，他们是构成 数据结构的基础。如栈，队列，集合等等。

栈

栈是一种受限制的线性数据结构。元素只可以在栈顶被访问。 符合先进后出的First-In-Last-Out的访问方式。

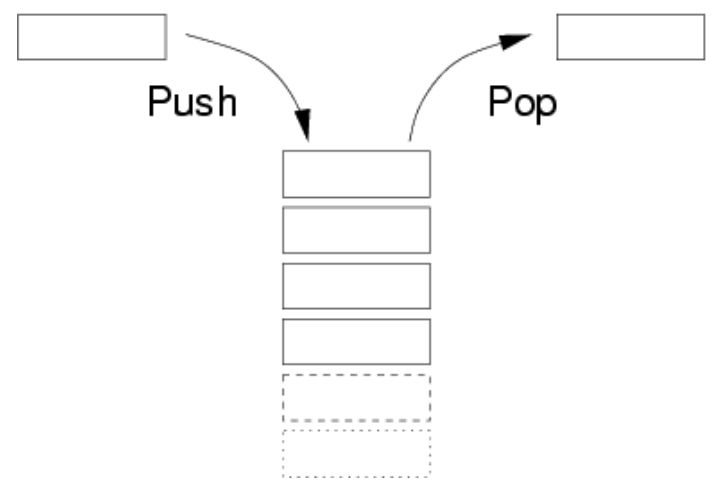
用数组实现的叫顺序栈，用链表实现的叫链式栈。可能有人会有疑问：我用数组链表在头尾两端可伸可缩，为毛要用只能在头部操作的栈结构呢？ 这种FILO的结构当然是只适用于FILO的场景。如果我们将数组/链表这种结构封装为栈，就可以只使用其pop/push的API，屏蔽掉实现细节。

应用场景： 1.编辑器的redo/undo操作。 2.浏览器的前进/后退操作。 3.编译器的括号匹配校验 4.数学计算中的表达式求值 5.函数调用 6.递归 7.字符串反转...

队列

队列也是一种受限制的线性数据结构。 符合先进先出的First-In-First-Out 的访问方式。同样，用数组实现的队列叫作顺序队列，用链表实现的队列叫作链式队列。

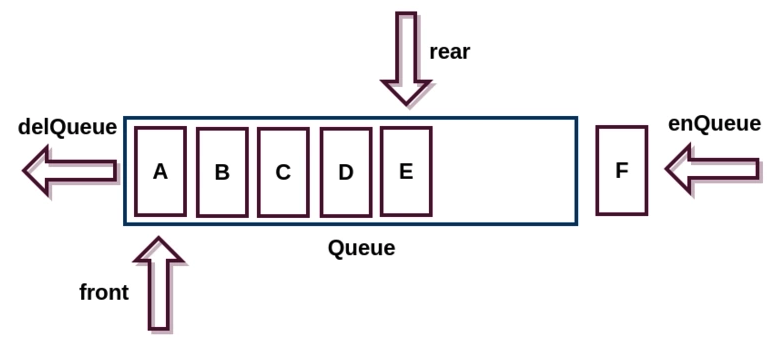
根据头尾指针和操作的不同，队列又可分为双端队列，循环队列，阻塞队列，并发队列。

• 双端队列：头尾均可以进行插入，删除，访问元素，更为实用。不存在FIFO这种限制。

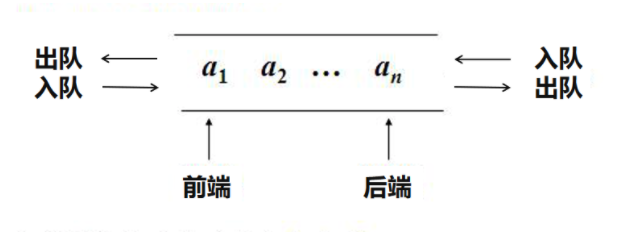
• 循环队列：把队列的头尾相连接并且使用顺序存储结构进行数据存储的队列。

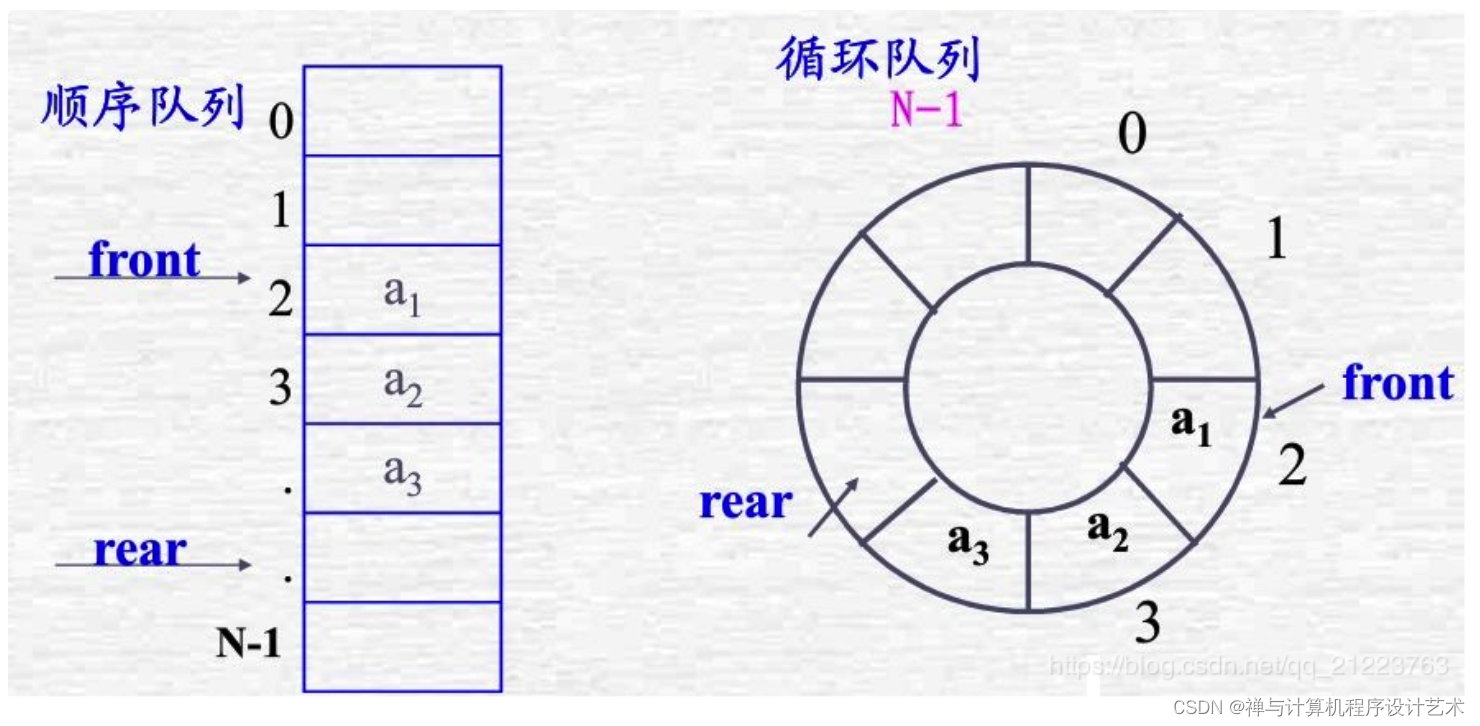
存在并发的场景下，队列存取元素的临界区为 队列空时的取操作 和 队列满时的存操作。保证并发下的队列存取安全为阻塞队列 和 并发队列。两者的区别在于 同步资源的粒度不同。

• 阻塞队列：通过 互斥锁 保证enqueue、dequeue的安全，锁粒度较大。如Java JUC包中的阻塞队列。
• 并发队列：基于数组的循环队列，利用 CAS 原子操作保证enqueue、dequeue的安全。 其实就是通过：多次volatile读 + CAS操作 这种乐观思想 修改头尾指针的位置，保证enqueue、dequeue的安全。CAS的同步代价小较小，所以称为：无锁并发队列。如Disruptor框架中Ring Buffer就运用了这点。

PS: 很多框架对线程池的需求都替换成了Disruptor来实现，如Log4j2、Canal等。

应用场景： 队列的作用其实就是现实中的排队。当资源不足时，通过“队列” 这种结构来实现排队的效果。用于： 1.任务调度存在的地方：CPU/磁盘/线程池/任务调度框架... 2.两个进程中数据的传递：如pipe/file IO/IO Buffer... 3.生产者消费者场景中.. 4.LRU

递归实现

递归 是一种算法求解的编码实现。应用于如深度优先搜索、前中后序二叉树遍历（挖坑后面讲～）等。因为接下来的排序算法如：归并/快排 可通过递归来实现，所以我们先看一下书写递归的步骤。熟悉了递归的思想，它其实是一种书写简单的编码方式。

只要问题满足以下三点，均可使用递归来进行求解：

1.一个问题的解可以分解为几个子问题的解 2.问题和子问题之间，除了数据规模不同，求解思路完全一样 3.存在递归终止条件

写递归代码的关键在于：找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再敲定终止条件，最后将递推公式和终止条件翻译成代码。

因为人并不擅长处理这种程序，所以在写递归代码的时候，我们可以自动屏蔽掉递归的执行过程。我们只需要告诉程序：递推公式 和 终止条件 是什么，事情就会便Easy~

使用时的注意项：

1.stackoverflow: 实际函数调用层次太深，就会有系统栈或者虚拟机栈空间溢出的风险。

2.子问题的重复计算： 前面文章我有讲 动态规划通过避免子问题的重复计算能够降低时间复杂度。一种方式就是通过 递归 + 备忘录（子问题的解保存起来）来解决。

排序算法

233酱学习的第一个算法就是冒泡排序算法，我想不少码农都经历过被 “几大排序算法” 支配的恐惧。

排序是我们在项目工程中经常遇到的一个场景，如TopK，中位数问题等。有序 和 无序 的数据集合之间的差别在于 前者 “逆序对” 为0.

小贴士： 如果i < j，且a[i] > a[j], 就称为一个逆序对，如 1，7，3，5 中的 <7，5> 反之则为有序对，如<1,3>

不同的排序算法消灭逆序对的方式不一样，体现在时空复杂度，排序方式，稳定性，适用场景等方面不同。

我先放一张网上排序算法的图：

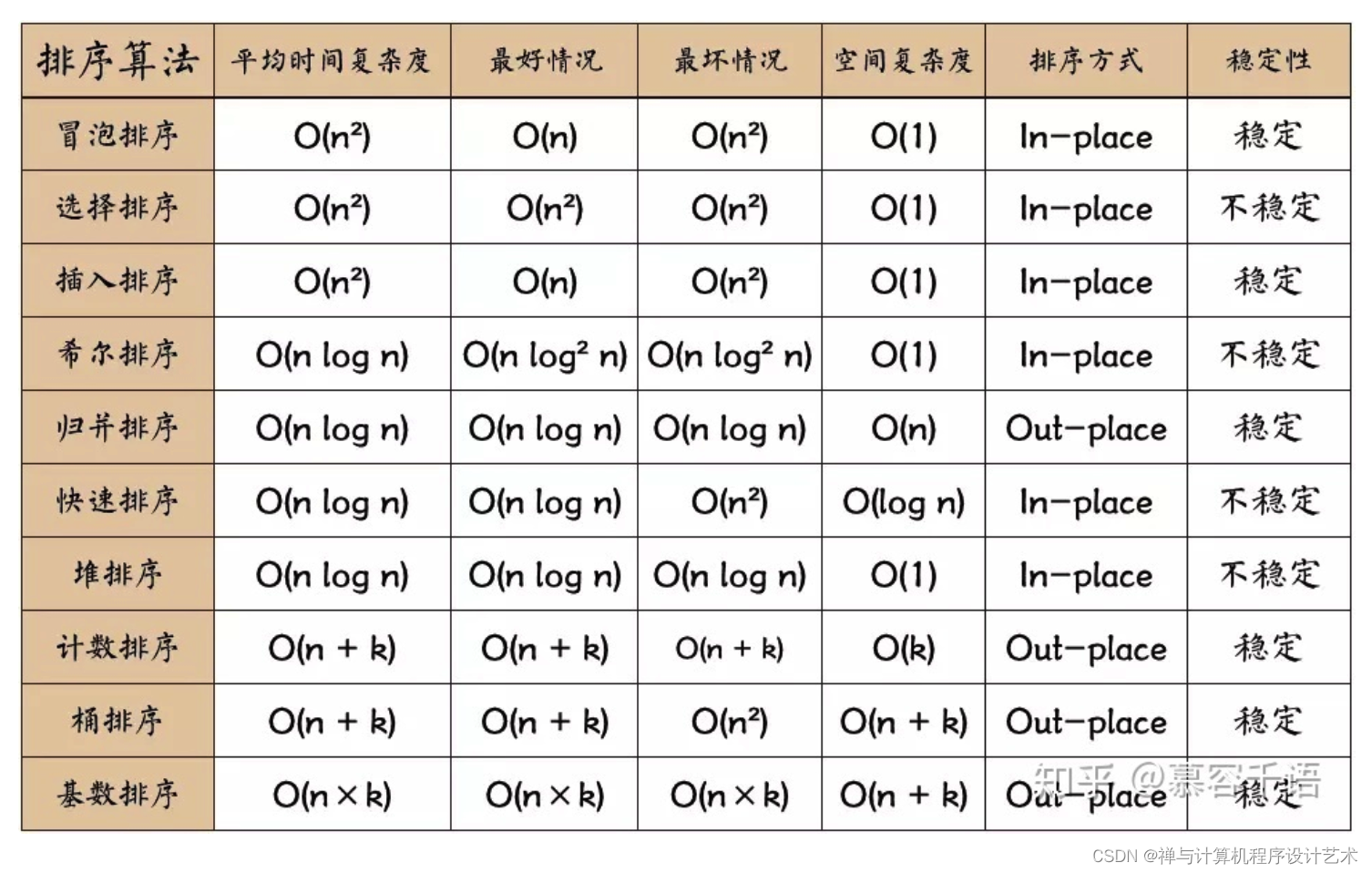
选择排序算法时，我们应该考虑算法的执行效率，内存消耗，稳定性等这些因素。

PS：以下内容主要引用极客时间王争大佬的《数据结构和算法之美》课程，233能力有限，默默给大佬打广告&点赞。

如何分析排序算法的执行效率

1. 最好情况、最坏情况、平均情况时间复杂度

对于要排序的原始数据，数据的有序度不同，对排序的执行效率是有影响的。比如接近有序的待排序数据 插入排序的时间复杂度接近O(n)。我们需要了解排序算法在不同数据下的性能表现。

2.时间复杂度的系数、常数 、低阶

在对小规模的数据排序时，如10个，100个，1000个。需要把系数、常数、低阶也考虑进来，才能选择合适的排序算法。

3.比较次数和交换（或移动）次数

基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，如果我们在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

排序算法的内存消耗

上图中有一列排序方式：原地排序（In-place） 和 外部排序(Out-place)。前者是指空间复杂度为O(1)的排序算法，不需要在外部开辟内存空间。后者需要额外开辟空间来存储中间状态。前者的好处在于可以借助 CPU 的缓存机制，访问效率更高。这是一个重要的考量因素。

小贴士：快排的空间复杂度为是因为它的实现是递归调用的， 每次函数调用中只使用了常数的空间，因此空间复杂度等于递归深度O(logn)。

排序算法的稳定性

稳定性是指：待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序是不变的。

为啥要考虑排序算法的稳定性呢？ 这是因为实际场景中的待排序的对象 排序维度可能是多个。比如我们对订单先按照金额排序，再按照下单时间排序。实现简单的思路为：先给订单按照 下单时间排序，再按照金额排序。 稳定性的排序算法能够保证 金额相同的两个对象，在排序之后的下单顺序不变。

下面主要从数据规模上讨论这些排序算法的应用。

小规模数据排序

在小规模数据下，冒泡排序/选择排序/插入排序实现较为简单，排除不稳定的选择排序，插入排序（可类比打扑克抓牌时的排序思想）比冒泡排序（最大元素依次往后冒）好在交换次数少，小规模下排序效率更高。

此外当待排序序列的有序度比较高时，插入排序也好过归并/快排这类O(nlogn)的效率。所以在小规模数据场景下，适合用插入排序。

大规模内存级数据排序

大规模数据排序适合考虑O(nlogn)级别的排序算法，这里讨论 归并排序 和 快速排序。

归并排序的思想是 分治 思想。将整个无序序列的排序 划分为 无序小序列的排序问题。子序列有序了，再合并起来有序的子序列，整体就排好序了。 归并排序是外部排序。每次合并操作都需要申请额外的内存空间，在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。

快速排序利用的也是 分治 思想。局部有序 最终 全局有序。它使用一个分区点数据(pivort)将元素分为< pivort,=pivort,>pivort三个部分。然后在< pivort 和 >pivort这两部分继续递归处理，最终排序完成。

如果 快排合理的选择pivort，多路指针参与分区可以避免时间复杂度的恶化。而且快排是原地排序，相比归并排序是外部排序，空间复杂度较高O(n)。快排的应用更为广泛。

Java中Arrays.sort是混合排序，实现策略分为两种：

Case1. 存储的数据类型是基本数据类型

使用的是快排，在数据量很小的时候，使用的插入排序；

Case2. 存储的数据类型是Object

使用的是归并排序，在数据量很小的时候，使用的也是插入排序

大规模外部数据排序

当数据规模很大时，我们并不能把所有数据都加载到内存。这时候可以考虑时间复杂度是 O(n) 的外部排序算法：桶排序、计数排序、基数排序。外部排序是指数据存储在外部磁盘中。

这里时间复杂度之所以低是因为：这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。

桶排序是按照某种属性将元素分配到全局有序的子桶内，再在子桶内做局部排序。当子桶个数划分的足够大时，时间复杂度就接近O(n) 。

计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

基数排序是根据每一位来排序，基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到 O(n) 了。