神经网络的生物学原理

在最开始，人们想要构建一个能够模拟生物大脑来进行学习和思考的算法程序，于是从生物学的结构出发，创造了神经网络算法。
如果你对高中生物比较熟悉，那么应该能够更好地理解下面的知识。
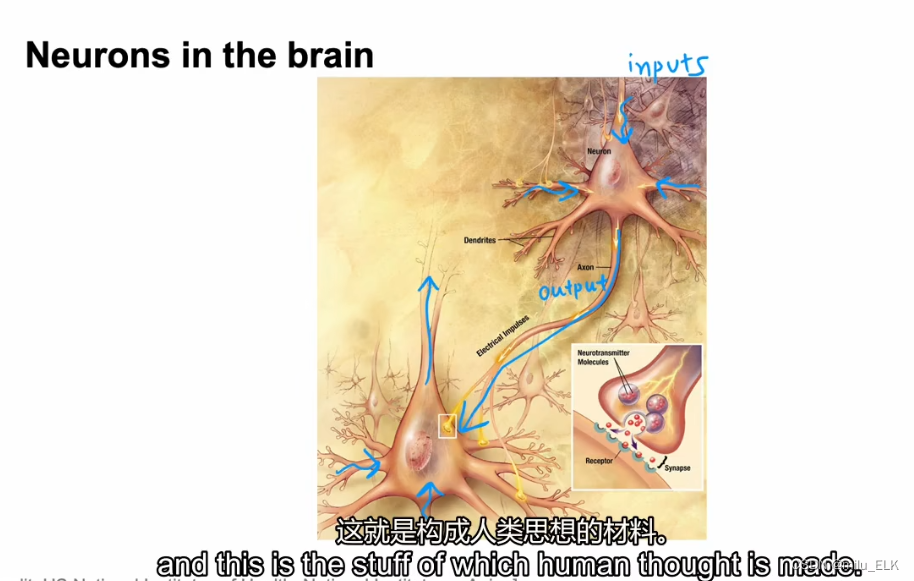
在这里插入图片描述

在人类的大脑中布满了神经元细胞，它是神经系统最基本的结构和功能单位，我们的思维就起源于神经元。在人体中信号是以电脉冲的形式传递的，神经元之间的信号传递我们称之为"兴奋"，兴奋的传递过程就是通过外部刺激产生电信号，并在神经元的突触之间传输，最终实现思考等神经活动。
如果将其类比为程序，相当于对神经元A输入input，由神经元A输出给神经元B，再由神经元B输出给神经元C…最后输出需要的结果。
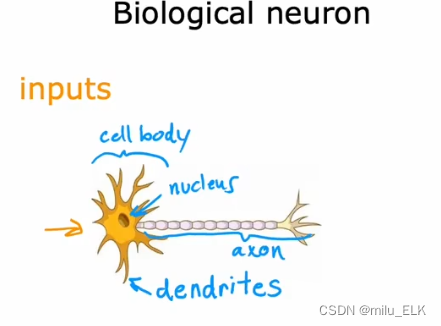
在这里插入图片描述
这是单个神经元的结构，上方被称为胞体，其散发出的触手状结构称为树突，下方长条状结构称为轴突，尾部被称为轴突末梢。神经元之间的连接就是头尾相连的状态。
如果将这种结构简化为数学模型，那么就如右图所示，我们将原图中的一个神经元看作一个单元，给予第一个单元input值，经过第一个单元的计算后的output值再输入到下一个单元中，这就是神经网络的原理。
神经网络算法之所以在近几年异军突起，得益于硬件的发展实现了越来越快的计算机处理，以及大数据。
（我们只是借用生物学的动机来模拟思考过程，生物学发展十分迅速，不要拘泥于生物学的具体实际）

神经网络的算法结构

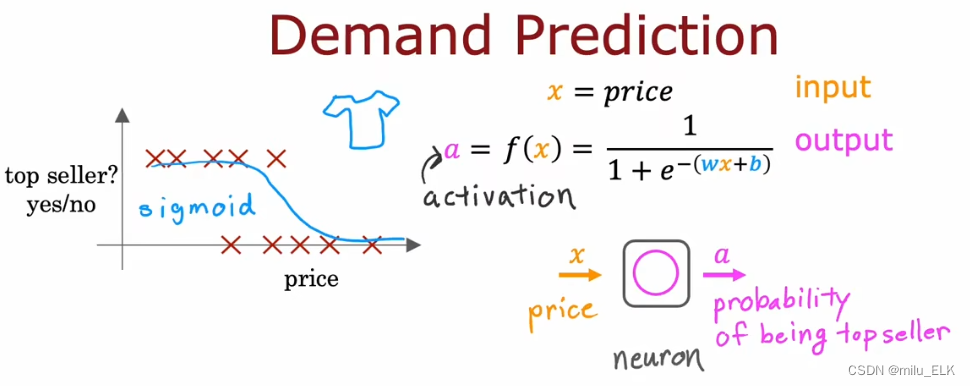在这里插入图片描述假设你开了一家服装店，给出一个特征：比如服装的价格，你想预测什么样的服装是最畅销的。把它看作是一个分类问题，那么我们应该用逻辑回归来解决，如上图所示。
我们知道 $f (x)$ 代表了假设函数，在分类问题中用到的是logistic函数，但是在神经网络中我们给它取一个新的定义：activation(激活)，简称a，这是借用了神经学中的术语，指的是上游神经元向下游神经元发射的兴奋。
如果我们将函数 $f (x)$ 简单地看成一个单元，一个微型计算机或者一个电路中的元件，如右下所示，我们输入x后得到了结果a，在本题中a即逻辑函数的预测值。这就好比单个神经元在整个神经网络中实现的工作。
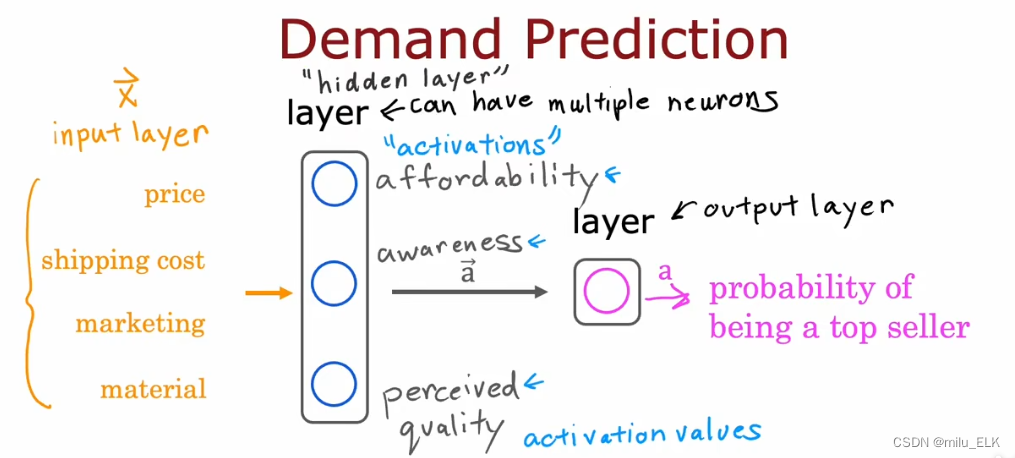
在这里插入图片描述

现在我们多添加几个输入特征，并且根据这些特征得到三个神经元的结果来预测最终的畅销可能性。如图所示：
第一个神经元通过特征price和shipping cost来预测成本affordability
第二个神经元通过特征marketing来预测知名度awareness
第三个神经元通过特征price和material来预测质量quality
成本、知名度、质量，这三个要素对于最终畅销可能性的预测都是必要的，最后我们将这三个要素输入到最后的神经元，其输出结果就是最终的畅销可能性的预测值。
如果我们将中间蓝色的三个神经元分为一组，我们称其为“一层”，右边粉色的单个神经元我们也称为一层（相信计算机专业的对于层这个概念一定很熟悉了），同样的最左边的输入特征也可以归为一层。我们将最初用于输入的那一层称为输入层，最后一层被称为输出层。
对于中间层的输出结果，我们称其为activation(激活)，我们将中间层称为隐藏层(hidden layer)
尽管我们可以用给出的特征来直接进行预测，但是显然用隐藏层给出的结果来预测要比直接用特征预测更加准确。
你可能想起了我们之前在讲特征工程的适合，将房子的长和宽两个特征合并为面积，区别在于我们在特征工程中需要手动来构造更复杂的特征，然而在神经网络中是不需要的，它可以自己学习特征。当你使用神经网络的时候，你不需要特别指出特征，它可以自己计算在隐藏层中所要用的特征。
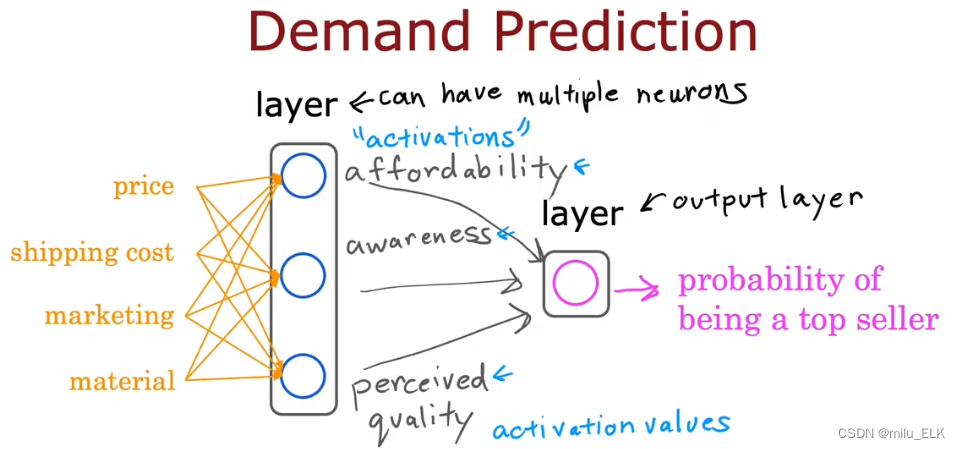
在这里插入图片描述
由于我们的输入值通常是整个特征向量，因此所有的特征都要经过隐藏层的计算，因此隐藏层可以自动地选择需要的特征。

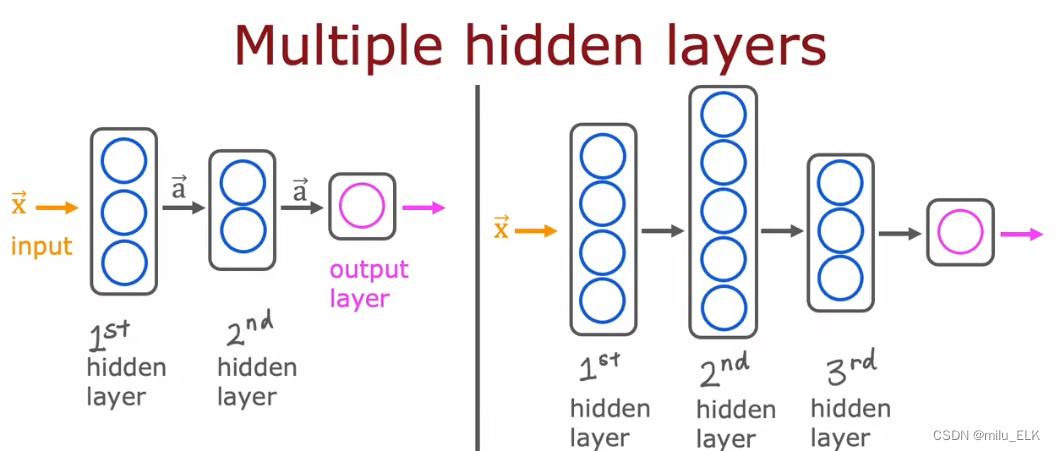
对于不同的神经网络，我们可以设置多个隐藏层，每个隐藏层设置任意多个神经元。正常选择隐藏层和神经元的数量可以有效提高算法效率。
由于程序的表现是“输入——>计算——>输出”，其中隐藏层位于计算部分，由于整个程序就像是一个黑盒，因此我们看不到中间层的计算方法，所以将中间层称为隐藏层。

案例——图像感知

在这里插入图片描述
图像是怎么进行识别的？首先假设给出一个1000p（像素）x1000p。以亮度值为特征，每一个像素都有对应的强度值，因此我们可以把整张图像的亮度值看成一个1000x1000的矩阵，如果要作为向量进行输入，那么我们将其按行展开得到输入向量x
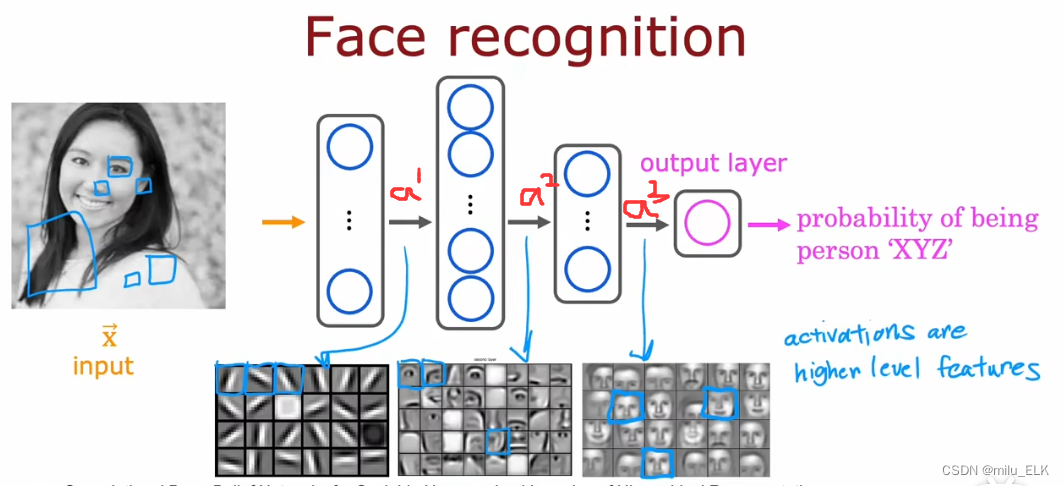
在这里插入图片描述

我们最终想要识别出此人是谁的概率。在人像识别的过程中需要经历数个隐藏层的计算，例如以上图为例经过了三个隐藏层，第一层中，第一个神经元可能想要寻找到拥有竖直边缘的第一个像素，第二个神经元想要找到一条像这样有方向的线或者有方向的边，第三个神经元可能想在这个方向上寻找一条边，因此在第一层中，神经元试图找到图中的一些非常短的线段或者边缘，最终输出的激活值 $a^{[1]}$ 就是第一层下方的一些包含了线段的集合。

第一层的那些线段，就是器官的边缘部分，它们能够帮助我们构建出器官的形状。在第二层中，我们将上一层的 $a^{[1]}$ 作为输入，一些神经元可能会将部分小短线、小短边段组合在一起，来检查是否找到了一些器官的位置，比如在 $a^{[2]}$ 的输出集合中，第一个神经元可能在寻找左眼的位置，第二个神经元在寻找鼻子的底部的位置，第三个在寻找鼻梁的位置…

那么通过第二层我们找到了器官的整体形状和位置，有了五官之后我们就能构建出一个模糊的人脸。在第三层中，神经元正在聚合面部的不同部分，试图建立粗粒度更大的面部轮廓，并在最终检验五官与不同面部轮廓的适配度，最终形成 $a^{[3]}$ 来帮助输出层判别人像身份的概率。

更神奇的是，在整个神经网络的工作过程中，不需要人来制定神经元的工作，没有人规定第一层要找到线段，第二层找器官，第三层找脸型…神经网络能自己从数据中找出这些东西。此外，随着特征复合程度变高，输入窗口也会变得越来越大，第一层的窗口可能是小号的，第二层变为了中号，第三层变成大号窗口，上图中可视化的神经元输出集合，每层的格子都代表了不同大小的窗口。

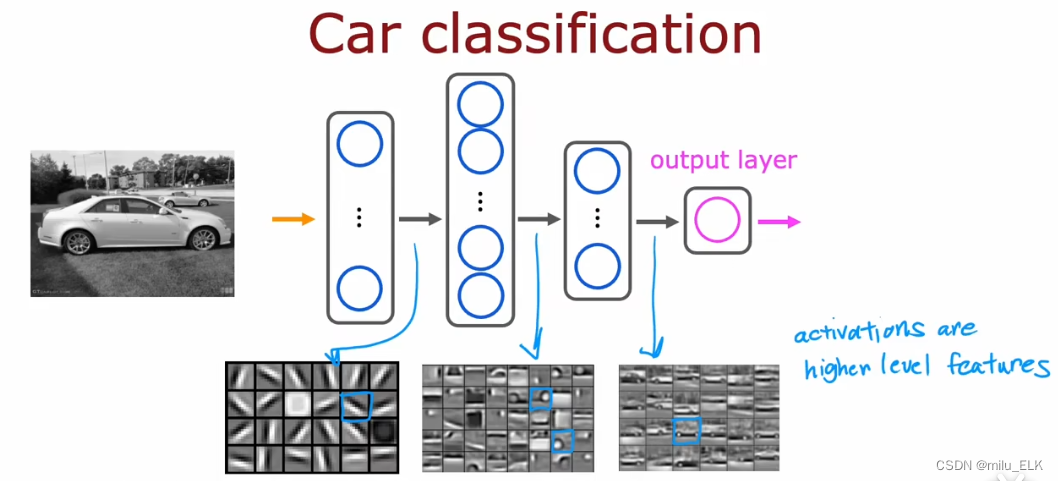
在这里插入图片描述
如果我们在同一个神经网络中，将人像的输入换为汽车图像的输入，那么它也会自动寻找边缘线段、汽车结构、整体…对于不同的数据，神经网络会自动学习检测不同的特征，从而完成检测是否存在某个特定事物的工作。

神经网络的前向传播

在这里插入图片描述在神经网络中，由于往往存在上百个神经元甚至上百个层级，因此我们有必要对其中的数值进行标号。
我们把输入层看为第0层，层数依次递增，输入层的输入向量被称为向量 $\vec x$ ,在上图中，第一层有三个神经元，每层神经元都是一个逻辑函数，其中上标 $[1]$ 代表当前的层级，下标 $n$ 代表是当前层级第 $n$ 个神经元，例如第一个神经元中的系数向量 $\vec w^{[1]}_1$ ,第二个神经元中的系数向量就是 $\vec w^{[1]}_2$ ，如果是第二层第三个神经元中的系数向量就标为 $\vec w^{[2]}_3$ …我们可以看到，第一层神经元的计算结果依次是0.3，0.7，0.2，最终可以合并为一个输出向量 $\vec a^{[1]} =\begin{bmatrix} 0.3 \\ 0.7 \\ 0.2 \end{bmatrix}$ ,代表激活向量a是第一层的输出结果，之后它将被输入到第二层。

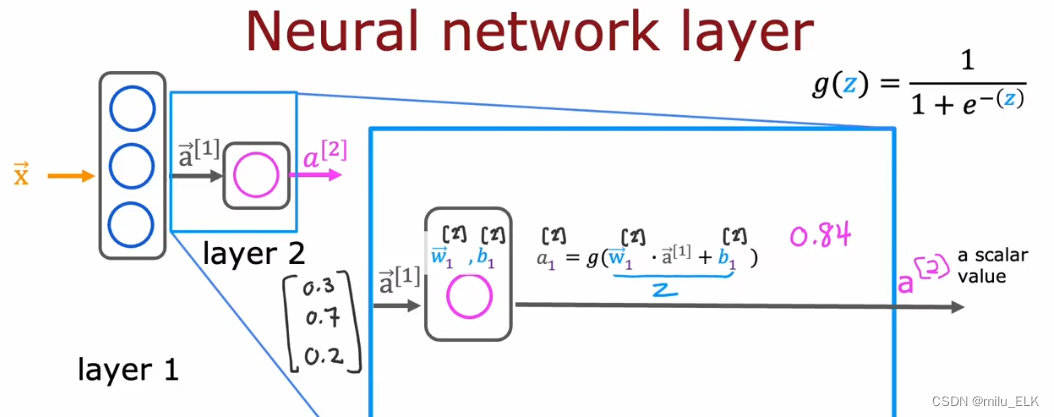
在这里插入图片描述
第二层也是同理，由于第二层是最终的输出层，所以最终得到的第二层的输出结果 $a^{[2]}$ 应当是一个确切的数值。层级之间的作用就是输入一个向量，并通过运算得到另一个向量。输入层也可以视为 $\vec a^{[0]}$ 。

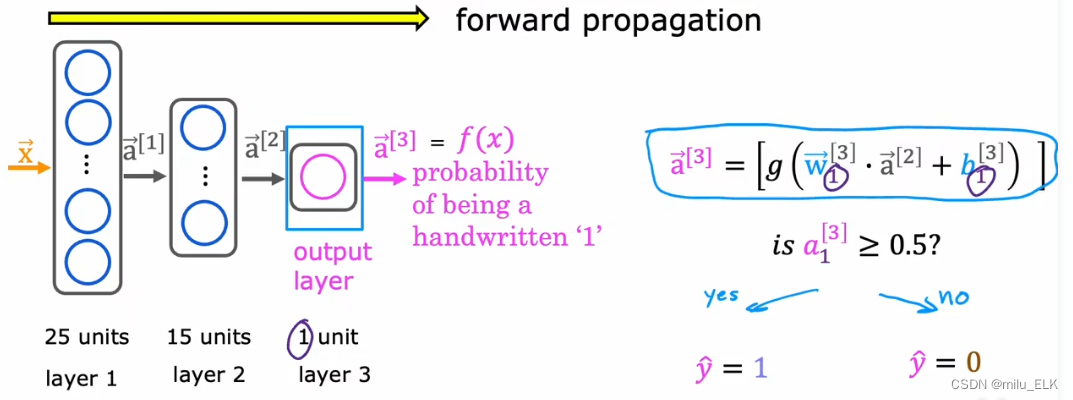
在这里插入图片描述
由 $\vec x$ 到 $\vec a^{[1]}$ 到 $\vec a^{[2]}$ …最终到输出结果 $\vec a^{[n]}$ ，这种从左向右的计算过程，我们称之为神经网络的前向传播，最后的输出结果我们也可以称之为 $f (x)$ ，还记得我们之前的过程中，对于线性回归或者逻辑回归的假设函数的输出结果也称为 $f (x)$ ，我们现在可以用它来表示神经网络的函数。而其也存在一个相反的神经网络，我们称为反向传播，一般用于学习。
一般来讲，神经网络的结构总是随着层级的变大，其隐藏层单元的数量会越来越少。