Conditioning of a problem
该博客是学习《Numerical Linear Algebra with Applications Using MATLAB》的一些总结,仅供学习使用。
通常即使使用一个稳定的算法来解决一个问题,该问题对数据中小的改变或扰动仍然是敏感的。这些扰动可能来自舍入误差(roundoff error),收集实验数据时的小的测量误差,没有被信号过滤的噪音,近似无穷级数时的截断误差等。如果该问题落入此类,则称该问题为ill-conditioned(病态的)。
Def 1: 不管用什么算法来解决一个问题,如果它的数据中的一个小的相对变化会导致它的计算解的一个大的相对误差, 则称这个问题是病态的(ill-conditioned),如果问题数据中的小扰动导致计算解的小相对误差,则称问题是良态的(well-conditioned)。
需要搞清楚两个概念:stability 和 conditioning。
- Stable or unstable 是对于算法而言的;
- Well or ill-conditioned 是指特定的问题而非使用的算法。
显然,将不稳定的算法应用于病态的问题是在自找麻烦。(asking for disaster).
但是,对于求解某个问题而言,一个稳定的算法也会产生差的结果,如果输入数据时病态的。 我们假定 f ( x ) f(x) f(x)表示一个算法, x x x表示数据。 我们可以利用 f ( x ) f(x) f(x)来定义well 和ill-conditioning.
Def 2. 定义 x x x和 x ˉ \bar{x} xˉ分别是初始数据和扰动数据, f ( x ) f(x) f(x)和 f ( x ˉ ) f(\bar{x}) f(xˉ)是对应的解,则有
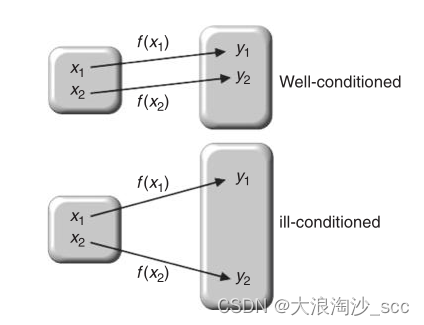
如果 ∣ x − x ˉ ∣ |x-\bar{x}| ∣x−xˉ∣很小, ∣ f ( x ) − f ( x ˉ ) ∣ |f(x)-f(\bar{x})| ∣f(x)−f(xˉ)∣也很小,则该问题关于数据 x x x是well-conditioned.
如果 ∣ x − x ˉ ∣ |x-\bar{x}| ∣x−xˉ∣很小, ∣ f ( x ) − f ( x ˉ ) ∣ |f(x)-f(\bar{x})| ∣f(x)−f(xˉ)∣很大,则该问题关于数据 x x x是ill-conditioned. 如下图*
问题对数据的敏感性可以通过定义条件数(condition number)来测量。 条件数越大,则该问题对数据的改变的敏感性越高。
对于一个特定的数据
x
x
x,假定数据中有很小的误差,问题的输入为
x
ˉ
=
x
+
Δ
x
\bar{x}= x +\Delta x
xˉ=x+Δx,则计算的值为
f
(
x
ˉ
)
f(\bar{x})
f(xˉ)而非
f
(
x
)
f(x)
f(x), 结果的相对误差除以输入数据的相对误差为:
∣
f
(
x
)
−
f
(
x
ˉ
)
∣
∣
f
(
x
)
∣
∣
x
−
x
ˉ
∣
∣
x
∣
\frac{\frac{|f(x)-f(\bar{x})|}{|f(x)|}}{\frac{|x-\bar{x}|}{|x|}}
∣x∣∣x−xˉ∣∣f(x)∣∣f(x)−f(xˉ)∣
这个比例测量了一个函数对于输入数据的误差或者改变的敏感性程度。 这导致一个特定问题 f f f的条件数的数学定义。
Def 3. 一个问题 f f f关于输入数据 x x x的条件数定义为
C f ( x ) = lim ϵ → 0 + sup ∥ δ x ∥ ≤ ϵ ∥ f ( x + δ x ) − f ( x ) ∥ ∥ f ( x ) ∥ ∥ δ x ∥ ∥ x ∥ . C_f(x)=\lim _{\epsilon \rightarrow 0^{+}} \sup _{\|\delta x\| \leq \epsilon} \frac{\frac{\|f(x+\delta x)-f(x)\|}{\|f(x)\|}}{\frac{\|\delta x\|}{\|x\|}} . Cf(x)=ϵ→0+lim∥δx∥≤ϵsup∥x∥∥δx∥∥f(x)∥∥f(x+δx)−f(x)∥.
例1. 寻求下面三个函数的条件数
a.
f
(
x
)
=
x
2
,
C
f
(
x
)
=
∣
x
∣
∣
2
x
∣
/
∣
x
2
∣
=
2
f(x)=x^2, C_f(x)=|x||2 x| /\left|x^2\right|=2
f(x)=x2,Cf(x)=∣x∣∣2x∣/
x2
=2, 因此
f
f
f 是 well-conditioned.
b.
f
(
x
)
=
1
/
(
1
−
x
)
,
C
f
(
x
)
=
∣
x
∣
∣
1
/
(
1
−
x
)
2
∣
/
∣
1
/
(
1
−
x
)
∣
=
∣
x
/
(
1
−
x
)
∣
.
f
(
x
)
f(x)=1 /(1-x), C_f(x)=|x|\left|1 /(1-x)^2\right| /|1 /(1-x)|=|x /(1-x)| . f(x)
f(x)=1/(1−x),Cf(x)=∣x∣
1/(1−x)2
/∣1/(1−x)∣=∣x/(1−x)∣.f(x) 是ill-conditioned 在
x
=
1
x=1
x=1 附近,并且是 well-conditioned在其他任何地方.
c.
f
(
x
)
=
e
x
,
C
f
(
x
)
=
∣
x
∣
∣
e
x
/
e
x
∣
=
∣
x
∣
.
f
(
x
)
f(x)=e^x, C_f(x)=|x|\left|e^x / e^x\right|=|x| . f(x)
f(x)=ex,Cf(x)=∣x∣∣ex/ex∣=∣x∣.f(x)对于大的
x
x
x是 ill-conditioned.
(b) 和 (c) 表明在
x
x
x的特定范围内,
x
x
x 相对小的改变将引起
f
(
x
)
f(x)
f(x)的计算的巨大误差.
定义4. 矩阵 A A A的条件数定义为 ∥ A ∥ ∥ A − 1 ∥ \|A\|\left\|A^{-1}\right\| ∥A∥ A−1 ,表示为 κ ( A ) \kappa(A) κ(A). ∥ ⋅ ∥ \|\cdot\| ∥⋅∥表示任意的矩阵范数.
定义5. 矩阵 A A A是ill-conditioned如果 A A A的条件数很大(large);否则 A A A是well-conditioned.
当然,这里的large是模糊的,条件数如果是在10^4或者更大的范围内则肯定是ill-conditioned,但对于一些矩阵而言,一个较小的条件数也可能表示ill-conditioned,决定矩阵是否是ill-conditioned并不是一门准确的科学。
cond(A); % 2-norm
cond(A,1); % 1-norm
cond(A,'inf'); % infty-norm
cond(A,'fro'); % Frobenius-norm