-
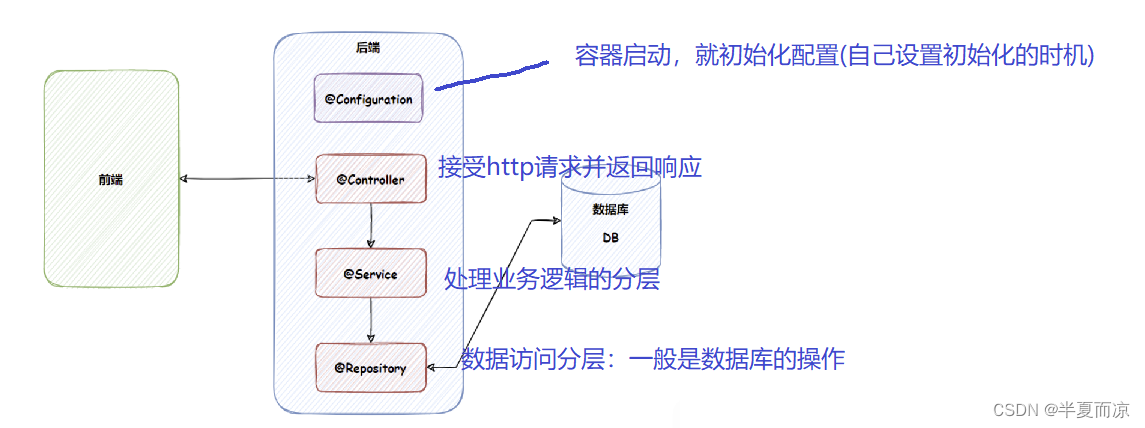
求k++频度 K=0; for(i=1;i<=n;i++) 假如是1——8,执行了9次,8次有效,最后一次无效 for(j=i;j<=n;j++) k++ 我的理解: 假设n为8 我们看k++频度实际上就是看内圈for的有效循环次数 第一轮是1——8 八次有效循环 第二轮是2——8 七次有效循环 第三轮是3——8 六次有效循环 第四轮是4——8 五次有效循环 第五轮是5——8 四次有效循环 第六轮是6——8 三次有效循环 第七轮是7——8 二次有效循环 第八轮是8——8 一次有效循环 如果数字n很大,没有时间画到循环结束 8-1+1 8-2+1 8-3+1 8-4+1 ... 8-8+1 n-i+1就是规律你只需要把前面几次循环的次数求出来,把最后几次循环的次数求出来,基本上都可以用等差求和公式计算出结果
所以上面的每次的执行次数相加就是 1+2+3+....n =[n(n+1)]/2 次 时间复杂度是O(n^2) -
数据元素是数据的基本单位
-
顺序表,删除表尾元素,时间复杂度是O(1)
-
顺序表,删除表头元素,时间复杂度是O(n)
-
长度为n的顺序表,删除某一个元素,平均需要移动(n+1)/2个元素
-
长度为n的顺序表,删除第i个元素,需要移动n-i个元素
-
长度为n,n表示元素个数,下图n为6,删除第i个,下图i是第3个元素,那就要移动i+i到n这些元素,所以移动n-i个元素

-
入栈push(&S,e),是将e这元素插入到栈顶
-
A有3个兄弟,B是A的双亲,B的度是4

-
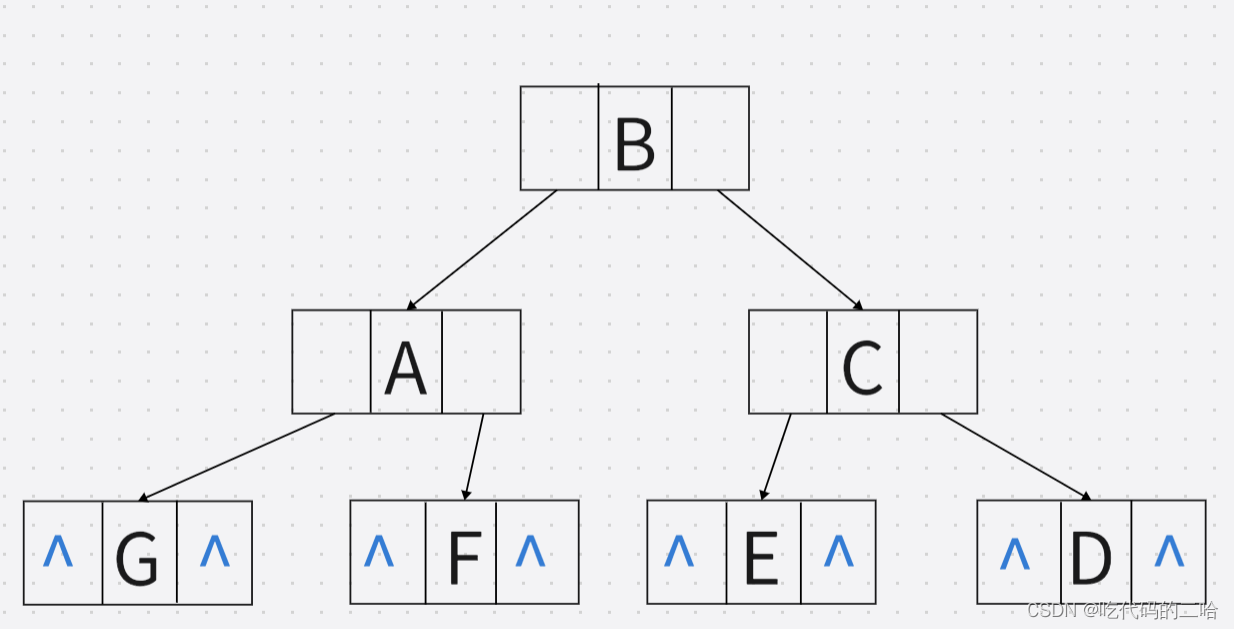
含有1000个节点的二叉链表中有几个空链域
我的理解:下图有7个节点,每个节点2个指针域,7个节点要6个指针域连接起来,那1000个节点,就有2000个指针域,其中1000个节点需要999个指针域来连接,那就剩下2000-999个节点是空的也就是1001个节点是空的,n个节点的二叉链表,有n+1个空链域
-
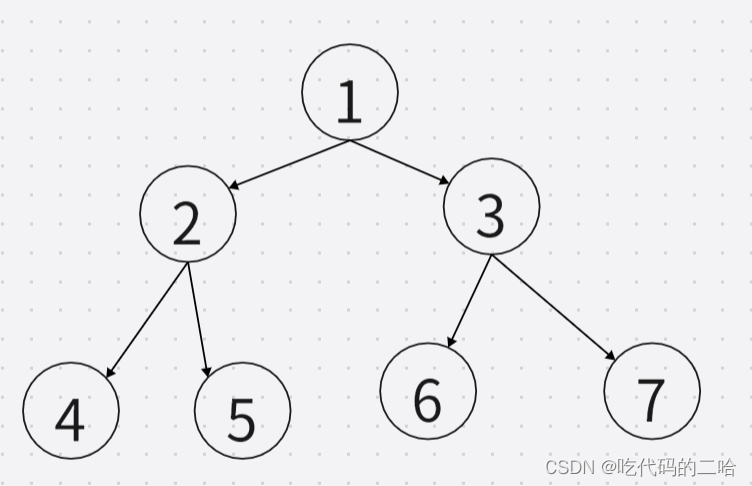
深度为10的满二叉树有几个节点:1023个
我的理解:满二叉树,就是编号从上至下,从左至右,变大
除了最后一层有叶子节点,其他层的子节点都是两个,深度为k的满二叉树的节点总数是(2^k)-1
第i层上有2^(i-1)个节点,满二叉树的叶子节点有
2 ^ (k-1)个
-
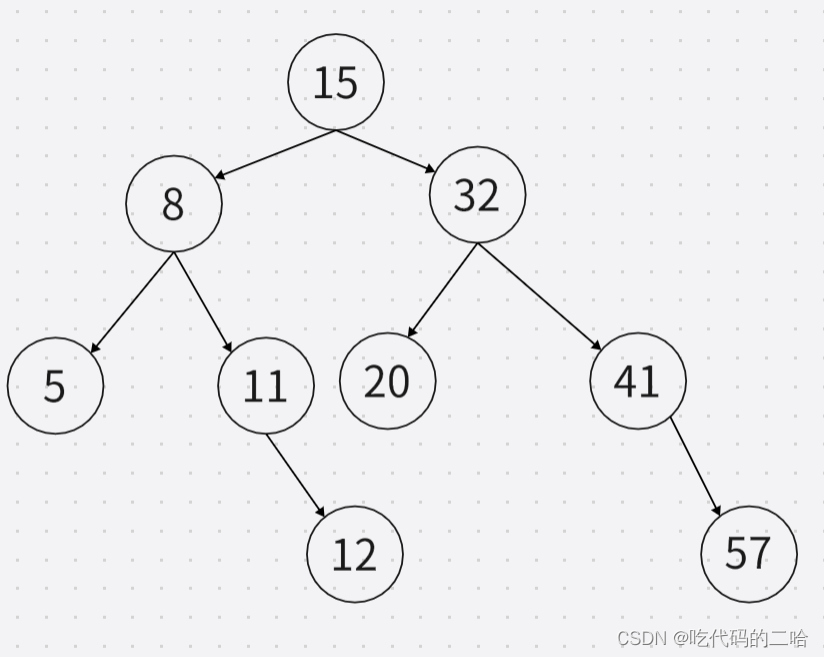
静态查找中的折半查找,找到20需要几次
{5,8,11,12,15,20,32,41,57}
我的理解:一共9个数,下标从0到8
先找第一个数(0+8)/2向下取整还是为4,下标为4的数是15,是找的第一个数,20比它大,就从15的右边开始
第二次找,依然是下标带入计算,(5+8)/2向下取整为6,下标为6的数是32,20比他小
第三次找(5+5)/2向下取整为5,下标为5的就是20,找了3次
-
循环队列
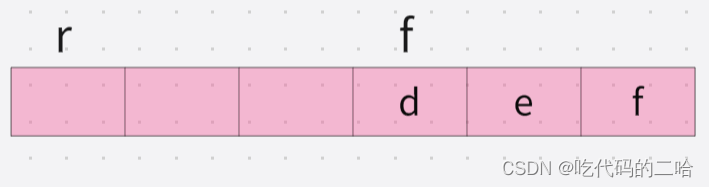
1.判断队列满(r,f是下标)
看图下,r的位置不能放元素,是一个队列满状态,队列满的公式是(r+1)%Maxsize==f
Maxsize表示有几个格子
下图Maxsize=6,f=0,r为5,(5+1)%6=0
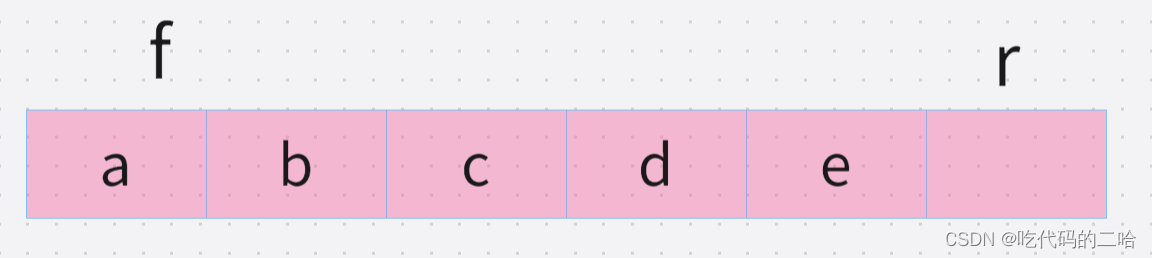
队列为空时 r==f
进来一个元素,先判断队列是否满
没满就 r=(r+1)%Maxsize
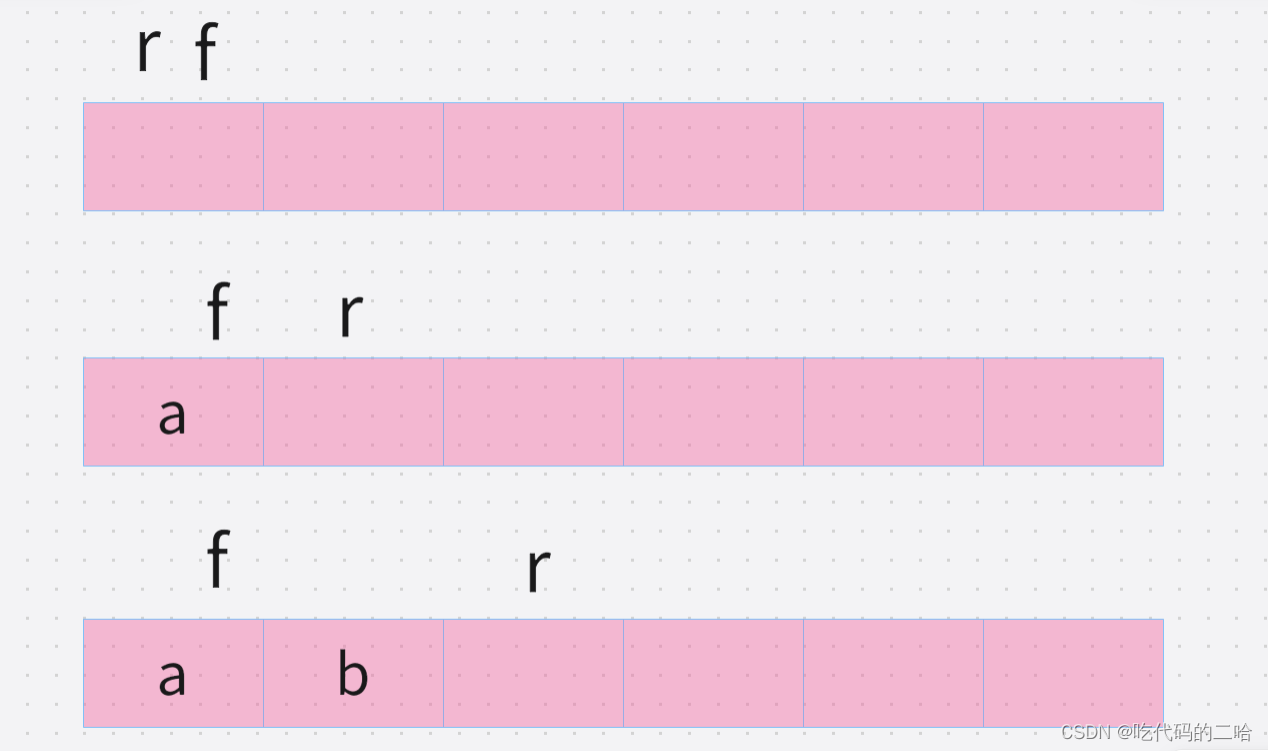
出队,先判断队列是否为空,队列为空拿什么出队
不为空
f=(f+1)%Maxsize
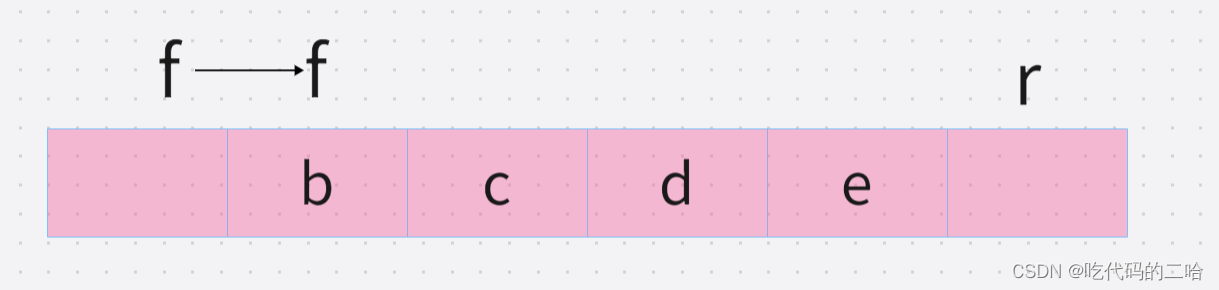
判断某一时刻循环队列的长度,也就是求队列中元素个数
如果r>f (r,f是下标)
就用r-f
5-3=2
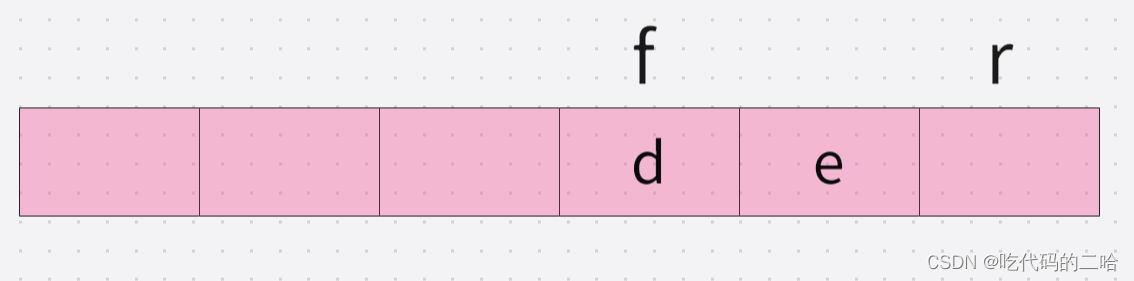
如果此时r<f
就用r-f+Maxsize
0-3+6=3
中和上述两种情况
公式就是(r-f+Maxsize)%Maxsize
-
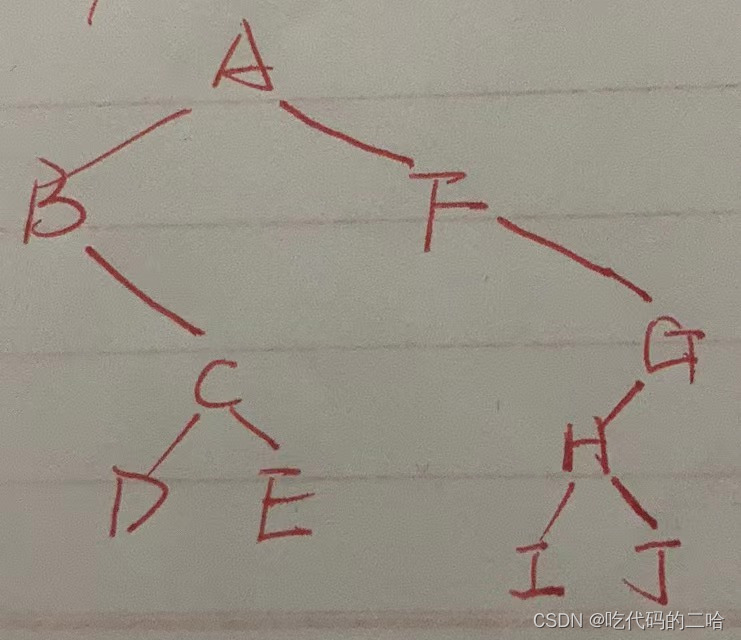
某二叉树的中序遍历为BDCEAFIHJG,后序遍历为DECBIJHGFA,画出二叉树,然后写出先序遍历
先序遍历:ABCDEFGHIJ
-
八个权值构造哈夫曼树{30,70,15,10,20,35,50,60},求带权路径长度

-
将深林转换为二叉树 节点左边是孩子,右边是兄弟
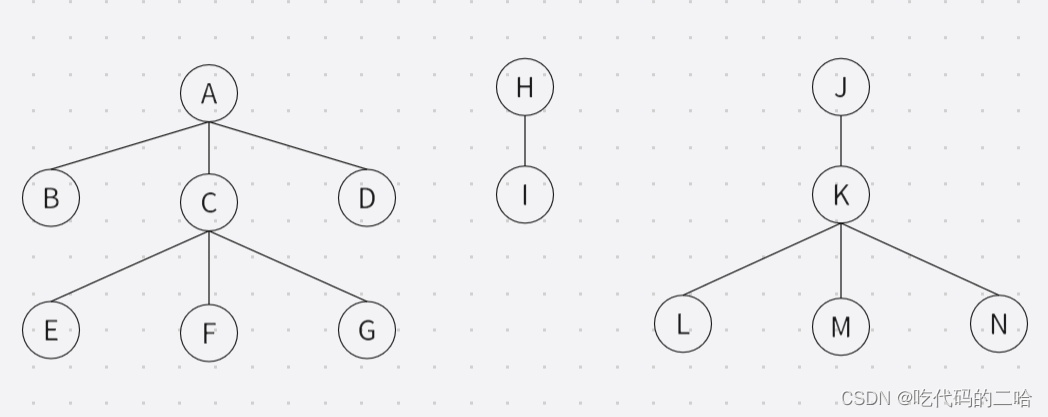
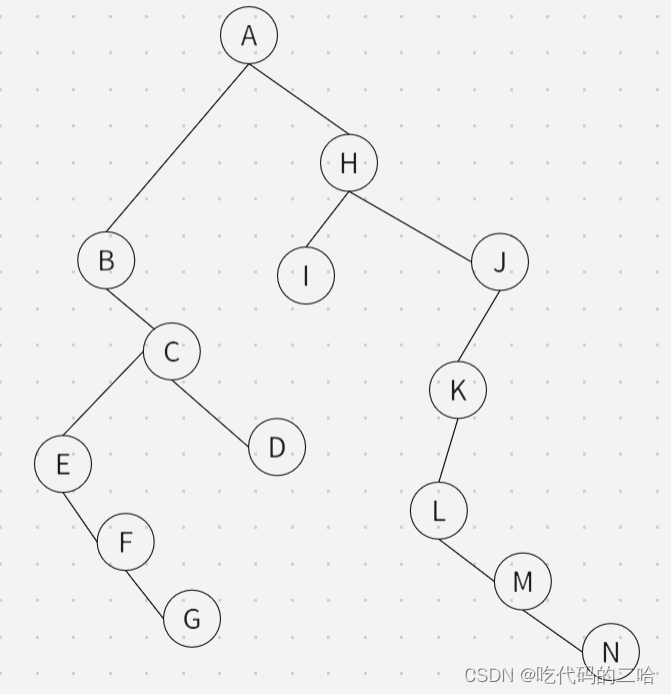
-
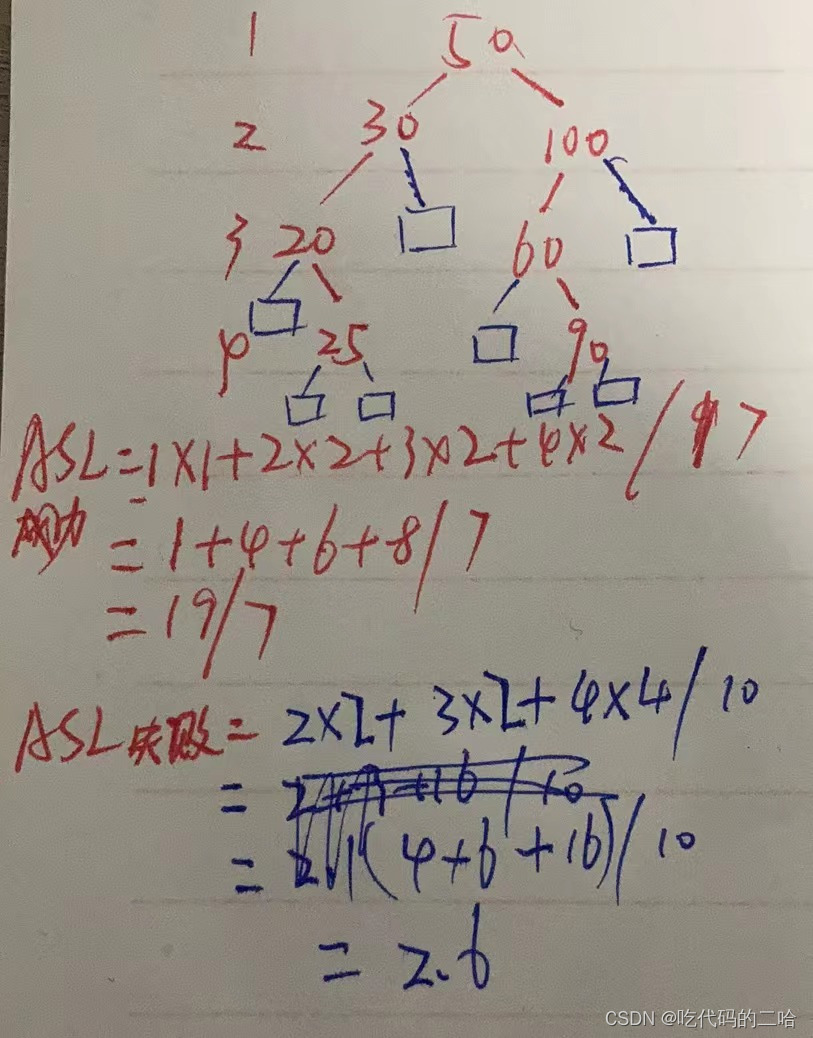
关键字序列{50,100,60,50,30,20,25,30,90}构造二叉排序树,求查找平均长度(相同的数字,如果已经在图中,就不用再进入图中了)
-
一组关键字序列构造哈希表{19,14,23,1,68,20,84,27,55,11,10,79}哈希函数为
H(key)=key MOD 11,表长为11,采用链接地址冲突法
我的理解:用每一个数去与11取模
19%11=8 19在下标为8的格子下面,

14%11=3 则14在下标为3的位置
如果遇到一个数25,25%11=3 25也在下标为3的位置,这里就用冲突解决办法,题目的冲突解决办法是链接地址冲突法就是把25放在14下面

重复上面的步骤 结果如下
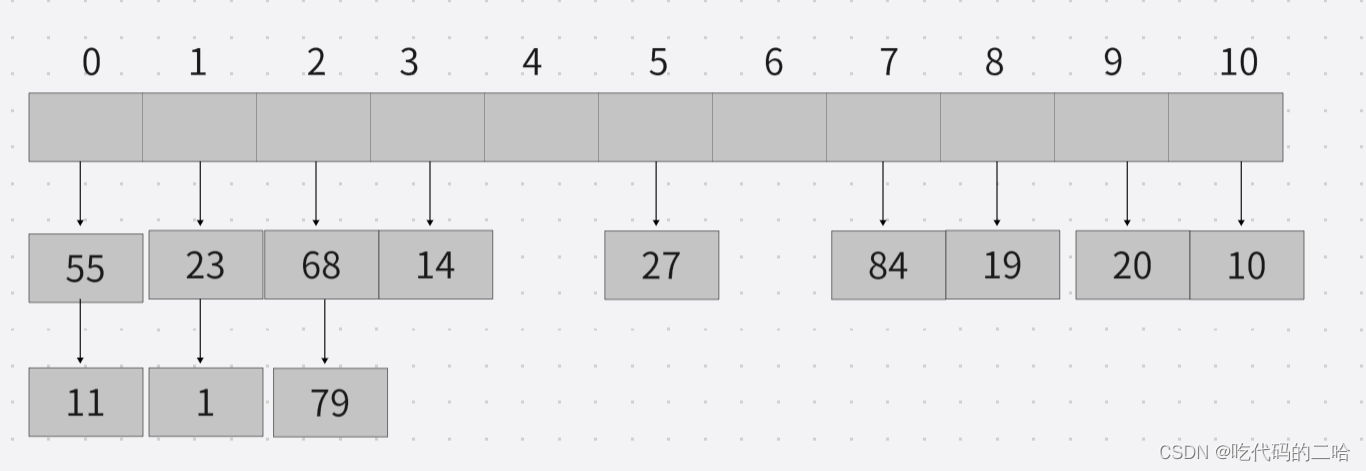
ASL成功: 蓝色的框里的9个元素只查找1次就找到,红色框里的3个元素查找2次就找到 求的是每个元素的查找平均率嘛,除元素总个数 ASL成功=(1x9+2x3)/12=1.25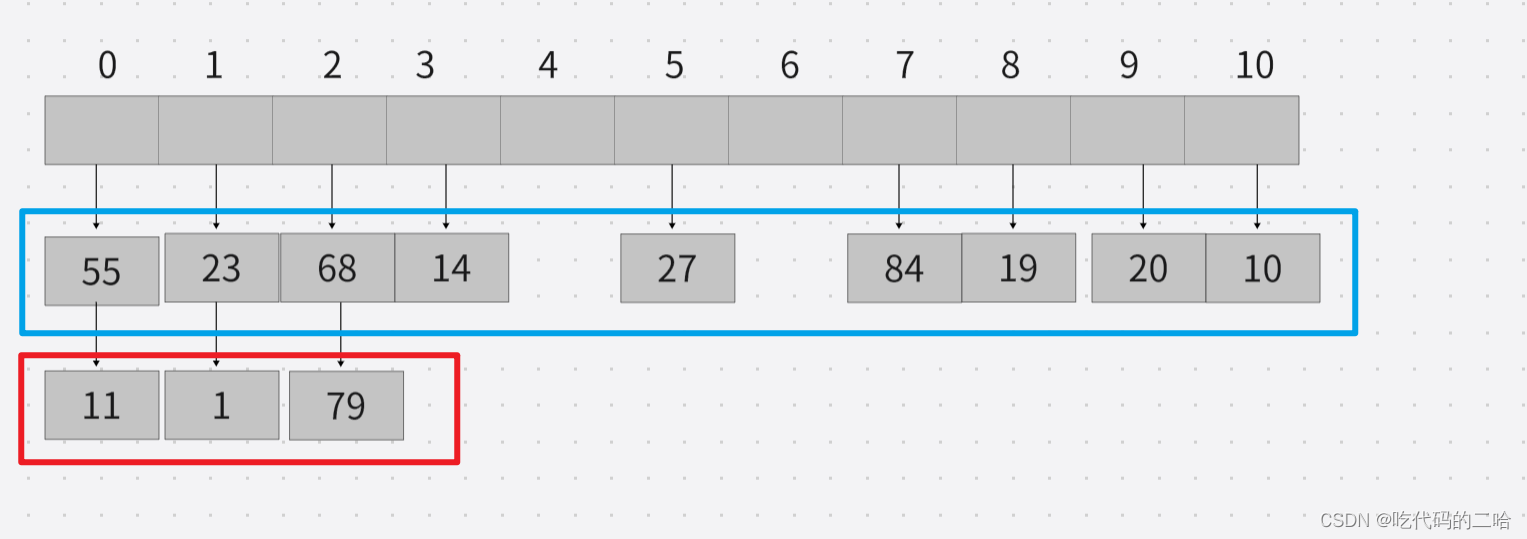
ASL失败: 0号格子找第三次时才为空,所以第一个格子下标为0的查找失败为3 ASL失败=(3+3+3+2+1+2+1+2+2+2+2)/11 这里注意: 查找失败要除表长 查找成功要除元素个数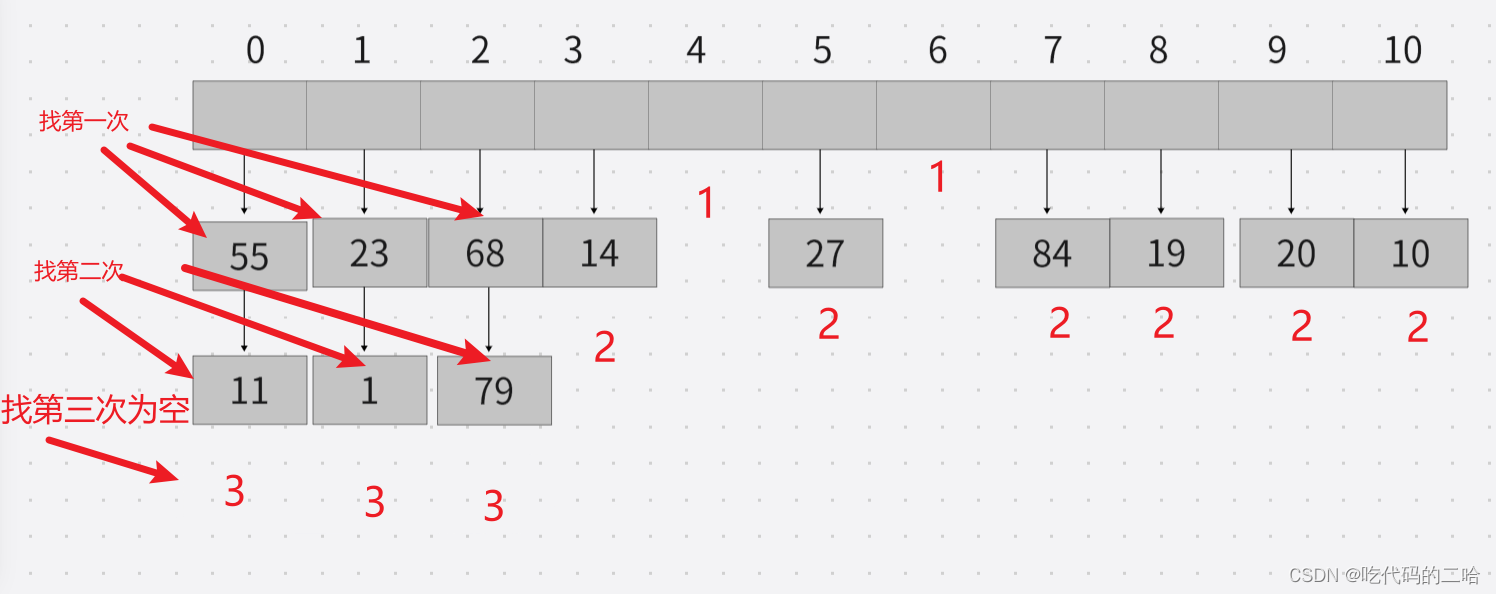
-
下图是无向图的邻接表
从C开始求深度优先
从C开始求广度优先
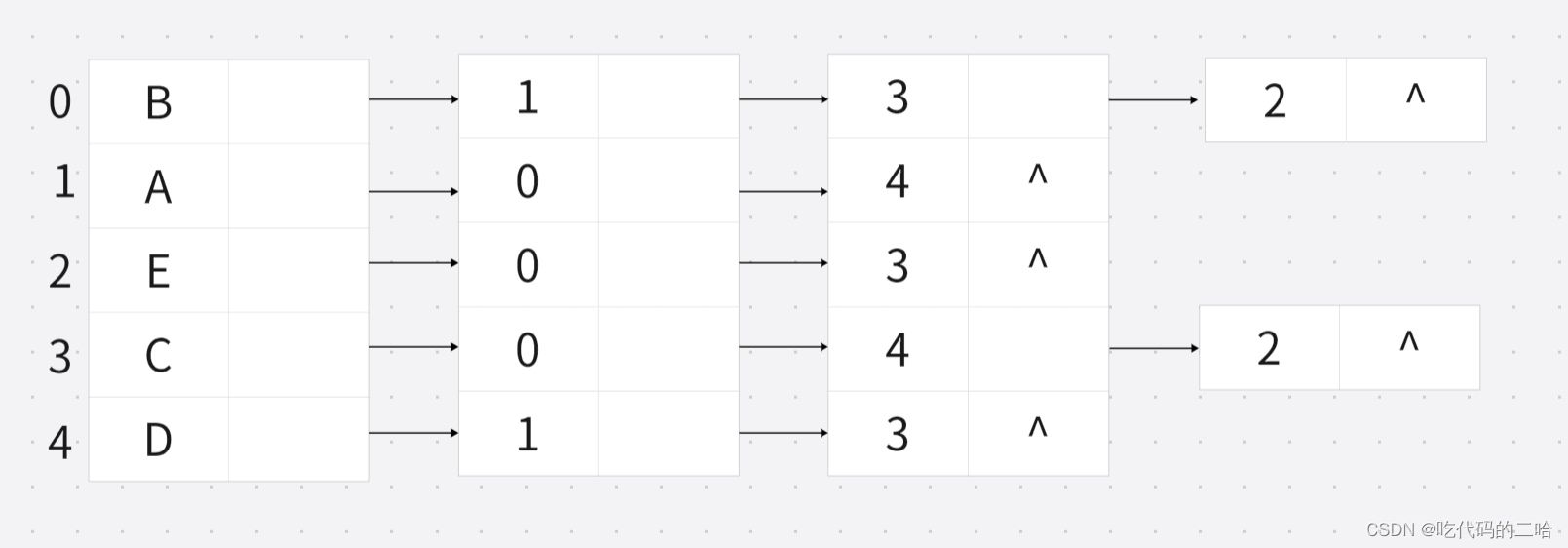
深度优先就是一条路走到黑,到黑了就退一步,又走到黑
深度优先:C——B——A,再从A返回到B,从B的第二个节点继续走到底,B的第二个节点是3,C是不是3,也被访问过了,再去找B的第三个节点,B的第三个节点是2,2代表E,E之前没被访问过,所以接在序列后面就是C——B——A——E,E的第一个节点是0,已经被访问了,E的第二节点是3也被访问了,所以从E退回到B,B的节点是不是被访问完了,所以从B退回到C,接着去找C的第二个节点,没有问题吧。C的第二个节点是4,也就是D,D之前没被访问,所以接在序列后面就是C——B——A——E——D
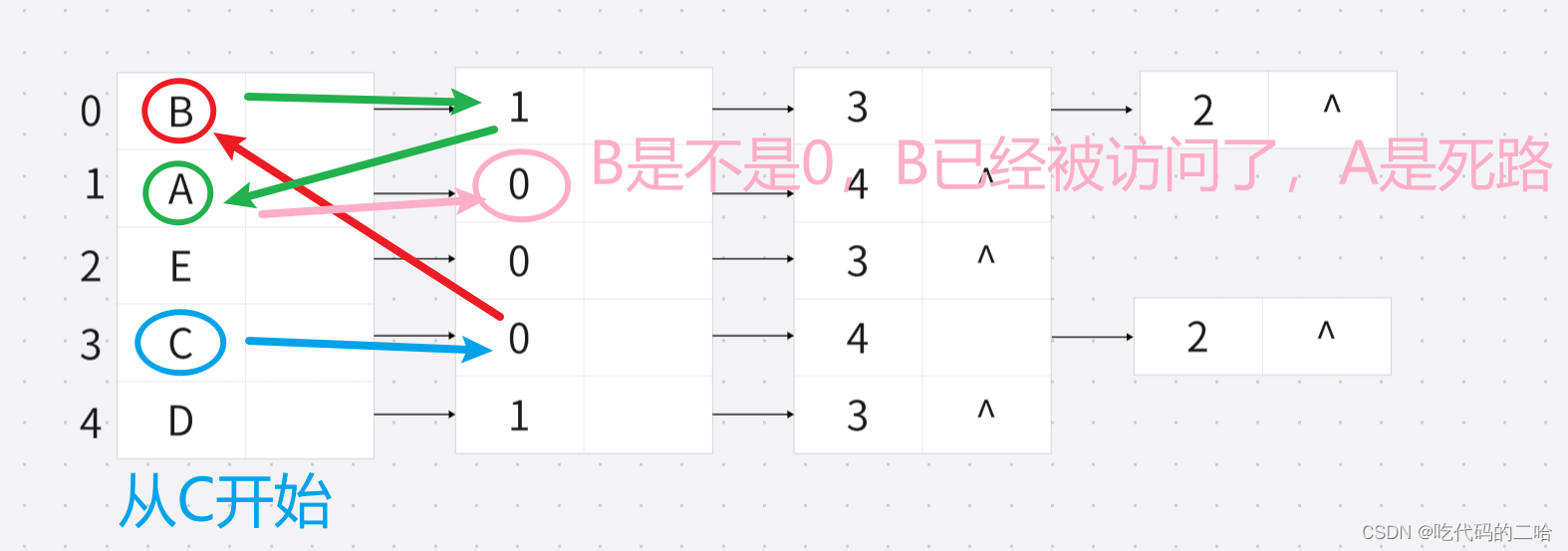
我理解的深度优先,从A开始,我画的这种深度优先遍历只是其中一种,还有很多种走法,蓝色是走,红色是遇到死胡同就回退
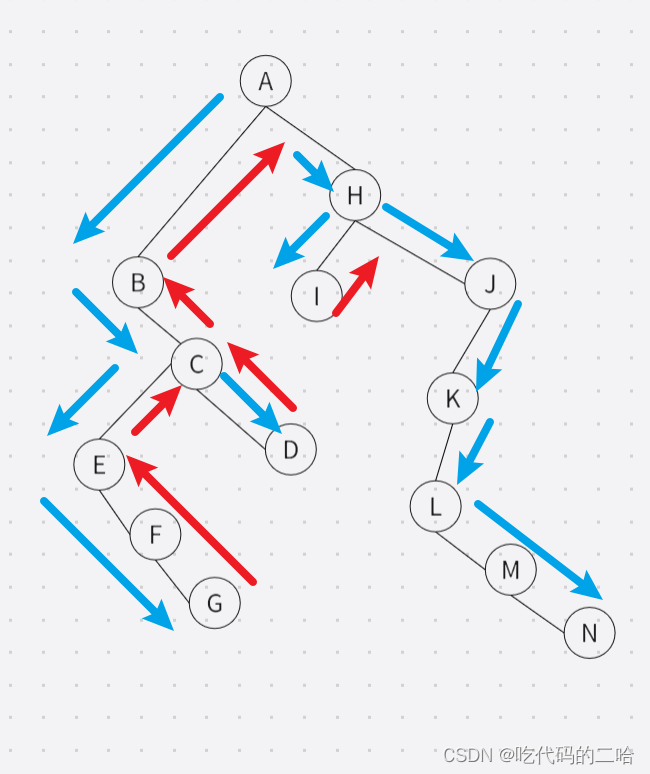
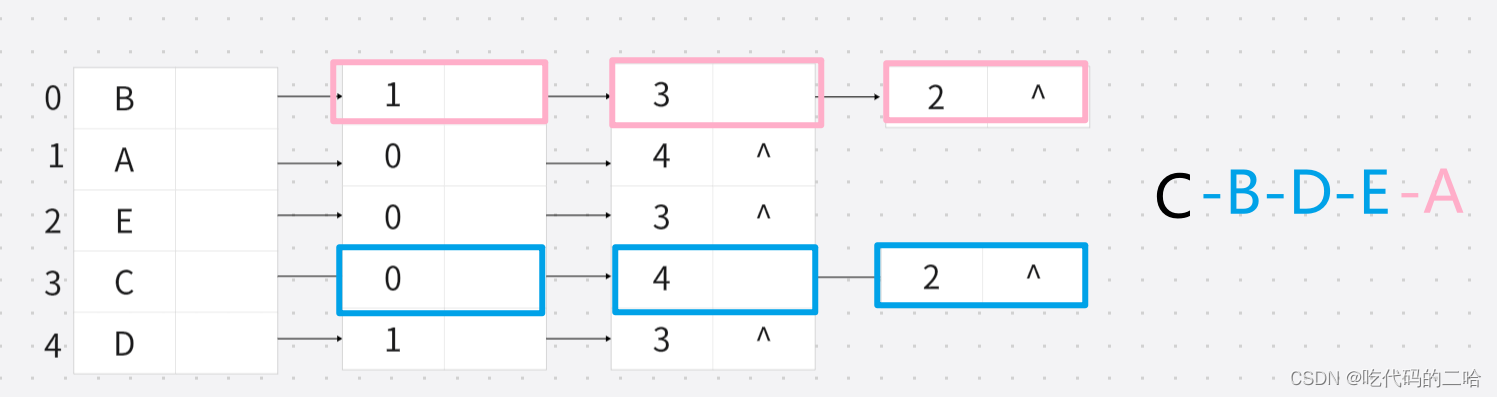
下图 广度优先:C先看见了三个元素,C——B——D——E,B中又看见了A
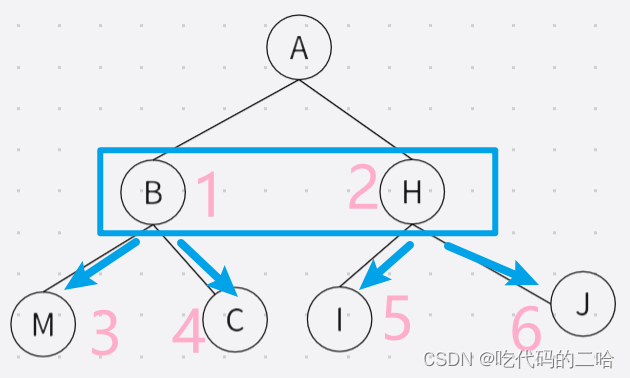
广度优先比较简单,A先看见了B和H,则序列为A——B——H。先看的B,后看见的H,那I,J写在M,C后面 序列号为A——B——H——M——C——I——J
-
快速排序:
快速排序以第一个或者最后一个数为基准,我取第一个数为基准,大于第一个数,去右边,小于第一个数的去左边,
我的理解:大于X的放右边,小于X的放左边,等于X的数,随意放
类似于把棍子掰成左右两段,左段又掰成两段,右段又掰成两段void offcn(int A[],int left,int right)#创建一个方法,数组A,传入left,right { int i=left;我认为:left和right是每次掰成两段的首尾值,下一轮的left和right需要依靠本轮的left和right求得,所以需要i,j来工作 int j=right; int temp=A[left];temp是第一个元素,第一个元素就可以被覆盖,也就是i下标所在的值被覆盖,这样就达到了移动元素排列顺序的目的 while(i<j) { while(i<j&&A[j]>temp) 以中间为分界,在右半部分只要找到一个数小于temp,为什么是temp呢,快速排序以第一个或者最后一个数为基准,我取第一个数为基准,大于第一个数,去右边,小于第一个数的去左边,我在右边找到一个数小于基数temp,我就把这个数覆盖第一个数,记住第一个数是不是已经被temp保存了啊,所以随便覆盖。我在右边找啊找,每个数都大于第一个数,记住右半部分是从右向左找噢,所以j--,左半部分是从左向右找,所以i++,终于找到一个数小于第一个数了,这就表示不满足while循环啊,所以跳出循环啊,执行赋值语句啊。懂了没 j--; A[i]=A[j]; while(i<j&&A[i]<temp) 从左边找出一个大于基数temp,我找啊找,每一个数都小于temp,我继续找,找到了一个数大于temp,我就跳出循环不找了,要把这个大的数赋值到哪里哩,你想想你上面是不是把一个小的数赋值到前面来了,那它是不是可以被覆盖,它在哪,是不是在下标为j的位置。我可没动过j啊,所以之间赋值过去 i++ A[j]=A[i] } A[i]=temp; offcn(int A[],int left ,int i-1); offcn(int A[],int i+1 ,int right); } -
在带头结点的单链表L中的第i个位置前插入元素e
我的理解: L不能动,让工作指针P去移动, 移动到哪里算是个头呢 移动到i的前面就到头了是不是 那就是说假如一个变量不再小于i-1了,这个变量必定在i的左手边 if(j<i-1) p=p.next 但你也不知道要执行几次才找到i的左边,所以p的移动用循环,一直找,直到找到 while(j<i-1) p=p.next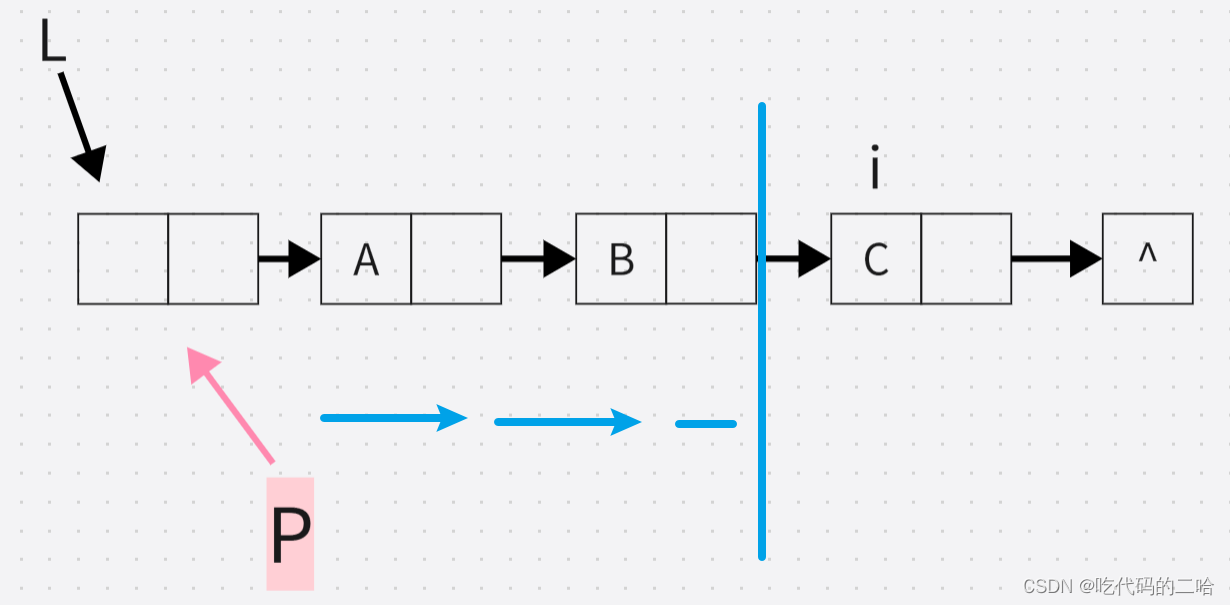
还有一个问题,假如我让你插在单链表L的第1000个位置,可上图没1000个节点怎么办?这种情况下j(j初始为0)永远小于i-1,p走到链表底时,p.next=空,所以当p为空了,再执行就没意义了if(!p) return "i有误" #p不为空,!p就表示空,p都为空了,还没找到i,那i就有问题 得在循环条件里加一个限制语句 while(p&&j<i-1)这里表示p不为空且j<i-1时,p向右移动 p=p.next 让他一直执行,一直执行,执行到不满足条件就代表p指向了i的左边的节点还有一个问题,假如我让你插在单链表L的左边第100个位置,可上图的链表就是从L开始的,L左边没有节点,所以这有问题
if(j>i-1) return “i有误”综合一下
if( !p || j>i-1) return "ERROR";如果找到了,那么P已经指向了i的前驱,
然后插入新节点S:S.next=P.next P.next=S i不是指针,如果p的下一跳先指向s,那i节点就不见啦嘿嘿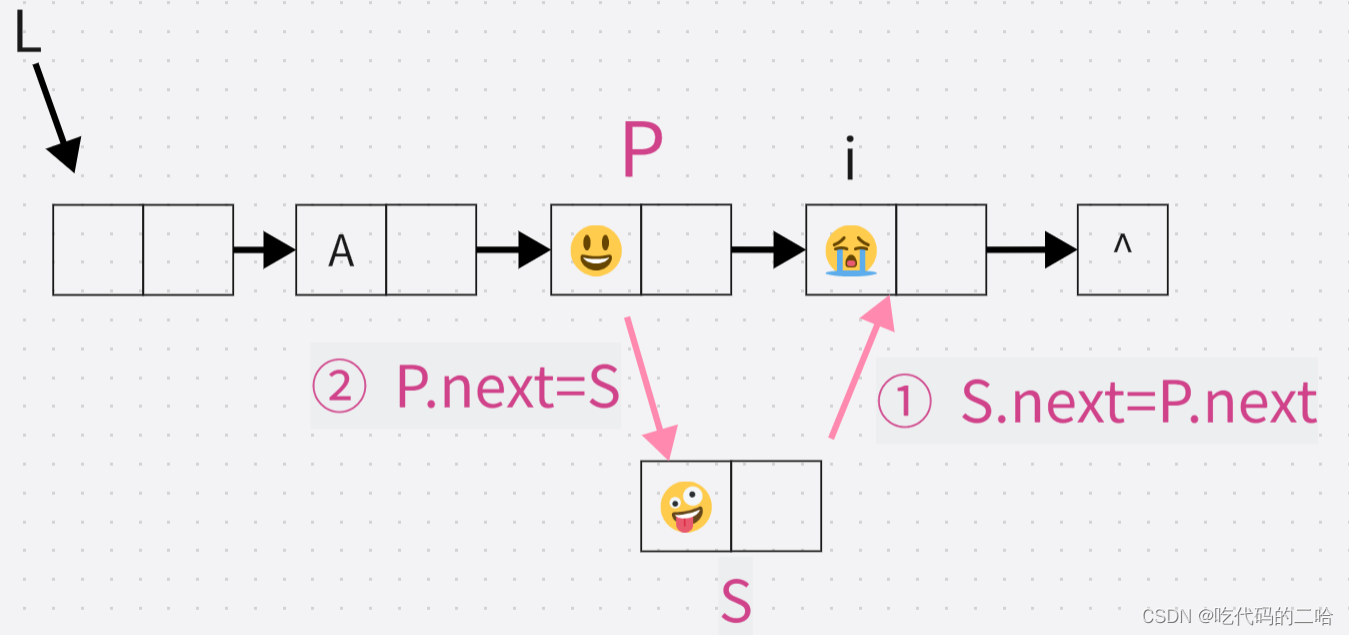
静态查找:1.顺序查找,折半查找,分块查找
-
顺序存储中顺序查找
typedef sturt { Elemtype *elem;我的理解:*elem是一个任意类型的指针 int lenght; 元素个数 }ABC; int search(ABC &L,int key) { int i; L.elem[0].key=key;#将传进来的值放在L.elem顺序表的开头,你也可以放在表尾巴 for(i=L.lenght;L.elem[i].key!=key;--i)#i从顺序表里最后一个元素开始,每一个与x比较 return i; } -
折半查找
typedef sturt { Elemtype *elem;我的理解:*elem是一个任意类型的指针 int lenght; 元素个数 }ABC; int dsfsdsd(ABC &L,int lenght,int key) 长为lenght的顺序表,传进来一个key值 { int min mid max; 小中大,用来折半 min=0; min在最左边 max=L.lenght; max在最右边 while(min<max) min小于max时,可以求中间值 { mid=(min+max)/2; 也可以是mid=min+[(max-min)/2] if(key=L.elem[mid]) return mid; else if(key>L.elem[mid].key) 看key在右半部分,还是左半部分 min=mid+1; 只需要改变min,就继续开始新一轮折半 else max=mid-1; } return 0; } -
用函数返回二叉树的叶子节点个数
int count(BiTree T) { int num=0;计数器 if(T==NULL) 没有根 return 0; if(T->lchild==NULL&&T->rchild==NULL)左孩子右孩子都是空自己就是叶子,然后加1 num++; count(T->lchild); 把左叶子节点调进去再判断,左孩子是空就不调进去 count(T->rchild); 把右孩子节点调进去再判断 return num; }