1、背景介绍

目标：将根据用户产生的数据对课程潜在的会员用户（可能产生购买会员的行为）进行预测。

平台的一位注册用户是否购买会员的行为应该是建立在一定背景条件下。相信很少有用户刚刚完成注册不久，就直接购买会员。
一般来讲，促使付费行为发生的原因，往往都建立在用户的活跃度之上。
数据

!wget -nc “http://labfile.oss.aliyuncs.com/courses/764/data_10.zip”
!unzip -o “data_10.zip”

训练数据集包含有 8 个特征项，以及用户是否为会员的标签，数据共计 40000 条。

最后一项会员标签，通过布尔值进行标识。True 当前用户是会员身份，False 代表当前用户不是会员身份。

import pandas as pd

pd.read_excel("user_fit.xlsx").head()

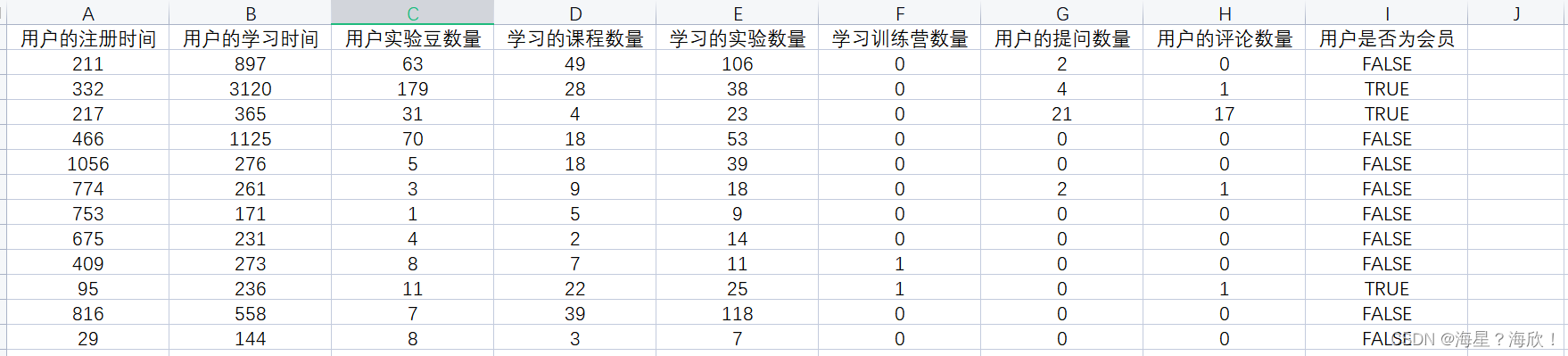
测试数据集包含 10000 条数据，且数据特征项与训练数据集完全一致。唯一不同的地方在于，训练数据集中既有会员数据也有非会员数据，而测试数据集中全部都为非会员用户。

pd.read_excel("user_prediction.xlsx").head()

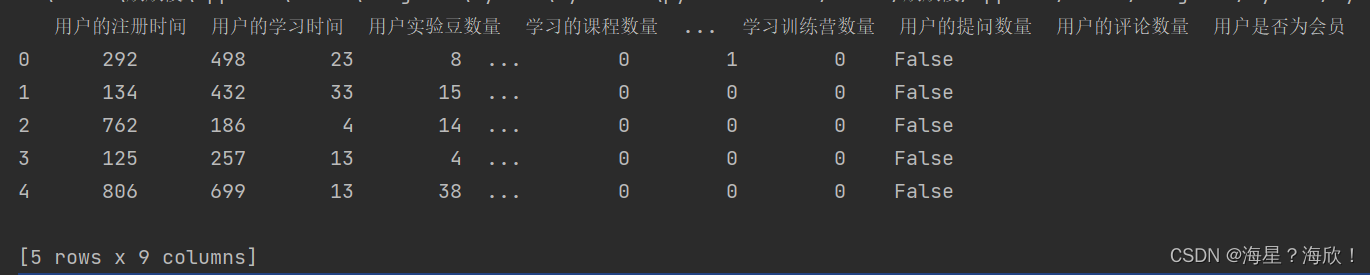
**目标：**预测测试集中这些用户哪些是潜在用户，很可能购买会员的
这些数据已经是处理好的，没有缺失值的数据

2、朴素贝叶斯

2.1 模型介绍

朴素贝叶斯是一种可用于构建分类模型的方法，他是假设特征相互独立的情况下，运用贝叶斯定理进行后验概率计算的简单分类器。

贝叶斯公式：

数据集拥有 8 个特征值，分别为：用户的注册时间、用户的学习时间 用户实验豆数量、学习的课程数量、学习的实验数量、学习训练营数量 用户的提问数量、用户的评论数量。这些特征之间是相互独立的。

而这些特征可能会对最后的目标参数，也就是该用户是否为会员造成影响。也就是说，如果我们现在有一个会员的数据，我们知道他的 8 个特征取值，最后想了解他成为会员的概率有多大？

根据贝叶斯定理，且特征之间相互独立，得到：

像 P(用户的注册时间)P(用户的注册时间) 这样的概率怎样求解呢？由于我们这里是连续变量，一般会针对其进行离散化处理，也就是通过假定一个区间，计算变量落在该区间内的概率。
最后，我们就可以计算出该用户是会员和不是会员的概率，通过比较得出分类属性。

2.2 模型实现

直接使用 scikit-learn 提供的贝叶斯算法来构建模型

scikit-learn 针对朴素贝叶斯提供了三种分类器，分别是：

• 高斯分布朴素贝叶斯分类器 naive_bayes.GaussianNB
• 多项式分布朴素贝叶斯分类器 naive_bayes.MultinomialNB
• 伯努利分布朴素贝叶斯分类器 naive_bayes.BernoulliNB

其中，高斯分布模型常用于特征值为连续型变量的数据集中，例如本实验中的数据集。高斯模型的特点在于它通常假设是这些连续数值为高斯分布，相比于直接把连续变量离散化的方法更优。
伯努利模型常用处理特征变量为布尔值类型的数据集，
多项式模型常用于文本分类。

尝试使用高斯分布朴素贝叶斯针对 user_fit.xlsx 数据集构建一个分类模型：

from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB

# 使用 Pandas 读取数据
df_fit = pd.read_excel("user_fit.xlsx", header=0)
# 特征
X = df_fit.iloc[:, 0:8]
# 目标
y = df_fit['用户是否为会员']
# 安装 3:7 切分验证集和训练集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
X_train.shape, X_test.shape, y_train.shape, y_test.shape

# 构建高斯贝叶斯分类器
model_GaussianNB = GaussianNB()
# 使用训练集训练模型
model_GaussianNB.fit(X_train, y_train)
# 使用验证集评估准确度
model_GaussianNB.score(X_test, y_test)

91%的准确率，可以接受，下面继续训练模型，并且保存为二进制文件

from sklearn.externals import joblib

model_GaussianNB.fit(X, y)
# 保存模型
joblib.dump(model_GaussianNB, 'model_GaussianNB.pkl')

将该模型去评估 user_prediction.xlsx 非会员数据集中，潜在会员用户的概率：

# 使用 Pandas 读取数据
df_pred = pd.read_excel("user_prediction.xlsx", header=0)
# 特征
X_pred = df_pred.iloc[:, 0:8]
# 加载模型
model_GaussianNB = joblib.load('model_GaussianNB.pkl')
# 返回预测概率（%）
results = model_GaussianNB.predict_proba(X_pred) * 100
results

import numpy as np
# 将预测概率转换为 DataFrame
results_df = pd.DataFrame(np.around(results, 2), columns=['非会员概率', '会员概率'])
# 将预测概率添加到原数据集中最后一列
df_merged = pd.concat(
    [df_pred.drop("用户是否为会员", axis=1), results_df['会员概率']], axis=1)
df_merged.sort_values(by="会员概率", ascending=False)

可以看到， DataFrame 最后一列已经添加了我们预测某位用户是潜在会员用户的概率。可以针对概率排序，将大于 50%的用户筛选出来，对这些潜在会员用户给予重点关照。

3、人工神经网络

除了使用高斯贝叶斯分类器，还可以使用人工神经网络来进行预测
同样，首先拿 user_fit.xlsx 看一看神经网络模型的分类效果：

from sklearn.neural_network import MLPClassifier

# 构建神经网络分类器
model_MLPClassifier = MLPClassifier(
    activation='logistic', max_iter=1000, hidden_layer_sizes=(50, 50, 50))
# 使用训练集训练模型
model_MLPClassifier.fit(X_train, y_train)
# 使用验证集评估准确度
score_trainset = model_MLPClassifier.score(X_train, y_train)*100
score_testset = model_MLPClassifier.score(X_test, y_test)*100

print("训练集预测准确率：%.2f%%" % score_trainset)
print("测试集预测准确率：%.2f%%" % score_testset)

使用最常见的 logistic 激活函数，建立一个含 3 个隐含层，每层 50 个神经元的网络。由于迭代次数较多，在线上实验环境中运行时间较长，你也可以调低数值用于测试。
使用全部数据进行训练，对非会员数据进行概率预测：

model_MLPClassifier.fit(X, y)
# 返回预测概率（%）
results = model_MLPClassifier.predict_proba(X_pred) * 100
# 将预测概率转换为 DataFrame
results_df = pd.DataFrame(np.around(results, 2), columns=['非会员概率', '会员概率'])
# 将预测概率添加到原数据集中最后一列
df_merged = pd.concat(
    [df_pred.drop("用户是否为会员", axis=1), results_df['会员概率']], axis=1)
# 按会员概率降排序
df_merged.sort_values(by='会员概率', ascending=False)