1 LBM简介

格子玻尔兹曼法（Lattice Boltzmann Method）简称LBM，是一种CFD算法，可求解流动、传热等常见CFD问题。

LBM基于格子玻尔兹曼方程（LBE），从介观尺度（mesoscope）描述了流体运动。LBE的通用表达形式为：

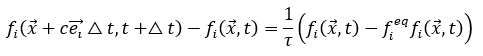
式中，左边为迁移项（streaming term），右边为碰撞项（collision term），fi 为粒子分布函数。

对粒子分布函数进行积分处理，可得流体密度、宏观流体速度、流体压力等宏观物理量。

2 应用领域

目前CFD的主流算法还是有限体积法（FVM）。LBM应用相对较少，但呈现上升态势，特别是气动声学等对湍流计算准确性要求较高的领域。

商用领域，目前较成熟的LBM商用产品有：

• 达索PowerFlow

• 澳汰尔UltraFluidX

达索PowerFlow的汽车气动噪声仿真（图源：engineering.com）

相对于FVM，LBM优势在于：

1 湍流计算准确性更好

FVM常用离散格式均存在不同程度的数值耗散。LBM的数值耗散不明显，湍流计算效果更好。

2 并行性能更好

由于LBM是线性方程，且各个部分耦合较弱，其并行性能更优，且适合于GPU运行。FVM中必须要处理强非线性的对流项，在相同空间离散分辨率下，LBM运行速度远快于FVM。

3 前处理更简单

LBM的空间离散单元为格子，其空间离散形式为四面体或类似于笛卡尔网格的六面体。LBM的前处理无需进行边界层网格划分工作，可显著节约手动工作量，更容易实现前处理自动化。

旋翼气动性能计算的LBM格子分布（图源：Towards NASA’s In House

Lattice-Boltzmann Solver，nasa.gov）

当前LBM主要缺陷在于，高马赫数下计算准确性不足。从数学上来说，基于LBE推导N-S方程，其前提条件为密度变化很小，即低马赫数。