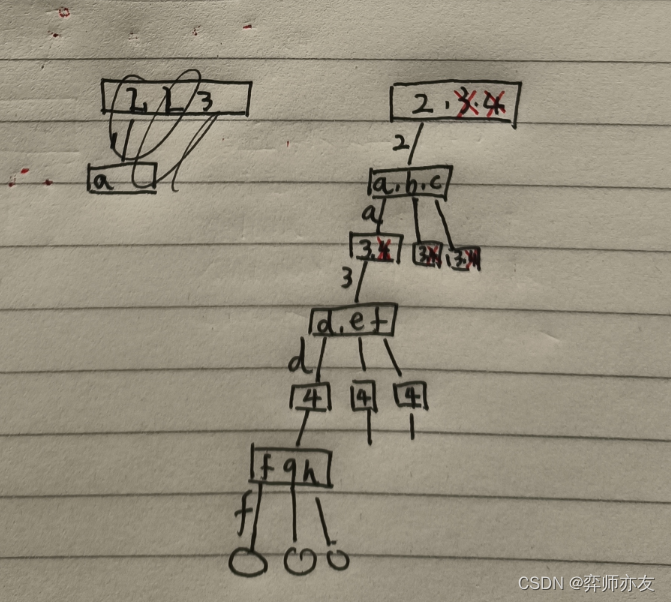
77组合
看完题后的思路
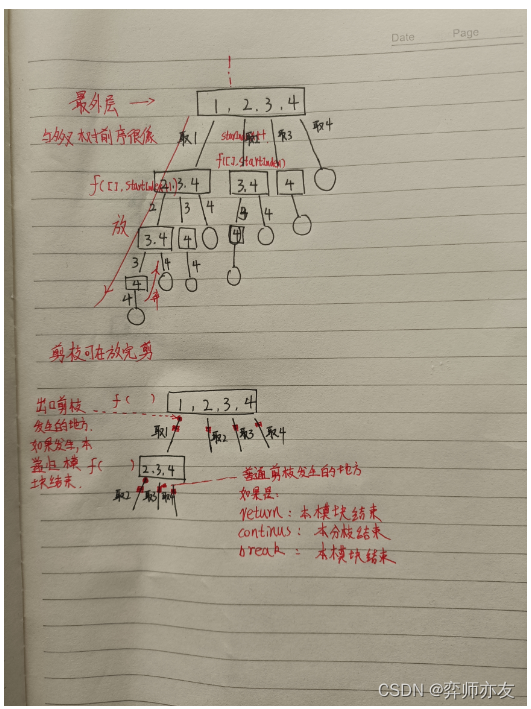
- void f(数组,startIndex)
- 递归终止
if(startIndex数组长度||path.sizek){
if(path.size==k){
加入}
} - 递归
for(;startIndex<num.size;startIndex++){
加入;
4.剪枝
if(path.size>k){
吐出来;
return;
}
f(num,startIndex+1);
// 回溯
吐出来
}
代码
List<List<Integer>> ires = new ArrayList<>();
ArrayList<Integer> ipath = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
combineTB(n,0,k);
return ires;
}
public void combineTB(int n,int startIndex,int k){
//终止
if (startIndex==n||ipath.size()==k){
if (ipath.size()==k){
ires.add(new ArrayList<>(ipath));
}
return;
}
for (; startIndex<n; startIndex++) {
// 尝试加入
ipath.add(startIndex);
// 剪枝
if (ipath.size()>k){ // 这一步永远不会生效,因为终止条件已经剪枝了
return;
}
// 进入下一层
combineTB(n,startIndex+1,k);
// 回溯
ipath.remove(ipath.size()-1);
// 进入本层下一个 ----->
}
}
复杂度
优化:添加剪枝条件
// 剪枝
if (ipath.size()==k||n-startIndex+1<(k-ipath.size())){
return;
}
后一个剪枝条件表示当前可加入的元素<所缺的元素
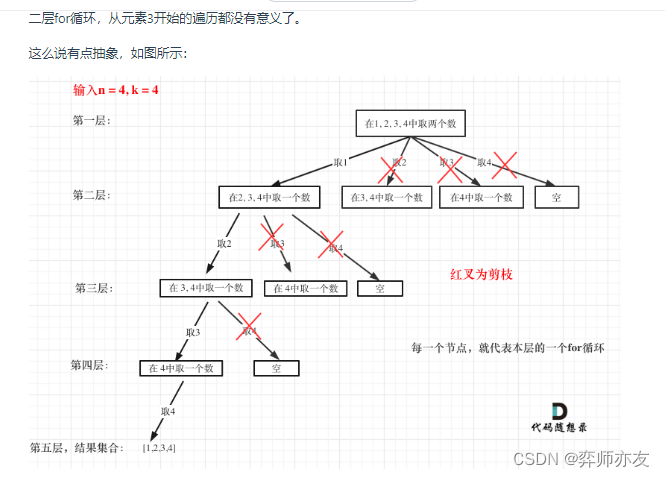
List<List<Integer>> ires = new ArrayList<>();
ArrayList<Integer> ipath = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
combineTB(n,1,k);
return ires;
}
public void combineTB(int n,int startIndex,int k){
//终止
if (startIndex>n||ipath.size()==k){
if (ipath.size()==k){
ires.add(new ArrayList<>(ipath));
}
return;
}
for (; startIndex<=n; startIndex++) {
// 剪枝
if (ipath.size()==k||n-startIndex+1<(k-ipath.size())){
return;
}
// 尝试加入
ipath.add(startIndex);
// 剪枝
// if (ipath.size()>k){
// return;
// }
// 进入下一层
combineTB(n,startIndex+1,k);
// 回溯
ipath.remove(ipath.size()-1);
// 进入本层下一个 ----->
}
}
递归深度: k
递归宽度:n-startIndex+1<(k-ipath.size())
收获
- 三刷看一遍
- 组合问题模板

- 做回溯题步骤
(0)判断问题类型
(1)树状图
(2)递归三部曲
(3)剪枝条件
216.组合总和III
看完题后的思路
a+b=b+a,这是一个组合问题
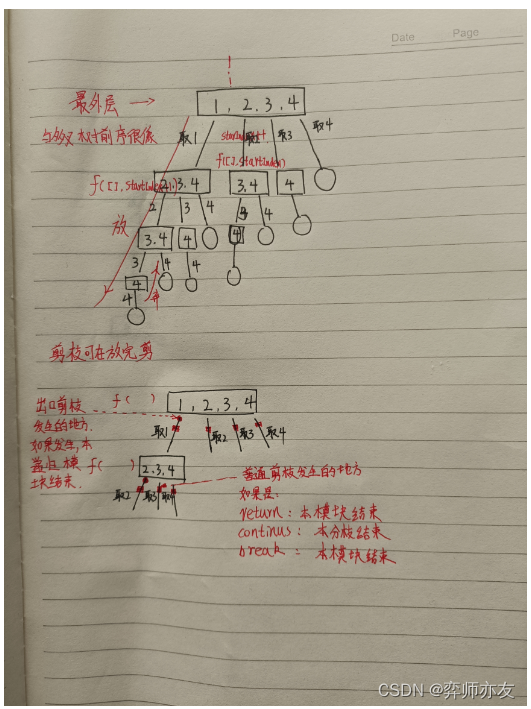
- void f(n,k,startIndex,sum) // 纵向剪枝
- 终止条件
if(path.size==k){
if(和为n){
加入
}
return;
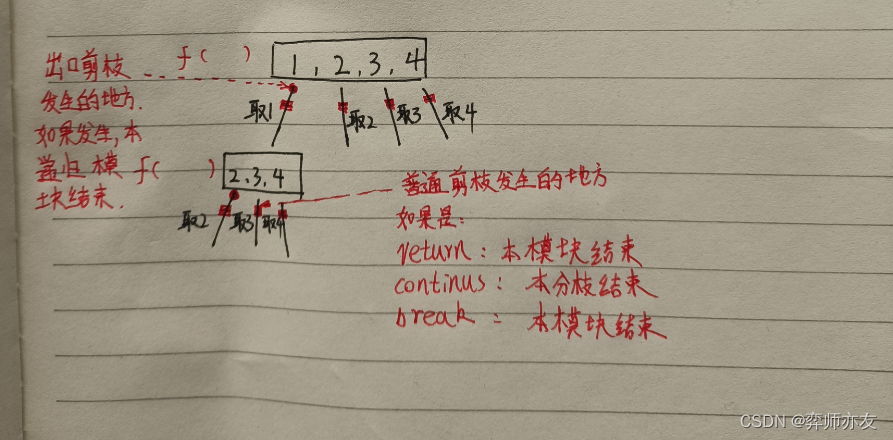
} - 回溯模型
- 剪枝条件
if(path内的数+当前树大于k) return
代码
List<List<Integer>> ires = new ArrayList<>();
ArrayList<Integer> ipath = new ArrayList<>();
//216. 组合总和 III
public List<List<Integer>> combinationSum3(int k, int n) {
combinationSum3BT(k,n,0,1);
return ires;
}
public void combinationSum3BT(int k, int n,int sum,int startIndex ) {
if(ipath.size()==k){// 终止+纵向剪枝
if (sum==n){
ires.add(new ArrayList<>(ipath));
}
return;
}
for (; startIndex <=9 ; startIndex++) {
// 纵向剪枝
if (startIndex+sum>n){
return; // (纵)横向剪枝 因为兄弟节点 (startIndex++)+sum也一定>k
}
sum+=startIndex;
ipath.add(startIndex);
combinationSum3BT(k,n,sum,startIndex+1);
// 回溯
sum-=startIndex;
ipath.remove(ipath.size()-1);
// 本层下一个
}
}
复杂度
最坏时间复杂度 0(9*k)

收获
1.本题让组合剪枝变得明朗,三刷大脑过一遍
2, 组合问题中的纵横剪枝
17.电话号码的字母组合
看完题后的思路
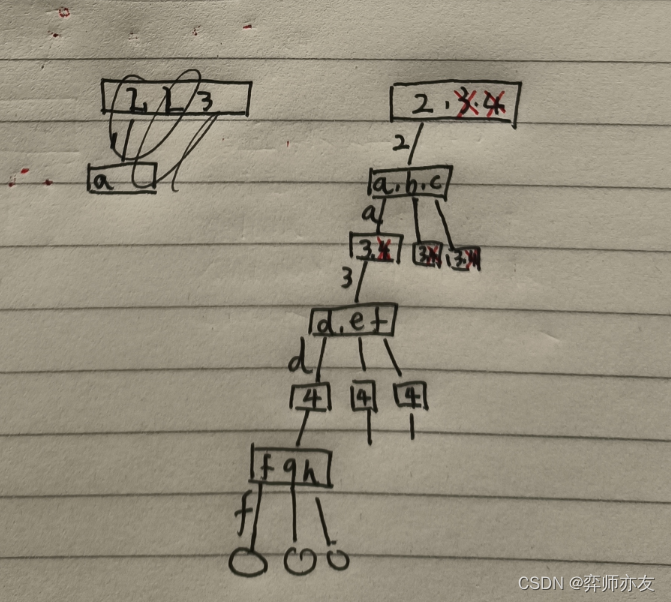
- 本体可以抽象为若干个筐,筐中有若干个球,每次从筐中取一个球,所有可能的球的组合。
本质上是只取组合传统递归树最左边分支 - void f(map<数字,字母>,startIndex,[数字])
- if(ipath.size==数字个数){
加入结果;
return;
} - 回溯算法
num【startIndex】;
取出对应的字母;
for(字母){
加入ipath;
f(map<数字,字母>,startIndex+1,[数字])
回溯;
}
代码
StringBuilder sbPath = new StringBuilder();
ArrayList<String> slistRes = new ArrayList<>();
public List<String> letterCombinations(String digits) {
if (digits==null||digits.length()==0){
return slistRes;
}
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
letterCombinationsBT(digits,numString,0);
return slistRes;
}
public void letterCombinationsBT(String digits,String[] map,int startIndex) {
// 出口
if (sbPath.length()==digits.length()){
slistRes.add(new String(sbPath));
return;
}
// 回溯算法
char c = digits.charAt(startIndex);
String s = map[c - '0'];// 对应的字符组合
// 内部回溯
for (char c1 : s.toCharArray()) {
sbPath.append(c1);
// 下一层递归
letterCombinationsBT(digits,map,startIndex+1); // 关键是startIndex+1
// 回溯
sbPath.delete(sbPath.length()-1,sbPath.length());
// 进入本层下一层
}
}
复杂度
时间复杂度 0(数字个数*(3或4))
收获🐱🚀🐱🚀
1. 三刷在大脑过一遍
2. 本题通过画树竟然完美解决了
3. 若干袋子,求小球组合递归树