目录
题目描述
解题思路:
代码部分:
题目描述
有一个火车站,铁路如图所示,每辆火车从A驶入,再从B方向驶出,同时它的车厢可以重新组合。假设从A方向驶来的火车有n节(n≤1000),分别按照顺序编号为1,2,3,…,n。假定在进入车站前,每节车厢之间都不是连着的,并且它们可以自行移动到B处的铁轨上。另外假定车站C可以停放任意多节车厢。但是一旦进入车站C,它就不能再回到A方向的铁轨上了,并且一旦当它进入B方向的铁轨,它就不能再回到车站C。
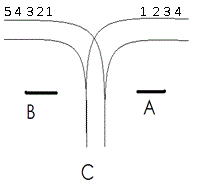
负责车厢调度的工作人员需要知道能否使它以a1,a2,…,an的顺序从B方向驶出,请来判断能否得到指定的车厢顺序。
输入
第一行为一个整数n,其中n≤1000,表示有n节车厢,第二行为n个数字,表示指定的车厢顺序。
输出
如果可以得到指定的车厢顺序,则输出一个字符串”YES”,否则输出”NO”(注意要大写,不包含引号)。
样例输入
5
5 4 3 2 1样例输出
YES解析
解析:观察发现,整个调度过程其实是在模拟入栈出栈的过程,而这个过程中,我们可以分成三种状态:栈前、栈中、栈后。我们可以发现,当某个数字出栈了,说明比它小的数字要么已经出栈了,要么还在栈里,不能是入栈前状态,并且在栈中的顺序是从大到小的(从栈顶往栈底看),比如出5,那么1,2,3,4要么已经在5之前出了,要么还在栈中(假如1,3,4在栈中,从栈顶往栈底看依次为4,3,1),不能是入栈前的状态。如果某个数字要出栈,那么当前在栈中的数字都必须小于它,否则就与栈的性质矛盾,不合法,于是我们可以这样解决:
从第一个数字开始扫描,a[i]表示当前出栈的数字,如果有比a[i]大的数字还在栈中,那么就产生矛盾,输出“NO”;否则,标记当前数字a[i]为栈后状态,那么[1, a[i]-1]这些数字如果还没出栈,标记为栈中状态。具体我们可以用0表示为确定状态,1表示栈中状态,2表示栈后状态。
解题思路:
从指定出栈顺序开始考虑:对其中一个数字:
这个数字有两个来源:一个是火车车头的那个数字直接正好是我想要的,另一个是栈首那个数字正好是我想要的。
归拢一下:火车车头那个数字如果直接正好是我想要的,也可以先在栈里“过水”:先储存在栈首,然后再从栈首提取出来。
这样,来源由二变一:都从栈首提取。
所以,判断的条件就被简化为以下几种:
栈空没空;A方向来的火车被没被使用完;栈首元素是不是我想要的。
从而,题目可以分为以下几种情况:
1.如果栈没空&&栈首元素就是我想要的->从栈中提取出来;
2.如果栈没空&&栈首元素不是我想要的&&A方向来的火车还没有用完->将火车头的那个数字压栈;
3.如果栈没空&&栈首元素不是我想要的&&A方向来的火车用完了->break;
4.如果栈空了&&A方向来的火车没有用完->将火车头的那个数字压栈;
5.如果栈空了&&A方向来的火车用完了->break;
判断驶来的火车是否能够按照指定顺序输出:
1过程执行的次数是否等于车厢节数。
代码部分:
#include <iostream>
#include <stack>
using namespace std;
int main()
{
int a[1001];
int n; cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];//输入"理想队列"("理想编号")
stack<int>st;//队列的定义
int inner = 1, outer = 1;
//innerA方向驶来的车厢编号
//outer 当前应该从B方向出去的车厢的下标编号,
//(这个是"理想编号",根据输入决定的)
int cnt = 0;
while (inner <= n || st.empty() != true)
if (st.empty() != true && a[outer] == st.top())
//如果栈不是空的&&栈顶元素是我想要的
{
cnt++;//在B那头儿贴上一个;
outer++;//查询下一个编号;
st.pop();//因为成功贴上了,栈顶元素就不要了,弹出去;
}
else if (inner <= n)
//else:如果栈为空;else if :如果栈为空&&A方向来的火车车厢还没有用完;
st.push(inner++);
else
//else的含义:
//1.如果栈空了&&火车车厢用完了,那么break;
//2.如果栈没空&&栈手元素不是我想要的&&火车车厢用完了,那么break;
break;
cout << (cnt == n ? "YES" : "NO");
return 0;
}