树上倍增法： LCA问题

树上倍增法用于求解LCA问题是一种非常有效的方法。

倍增是什么？ 简单来说，倍增就是 1 2 4 8 16 … 2^k

可以发现倍增是呈 2的指数型递增的一类数据，和二分一样，二分是缩小范围的，而倍增是扩大的，因此倍增与二分都具有 logn的时间复杂度，对于求解某些问题是非常高效的。

---

什么是树的公共祖先？

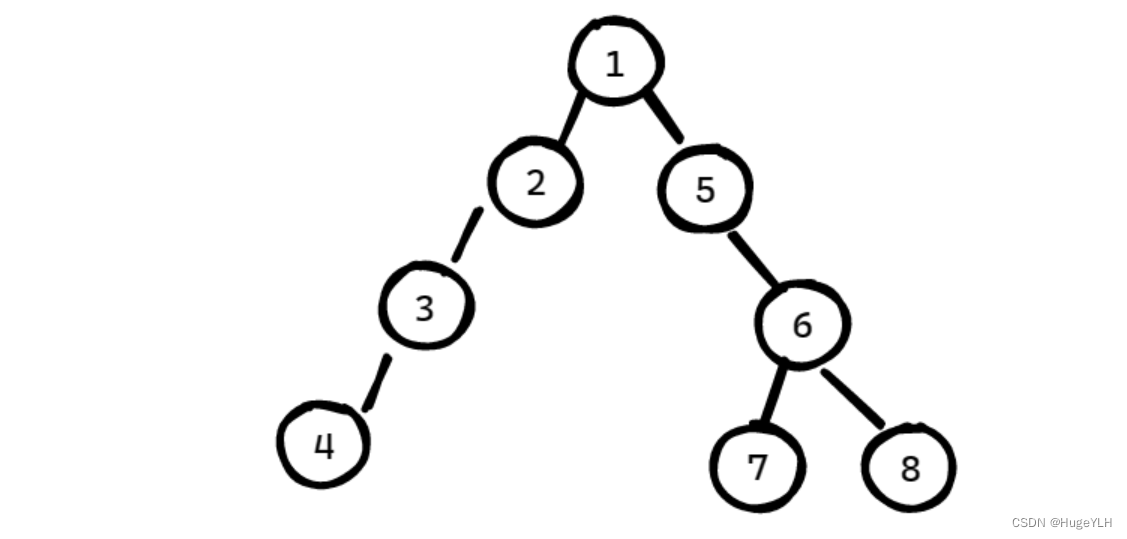
如图所示：

1. 节点 7与 节点8的最近公共祖先是 节点6
2. 节点3 与 节点5的最近公共祖先是节点1

类似这种问题我们可以使用 树上倍增法来实现

---

树上倍增的实现：

首先定义 fa[i] [j] 表示 节点编号为 i 的节点，向根节点方向走了 2^j 步所到达的节点

• 什么是走了 2^j 步？？

走一条边规定为走了一步，j可以表示为 0 ，1，2 ，分别代表走了 1步，2步，4步

走了一步： 到达了节点6

走了两步： 到达了节点5

走了四步：超过了范围，因此只能到达 节点1

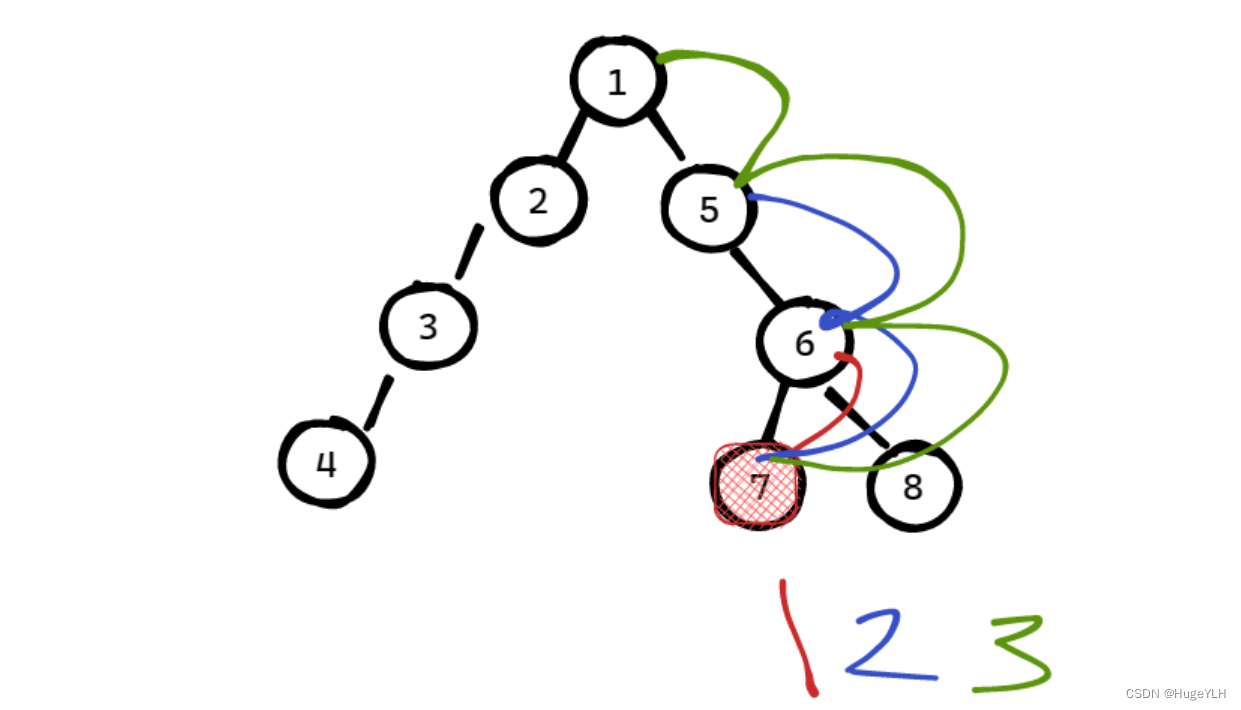
因此我们的 fa数组实际上记录的就是 节点 i 的 第 2^j 个祖先，分别为1：节点6；2：节点5，4：节点1

---

因此首先把整个树结构存储起来（使用链式前向星）

然后首先对整个图进行预处理

• 预处理的目标：

就是把每个 节点的 第 2^j 个的祖先找出来，用于之后的处理，同时我们还需要记录每个节点的深度，我们采用递归的形式，每次递归，节点的深度都是父节点的深度+1

注意：lg数组预处理每个节点的当前深度+1，可以使得某些地方得到优化

void init(int now,int father)
{
    fa[now][0]=father;//第now节点的第2^0个父亲节点，即第一个父亲节点是father
    depth[now]=depth[father]+1;//now的深度是父亲节点深度+1
    //for (int i=1;i<=lg[depth[now]];i++)
    for (int i=1;(1<<i)<=depth[now];i++)
    {
        fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组
    }
    //递归预处理当前点的所有子节点
    for (int i=head[now];i;i=edge[i].next)
    {
        if (edge[i].to!=father)
        {
            init(edge[i].to,now);
        }
    }
}

---

寻找LCA的过程：

我们会发现几个问题：

1. 两个节点的深度不一样，该如何寻找呢？
2. 什么时候寻找结束呢？ 即什么时候才能找到他们的LCA 呢

首先来看第一个问题：

深度不同怎么解决？ x和y节点

• 我们可以假设 x 节点的深度是最大的。
• 每次让x节点往上移动，直到x节点与y节点到达同一深度

什么时候结束寻找？ 即找到了最近公共祖先？

• 当他们位于同一深度的时候，让他们两个节点一起出发，一起往上移动，直到不能再往上移动了为止，他们到达了一个相同的位置，这个节点就是最近公共祖先的节点，返回它即可。

int LCA(int x,int y)
{
    if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度
    while (depth[x]>depth[y])//让x与y到达同一深度，倍增x的深度
    {
        x=fa[x][lg[depth[x]-depth[y]]-1];
    }
    if (x==y) return x;//当他们相同时，LCA就是他们
    for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数，x与y同时倍增，直到xy到达同一位置
    {
        if (fa[x][k]!=fa[y][k])
        {
            x=fa[x][k];
            y=fa[y][k];
        }
    }
    return fa[x][0];//xy到达同一位置，返回父节点
}

---

模板例题：
最近公共祖先

完整AC code

//TODO: Write code here
int n,m,s;
const int N=1e6+10;
int nums[N];
struct Edge
{
    int to,w,next;
}edge[N];
int head[N],cnt;
int fa[N][50],depth[N],lg[N];
void add_edge(int u,int v)
{
    edge[++cnt].next=head[u];
    edge[cnt].to=v;
    head[u]=cnt;
}
void init(int now,int father)
{
    fa[now][0]=father;//第now节点的第2^0个父亲节点，即第一个父亲节点是father
    depth[now]=depth[father]+1;//now的深度是父亲节点深度+1
    for (int i=1;i<=lg[depth[now]];i++)
    {
        fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组
    }
    //递归预处理当前点的所有子节点
    for (int i=head[now];i;i=edge[i].next)
    {
        if (edge[i].to!=father)
        {
            init(edge[i].to,now);
        }
    }
}
int LCA(int x,int y)
{
    if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度
    while (depth[x]>depth[y])//让x与y到达同一深度，倍增x的深度
    {
        x=fa[x][lg[depth[x]-depth[y]]-1];
    }
    if (x==y) return x;//当他们相同时，LCA就是他们
    for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数，x与y同时倍增，直到xy到达同一位置
    {
        if (fa[x][k]!=fa[y][k])
        {
            x=fa[x][k];
            y=fa[y][k];
        }
    }
    return fa[x][0];//xy到达同一位置，返回父节点
}
signed main()
{
	cin>>n>>m>>s;
    for (int i=1;i<=n-1;i++)
    {
        int u,v;
        scanf("%lld%lld",&u,&v);
        add_edge(u,v);
        add_edge(v,u);
    }
    for (int i=1;i<=n;i++)
    {
        lg[i]=lg[i-1]+(1<<lg[i-1]==i);
    }
    init(s,0);
    for (int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%lld%lld",&u,&v);
        printf("%lld\n",LCA(u,v));
    }
#define one 1
	return 0;
}

<<lg[i-1]==i);
}
init(s,0);
for (int i=1;i<=m;i++)
{
int u,v;
scanf(“%lld%lld”,&u,&v);
printf(“%lld\n”,LCA(u,v));
}
#define one 1
return 0;
}

参考：[树上倍增法](https://blog.csdn.net/chengqiuming/article/details/126694822)