作者：指针不指南吗
专栏：算法篇

🐾或许会很慢，但是不可以停下🐾

一、快速排序 ( Quick Sort )

1.思路

• 找出一个分界点，随机的
• 调整区间
  分治，双指针，指向两边，往中间走，遇到不满足条件的停下，直到两者都遇到不满足条件的，交换位置，直到两个指针相遇
• 递归处理两段

分治
三步曲：分成子问题，解决子问题，子问题合并成大问题

---

---

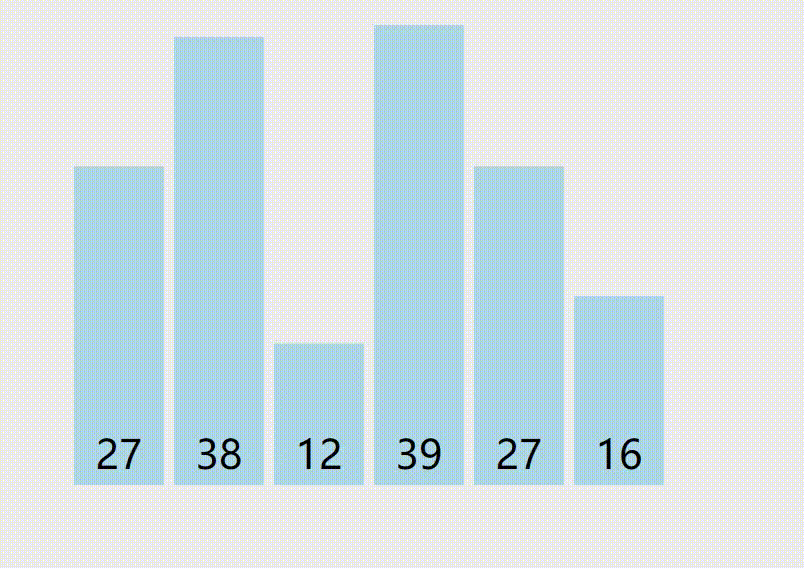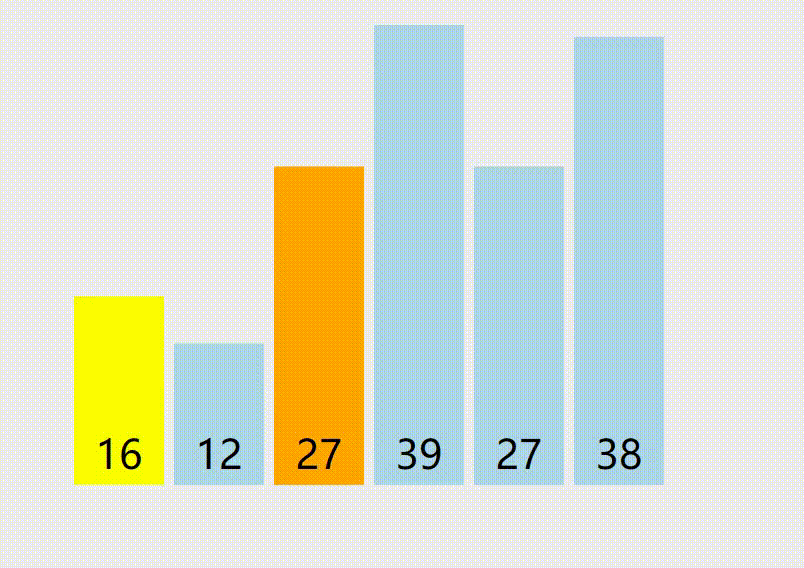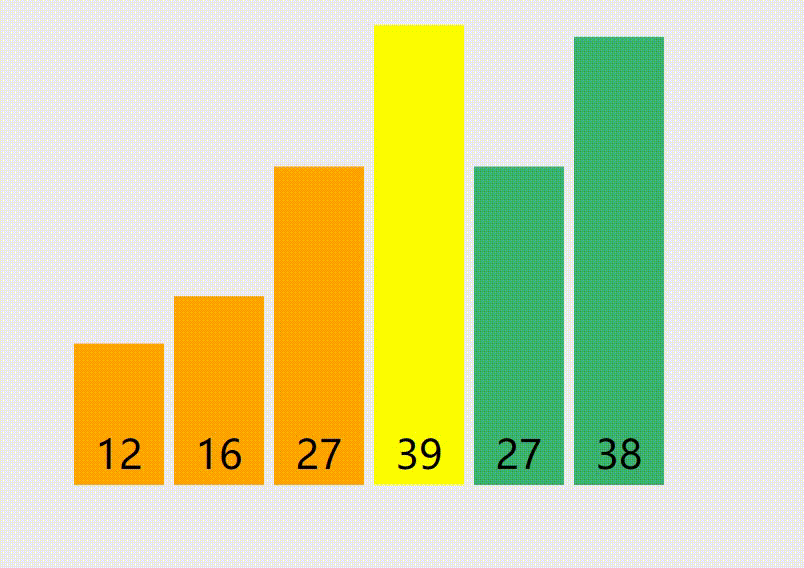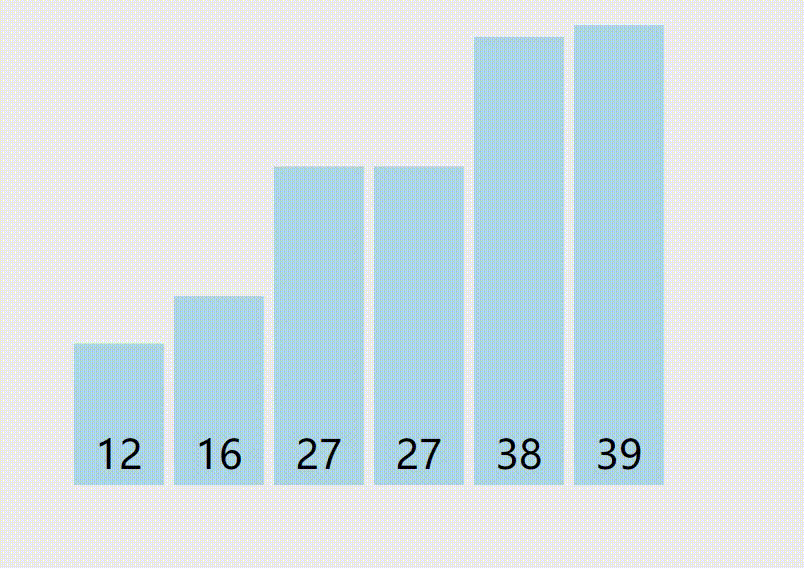
2. 代码模板

void quick_sort (int q [ ] , int l , int r )
{
	if (l>= r) return ; //区间个数为 1，或者 0，返回
	
	int i =l-1;j=r+1;x=q[l+r>>1];  // i指左边, j指最右边,范围大点，要包含 l , r  
	
	while(i<=j){
		do i++;while(q[i]>x);  //指针移动，直到出现不满足条件的情况
		do j--;while(q[j]<x);
		if(i<j)  swap(q[i],q[j];   //找到 2个，交换
		}
		
	quick_sort(q,l,j),quick_sort(q,j+1,r);  //递归
	}

---

---

二、归并排序 ( Merge Sort )

1.思路

• 确定一个分界点
• 递归排序
• 合二为一
  分成两组数据，然后两组数据从最小的比较，谁小放在temp数组，，其中一组数据已经走完了，另一组还剩着，把剩余的放在temp数组后面，最后temp 赋值给 q 即原始数组

---

---

2.代码模板

void merge_sort(int q[],int l,int r)
{
	if(l>=r) return ;  //区间只有一个元素或没有，返回 
	int mid=l+r>>1;    //确定中间值 
	
	merge_sort(q,l,mid),merge_sort(q,mid+1,r);   //递归排序 
	
	int i=l,j=mid+1,k=0;
	while(i<=mid&&j<=r){
		if(q[i]<=q[j]) temp[k++]=q[i++];  //谁小，谁就先存储在temp中 
		else temp[k++]=q[j++];
	}
	
	while(i<=mid) temp[k++]=q[i++];   //谁有剩余即其数大，存储在temp后面 
	while(j<=r) temp[k++]=q[j++];
	
	for(int i=l,j=0;i<=r;i++,j++) q[i]=temp[j];  //拷贝到原数组 
}

总结

快排和归并排序💭

• 思路上

快排是先处理两边，再递归
归并是先递归，在处理两边

• 时间复杂度上

快排 和 归并排序 的时间复杂度都是 O($lo{g}_{2}n$ )

• 快排平均 O($lo{g}_{2}n$ )，最坏情况可以达到 O($n^2$)
• 归并排序的最坏和最好情况都是 O($lo{g}_{2}n$ )