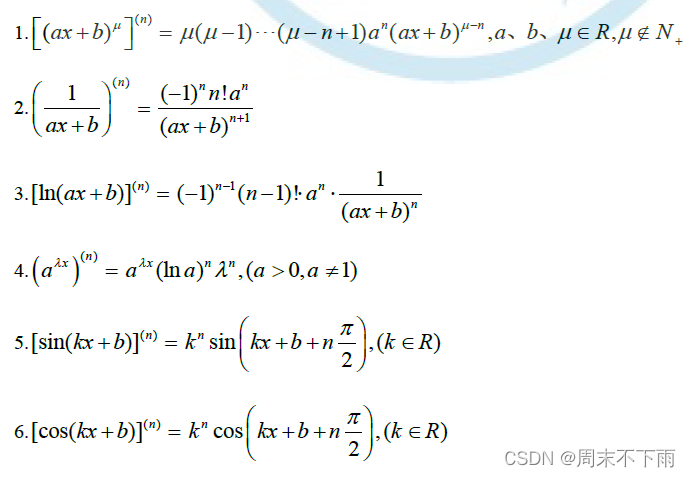文章目录

• 一、基础概念定理部分
• • 1.1 导数的四则运算法则
  • 1.2 反函数的求导法则
  • 1.3 复合函数的求导法则
  • 1.4 费马引理
  • 1.5 罗尔定理
  • 1.6 拉格朗日中值定理
  • 1.7 导数为零的结论
  • 1.8 柯西中值定理
  • 1.9 洛必达法则
  • 1.10 泰勒中值定理（定理1，定理2）
  • 1.11 导数判断函数的单调性（定理1）
  • 1.12 导数判断函数的凹凸性（定理2）
  • 1.13 极值的第2充分条件（定理3）
  • 1.14 曲率公式的证明
• 二、基本公式
• • 2.1 导数定义与常见函数导数
  • 2.2 莱布尼茨公式
  • 2.3 高阶导数常用公式