目录
- 1. 聚类原理
- 1.1. 无监督与聚类
- 1.2. K均值算法
- 2. 公式推导
- 2.1. 距离
- 2.2. 最小平方误差
- 3. 实例
- 3.1. python实现
- 3.2. sklearn实现
- 4. 运行(可直接食用)
1. 聚类原理
1.1. 无监督与聚类
在这部分我今天主要介绍K均值聚类算法,在这之前我想提一下“无监督学习”和“聚类”。
无监督学习是指训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质和规律的学习。
在 sklearn 官网首页中,非常贴心的将任务分为了分类,回归,聚类三类,以此我们可以看出聚类的重要性。实际上聚类就是把训练集中的样本划分为通常不相交的几个子集,每个子集称为一个簇,每个簇对应的名字聚类事先是不知道的,需要靠使用者来把握命名。
优点
简单有效
缺点
对于K均值算法来说,最明显的缺点有很多:一开始定中心点数量需要人为定;中心点选取初始样本是随机选的。很多K均值优化算法都是从这几个方面入手改进的。
1.2. K均值算法
对于K均值算法,西瓜书的伪代码其实已经说的很明白了:

简单的说就是三步:
- 选择初始中心点,最基本的方法是从数据集中选择样本。初始化后,K-means由其他两个步骤之间的循环组成。
- 将每个样本指定给其最近的中心。
- 通过获取分配给每个先前中心的所有样本的平均值来创建新的中心。计算新旧质心之间的差值,算法重复最后两个步骤,直到该值小于阈值。
一般来说,中心点不会是已经存在的点,一般都是算出来的虚构的点。
提一下 对于高维数据,我们知道存在维度诅咒这一说法,所以在很多时候聚类往往会跟PCA之类的降维算法搭配。在降维算法中 TSNE 因为能将数据降维至2-3维,非常适合可视化,而且降维效率也高,所以也很常用。
2. 公式推导
2.1. 距离
简单的说,对于每个簇来说,簇内相似度高,簇外相似度低(高内距,低耦合)。那么衡量距离的方法有哪些?
- 曼哈顿距离
- 欧式距离
- 闵可夫斯基距离 d i s t m k ( x i , x j ) = ( ∑ u = 1 n ∣ x i u − x j u ∣ p ) 1 p dist_mk(x_i,x_j)=(\sum_{u=1}^n|{x_{iu}-x_{ju}|^p})^{\frac{1}{p}} distmk(xi,xj)=(∑u=1n∣xiu−xju∣p)p1
- 余弦相似度 c o s ( θ ) = ∑ i = 1 n ( x i × y i ) ∑ i = 1 n ( x i ) 2 × ∑ i = 1 n ( y i ) 2 cos(\theta)=\frac{\sum_{i=1}^n(x_i\times y_i)}{\sqrt{\sum^n_{i=1}{(x_i)^2}} \times \sqrt{\sum^n_{i=1}{(y_i)^2}}} cos(θ)=∑i=1n(xi)2×∑i=1n(yi)2∑i=1n(xi×yi)
- 等等
注:p=1,闵可夫斯基距离为曼哈顿距离;p=2,闵可夫斯基距离为欧氏距离。
2.2. 最小平方误差
说白了就是每个簇内每个点到中心点的距离的和最小。
E
=
∑
i
=
1
k
∑
x
∈
C
i
∣
∣
x
−
μ
i
∣
∣
2
2
E = \sum^k_{i=1}{\sum_{x\in C_i}{||x-\mu_i||_2^2}}
E=i=1∑kx∈Ci∑∣∣x−μi∣∣22
μ
i
\mu_i
μi就是中心点,数学公式表示就是
μ
i
=
1
∣
C
i
∣
∑
x
∈
C
i
x
\mu_i=\frac{1}{|C_i|}\sum_{x\in C_i}{x}
μi=∣Ci∣1x∈Ci∑x
3. 实例
西瓜数据集4.0为例
密度,含糖率
0.697,0.46
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.36,0.37
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459
3.1. python实现
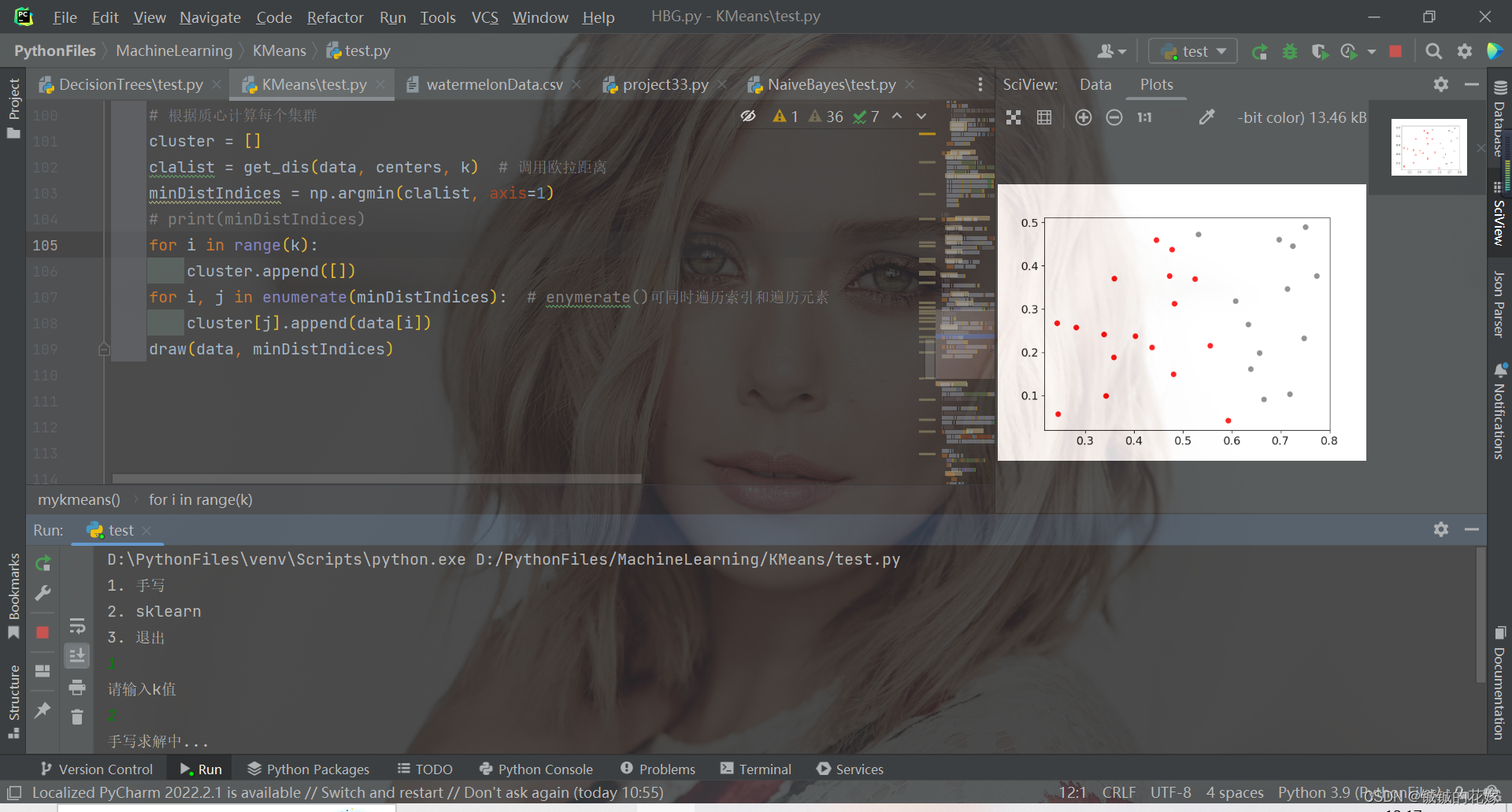
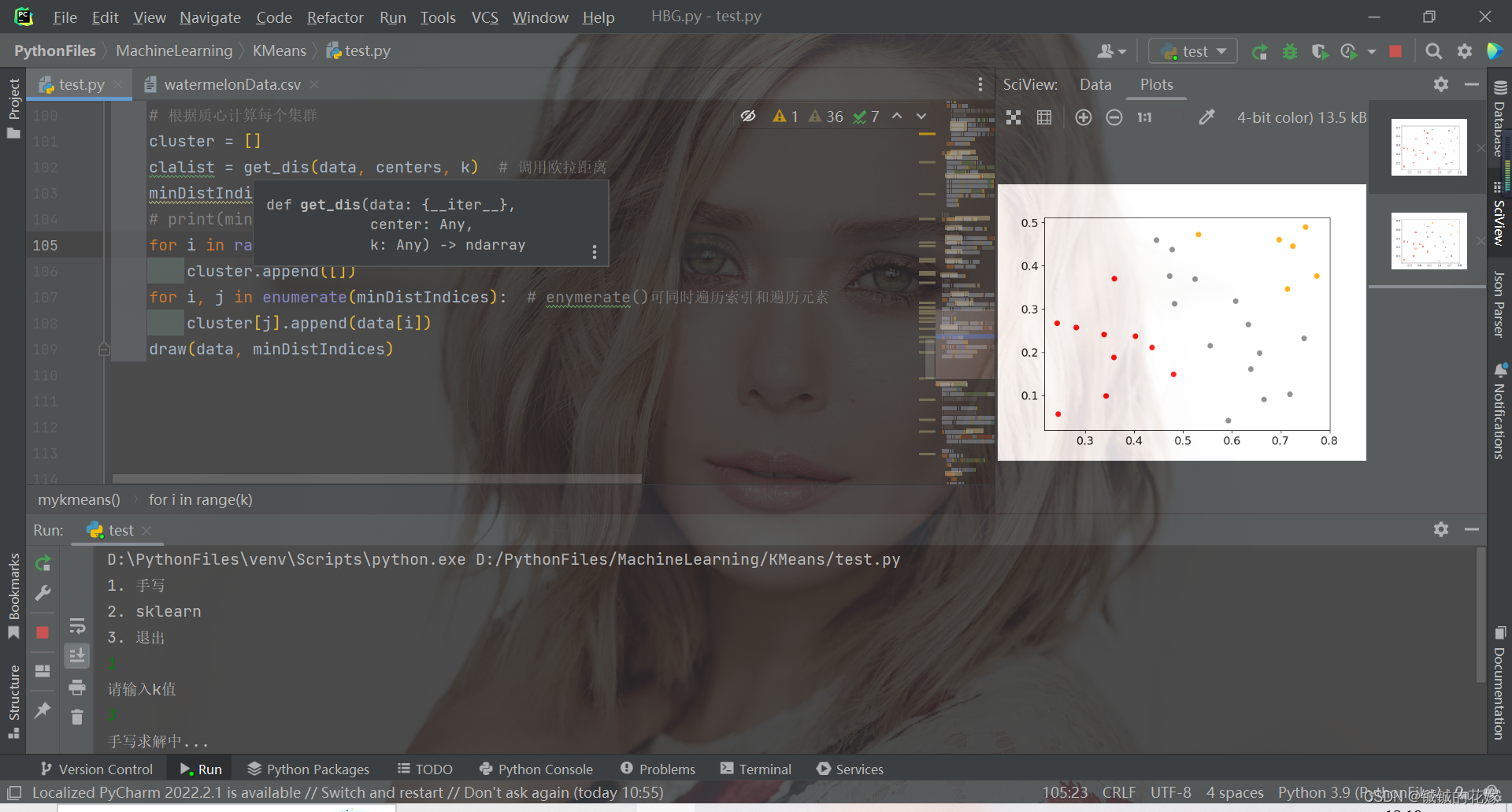
def mykmeans(data, k):
# 计算距离
def get_dis(data, center, k):
ret = []
for point in data:
# np.tile(a, (2, 1))就是把a先沿x轴复制1倍,即没有复制,仍然是[0, 1, 2]。 再把结果沿y方向复制2倍得到array([[0, 1, 2], [0, 1, 2]])
# k个中心点,所以有k行
diff = np.tile(point, (k, 1)) - center
squaredDiff = diff ** 2 # 平方
squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)
distance = squaredDist ** 0.5 # 开根号
ret.append(distance)
return np.array(ret)
def draw(data, cluster):
D_data = pd.DataFrame(data)
plt.rcParams["font.size"] = 14
colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])
D_data["cluster"] = cluster
D_data = D_data.sort_values(by="cluster")
xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化
yy = np.array(D_data[D_data.columns[1]])
cc = np.array(D_data["cluster"])
plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]
plt.show()
plt.close()
# 计算质心
def classify(data, center, k):
# 计算样本到质心的距离
clalist = get_dis(data, center, k)
# 分组并计算新的质心
minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标
newCenter = pd.DataFrame(data).groupby(
minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值
newCenter = newCenter.values
# 计算变化量
changed = newCenter - center
return changed, newCenter
data = data.tolist()
# 随机取质心
centers = random.sample(data, k)
# 更新质心 直到变化量全为0
changed, newCenters = classify(data, centers, k)
while np.any(changed != 0):
changed, newCenters = classify(data, newCenters, k)
centers = sorted(newCenters.tolist()) # tolist()将矩阵转换成列表 sorted()排序
# 根据质心计算每个集群
cluster = []
clalist = get_dis(data, centers, k) # 调用欧拉距离
minDistIndices = np.argmin(clalist, axis=1)
print(minDistIndices)
for i in range(k):
cluster.append([])
for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素
cluster[j].append(data[i])
draw(data, minDistIndices)
3.2. sklearn实现
def sk(data, k):
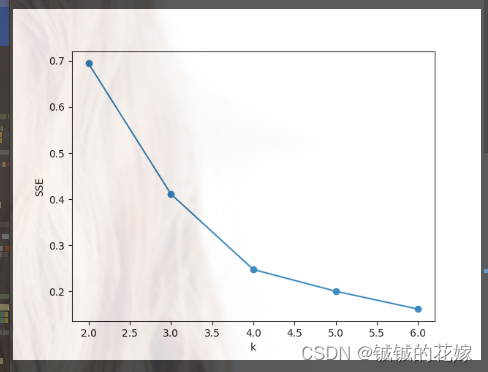
# # 肘部法取k值
# data = np.array(data)
# SSE = []
# right = min(7, data.shape[0])
# for k in range(2, right):
# km = KMeans(n_clusters=k)
# km.fit(data)
# SSE.append(km.inertia_)
# xx = range(2, right)
# plt.xlabel("k")
# plt.ylabel("SSE")
# plt.plot(xx, SSE, "o-")
# plt.show()
D_data = pd.DataFrame(data)
km = KMeans(n_clusters=k).fit(data)
# print(km.labels_)
print("质心")
center = km.cluster_centers_
print(center)
D_data["cluster"] = km.labels_
plt.rcParams["font.size"] = 14
colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])
D_data["cluster"] = km.labels_
D_data = D_data.sort_values(by="cluster")
xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化
yy = np.array(D_data[D_data.columns[1]])
cc = np.array(D_data["cluster"])
plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]
if D_data.shape[0] >= 1:
plt.scatter(center[:, 0], center[:, 1], marker="o", s=15, c="black") # 画中心点
plt.show()
plt.close()
4. 运行(可直接食用)
import random
from collections import Counter
import numpy as np
import pandas as pd
import warnings
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
from sklearn.manifold import TSNE
warnings.filterwarnings("ignore")
def sk(data, k):
# # 肘部法取k值
# data = np.array(data)
# SSE = []
# right = min(7, data.shape[0])
# for k in range(2, right):
# km = KMeans(n_clusters=k)
# km.fit(data)
# SSE.append(km.inertia_)
# xx = range(2, right)
# plt.xlabel("k")
# plt.ylabel("SSE")
# plt.plot(xx, SSE, "o-")
# plt.show()
D_data = pd.DataFrame(data)
km = KMeans(n_clusters=k).fit(data)
# print(km.labels_)
print("质心")
center = km.cluster_centers_
print(center)
D_data["cluster"] = km.labels_
plt.rcParams["font.size"] = 14
colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])
D_data["cluster"] = km.labels_
D_data = D_data.sort_values(by="cluster")
xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化
yy = np.array(D_data[D_data.columns[1]])
cc = np.array(D_data["cluster"])
plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]
if D_data.shape[0] >= 1:
plt.scatter(center[:, 0], center[:, 1], marker="o", s=15, c="black") # 画中心点
plt.show()
plt.close()
def mykmeans(data, k):
# 计算距离
def get_dis(data, center, k):
ret = []
for point in data:
# np.tile(a, (2, 1))就是把a先沿x轴复制1倍,即没有复制,仍然是[0, 1, 2]。 再把结果沿y方向复制2倍得到array([[0, 1, 2], [0, 1, 2]])
# k个中心点,所以有k行
diff = np.tile(point, (k, 1)) - center
squaredDiff = diff ** 2 # 平方
squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)
distance = squaredDist ** 0.5 # 开根号
ret.append(distance)
return np.array(ret)
def draw(data, cluster):
D_data = pd.DataFrame(data)
plt.rcParams["font.size"] = 14
colors = np.array(["red", "gray", "orange", "pink", "blue", "green"])
D_data["cluster"] = cluster
D_data = D_data.sort_values(by="cluster")
xx = np.array(D_data[D_data.columns[0]]) # 取前两个维度可视化
yy = np.array(D_data[D_data.columns[1]])
cc = np.array(D_data["cluster"])
plt.scatter(xx, yy, c=colors[cc]) # c=colors[cc]
plt.show()
plt.close()
# 计算质心
def classify(data, center, k):
# 计算样本到质心的距离
clalist = get_dis(data, center, k)
# 分组并计算新的质心
minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标
newCenter = pd.DataFrame(data).groupby(
minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值
newCenter = newCenter.values
# 计算变化量
changed = newCenter - center
return changed, newCenter
data = data.tolist()
# 随机取质心
centers = random.sample(data, k)
# 更新质心 直到变化量全为0
changed, newCenters = classify(data, centers, k)
while np.any(changed != 0):
changed, newCenters = classify(data, newCenters, k)
centers = sorted(newCenters.tolist()) # tolist()将矩阵转换成列表 sorted()排序
# 根据质心计算每个集群
cluster = []
clalist = get_dis(data, centers, k) # 调用欧拉距离
minDistIndices = np.argmin(clalist, axis=1)
# print(minDistIndices)
for i in range(k):
cluster.append([])
for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素
cluster[j].append(data[i])
draw(data, minDistIndices)
if __name__ == '__main__':
random.seed(1129)
data = pd.read_csv("watermelonData.csv").sample(frac=1, random_state=1129)
# 因为西瓜数据集每列都是0到1的,所以这里就不进行标准化了
data_shuffled = np.array(data)
# 划分训练集测试集,感觉不太需要测试集,直接把比例拉到1
data_train = data_shuffled[:int(data_shuffled.shape[0]*1), :]
data_test = data_shuffled[data_train.shape[0]:, :]
# 维度上去了就降维
if data_train.shape[1]>10:
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000, method='exact', random_state=0)
data_train = tsne.fit_transform(data_train)
choice = 0
while choice != 3:
print("1. 手写\n2. sklearn\n3. 退出")
try:
choice = int(input())
except:
break
if choice == 1:
print("请输入k值")
try:
k = int(input())
except:
break
print("手写求解中...")
# 参考:https://blog.csdn.net/qq_43741312/article/details/97128745
# 主要是发现了很多np和pd在计算的时候的用法
mykmeans(data_train, k)
elif choice == 2:
print("请输入k值")
try:
k = int(input())
except:
break
print('sklearn yyds')
sk(data_train, k)
else:
print("退出成功")
choice = 3
break
参考:
吴恩达《机器学习》
sklearn官网
《百面机器学习》