文章目录
- 前置概念
- 一、构造平衡二叉树的基本思想
- 二、一个示例
- 三、平衡二叉树的调整细节
- (1)LL型(顺时针 )
- 举例
- (2)RR型(逆时针)
- (3)LR型(先逆时针再顺时针)
- 举例
- (4)RL型(先顺时针再逆时针)
- (5)四种调整类型总结
- 四、例题
- 解题过程
参考视频:
懒猫老师-数据结构-(59)平衡二叉树【互动视频】
前置概念
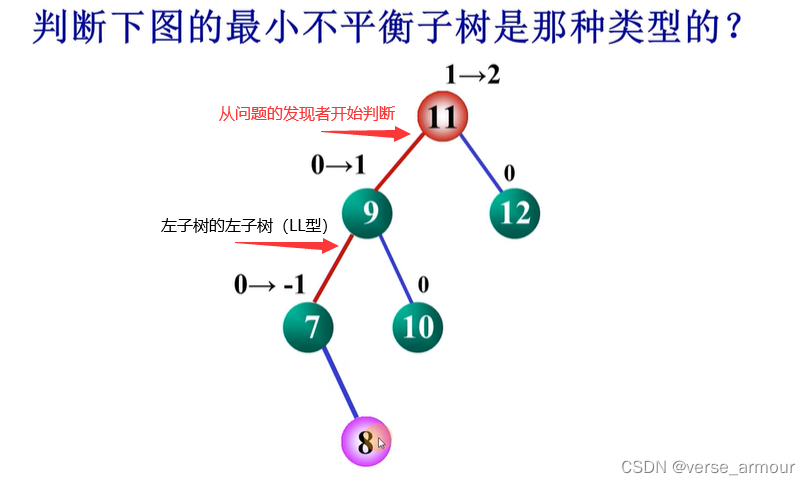
最小不平衡子树:在平衡二叉树的构造过程中,以
距离插入结点最近的、且平衡因子的绝对值大于1的结点为根的子树。
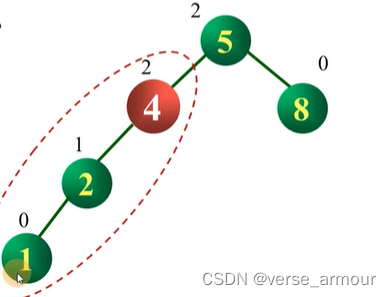
例如上图,此处4就是最小不平衡子树的根节点。
一、构造平衡二叉树的基本思想
每插入一个结点,
- 从插入结点向上计算各结点的平衡因子,如果某结点的平衡因子的绝对值大于1,则说明插入操作破坏了二叉排序树的平衡性,需要进行平衡调整;否则继续执行插入操作。
- 如果二叉排序树不平衡,则找出最小不平衡子树的根节点,根据新插入结点与最小不平衡子树根节点的关系判断调整类型。
- 根据调整类型进行相应的调整,使之成为新的平衡子树。
二、一个示例
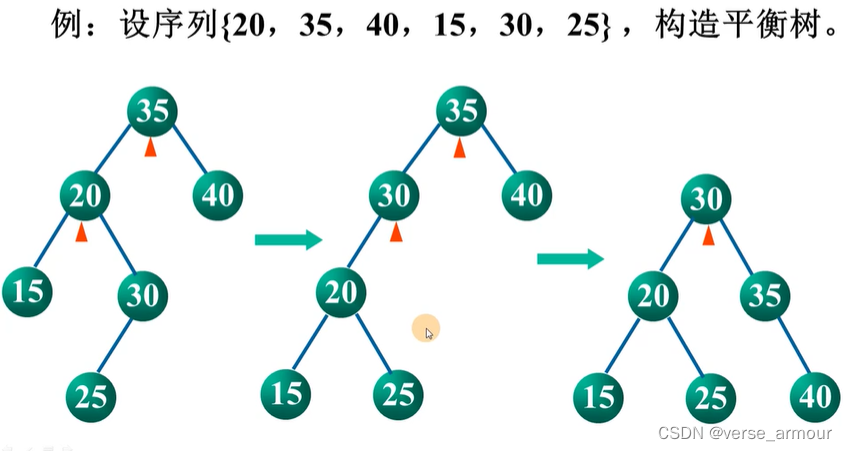
三、平衡二叉树的调整细节
设结点A为最小不平衡子树的根结点,对该子树平衡调整有以下四种情况:
- LL型
- RR型
- LR型
- RL型
(1)LL型(顺时针 )
插入结点X之后,这棵二叉树不平衡了。B结点的平衡因子变成1(h+1-h),A结点的平衡因子变成2(h+2-h)。这里我们称X结点为问题的发生者;A结点为问题的发现者。从问题的发现者A结点到问题的发生者要经过左子树的左子树(即LL)。
现在A发现二叉树不平衡了,就需要对二叉树进行调整。
旋转:扁担原理; 冲突:旋转优先
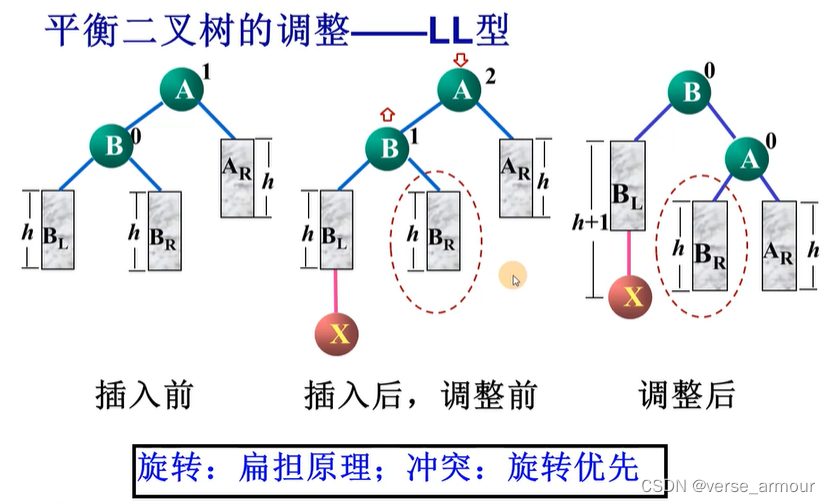
利用扁担原理,A结点的左右子树不平衡了:左子树“重”,右子树“轻”。那么我们把B结点往上抬,A结点往下压(进行了一个顺时针旋转),A结点变成了B结点的右子树,B结点原来的右子树调整为A结点的左子树(B结点的右子树上的所有结点一定小于A结点,所以将B原来的右子树调整为A结点的左子树是最合适的)。
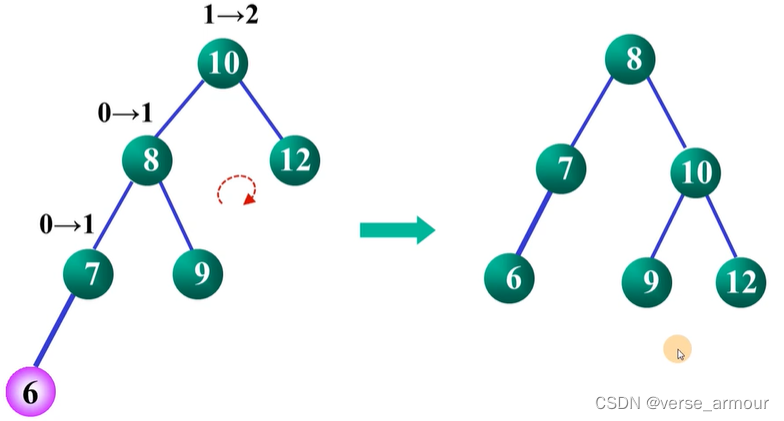
举例
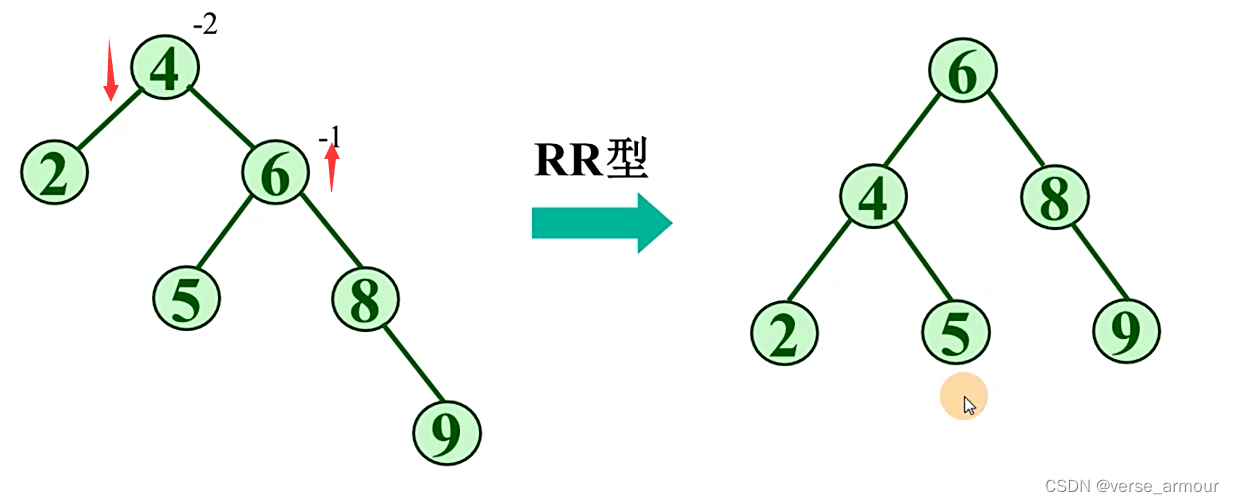
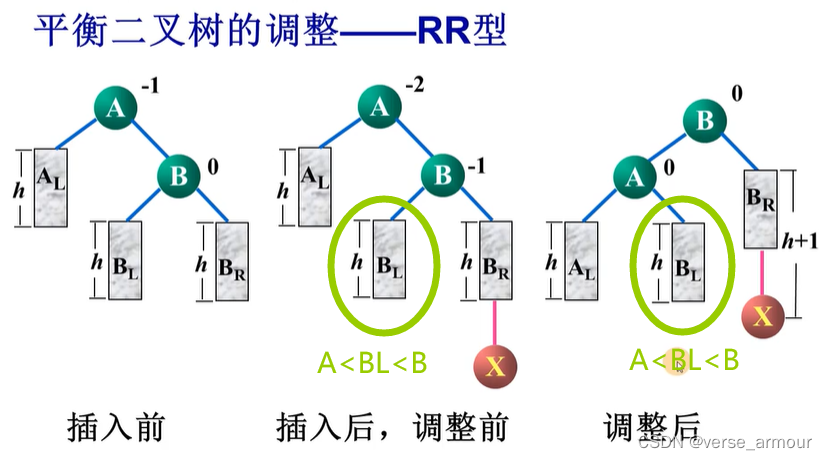
(2)RR型(逆时针)
(3)LR型(先逆时针再顺时针)
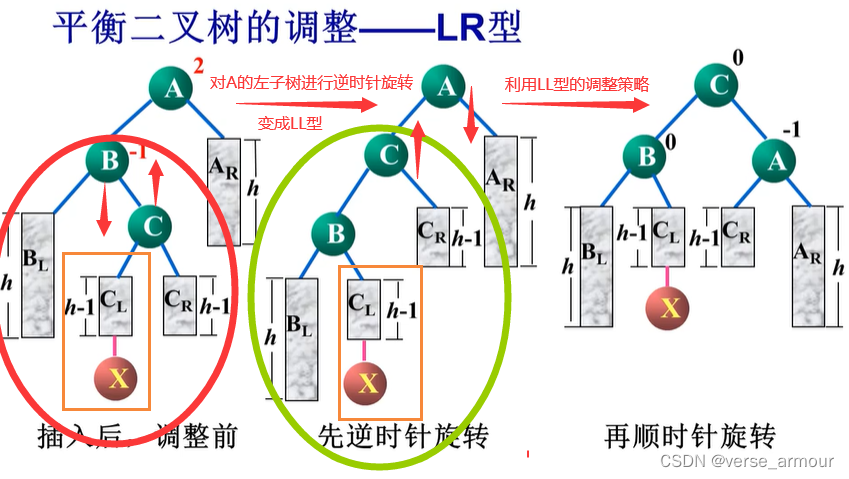
理解记忆:想象我们正在背一个扁担,发现左边重,但对于左边来说,左边的右边又比较重,所以这个LR型调整成平衡二叉树更为复杂。我们先需要对左边好好调整一番,规整一下(逆时针旋转),调整成LL型,让所有重量完全彻底地压到左边。接着对得到的LL型一次性向右调整(顺时针旋转)。
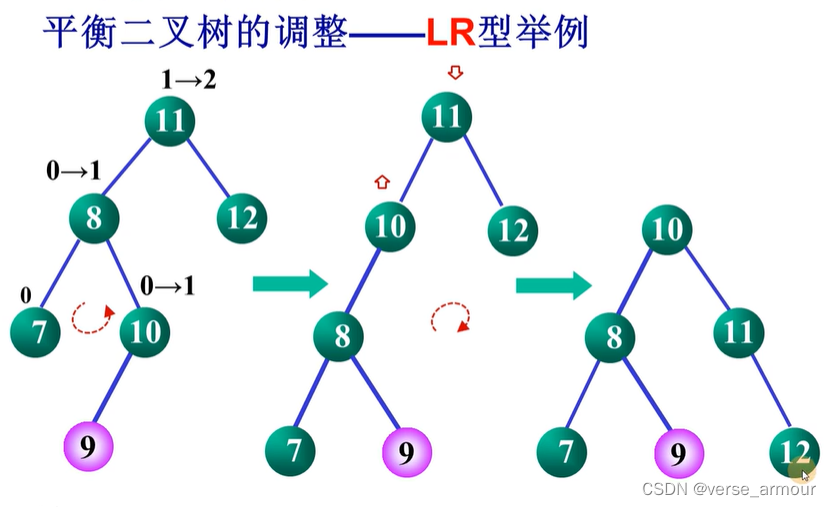
举例
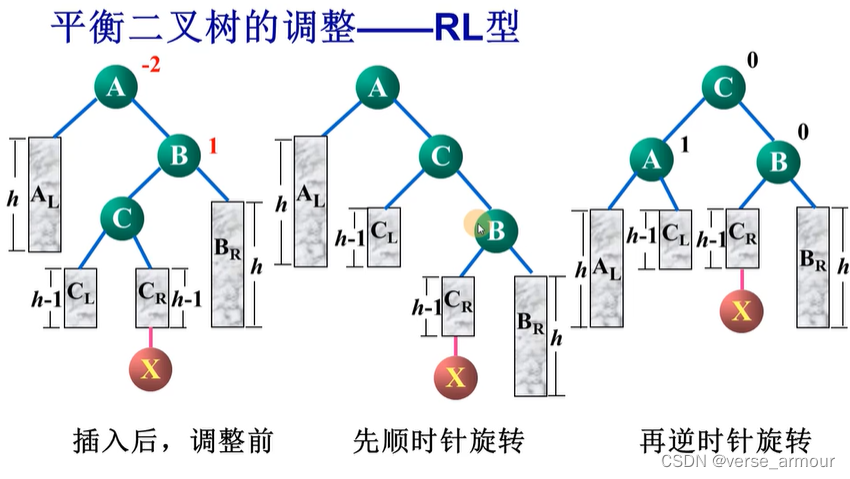
(4)RL型(先顺时针再逆时针)
(5)四种调整类型总结

四、例题
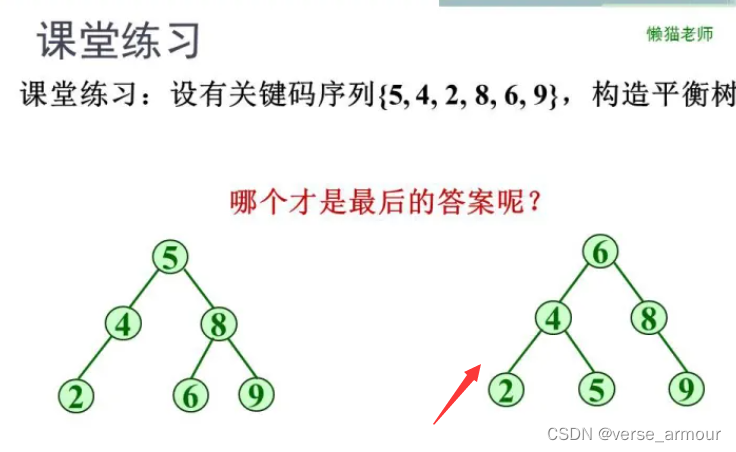
解题过程
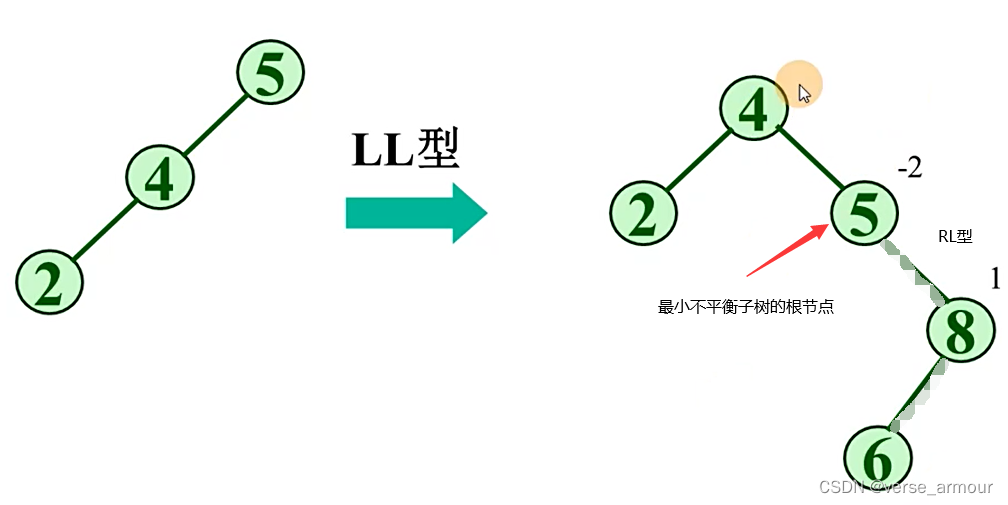
-
找到最小不平衡子树的根结点:5
-
判断类型:从问题的发现者开始到问题的发生者,先左后右,画圈的为RL型不平衡树。
注意:下面对画圈的部分独立操作。 -
将RL型的不平衡树进行顺时针旋转变成RR型
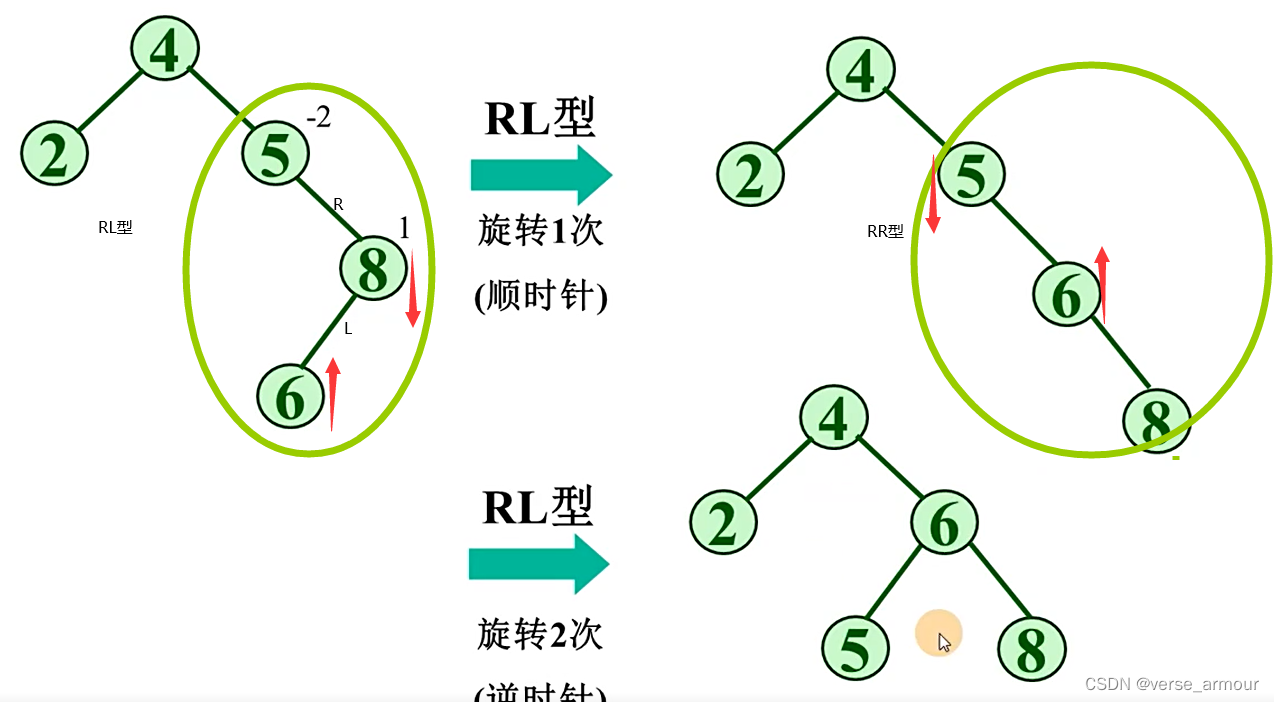
-
插入结点9,发现二叉树又不平衡了,找到最小不平衡子树的根结点:4
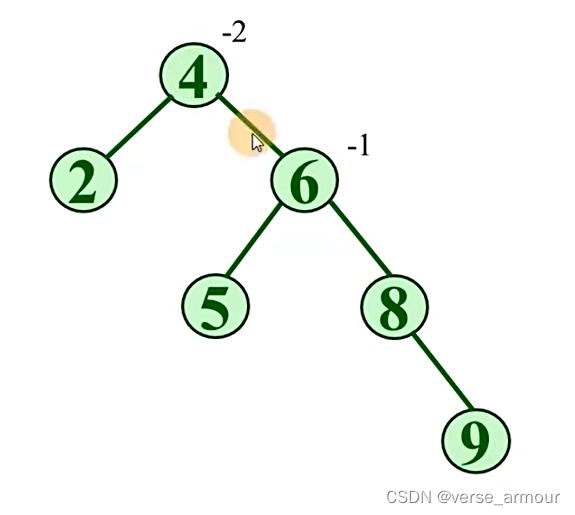
- 判断类型:RR型不平衡树
- 对RR型不平衡树进行逆时针旋转