2017国赛
题目描述
小明的实验室有 N 台电脑,编号1⋯N。原本这 N 台电脑之间有 N−1 条数据链接相连,恰好构成一个树形网络。在树形网络上,任意两台电脑之间有唯一的路径相连。
不过在最近一次维护网络时,管理员误操作使得某两台电脑之间增加了一条数据链接,于是网络中出现了环路。环路上的电脑由于两两之间不再是只有一条路径,使得这些电脑上的数据传输出现了 BUG。
为了恢复正常传输。小明需要找到所有在环路上的电脑,你能帮助他吗?
输入描述
输入范围:
第一行包含一个整数 N 。
以下 N 行每行两个整数 a,b,表示 a 和 b 之间有一条数据链接相连。
其中, 1≤N≤10^5,1≤a,b≤N。
输入保证合法。
输出描述
按从小到大的顺序输出在环路上的电脑的编号,中间由一个空格分隔。
输入输出样例
输入
5 1 2 3 1 2 4 2 5 5 3输出
1 2 3 5
题目大意
有一个树,N个节点,编号l-N树中多了一条边,导致了环的产生找出所有环上的节点,按升序输出
树是一种特殊的图](无环图)
一个N个节点的树,边数是N-1
解题思路:拓扑排序
知识补充1:节点的入度和出度
- 节点的入度:从别处进入该节点的边数,例如下图结点3的入度为2.
- 节点的出度:从该节点出去的边数,例如下图结点1的出度为2.
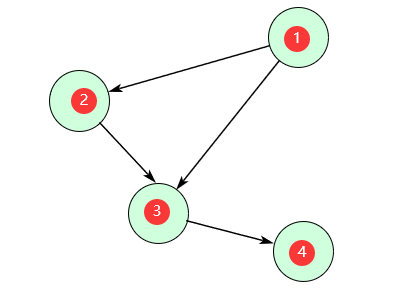
题目给的是无向图,无向图是一种特殊的有向图,每一条边都是双向的。
知识补充2:邻接表存储树/图
邻接表(本质是一个二维列表),为每个节点建立一个链表(list就可以)
每个节点对应的链表存储它可到达的相邻节点
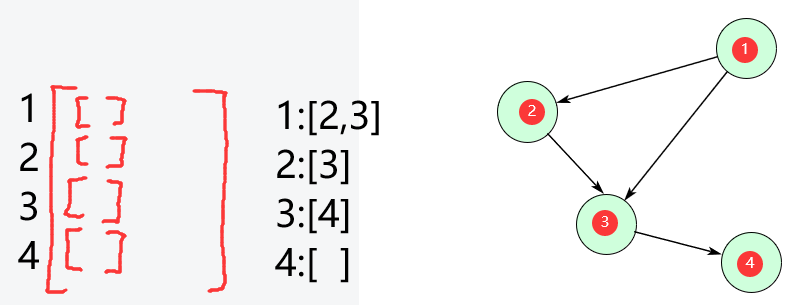
若是无向图,则邻接表为:

拓扑排序
本题可用DFS实现,也可用BFS实现
用邻接表的形式存储这个多了一条边的树,同时记录每个节点的入度(用一个列表d)
对所有入度是1的节点进行搜索,搜索过程中,它们搜索到的相邻节点入度减1,如果更新后的入度是1,继续搜索,否则结束搜索。
【图解BFS】:首先对所有入度是1的节点(下图橙色的点)进行搜索,搜索节点1和2后,节点5的入度为3-1-1=1。搜索节点3后,节点6的入度为,3-1=2,搜索节点4后,节点7的入度为3-1=2。继续搜索,发现入度为1的点只有节点5,搜索节点5后,节点8的入度为3-1=2。至此,没有入度为1的节点,结束搜索。发现没有搜索到的节点刚好连成一个环,就是题目要求的结果。

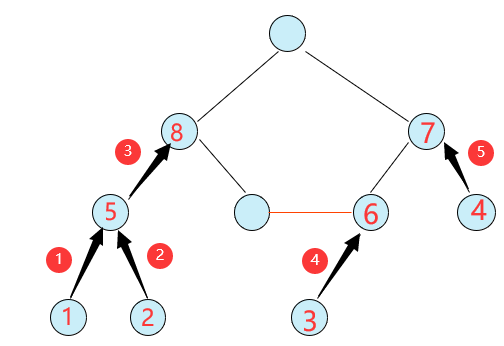
【图解DFS】 (红圈序号代表搜索顺序) 首先对节点1搜索,节点5的入度3-1=2,停止搜索;对节点2搜索,节点5入度2-1=1,继续搜索结点5,结点8的入度3-1=2,停止搜索;对节点3继续搜索,节点6的入度3-1=2,停止搜索;对节点4进行搜索,节点7的入度3-1=2,停止搜索。
vis[ ]数组对所有搜索过的点打标记,最后统计,没有被标记过的节点一定在环上。(因为只是搜索入度为1的点,而环上的点入度至少为2,因此环上的点不会被搜索到)
代码1:BFS+拓扑排序
from collections import deque
n = int(input())
g = [[] for _ in range(n + 1)] # 邻接表(n+_1是因为第一行第一列用0占位,从下标1开始)
d = [0] * (n + 1)
vis = [0] * (n + 1) # vis[ ]数组对所有搜索过的点打标记,最后统计,没有被标记过的节点一定在环上
def topsort(): # 拓扑排序
q = deque()
for i in range(1, n + 1): # 遍历所有节点
if d[i] == 1: # 搜索入度为1
q.append(i) # 入队
vis[i] = 1 # 标记为搜索过
while len(q):
c = q.popleft() # 取出队头
for i in g[c]: # 搜索相邻节点
d[i] -= 1 # 每次搜索,入度-1
if d[i] == 1: # 如果相邻节点入度为1
q.append(i) # 入队
vis[i] = 1 # 标记为搜索过
for i in range(1, n + 1):
a, b = map(int, input().split()) # 读入连接关系
g[a].append(b) # 创建关系:列表a存入b
g[b].append(a) # 创建关系:列表b存入a
d[a] += 1 # a的入度+1
d[b] += 1 # b的入度+1
topsort()
ring = [] # 用来存环
for i in range(1, n + 1):
if not vis[i]: # 找到没有标记过的
ring.append(i) # 加到环上
ring.sort() # 从小到大排序
print(*ring) # 将列表元素逐个输出代码2:DFS+拓扑排序
n = int(input())
g = [[] for _ in range(n + 1)]
d = [0] * (n + 1)
vis = [0] * (n + 1)
def dfs(c):
vis[c] = 1 # 标记为搜索过
for i in g[c]: # 搜索相邻节点
d[i] -= 1 # 入度-1
if d[i] == 1:
dfs(i)
def topsort():
for i in range(1, n + 1):
if d[i] == 1: # 搜索入度为1的节点
dfs(i)
for i in range(1, n + 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
d[a] += 1
d[b] += 1
topsort()
ring = []
for i in range(1, n + 1):
if not vis[i]:
ring.append(i)
ring.sort()
print(*ring)代码3:直接DFS (比较难想到)
N = int(input())
edge = [[] for i in range(N+1)] #邻接表,0不用
pre = [0] * (N+1) #前驱点,用于生成环
ring = [] #记录环
vis = [False] * (N+1) #vis[i]=True表示这个点已经访问过
for i in range(N):
u, v = map(int, input().split())
edge[u].append(v) #记录连接关系
edge[v].append(u)
def dfs(x,fa): #x和它的父亲fa
vis[x] = True #将当前节点标记为已访问
for son in edge[x]: #寻找连接的节点
if len(ring) > 0: return #这点已经确定在环上,不找了
if not vis[son]: #son未被标记,递归找
pre[son] = x #son的前驱记录为x
dfs(son, x) #son是从x找过来的
elif son != fa: #son已被标记,而且不是从x走过来的(当前节点存在两个入度)
tmp = x #发现了环,son是环的终点,x是son的前继
while tmp != son: #不断向前寻找,向环中添加节点
ring.append(tmp)
tmp = pre[tmp]
ring.append(son) #把环的终点加入
dfs(1, 0)
ring.sort() #排序使其从小到大
for k in ring: print(k, end=' ')