目录
一、图的基本概念
二、图的存储
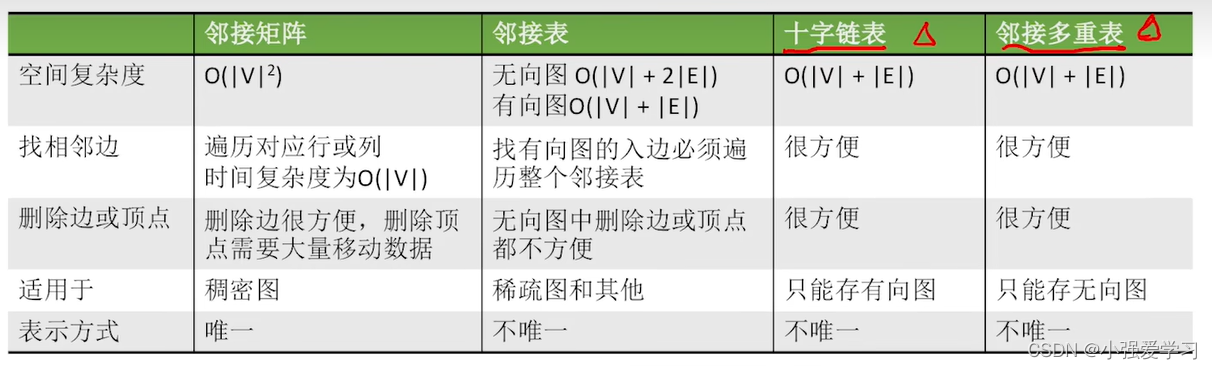
1、邻接矩阵法
2、邻接表法(顺序+链式存储)
3、十字链表存储
4、邻接多重表
三、图的基本操作
四、图的遍历
1、广度优先遍历
2、深度优先遍历
一、图的基本概念

1、图的定义

2、无向图
- 若E是无向边 简称边) 的有限集合时,则图G为无向图。边真是顶点的无序对,记为(v,w)或(w,v),因为(v,w)=(w,v),其中v、w是顶点。可以说顶点w和顶点v互为邻援点。边(v,w)依附于顶点w和v,或者说边(v,w)和顶点v、w相关联。

3、有向图
- 若E是有向边(也称弧)的有限集合时,则图G为有向图弧是顶点的有序对,记为<v.w>,其中v、w是顶点,v称为弧尾,w称为弧头,<v.w>称为从顶点v到顶点w的弧,也称v邻接到w,或w邻接自v。<v, w> f <w, v
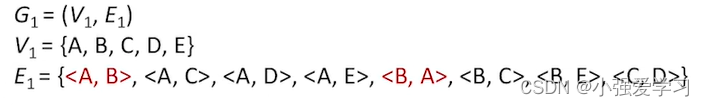 4、简单图
4、简单图
- 不存在重复边
- 不存在顶点到自身的边
5、多重图
- 图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则G为多重图
6、顶点的度
- 对于无向图: 顶点v的度是指依附于该顶点的边的条数,记为TD(v)
- 对于有向图入度是以顶点v为终点的有向边的数目,记为ID(v);出度是以顶点v为起点的有向边的数目,记为OD(v),顶点v的度等于其入度和出度之和,即TD(v) = ID(v) + OD(v)
7、其他的概念
- 路径--顶点v,到顶点v之间的一条路径是指顶点序列。
- 回路--第一个顶点和最后一个顶点相同的路径称为回路或F
- 简单路径一-在路径序列中,顶点不重复出现的路径称为简单路径。
- 简单回路--除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路
- 路径长度-路径上边的数目
- 点到点的距离从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离若从u到v根本不存在路径,则记该距离为无穷
- 无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
- 有向图中,若从顶点v到贝点w和从顶点w到顶点v之间都有路径则称这两个顶点是强连通的
- 若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图
- 若图中任何一对顶点都是强连通的,则称此图为强连通图
- 无向图的极大连通子图称为连通分量
- 有向图中的极大强连通子图称为有向图的强连通分量
- 连通图的生成树是包含图中全部顶点的一个极小连通子图
二、图的存储
1、邻接矩阵法
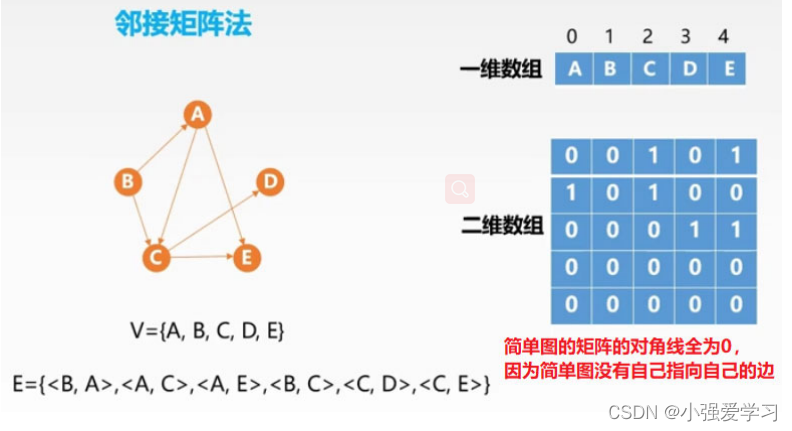
- 图的邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
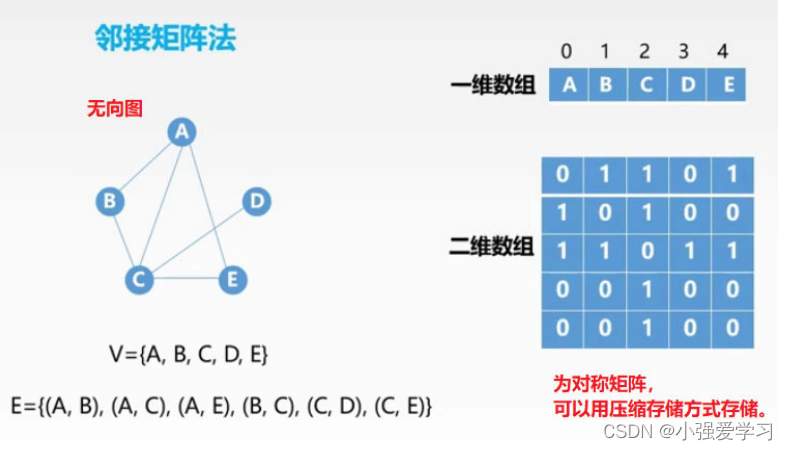
可以看出:
- 无向图的邻接矩阵一定是一个对称矩阵(即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的)。 因此,在实际存储邻接矩阵时只需存储上(或下)三角矩阵的元素。
- 对于无向图,邻接矩阵的第i ii行(或第i ii列)非零元素(或非∞ ∞∞元素)的个数正好是第i个顶点的度T D ( v i ) 。比如顶点v1 度就是1 + 0 + 1 + 0 = 2
- 求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍, A [ i ] [ j ] 就是邻接点。
- 第i个结点的度 = 第i行 (或第i)的非零元素个数
- 第i个结点的出度 =第i行的非零元素个数
- 第i个结点的入度 =第i列的非零元素个数
- 第i个结点的度 =第i行、第i列的非零元素个数之和
邻接矩阵法代码实现
#define MaxVertexNum 100 //顶点数目的最大值
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
typedef struct{
VertexType Vex[MaxVertexNum]; //顶点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, arcnum; //图的当前顶点数和弧树
}MGraph;
2、邻接表法(顺序+链式存储)
- 用顺序表存放J顶点一一顶点表:存放顶点数据+单链表表头
- 用单链表存放边一一边表(出表表):存放与顶点相连的所有边(出边)
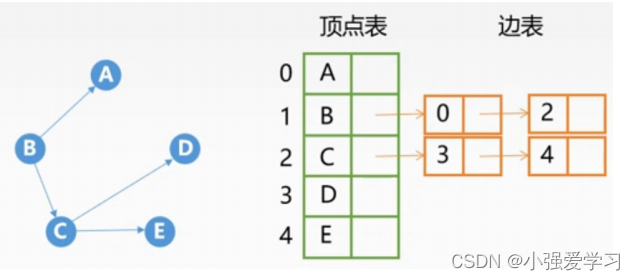
代码实现
#define MAXVEX 100 //图中顶点数目的最大值
type char VertexType; //顶点类型应由用户定义
typedef int EdgeType; //边上的权值类型应由用户定义
/*边表结点*/
typedef struct EdgeNode{
int adjvex; //该弧所指向的顶点的下标或者位置
EdgeType weight; //权值,对于非网图可以不需要
struct EdgeNode *next; //指向下一个邻接点
}EdgeNode;
/*顶点表结点*/
typedef struct VertexNode{
Vertex data; //顶点域,存储顶点信息
EdgeNode *firstedge //边表头指针
}VertexNode, AdjList[MAXVEX];
/*邻接表*/
typedef struct{
AdjList adjList;
int numVertexes, numEdges; //图中当前顶点数和边数
}
邻接表的特点:
- 对于无向图,存储空间为O(V+2 E);对于有向图,存储空间为O(V|+|El);
- 更适合用于稀疏图
- 若G为无向图,则顶点的度为该顶点边表的长度若G为有向图,则顶点的出度为该顶点边表的长度,计算入度需要遍历整个邻接表;
- 邻接表不唯一,边表结点的顺序根据算法和输入不同可能会不同

3、十字链表存储
十字链表是有向图的一种链式存储结构。
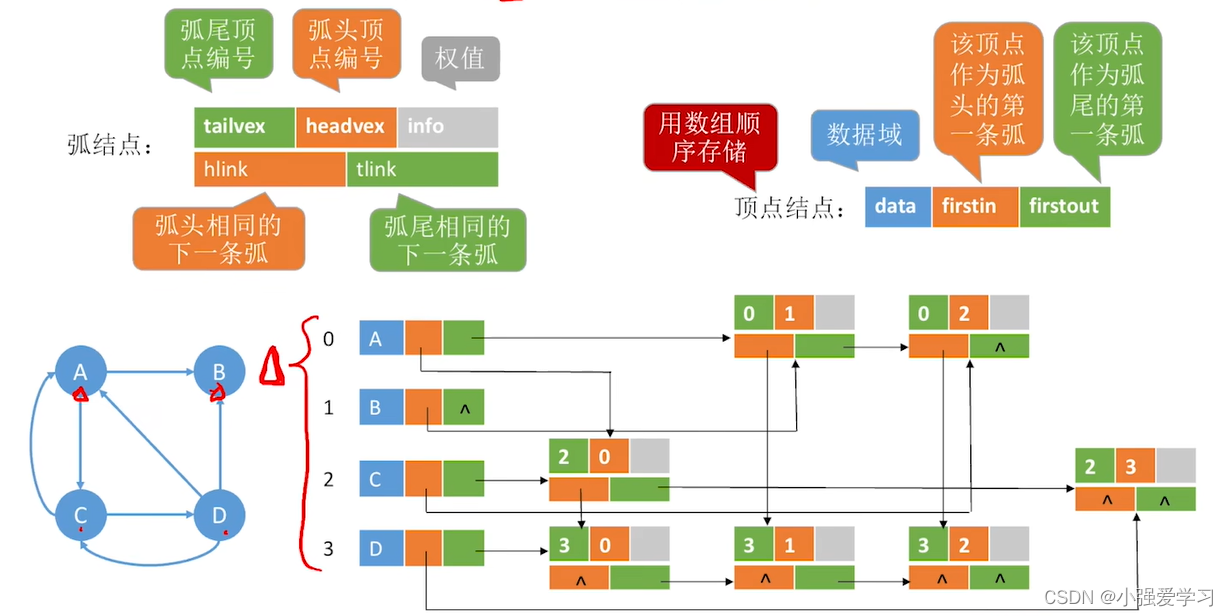
4、邻接多重表
邻接多重表是无向图的另一种链式存储结构。
三、图的基本操作

四、图的遍历
1、广度优先遍历
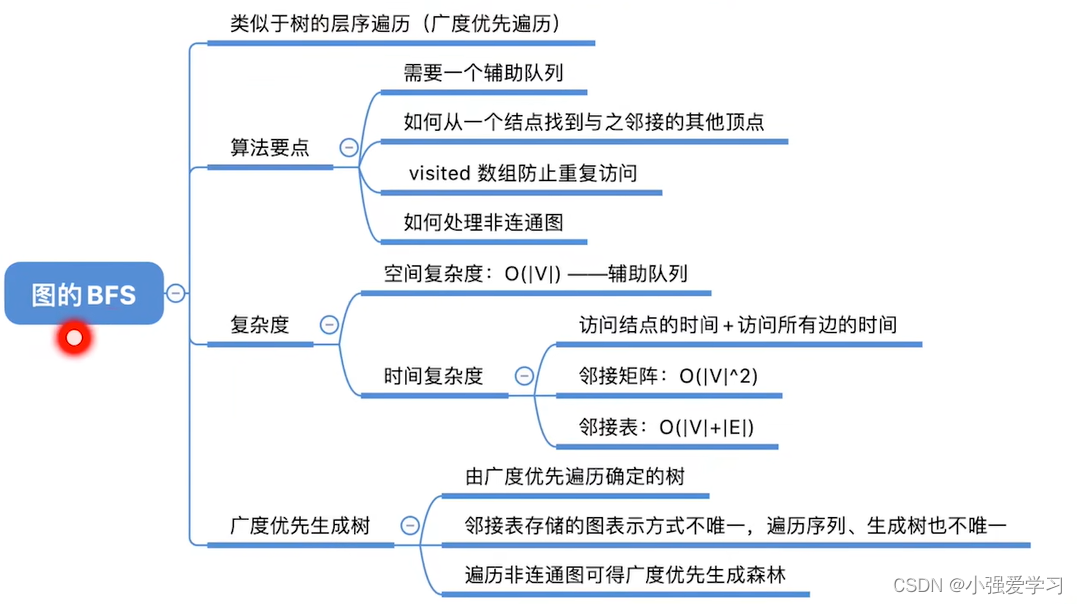
广度优先遍历 (Breadth-First-Search,BFS)要点:
- 1.找到与一个顶点相邻的所有顶点·
- 2.标记哪些顶点被访问过
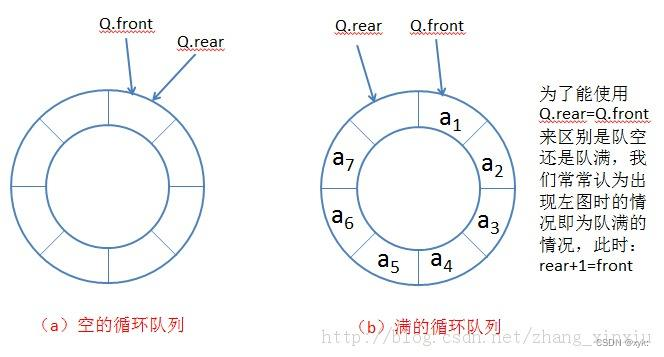
- 3需要一个辅助队列
代码实现:
/*邻接矩阵的广度遍历算法*/
void BFSTraverse(MGraph G){
int i, j;
Queue Q;
for(i = 0; i<G,numVertexes; i++){
visited[i] = FALSE;
}
InitQueue(&Q); //初始化一辅助用的队列
for(i=0; i<G.numVertexes; i++){
//若是未访问过就处理
if(!visited[i]){
vivited[i] = TRUE; //设置当前访问过
visit(i); //访问顶点
EnQueue(&Q, i); //将此顶点入队列
//若当前队列不为空
while(!QueueEmpty(Q)){
DeQueue(&Q, &i); //顶点i出队列
//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。
//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点v
for(j=FirstNeighbor(G, i); j>=0; j=NextNeighbor(G, i, j)){
//检验i的所有邻接点
if(!visited[j]){
visit(j); //访问顶点j
visited[j] = TRUE; //访问标记
EnQueue(Q, j); //顶点j入队列
}
}
}
}
}
}
2、深度优先遍历

深度优先遍历(Depth First Search),也有称为深度优先搜索,简称为DFS。
代码实现:
bool visited[MAX_VERTEX_NUM]; //访问标记数组
/*从顶点出发,深度优先遍历图G*/
void DFS(Graph G, int v){
int w;
visit(v); //访问顶点
visited[v] = TRUE; //设已访问标记
//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点,若有则返回顶点号,否则返回-1。
//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点,返回除w外顶点v
for(w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){
if(!visited[w]){ //w为u的尚未访问的邻接顶点
DFS(G, w);
}
}
}
/*对图进行深度优先遍历*/
void DFSTraverse(MGraph G){
int v;
for(v=0; v<G.vexnum; ++v){
visited[v] = FALSE; //初始化已访问标记数据
}
for(v=0; v<G.vexnum; ++v){ //从v=0开始遍历
if(!visited[v]){
DFS(G, v);
}
}
}