初阶数据结构学习记录——아홉 二叉树和堆（2）

接着上一篇

之前写过一些关于堆的代码，向下调整，向上调整算法，以及常用的几个函数。这一篇继续完善堆，难度也会有所上升。先来看上一篇文末提到的创建堆算法。

首先要有空间，要有数据，之后再形成堆。我们可以malloc一块空间，数据也可push或者创建一个数组然后拷贝过来，不过面对一个不成规则的数据如何把他们做成堆？直接用向上或向下调整都不能做到，如果说根节点的整个左子树和右子树都是大堆，那么用向下调整就合适。现在用这串数字做例子

把它变成堆的样子后，最后一层就有49 25 37。现在要把左右子树都变成大堆，如何改变？我们一块一块来改。37和28、18，49和25、19，34和65,、15和子节点们，最后整体调整。而关于18应该怎么找到，如果数组大小是n，那么18的下标就是（n-1-1）/2，用循环即可一个个调整。

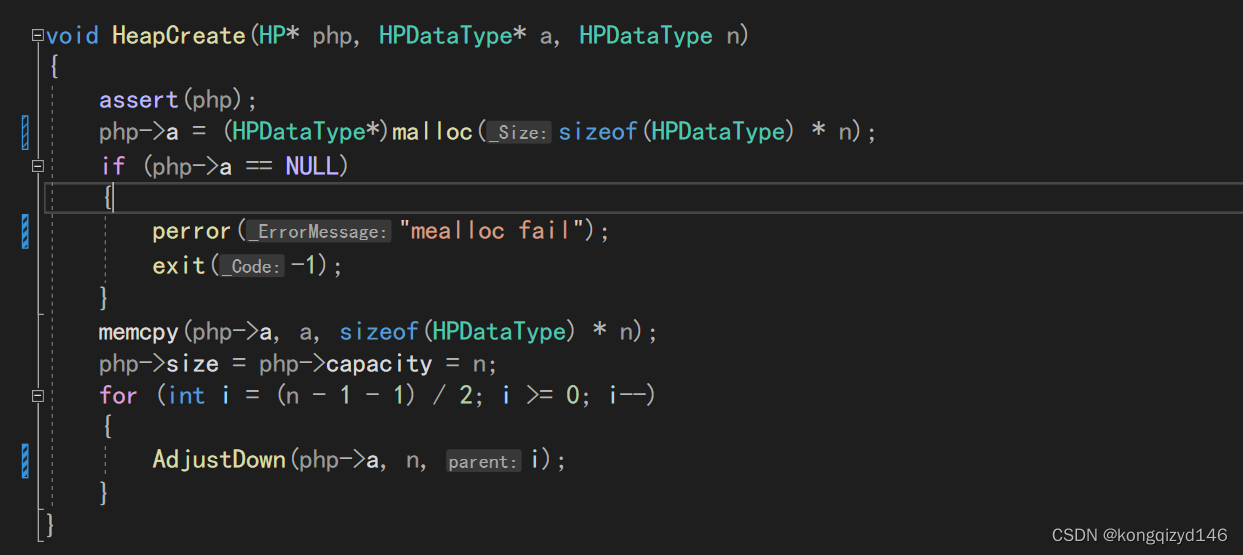
void HeapCreate(HP* php, HPDataType* a, HPDataType n)
{
   assert(php);
   php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
   if (php->a == NULL)
   {
       perror("realloc fail");
       exit(-1);
   }
   memcpy(php->a, a, sizeof(HPDataType) * n);
   php->size = php->capacity = n;
   for (int i = (n - 1 - 1) / 2; i >= 0; i--)
   {
       AdjustDown(php->a, n, i);
   }
}

测试一下

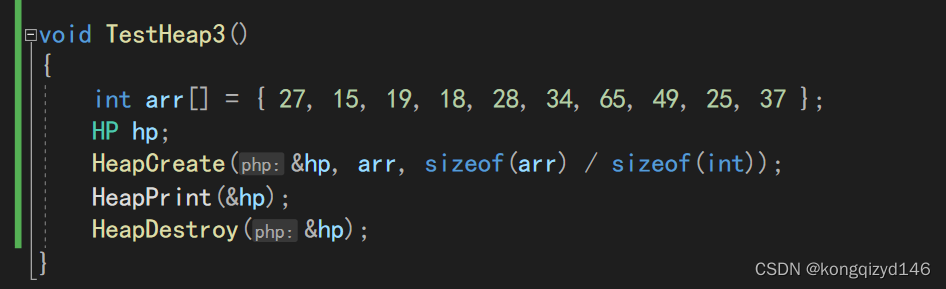
void TestHeap3()
{
   int arr[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
   HP hp;
   HeapCreate(&hp, arr, sizeof(arr) / sizeof(int));
   HeapPrint(&hp);
   HeapDestroy(&hp);
}

成功创建。

堆排序

现在做排序算法

给一个数组，通过排序算法把他们变成堆。原始的数组无序。

int arr[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
HeapSort(arr, sizeof(arr) / sizeof(int));

这样的话我们有两个方案，做向上调整或者向下调整。

   for (int i = 1; i < n; i++)
   {
       AdjustUp(a, i);
   }
   for (int i = (n - 1 - 1) / 2; i >= 0; i--)
   {
       AdjustDown(a, n, i);
   }

向上调整的思路就是默认为大堆，遍历数组看成一个个插入，插入第一个不做操作，第二个开始就进行比较，然后决定是否交换位置

向下调整的思路则是所有数据无序，不能直接进行向下调整。其实这个条件可以从pop函数里看出来，pop操作时，整体是大堆顺序，交换首尾元素，size--，这样整个堆里除了根节点，左子树和右子树都是大堆，这种情况向下调整可行。所以同样，这里就不能直接调整，但从尾开始调整是可以的。找到尾部元素的父节点，一一调整。

但是一般使用向下调整。假设是一个完全二叉树，N为节点数，h是高度。向下调整的次数是2^h -1 -h，也就是N - h，也就是N - log2(N + 1)，最后时间复杂度就是O(N)。

而向上调整最后一层的最大调整次数就是2^(h-1) * (h-1)，把它变成2^h*(h-1) / 2,也就是(N + 1)(log2N + 1) / 2, 所以仅最后一层都达到了N * log2N，所以向上调整的时间复杂度明显比向下大，而向上调整的时间复杂度就是O(N * log2N)。

在二叉树里，最后一层的节点数最多，而向下调整跳过了最后一层，直接从最后一层的父节点开始调整，并且从下到上，节点数多的调整少，而向上调整则是节点多的调整多，最后一层更是很多调整。所以不管是不是全部都要调整，向下调整次数都明显比向上少。

所以用向下调整法

向下调整选好了，接下来思考另一个问题，如果要升序的话，应该是建立大堆还是小堆？假如现在建小堆，面对一串无序的数字，如果pop掉第一个元素，把它放到另一个空间里，然后一个个插入来调整做成小堆可以，但是这样空间复杂度变高了。但是不开辟空间的话，在原始数组里调整，会发现数字之间的关系很容易乱掉，耗掉了很多时间。所以升序还是建立大堆。

大堆建好后，我们开始做升序。关于升序，我们可以把首尾元素互换一下，这样最大值出现在尾部，然后对于前面的数值进行向下调整找到次大值，排在倒数第二个位置，然后重复这个操作即可。

void AdjustDown(HPDataType* a, int n, int parent)
{
   int child = parent * 2 + 1;
   while (child < n)
   {
       //确认child指向大的那个孩子并且child要小于size
       if (child + 1 < n && a[child + 1] > a[child])
       {
           ++child;
       }
       if (a[child] > a[parent])
       {
           Swap(&a[child], &a[parent]);
           parent = child;
           child = parent * 2 + 1;
       }
       else
       {
           break;
       }
   }
}

void HeapSort(HPDataType* a, HPDataType n)//O(N * log2N)
{
   //0(N)
   for (int i = (n - 1 - 1) / 2; i >= 0; i--)
   {
       AdjustDown(a, n, i);
   }
   int end = n - 1;
   //O(N * log2N)
   while (end > 0)
   {
       Swap(&a[0], &a[end]);
       AdjustDown(a, end, 0);
       end--;
   }
}

当然如果向下调整里a[child + 1] > a[child]以及a[child] > a[parent]都改成<，那么就是降序了。

TOPK问题

接着来下一个问题。

在一些数据中找到十个最大的数据，把这个数字设为k，也就是找到前k个大的数据。当然我们可以一个个比较，但是正因为数据量不确定，所以情况不能这样简单。假设是有N个数字，N为十亿，百亿个，如果还是之前的办法是肯定不可行的。我们现在用堆来解决。堆如何找到最大的那k个数字？如果建立一个大堆，放进所有数字，那么最大的那几个一定是在前面的，这样取堆顶，然后pop掉（pop里面有向下调整），再取堆顶，就能找到前十个了。虽然这个思路可以，但是忘了一个重要的事，还是数据很大的问题。百亿个数字，建立一个百亿数字的大堆，这需要占用多少内存？算下来，几十G。所以，这个方法其实是不现实的。单论这个思路来讲，时间复杂度是N + logN * K，空间复杂度是O（1）。

现在换另一个思路，假设k就是10吧，前10个大的数字集合起来叫做O，用整个数据集里前10个数字作一个小堆，这个小堆都有哪些数字不需要担心，即使有O里面的数字也可，因为它一定大于其它所有的数字，也一定在堆里面靠下点的位置。之后遍历剩下的数字，每个都和现有小堆的堆顶比较，小于就无操作，大于就进堆，如果遇到O里面的数字，假设编号是O1 - O10，无论哪个数字，都一定会进堆，然后放在下面。假如遍历到最后时，才遇到O1或者O10也没有关系，遇到O1会进堆，此时其他数字都进来了，那么排在第一层的就相对来说是一个小数字，进入后不断向下调整，堆顶就会变为O10，最后整个堆就是O里的数字。O10也一样，一定会替换掉堆顶，自己做堆顶。其他哪一个O里的数字都一样。

而这样的时间复杂度是K + (N - K) * logK，空间复杂度为K。这种做法会直接在磁盘里读取数据，空间问题也就解决了。

接下来是代码展示。

先随机1000个数字，范围在10000之内

向下调整改成小堆

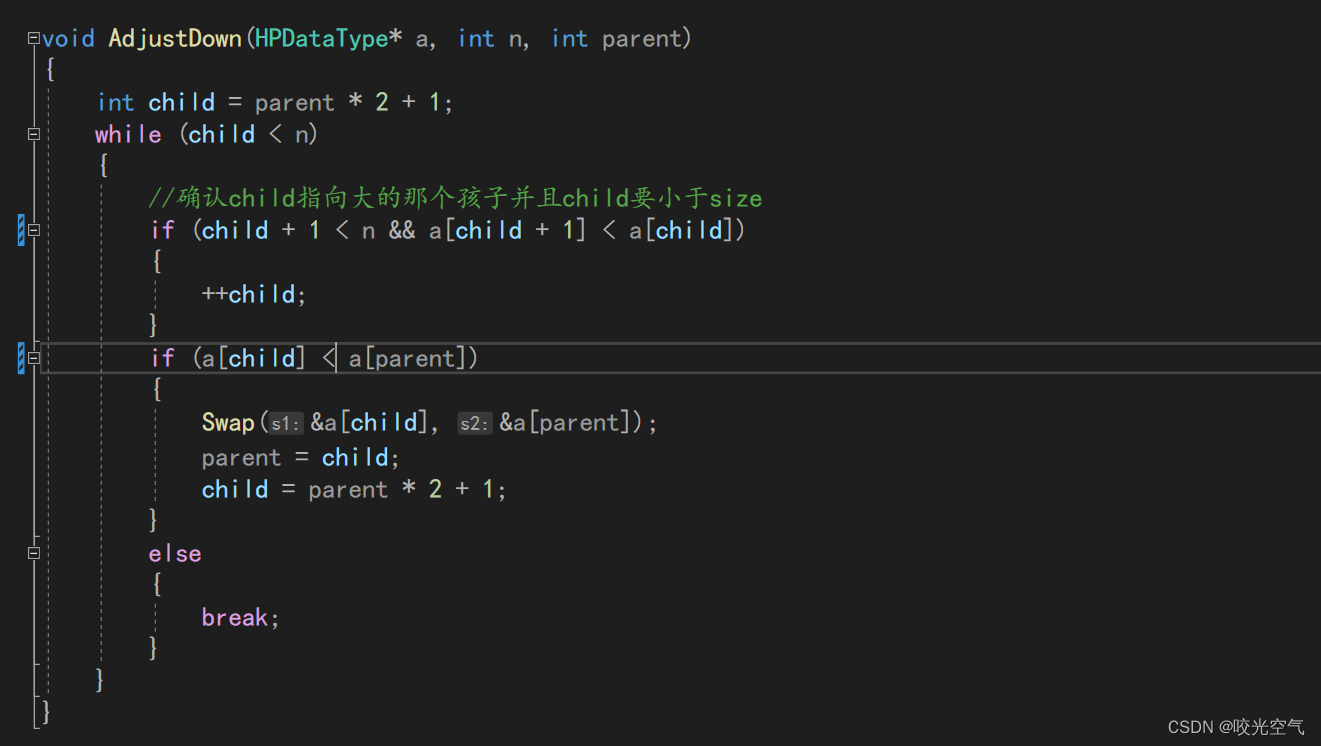
a[child + 1]以及a[child]后的 > 改成 <即为小堆。

测试函数

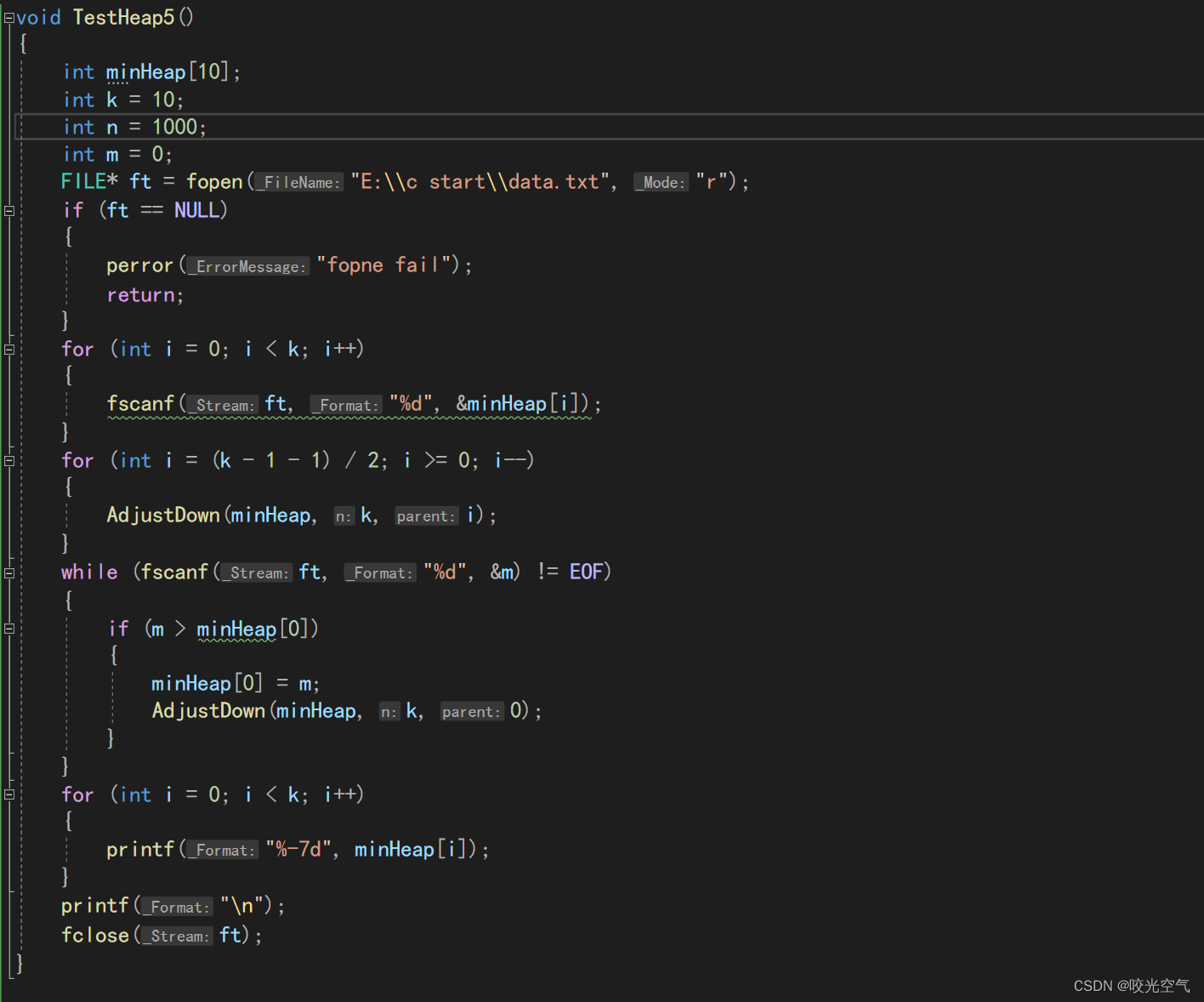
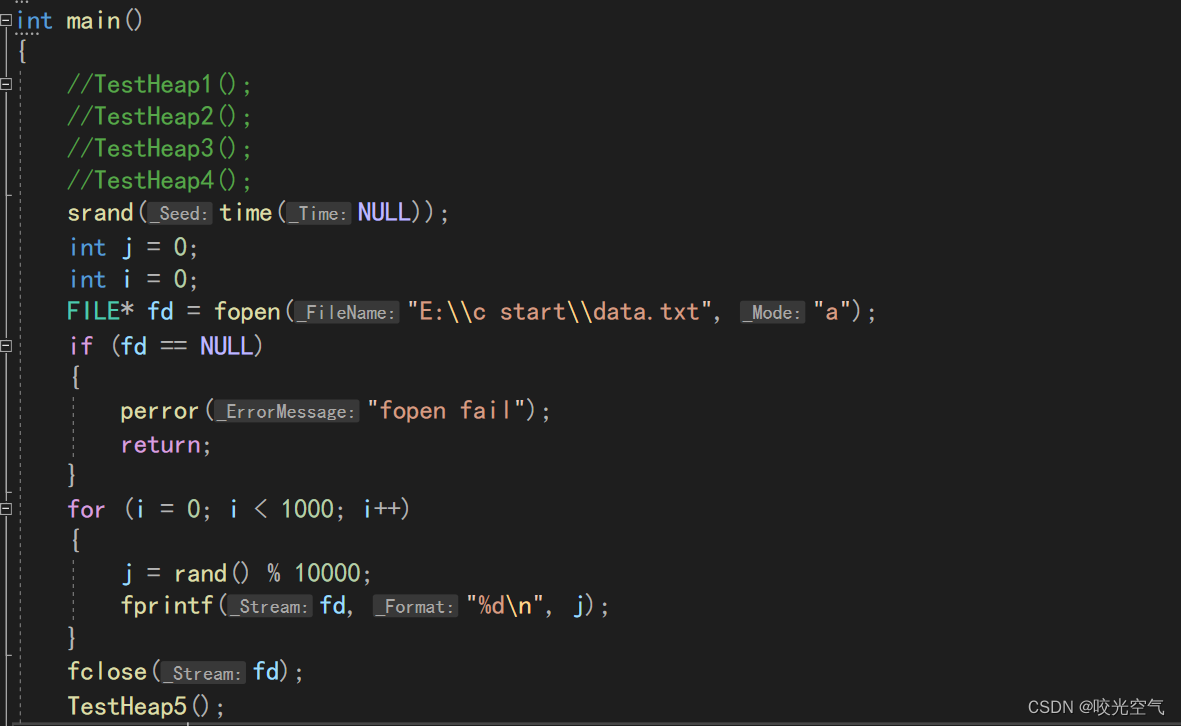
这里数组也可以malloc。

但是这还有一个问题，程序给出的结果就真的是最大的那10个吗？我们应该怎么判定？其实我们可以主动对数据做点动作，改变k个数据，让他们变成毫无疑问的最大。这里我把生成随机数也放进测试函数里。

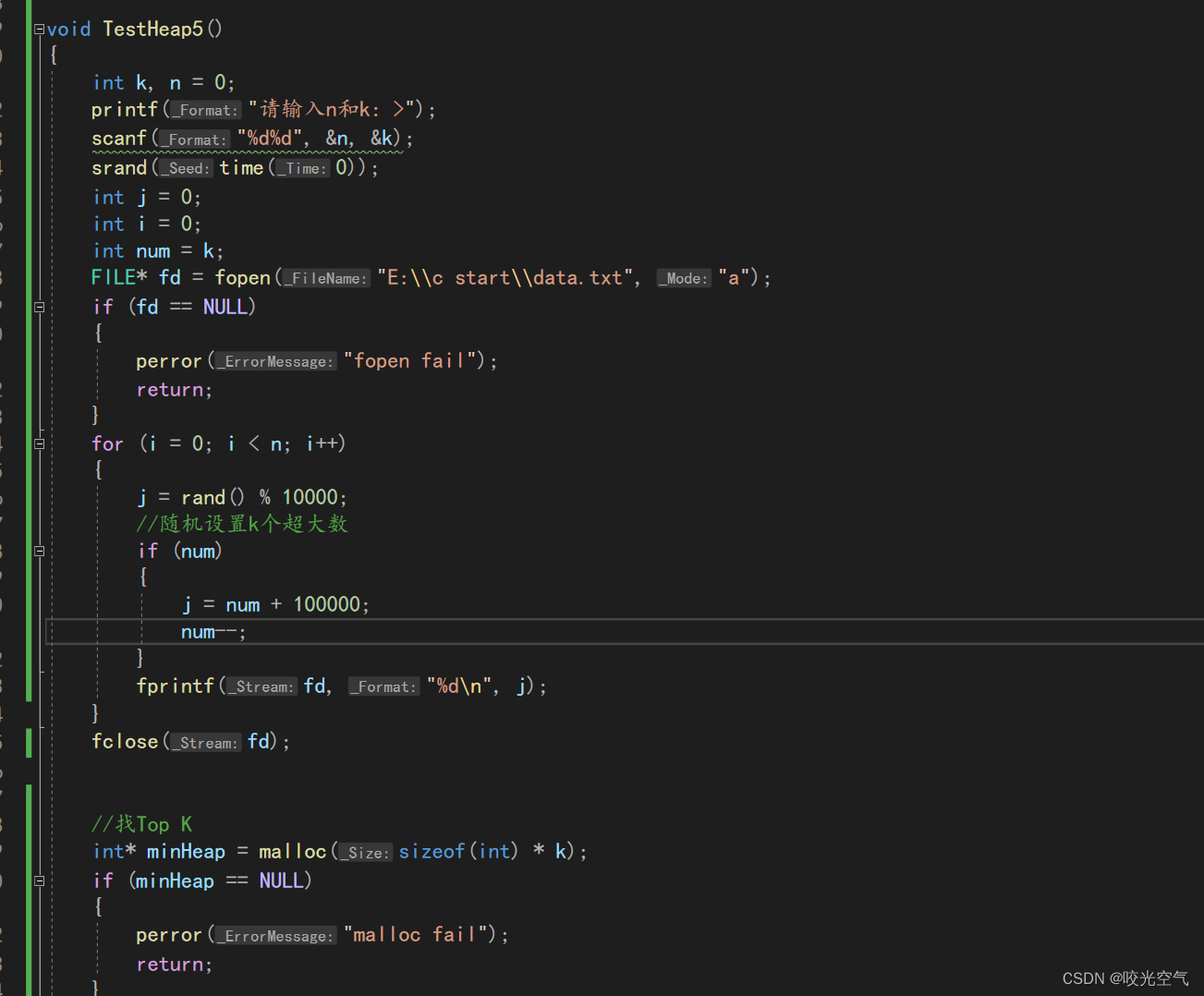
所以最大的几个就出来了。

放出这篇所有代码

创建堆

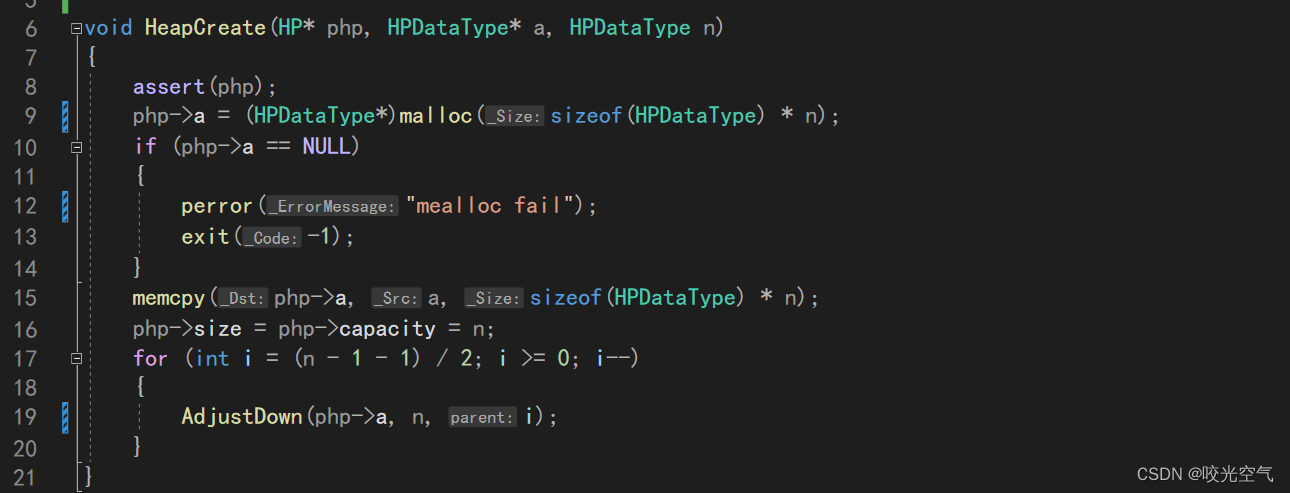
void HeapCreate(HP* php, HPDataType* a, HPDataType n)
{
   assert(php);
   php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
   if (php->a == NULL)
   {
       perror("mealloc fail");
       exit(-1);
   }
   memcpy(php->a, a, sizeof(HPDataType) * n);
   php->size = php->capacity = n;
   for (int i = (n - 1 - 1) / 2; i >= 0; i--)
   {
       AdjustDown(php->a, n, i);
   }
}

排序

Top K

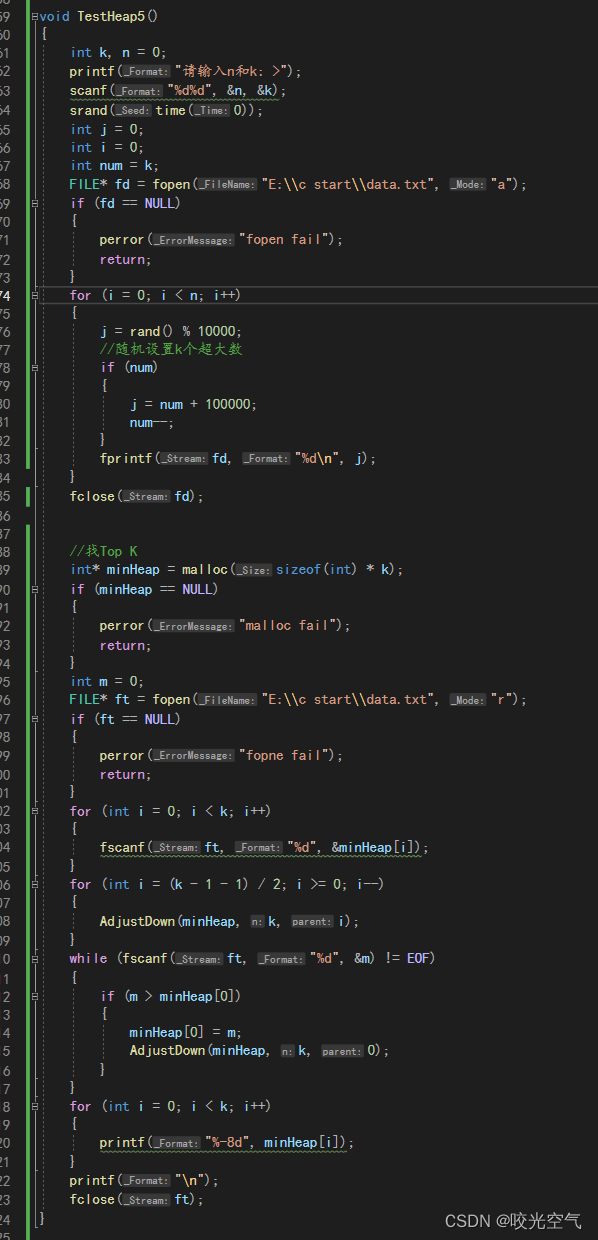
由于网络极致不要脸地无法十分钟传输一张图片，所以这里只能展示改过后的代码，而图片则没有。其实也不算是网络的事，是学校扯淡到极其可笑了。改动位置是随机设置k个超大数那里。

void TestHeap5()
{
   int k, n = 0;
   printf("请输入n和k: >");
   scanf("%d%d", &n, &k);
   srand(time(0));
   int j = 0;
   int i = 0;
   int num = k;
   FILE* fd = fopen("E:\\c start\\data.txt", "a");
   if (fd == NULL)
   {
       perror("fopen fail");
       return;
   }
   for (i = 0; i < n; i++)
   {
       j = rand() % 10000;
       //随机设置k个超大数
       if (num)
       {
           j = num + 100000;
           num--;
       }
       fprintf(fd, "%d\n", j);
   }
   fclose(fd);

   //找Top K
   int* minHeap = malloc(sizeof(int) * k);
   if (minHeap == NULL)
   {
       perror("malloc fail");
       return;
   }
   int m = 0;
   FILE* ft = fopen("E:\\c start\\data.txt", "r");
   if (ft == NULL)
   {
       perror("fopne fail");
       return;
   }
   for (int i = 0; i < k; i++)
   {
       fscanf(ft, "%d", &minHeap[i]);
   }
   for (int i = (k - 1 - 1) / 2; i >= 0; i--)
   {
       AdjustDown(minHeap, k, i);
   }
   while (fscanf(ft, "%d", &m) != EOF)
   {
       if (m > minHeap[0])
       {
           minHeap[0] = m;
           AdjustDown(minHeap, k, 0);
       }
   }
   for (int i = 0; i < k; i++)
   {
       printf("%-8d", minHeap[i]);
   }
   printf("\n");
   fclose(ft);
}