一、题目描述

在这里插入图片描述

示例 1：

输入：
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]
解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示

1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的（例如，一个空的队列不会调用 pop 或者 peek 操作）

二、思路分析

可以先看看这一篇：用队列实现栈

好，看完题目的描述，我们来分析一下去求解这道题目

我们知道，栈与队列的原理刚好相反，对于栈是【FILO】，对于队列是【FIFO】。这就需要我们灵活地去使用这两种数据结构进行解题。对于本题，我的思路是这样的： 因为需要使用栈来实现队列，那还需要像我们上一题那样将两个队列倒来倒去实现一个出栈的操作吗？
答案是：不需要，对于这一题而言，我们需要有一个明确的思路，也是去定义两个栈，一个栈专门入数据，一个栈专门出数据，具体的实现在下面👇

三、代码详解

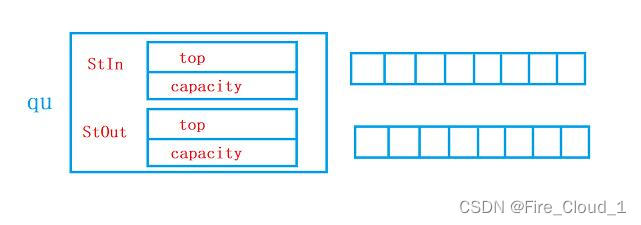
1、结构声明与展开剖析

可以看到，【StIn】是专门用来入数据的，【StOut】是专门用来出数据的；接着看到初始化创建这一块，一样对这两个栈进行一个初始化，首先由【qu】访问到这个两个栈，接着传入相应的地址进行初始化操作

typedef struct {
    ST stIn;
    ST stOut;
} MyQueue;

MyQueue* myQueueCreate() {
    MyQueue* qu = (MyQueue *)malloc(sizeof(MyQueue));
    InitStack(&qu->stIn);
    InitStack(&qu->stOut);

    return qu;
}

以下是这个结构的整体形式

然后的话来讲几个重要的接口算法实现

2、入队【入栈思想】

首先的话就是这个入队了，因为我们使用栈来模拟，而且有专门只入数据的栈，因此直接将要放入队列的数据放到这个【StIn】中即可

PushStack(&obj->stIn, x);       //入栈操作均放入stIn

3、获取队头【出栈思想】

接下去在首先讲出队操作之前我先讲讲如果获取队头这个接口，也就是peek()
首先你会想到的一定是直接去调用我们栈中的Top()这个接口，去【StOut】中取数据，确实是可以取出来，但是当这个【StOut】为空的时候怎么办呢？因为需要去做一个处理

return StackTop(&obj->stOut);

但这个【StOut】为空的时候，我们就可以将【StIn】中的数据放入【StOut】中，直至【StIn】为空为止。因为我们规定过【StIn】只入数据，【StOut】只出数据，所以要将这个【StIn】中的数据都倒到【StOut】中才可（这句话看清楚了，不要被我绕晕😵，或者你直接看代码吧）

if(StackEmpty(&obj->stOut))     //如果stOut为空，则进行一个倒栈操作
{
    while(!StackEmpty(&obj->stIn))
    {
        PushStack(&obj->stOut, StackTop(&obj->stIn));
        PopStack(&obj->stIn);
    }
}

4、出队【复用思想】

有了【peek()】这个接口，我们在实现出队接口的时候就不需要再去写一个了，只需要去进行一个复用即可。接着Pop()出【StOut】中的一个数据

int peek = myQueuePeek(obj);
PopStack(&obj->stOut);

return peek;

5、逐步算法图解

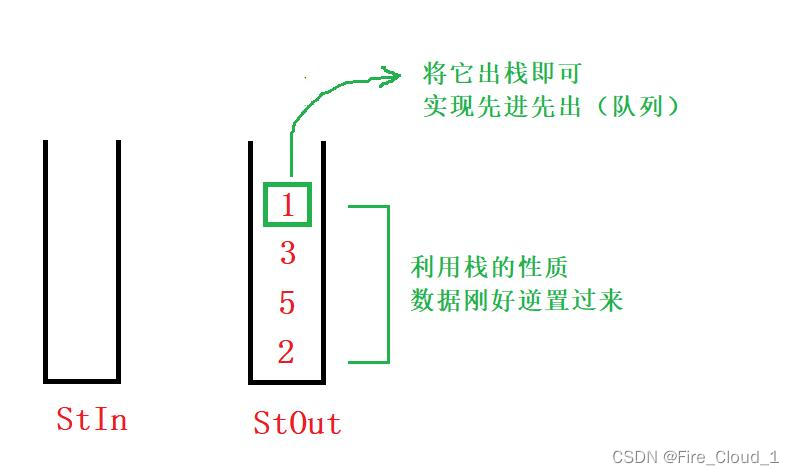
接下去我们通过算法图解来步步分析一下，首先看到【StOut】为空，因为需要将【StIn】中的数据尽数放入其中

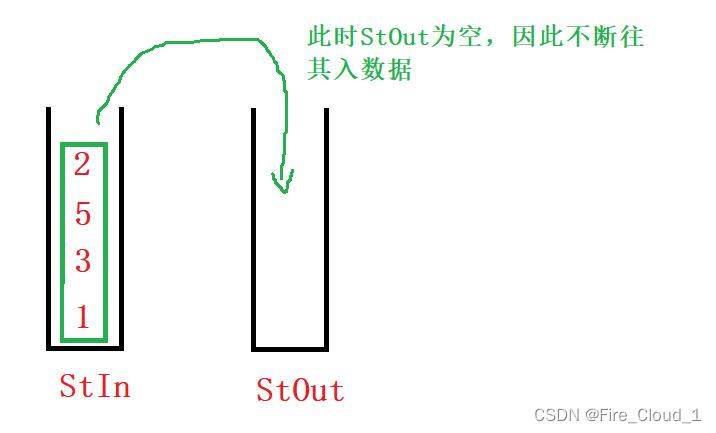
在这里插入图片描述

接着的话当全部数据一一过来后可以看到所有数据刚好实现了一个逆置的效果，接着出栈栈顶元素即可，就可以实现队列的一个FIFO的性质🎋

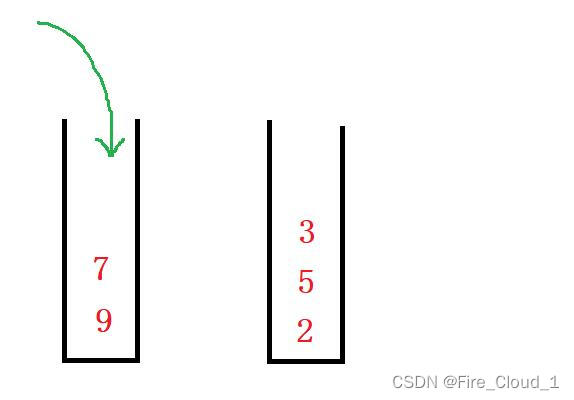
继续入两个数据

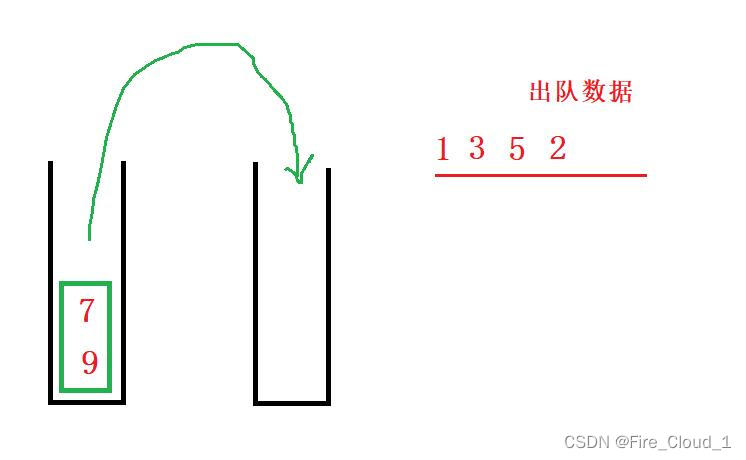
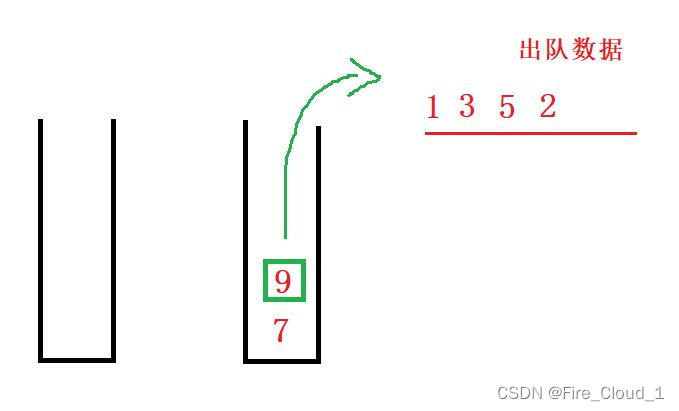
当连续执行完3次出队后，可以看到出队的顺序就是先进先出，接下去要继续出数据，因为【StOut】空了，所以继续将刚入的9和7放进来

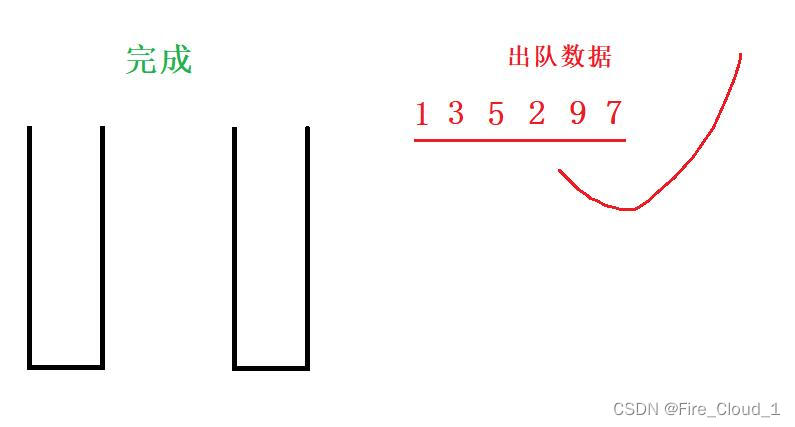
最后出队完成后就是利用两个栈实现的模拟队列入队出队后的序列

四、整体代码展示

💻C语言代码实现

题目代码使用的是C语言实现

typedef int STDataType;
typedef struct Stack {
	STDataType* a;
	int top;		//栈顶指针
	int capacity;	//容量
}ST;

/*初始化栈*/
void InitStack(ST* st);

/*销毁栈*/
void DestroyStack(ST* st);

/*入栈*/
void PushStack(ST* st, STDataType x);

/*出栈*/
void PopStack(ST* st);

/*返回栈顶元素*/
STDataType StackTop(ST* st);

/*判空*/
bool StackEmpty(ST* st);

/*栈的元素个数*/
int StackSize(ST* st);

//--------------------------------
typedef struct {
    ST stIn;
    ST stOut;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* qu = (MyQueue *)malloc(sizeof(MyQueue));
    InitStack(&qu->stIn);
    InitStack(&qu->stOut);

    return qu;
}

void myQueuePush(MyQueue* obj, int x) {
    PushStack(&obj->stIn, x);       //入栈操作均放入stIn
}

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->stIn) && StackEmpty(&obj->stOut);
}

int myQueuePop(MyQueue* obj) {
    int peek = myQueuePeek(obj);
    PopStack(&obj->stOut);

    return peek;
}

int myQueuePeek(MyQueue* obj) {
    if(StackEmpty(&obj->stOut))     //如果stOut为空，则进行一个倒栈操作
    {
        while(!StackEmpty(&obj->stIn))
        {
            PushStack(&obj->stOut, StackTop(&obj->stIn));
            PopStack(&obj->stIn);
        }
    }
    return StackTop(&obj->stOut);
}

void myQueueFree(MyQueue* obj) {
    DestroyStack(&obj->stIn);
    DestroyStack(&obj->stOut);

    free(obj);
}

//--------------------------------
/*初始化栈*/
void InitStack(ST* st)
{
	assert(st);		//警惕随意操作，传入空指针
	st->a = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (st->a == NULL)
	{
		perror("fail mallic");
		exit(-1);
	}
	st->top = 0;		//初始化为0表示指向当前栈顶元素的后一元素
	st->capacity = 4;
}

/*销毁栈*/
void DestroyStack(ST* st)
{
	assert(st);
	free(st->a);
	st->a = NULL;
	st->top = st->capacity = 0;
}

/*入栈*/
void PushStack(ST* st, STDataType x)
{
	//栈满扩容逻辑
	if (st->top == st->capacity)
	{
		//初始化时已经malloc开辟过空间了，因此无需考虑容量为空的情况
		STDataType* tmp = (STDataType*)realloc(st->a, st->capacity * 2 * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("fail realloc");
			exit(-1);
		}
		st->a = tmp;
		st->capacity *= 2;
	}
	st->a[st->top] = x;		//top指向栈顶元素的后一元素，因此直接入栈即可
	st->top++;		//然后栈顶指针后移，为下一次入栈做准备
}

/*出栈*/
void PopStack(ST* st)
{
	assert(st);
	//assert(st->top > 0);
	assert(!StackEmpty(st));

	st->top--;
}

/*返回栈顶元素*/
STDataType StackTop(ST* st)
{
	return st->a[st->top - 1];
}

/*判空*/
bool StackEmpty(ST* st)
{
	return (st->top == 0);
}

/*栈的元素个数*/
int StackSize(ST* st)
{
	return st->top;
}

/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/