如果有兴趣了解更多相关内容，欢迎来我的个人网站看看：瞳孔空间

搜索是人工智能中的一个基本问题，并与推理密切相关。搜索策略的优劣将直接影响到智能系统的性能与推理效率。

一：搜索的基本概念

搜索：根据问题的实际情况不断寻找可利用的知识，构造出一条代价较小的推理路线，使问题得到圆满解决的过程。包括两方面：

• 找到从初识事实到问题最终答案的一条推理路径
• 找到的这条路径在时间和空间上复杂度最小

搜索的分类(按是否使用启发信息)：

• 盲目搜索(Uninformed search)：盲目搜索按预定的控制策略进行搜索，搜索过程中获得的中间信息不用来改变搜索策略。搜索总是按预定的路线进行，不考虑问题本身的特性，这种搜索有盲目性，效率不高，不利于求解复杂问题。即不利用领域知识来帮助搜索
• 启发式搜索(Heuristic search, Infomed search)：启发式搜索中利用问题领域相关的信息作为启发信息，用来指导搜索朝着最有希望的方向前进，提高搜索效率并力图找到最优解

启发式搜索需要利用问题领域相关的信息帮助搜索，但并不是对每一类问题都容易抽取出启发信息，所以在很多情况下仍然需要盲目搜索。

搜索的适用情况：不良结构或非结构化问题；难以获得求解所需的全部信息；没有现成的算法可供求解使用

搜索问题的形式化表示：搜索首先要将问题进行形式化表示，常用的形式化表示方式有状态空间法、与或树表示法(问题归约法)等

搜索策略常用评价指标：

• 完备性(Completeness)：如果问题有解，算法就能找到，称此搜索方法是完备的
• 最优性(Optimality)：如果解存在，总能找到最优解
• 时间复杂度(Time Complexity)
• 空间复杂度(Space Complexity)

二：问题的状态空间表示

2.1：概念

状态(state)：事物是运动的、变化的，为描述问题的运动、变化，定义一组变量描述问题的变化特征和属性

• 形式化表示：(s₁,s₂…s_i,…,s_n)
• 当对每一个分量都给以确定的值时，就得到了一个具体的状态

操作符(Operator)：也称为算符，它是把问题从一种状态变换为另一种状态的手段

• 操作可以是一个机械步骤，一个运算，一条规则或一个过程
• 操作可理解为状态集合上的一个函数，它描述了状态之间的关系

状态空间(State space)：用来描述一个问题的全部状态以及这些状态之间的相互关系。常用一个三元组表示为：(S,F,G)

• S为问题的所有初始状态的集合
• F为操作(函数、规则等)的集合
• G为目标状态的集合

状态空间图：状态空间的有向图表示

• 结点(节点)：节点表示问题的状态
• 弧(有向边)：标记操作符；可能的路径代价

下图即为状态空间图，S_i，S_j为两个表示状态的节点；O₁是导致状态变化的操作符；cost(S_i,S_j)是从S_i变化到S_j的代价(花费)

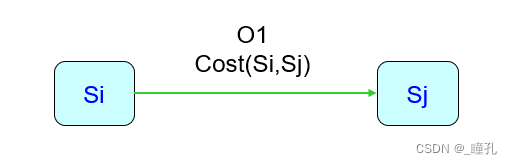
状态空间法求解问题的基本过程：

• 首先为问题选择适当的"状态"及“操作”的形式化描述方法
• 然后从某个初始状态出发，每次使用一个满足前提条件的"操作"，并且此操作产生了新的状态，递增地建立起操作序列，直到达到目标状态为止
• 此时，由初始状态到目标状态所使用的算符(操作符)序列就是该问题的一个解

2.2：例题

2.2.1：八数码问题

八数码问题也叫九宫问题，是人工智能中状态搜索中的经典问题，其中，该问题描述为：在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

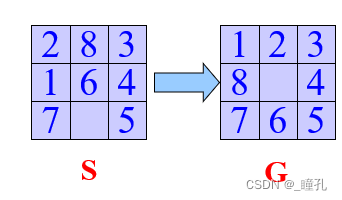
解法：

状态表示：

定义操作符（产生式规则）：

状态空间搜索：

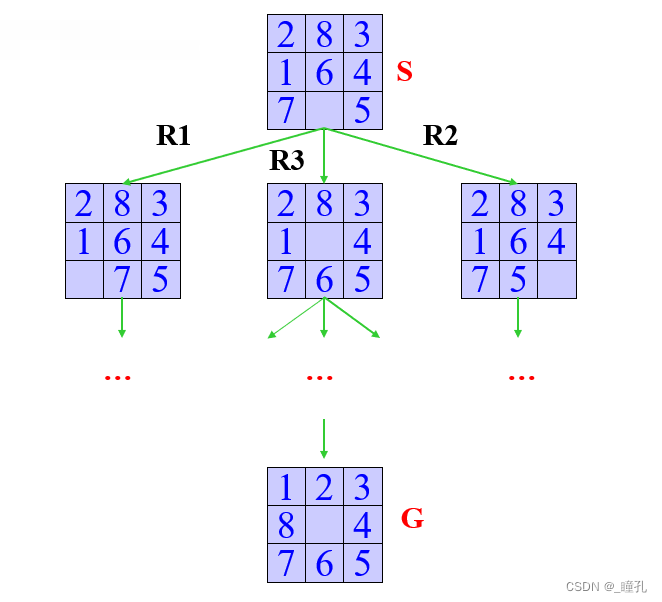
这其实不是解法，只是用状态空间表示了八数码问题，下面两个问题也是这样。如果想了解解法，可以继续往下看，在启发式搜索的内容中会介绍具体解法。但更多更详细的八数码解法，建议看看这个博客：八数码问题

2.2.2：TSP问题

TSP(Traveling Salesman Problem)问题，即旅行商问题。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。如下图，旅行商从A出发，请找出一条花费最少的旅行路径。

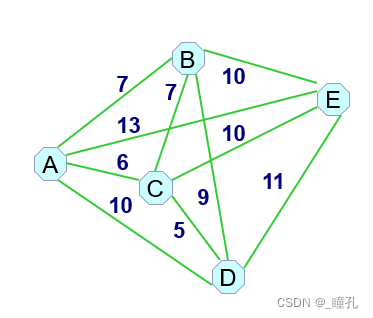
解：

状态表示：

定义操作符：

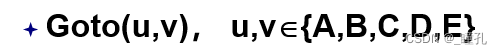
状态空间搜索：

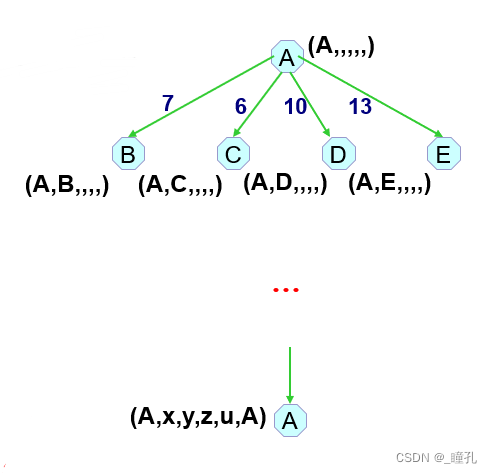
计算花费的例子：

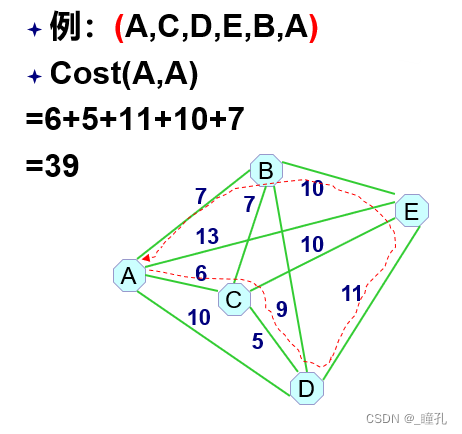
同样，这也没有真正解决TSP问题，只是用状态空间表示了这个问题，具体解决方案可以参照下面的启发式搜索内容，当然更详细的解决方案我还是推荐这篇文章：智能优化算法解决TSP旅行商问题–小总结

2.2.3：过河问题

在河的左岸有3个传教士、3个野人和一条船，传教士们想用这条船把所有人都运过河去，但有以下条件限制：

1. 修道士和野人都会划船，但船每次最多只能运2个人；
2. 在任何岸边野人数目都不能超过修道士，否则修道士会被野人吃掉。

假定野人会服从任何一种过河安排，请规划出一个确保传道士安全过河的计划。

解：

状态表示：

操作符(产生式规则)：


状态空间搜索：

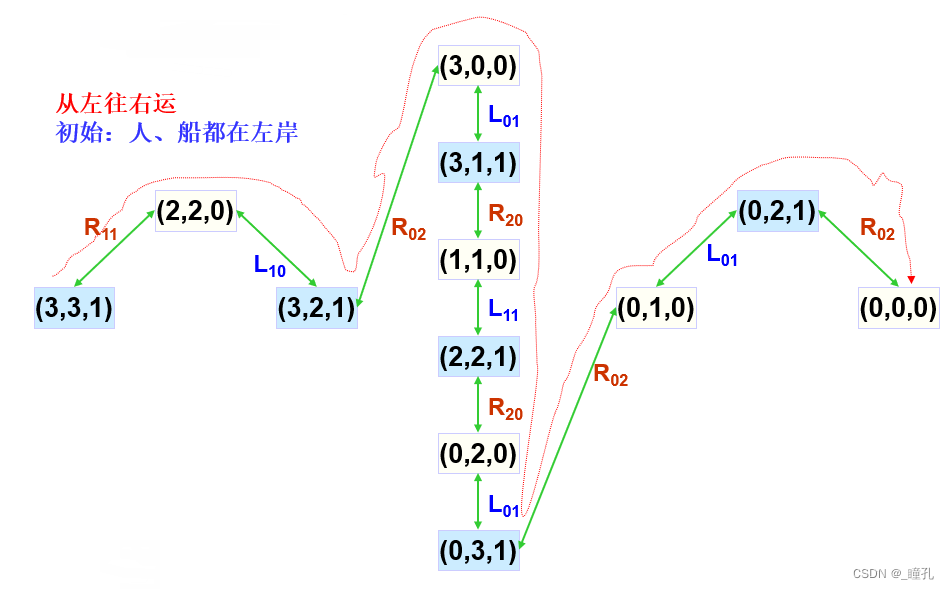
具体解法可以参考：野人传教士过河问题

三：状态空间搜索

3.1：基本概念

状态空间搜索的基本思想：先把问题的初始状态作为当前扩展节点对其进行扩展，生成一组子节点，然后检查问题的目标状态是否出现在这些子节点中。若出现，则搜索成功，找到了问题的解；若没出现，则再按照某种搜索策略从已生成的子节点中选择一个节点作为当前扩展节点。重复上述过程，直到目标状态出现在子节点中或者没有可供操作的节点为止。所谓对一个节点进行“扩展”是指对该节点用某个可用操作进行作用，生成该节点的一组子节点。

扩展节点：对某一节点(状态)，选择合适的操作符作用在节点上，使产生后继状态(子节点)的操作。类似数据结构中的寻找邻接点，但这里的邻接点是选择操作后产生的。

open表和closed表：这两个表用来存放节点，Open表存放未扩展节点，Closed表存放已扩展节点和待扩展结点，也可根据需要扩展表的结构，比如加入代价字段等。两个表的结构可以相同，大致如下：

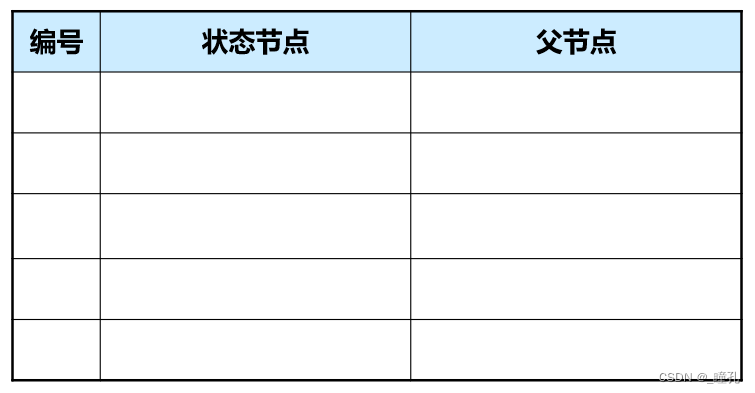
3.2：图搜索一般过程

1. 建立一个只含初始状态节点S的搜索图G，建立一个OPEN表，用来存放未扩展节点，将S放入
   OPEN表中
2. 建立一个CLOSED表，用来存放已扩展和待扩展节点，初始为空
3. LOOP：若OPEN为空，则失败、退出
4. 选择OPEN表中的第一个节点，将其移到CLOSED表中，称此节点为n节点
5. 若n为目标节点，则成功、退出。此解是追踪图G沿着指针从n到S这条路径得到的。
6. 扩展n节点，生成n的后继节点集合M=M1+M2+M3，其中n的后继结点分为3种情况。设M1表示图G中新结点(最新生成的)；M2在图G中已经存在，处于OPEN表中；M3在图G中已经存在，且已经在CLOSED表中：
   • 对M1型结点，加入到图G中，并放入OPEN表中，设置一个指向父节点n
     的指针;(DS中的未访问邻接点)
   • 对M2型结点，已经在OPEN中，确定是否需要修改父节点指针;(DS中
     已访问邻接点，但这个顶点的邻接点未搜索)
   • 对M3型结点，已经在CLOSED表中，确定是否修改其父结点指针;是否
     修改其后裔节点的指针;(DS中已访问邻接点，且这个顶点的邻接点都已经搜索过)
7. 按某一控制策略，重新排序OPEN表
8. goto LOOP

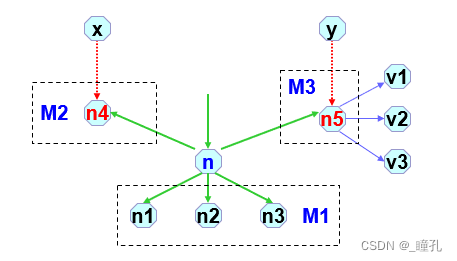
图搜索的几点说明：

1. 这是状态空间的一般搜索过程，具有通用性，后面讨论的各种搜索策略都是此过程的一个特例。不同特例的区别在于OPEN表的排序方式不同
2. 扩展节点n，生成的子节点，分为三种情况：M1是图G中没有的新节点；M2是已在图G中，但没有被扩展，即在OPEN表中；M3是已在图G中，且已经被扩展生成了子节点，即已在CLOSED表中

四：状态空间盲目搜索

盲目搜索按预定的控制策略进行搜索，搜索过程中获得的中间信息不用来改变搜索策略。搜索总是按预定的路线进行，不考虑问题本身的特性，这种搜索有盲目性，效率不高，不利于求解复杂问题。

4.1：广度优先搜索

广度优先搜索(BFS-Breadth First Search)：由近及远逐层访问图中顶点(典型的层次遍历)。

节点深度：起始节点S(根节点，图中选定起始搜索顶点)深度为0；其他节点等于父节点深度加1。

基本思想：从初始节点S开始，依据到S的深度，逐层扩展节点并考察其是否目标节点。在第n层节点没有完全扩展之前，不对第n+1层节点进行扩展。即：OPEN表排序策略为新产生的节点放到OPEN表的末端。

BFS遍历搜索算法：从初始状态节点S出发广度优先搜索遍历图的算法bfs(S)

1. 访问S
2. 依次访问S的各邻接点
3. 设最近一层访问序列为V_i1，V_i2，…,V_ik，则依次访问V_i1，V_i2，…，V_ik的未被访问过的邻接点
4. 重复3，直到找不到未被访问的邻接点为止

例如，对下图进行广度优先遍历：

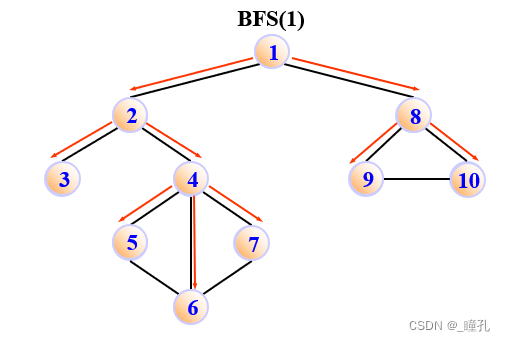
顶点访问序列为：1 -> 2 -> 8 -> 3 -> 4 -> 9 -> 10 -> 5 -> 6 -> 7

BFS(1)的生成树：

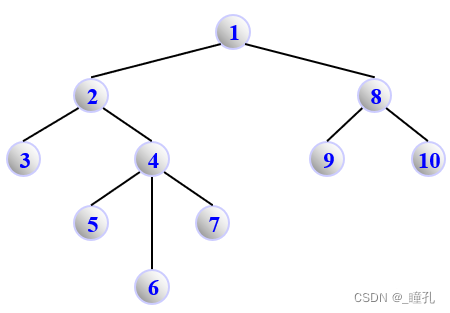
状态空间广度优先搜索：

1. 把初始节点S0放入Open表中
2. 如果Open表为空，则问题无解，失败退出
3. 把Open表的第一个节点取出放入Closed表，并记该节点为n
4. 考察节点n是否为目标节点。若是，则得到问题的解，成功退出
5. 若节点n不可扩展，则转第2步;
6. 扩展节点n，将其子节点放入Open表的尾部，并为每一个子节点设置指向父节点的指针，然后转第2步

八数码问题的BFS解法：

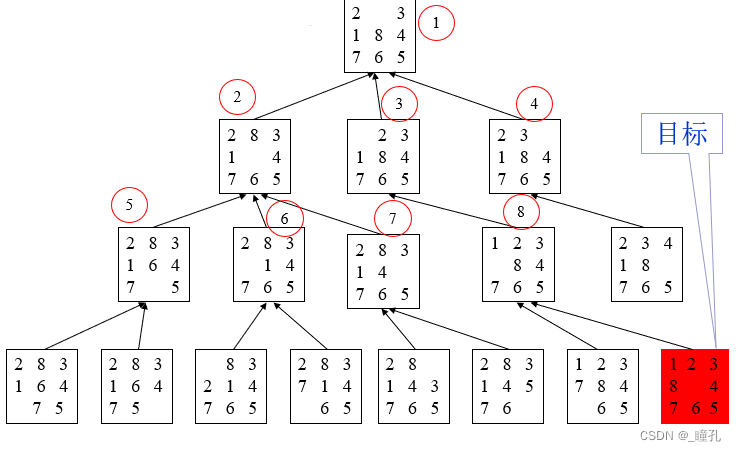
性能：

• 完备的
• 最优的一对搜索深度指标
• 时间复杂度：O(a^b)
  • 树的分枝因子(度)：树中最大的子节点数(按最坏情况考虑)设为a
  • 搜索深度：b
• 空间复杂度：O(a^b)

优点：

• 只要问题有解，则总可以得到解，而且是最短路径(深度)的解

缺点：

• 当目标节点距离初始节点较远时会产生许多无用的节点，搜索效率低
• 空间是大问题(和时间相比)

应用实例：搜索引擎的网络爬虫——网页超链接的广度优先搜索：处理一个网页上的所有超链接后，再进入下一层页面处理

搜索引擎所用的第一代网络爬虫主要是基于传统的图算法，如宽度优先或深度优先算法来索引整个Web，一个核心的URL集被用来作为一个种子集合，这种算法递归的跟踪超链接到其它页面，而通常不管页面的内容，因为最终的目标是这种跟踪能覆盖整个Web。这种策略通常用在通用搜索引擎中，因为通用搜索引擎获得的网页越多越好，没有特定的要求.

4.2：深度优先搜索

深度优先搜索(DFS-Depth First Search)：从初始节点S开始，优先扩展最新产生的节点(最深的节点)。即：OPEN表排序策略为新产生的节点放到OPEN表的前端，优先扩展。

DFS遍历搜索算法：从初始状态顶点S出发深度优先遍历图的方法

1. 访问S——visit (S)
2. 依次从S的未被访问过的邻接点出发进行深度遍历

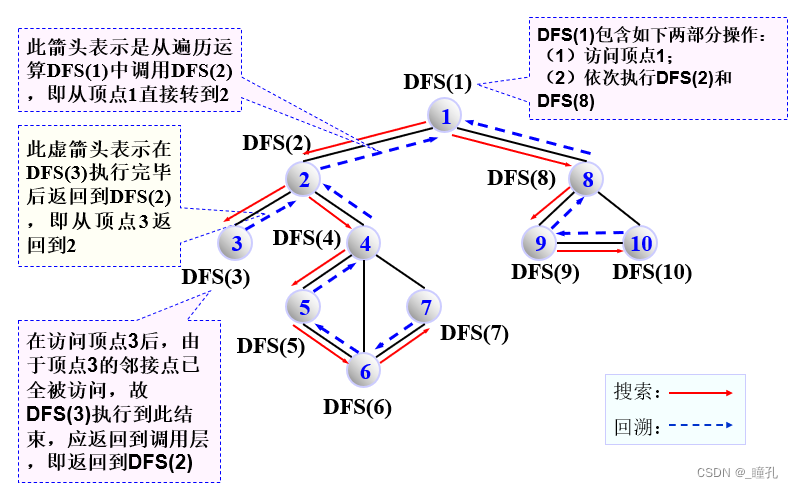
顶点访问序列为：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10

执行DFS(1)的生成树：

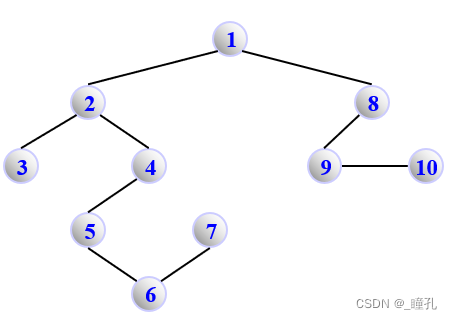
状态空间深度优先搜索：

1. 把初始节点s放入OPEN表
2. 如果OPEN表为空，则问题无解，退出
3. 把OPEN表的第一个节点(记为节点n)取出，放入CLOSED表
4. 考查节点n是否为目标节点，若是，则求得了问题的解，退出
5. 若节点n不可扩展，则转第2步
6. 扩展节点n，将其子节点放入OPEN表的首部，并为每一个子节点都配置指向父节点的指针，转第2步

DFS解决八数码问题思路：

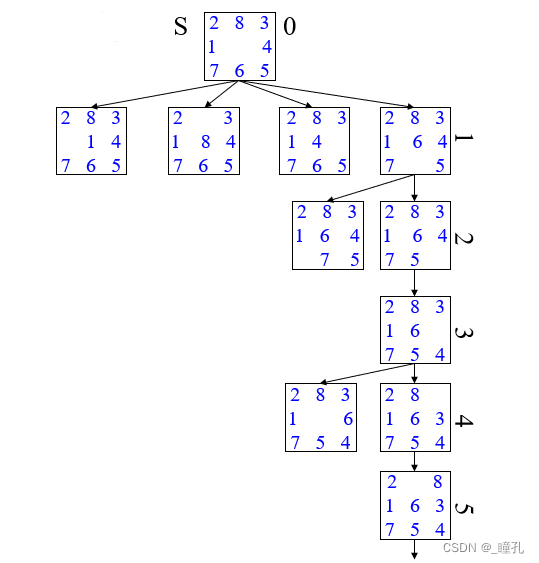
性能：

• 非完备的。如果当前搜索分支为无穷分支且无解，搜索将一直持续下去而得不到解。
• 非最优的
• 时间复杂度：O(a^b)
  • 树的分枝因子(度)：树中最大的子节点数(按最坏情况考虑)，设为a
  • 搜索深度：b
• 空间复杂度：O(a*b)

应用实例：搜索引擎中的网络爬虫——选取一个网页，选择一个超链接，进入下一个页面，选择一个超链接，再进入下一个页面，直到一个页面没有超链接，再逐层返回处理下一个超链接。

注意：

• 这里的BFS和DFS与数据结构中的算法的唯一区别是不一定要遍历所有顶点
• 这里只要到达目标顶点，算法即结束

4.3：有界深度优先搜索

在深度优先搜索中，如果进入无穷且无解分支，搜索将一直持续下去，得不到问题的解，白白浪费计算机的时间、空间资源。为了防止出现此类情况人们提出了有界深度优先搜索策略。

指定最大搜索深度dmax作为深度界限，仍按深度优先搜索方法搜索，当搜索到深度界限仍未到达目标，则视此搜索路径无解，继续搜索其他路径。

有界深度优先搜索性能同深度优先搜索。

有界深度搜索过程如下:

1. 把初始节点S放入OPEN表，置S的深度d(S)=0
2. 如果OPEN表为空，则问题无解，退出
3. 把OPEN表的第一个节点(记为节点n)取出，放入CLOSED表
4. 考查节点n是否为目标节点，若是，则求得了问题的解，退出
5. 如果节点n的深度d(节点n)=dmax。则转第2步
6. 若节点n不可扩展，则转第2步
7. 扩展节点n，将其子节点放入OPEN表的首部，并为每一个子节点都配置指向父节点的指针，转第2步

4.4：迭代加深深度优先搜索

在有界深度优先搜索中，如果深度界限设定不合适，太小则可能遗漏问题的解，太大则浪费时空资源。

迭代加深搜索中，深度界限是动态变化的，从深度为1开始，找不到目标，就把深度界限加1，重新开始深度优先搜索，直到找到解或无解为止

性能：

• 完备的
• 最优的：对于深度指标
• 时间复杂度：O(a^b)
  • 树的分枝因子(度)：树中最大的子节点数(按最坏情况考虑)设为a
  • 搜索深度：b
• 空间复杂度：O(a*b)

五：状态空间的启发式搜索

启发式搜索，又叫做有信息搜索

盲目搜索是按事先规定的路线进行搜索。这些策略搜索效率低下，浪费计算机时空资源，容易造成组合爆炸。可能丢掉最优解甚至全部解。而启发式搜索策略在搜索过程中，会针对问题自身的特性，利用问题领域的相关信息来帮助搜索，使得搜索朝着最有希望的方向前进，提高搜索效率。

5.1：启发性信息和估价函数

启发信息：关于问题领域的，用来帮助搜索的信息。

启发信息按信息用途分类：

• 用于决定下一个要扩展的节点：总是选择最有希望产生目标的节点（邻接点）优先扩展，即OPEN表按此希望值排序。这类启发信息使用最为广泛
• 用于决定产生哪些子节点：扩展一个节点时，有选择的生成子节点（选择访问邻接点)，有些明显无用或没有优势的子节点不让其产生出来
• 用于决定从搜索图中修剪或抛弃哪些节点
  • 减小待搜索空间
  • 搜索图中，不访问这些顶点，或直接删除掉这些顶点

估价函数(evaluation function)与启发函数(heuristic function)：

• 利用启发信息，构造一个函数，对搜索路径全程的代价或希望进行评估
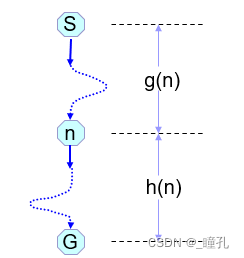
• 下右图，当前节点为n，定义估价函数f(n)：从初始节点S开始，约束通过n，到达目标节点G的全程代价的估计值。即：f(n)=g(n)+h(n)
  • g(n)为从S到n，已经走过的路径代价估计，通常即用实际花费代价，也比较容易计算
  • h(n)是从n到达目标G代价的估值，这一段路径是没有走过的，必须根据问题特性，利用启发信息进行估算。搜索的启发性即体现在h(n)上，所以把h(n)叫做启发函数

估价函数的构造对多数问题不是一件容易的事。搜索的有效性取决于估价函数的构造，不当的估价函数可能失去最优解甚至全部解。此外，构造估价函数时要考虑时空代价的折中。保证有效性的优先次序是至少保证能找到解，然后保证能获得较优解，最后是获得一个最优解。

5.2：A算法

A算法又叫最好优先搜索(Best First Search)、有序搜索(Ordered Search)。在图搜索算法中，如果能在搜索的每一步都利用估价函数f(n)=g(n)+h(n)对Open表中的节点进行排序，则该搜索算法为A算法。

A算法描述：

1. 把初始节点S放入Open表中，f(S)=g(S)+h(S)
2. 如果Open表为空，则问题无解，失败退出
3. 把Open表的第一个节点取出放入Closed表，并记该节点为n
4. 考察节点n是否为目标节点。若是，则找到了问题的解，成功退出
5. 若节点n不可扩展，则转第2步
6. 扩展节点n，生成其子节点n_i(i=1，2，…)，计算每一个子节点的估价值f(n_i)(i=1，2，…)，并为每一个子节点设置指向父节点的指针，然后将这些子节点放入Open表中
7. 根据各节点的估价A数值，对Open表中的全部节点按从小到天的顺序重新进行排序
8. 转第2步

性能：

• 完备的
• 非最优的
• 时间复杂度：O(a^b)
  • 树的分枝因子(度)：树中最大的子节点数(按最坏情况考虑)设为a
  • 搜索深度：b
• 空间复杂度：O(a^b)

例题：下图为一个城市地图，用最好优先搜索求从a城市出发到达i城市的路径。g(n)用从a城市到n城市走过的实际距离。h(n)用后面的表给出，您可以设想h(n)为n到达i的直线距离。

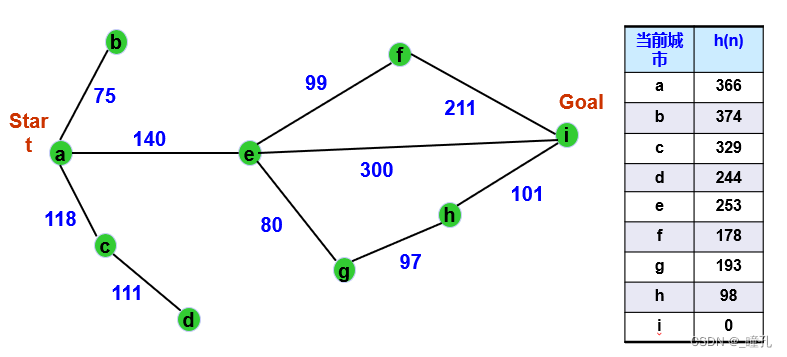
求解过程如下，用A算法求解路径为：aeghi(418)，其中，实际路径代价(距离)为418

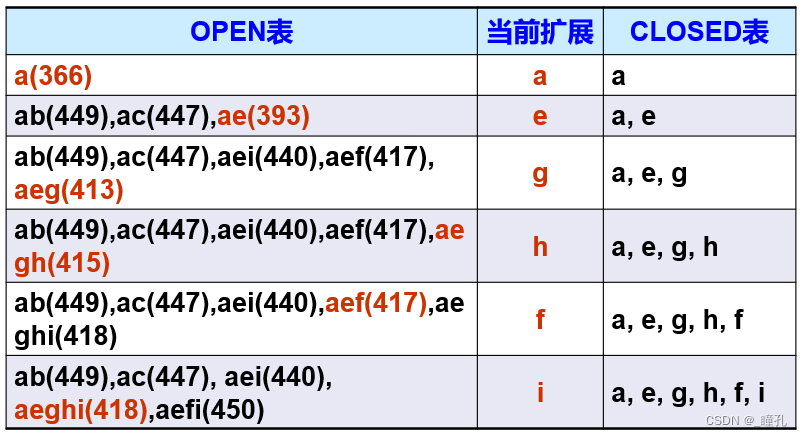
A搜索算法得到的解为aeghi，在本题中为最优解，因为本题满足了A算法的条件。但需要注意的是A算法不保证能取得全局最优解。

A算法求解八数码问题：

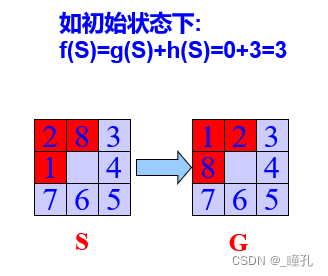
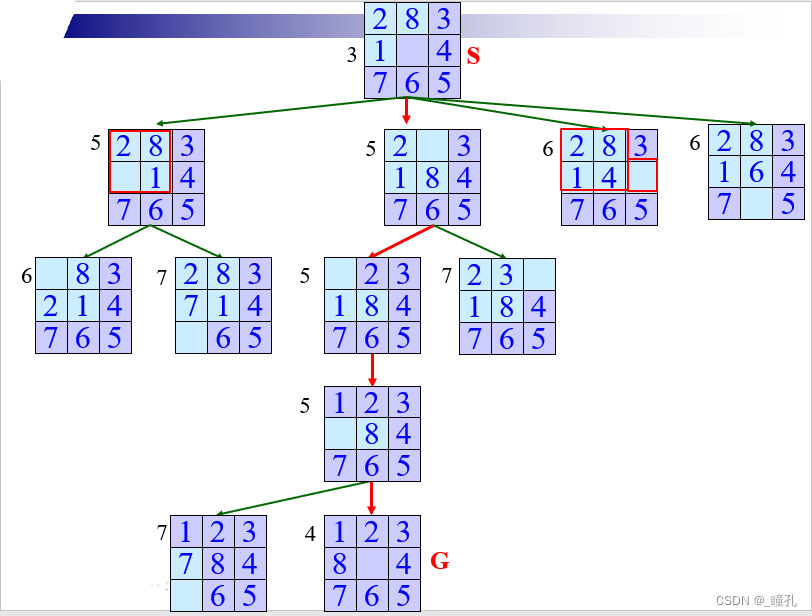
5.3：爬山搜索算法

爬山搜索是一种贪婪算法，其本质上是梯度下降法。在评估函数f(n)=g(n)+h(n)中，令g(n)=0，即f(n)=h(n)，A算法即成为爬山搜索算法。

爬山算法每次从当前的节点开始，与周围的邻接点进行比较：

• 若当前节点是最大的，那么返回当前节点，作为最大值
• 若当前节点是最小的，就用最高的邻接点替换当前节点，从而实现向山峰的高处攀爬的目的

如此循环往复，直到达到最高点为止。但该算法的主要问题是：局部最大，即某个节点会比周围任何一个邻居都高，但只是局部最优解，并非全局最优解。

如下图，在处于当前解时，爬山法搜索到局部最优解后，就会停止搜索，因为在局部最优解这个点，无论向哪个方向小幅度的移动，都无法得到更优解

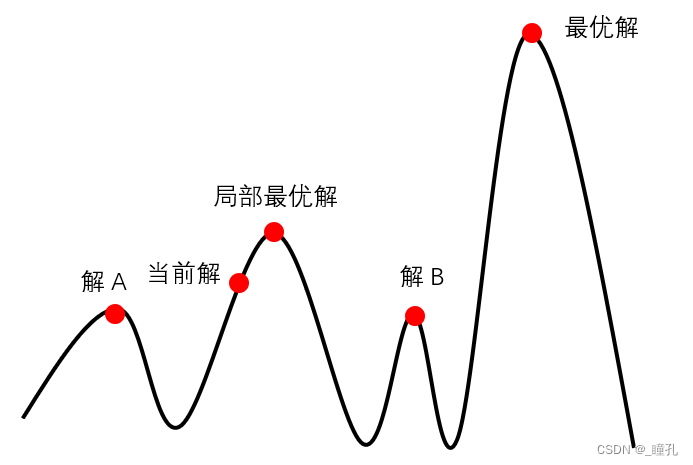
此外，其还存在以下两种问题：

• 高地问题：搜索一旦到达高地，就无法确定搜索最佳方向，会产生随机走动，使得搜索效率降低
• 山脊问题：搜索可能会在山脊的两面来回震荡，前进步伐很小

用爬山算法求解上面的TSP问题：

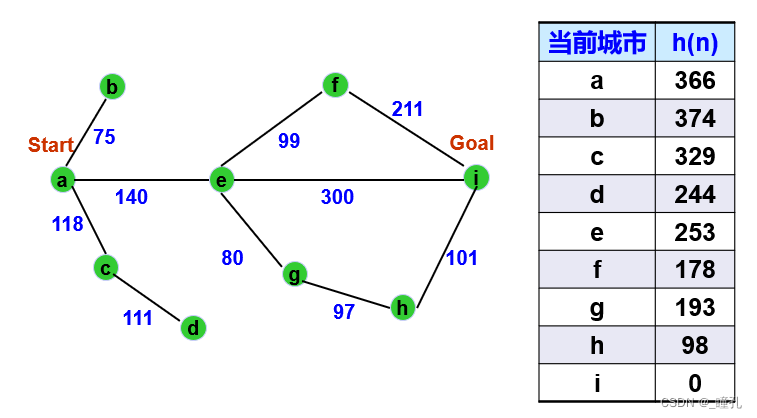
由于g(n)=0，所以解为aei：

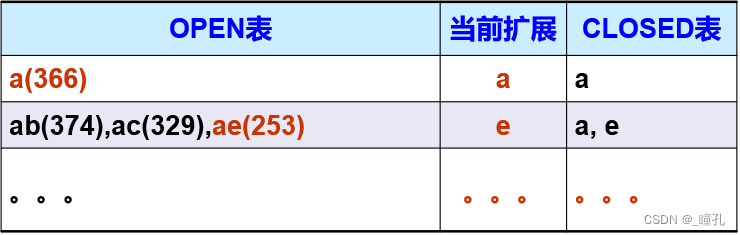
本题有3条解路径：

• aei，全程实际代价为440
• aefi，全程实际代价为450
• aeghi，全程实际代价为418

而爬山搜索得到的解为aei，可见不是全局最优解。但对比前面A算法，可见爬山搜索效率较高。

5.4：等代价搜索

等代价搜索(Uniformed-cost search)，即Dijkstra(迪杰斯特拉)算法。在评估函数f(n)=g(n)+h(n)中，令h(n)=0，f(n)=g(n)，且g(n)为实际路径代价，此时的A算法称为等代价搜索。

为什么等代价搜索属于盲目搜索：因为h(n)=0，没有了启发性，所以属于盲目搜索

性能：

• 最优性—找到全局最优解
• 完备性
• 时空复杂度同A算法
• 搜索效率低

用等代价搜索求解上述TSP问题：

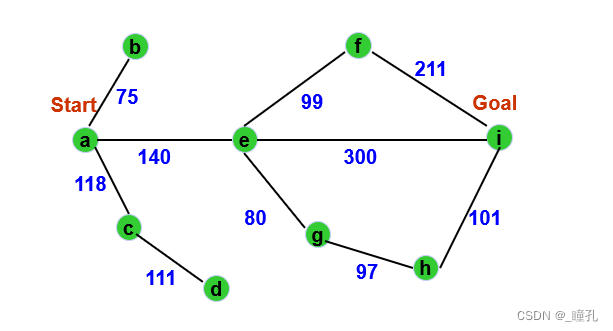
求解如下

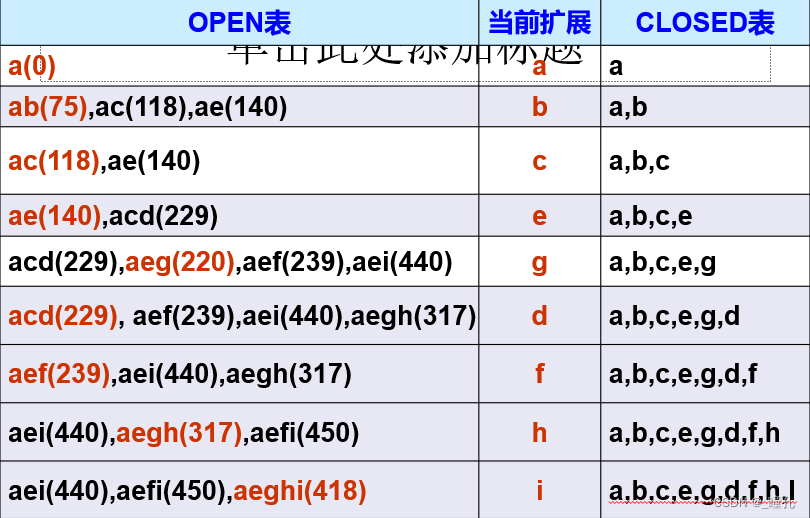
5.5：A*算法

对A算法中的评估函数加上一些限制，使为A*算法。

公式表示为： f*(n)=g*(n)+h*(n)

• f*(n) 是从初始状态经由状态n到目标状态的最小路径代价
• g*(n) 是在状态空间中从初始状态到状态n的实际代价
• h*(n) 是从状态n到目标状态的路径的最小估计代价。若有多个目标结点，取其中的最接近值

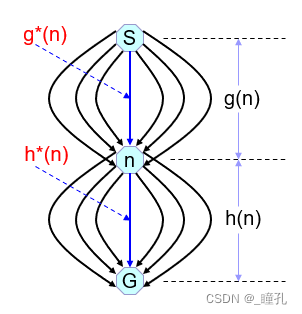
当A算法的评估函数f(n)=g(n)+h(n)满足以下条件，即为A*算法：

• g(n) >= g*(n) && g(n) > 0
• h(n) <= h*(n)

实际使用时，常使g(n)=g*(n)，即从S到n的实际最小代价

• g(n)表示从点S到达节点n的当前最小代价
• g*(n)表示从节点S到节点n的实际最小代价
• h(n)表示从节点n到目标节点G的预估代价
• h*(n)表示从节点n到目标节点G的实际最小代价

真实h(n)的选取：保证找到最短路径（最优解的）条件，关键在于估价函数f(n)的选取（或者说h(n)的选取）。
以h(n)表达状态n到目标状态估计的距离，那么h(n)的选取大致有如下情况：

• 在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。
• 如果h(n)始终小于等于h*(n)，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
• 如果h(n)完全等于h*(n)，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
• 如果h(n)的值比h*(n)大，则A*算法不能保证找到最短路径，不过此时会很快。
• 在另外一个极端情况下，如果h(n)相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

A*算法的特点：

• 最优性：保证最优解存在时能找到最优解
• 可采纳性：算法能在有限步内终止，并能找到最优解

5.6：f(n)=g(n)+h(n)讨论

• f(n)=g(n)，h(n)=0，g(n)为实际路径代价：等代价搜索——效率不高，能得到最优解
• f(n)=h(n)，g(n)=0，爬山搜索——效率极高，往往陷入局部最优
• f(n)=g(n)+h(n)，g(n)>0，h(n)>0，最好优先搜索——但是设计估价函数时要充分考虑g(n)和h(n)的数量级要相当。否则当g(n)>>h(n)时，接近等代价搜索；h(n)>>g(n)时，接近爬山搜索
• f(n)=g(n)+h(n)，g(n)>0，且g(n)>=g*(n)，h(n)<=h*(n)，A*算法——为了兼顾搜索效率，在满足上述条件前提下，要尽可能取较大的h(n)值，尽可能提高搜索效率
• f(n)=0，即g(n)=0，h(n)=0，盲目搜索