8本电子书免费送给大家，见文末。

1、DeBERTa与BERT的区别

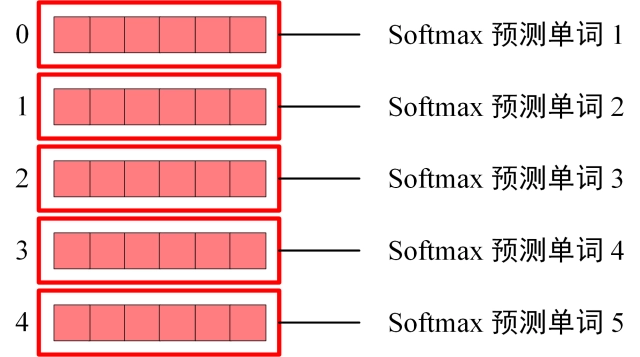
DeBERTa提出了两种改进BERT预训练的方法：第一种方法是分散注意机制，该机制使用两个向量分别对每个单词的内容和位置进行编码来表示每个单词，并使用分散矩阵计算单词之间在内容和相对位置上的注意力权重；第二个方法是一个增强的掩码解码器，它取代了输出的Softmax层来预测用于MLM预训练的掩码令牌。使用这两种技术，新的预训练语言模型DeBERTa在许多下游NLP任务上表现都优于RoBERTa和BERT。

2、逻辑回归损失，参数更新公式

逻辑回归损失函数如下：

J(θ)=−1m∑i=1m[y(i)ln⁡(hθ(x(i)))+(1−y(i))ln⁡(1−hθ(x(i)))]

求梯度如下：

∂J(θ)∂θj=1m∑i=1m[hθ(x(i))−y(i)]⋅xj(i)

参数更新如下：

θj=θj−α⋅∂J(θ)∂θj=θj−α⋅1m∑i=1m[hθ(x(i))−y(i)]xj(i)

3、线性回归损失，参数更新公式

线性回归损失如下：

J(w,b)=12m∑i=1m(h(x(i))−y(i))2

求梯度如下：

∂∂wjJ(w,b)=1m∑i=1m(h(xi)−y(i))xj(i)∂∂bJ(w,b)=1m∑i=1m(h(xi)−y(i))

参数更新公式如下：

wj:=wj−α1m∑i=1m(h(x(i))−y(i))xj(i)b:=b−α1m∑i=1m(h(x(i))−y(i))

4、多分类任务如何去做

1）将多分类任务拆成多个二分类任务

• 一对一(One vs One)：将N个类别两两配对，从而产生N(N-1)/2个分类任务:
• 一对其余(One vs Rest)：每次将一个类的样例作为正例，其他类的样例作为反例来训练N个分类器；
• 多对多(Many vs Many)：每次将若干个类作为正类，若干个其他类作为反类。

2）多分类模型直接实现多分类

直接采用现有的多分类模型如LightGBM或者深度模型神经网络进行多分类。

5、Leetcode：第K大的数

两种方法：快排和堆排序

快排

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        def findTopKth(low, high):
            pivot = random.randint(low, high)
            nums[low], nums[pivot] = nums[pivot], nums[low]
            base = nums[low]
            i = low
            j = low + 1
            while j <= high:
                if nums[j] > base:
                    nums[i + 1], nums[j] = nums[j], nums[i + 1]
                    i += 1
                j += 1
            nums[low], nums[i] = nums[i], nums[low]
            if i == k - 1:
                return nums[i]
            elif i > k - 1:
                return findTopKth(low, i - 1)
            else:
                return findTopKth(i + 1, high)
        return findTopKth(0, len(nums) - 1)

时间复杂度为：O(n)

堆排序：

class Solution(object):
    def findKthLargest(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        heap = []
        for num in nums:
            heapq.heappush(heap, num)
            if len(heap) > k:
                heapq.heappop(heap)
        return heap[0]

时间复杂度为O(nlogk)

↓ ↓ ↓以下8本书电子版免费领，直接送 ，想要哪本评论区说声，我小窗给你↓ ↓ ↓