上一篇请移步【1】Anaconda基本命令以及相关工具:jupyter、numpy、Matplotilb_水w的博客-CSDN博客
目录
3 Numpy数组基础索引:索引和切片
◼ 基础索引
4 Numpy非常重要的数组合并与拆分操作
◼ 数组的合并-concatenate、vstack、hstack
numpy.vstack(tup)
numpy.hstack(tup)
◼ 数组的拆分-split、vsplit、hsplit
5 Numpy数组的矩阵运算
◼ Numpy的矩阵运算有何不同
◼ 一元运算
◼ 二元运算
◼ 矩阵运算
6 Numpy数组的统计运算
7 Numpy数组arg运算和排序
◼ 最大值 最小值
◼ 排序
8 Numpy数组神奇索引和布尔索引
◼ 神奇索引
◼ 布尔索引
3 Numpy数组基础索引:索引和切片
- numpy的切片操作,一般结构如num[a:b,c:d],分析时以逗号为分隔符,
- 逗号之前为要取的num行的下标范围(a到b-1),逗号之后为要取的num列的下标范围(c到d-1);
- 前面是行索引,后面是列索引。
- 如果是这种num[:b,c:d],a的值未指定,那么a为最小值0;
- 如果是这种num[a:,c:d],b的值未指定,那么b为最大值;c、d的情况同理可得。
◼ 基础索引
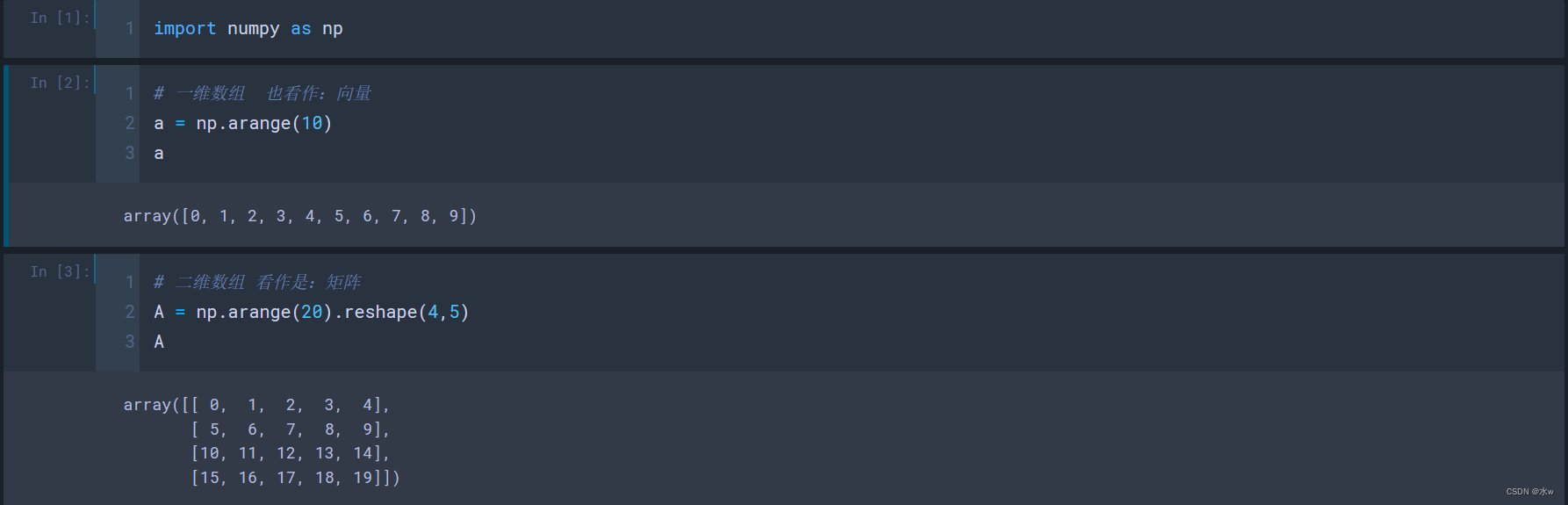
(1)对于一维数组
# 索引
a[0] # 取a中的第1个元素
a[4] # 取a中的第5个元素
a[-1] # 取a中的最后1个元素
# 切片
a[0:5] # 取a中的第1~5个元素
a[:5]
a[4:] # 取a中的第5个一直到最后的所有元素
a[-3:] # 取a中的从倒数第3个开始一直到最后的所有元素
a[:] # 取a中的所有元素
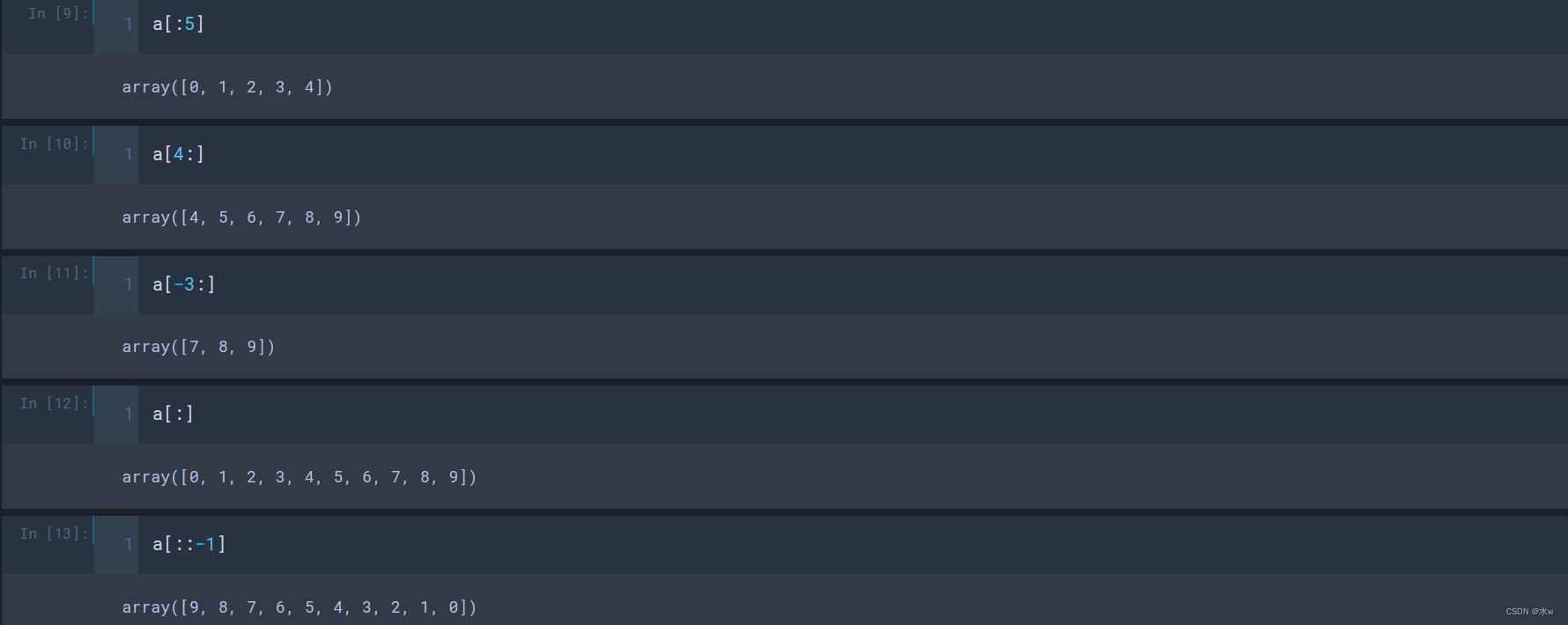
a[::2] # 取a中的所有元素,间隔步长为2
a[::-1] # 倒序取a中的所有元素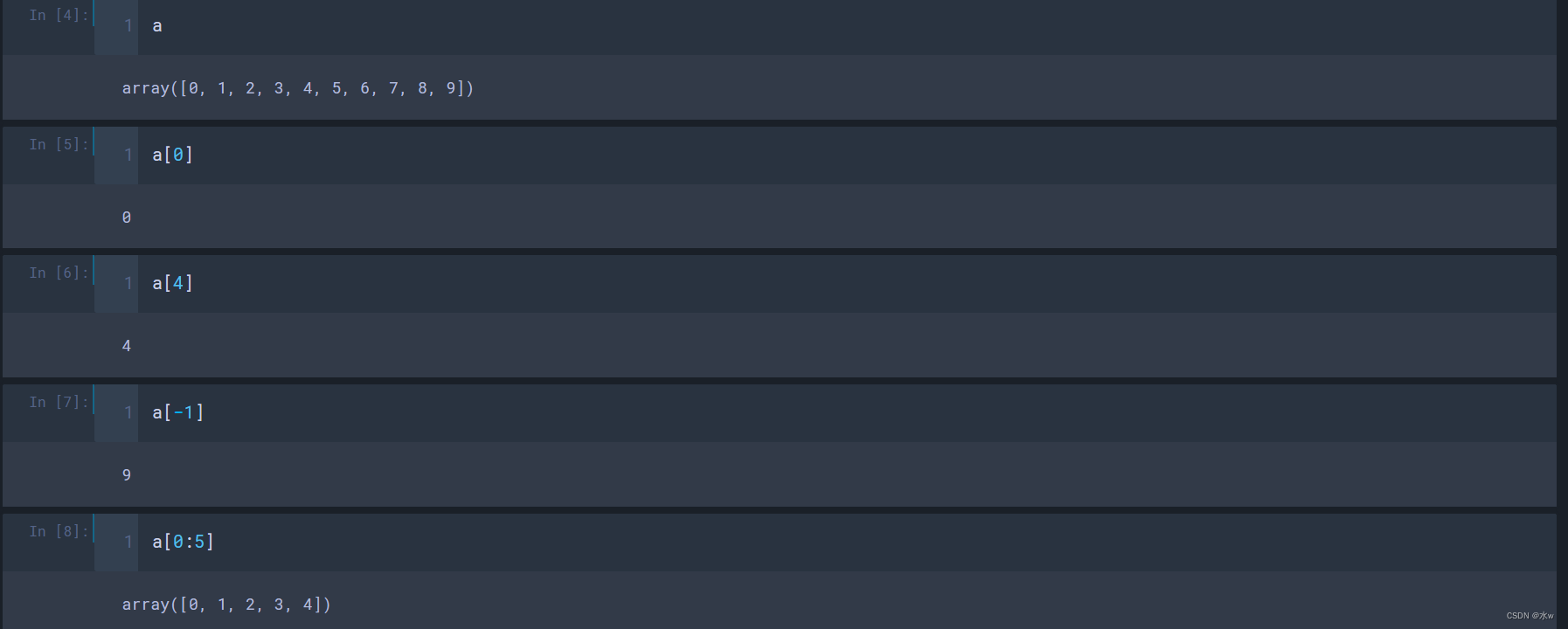
(2)对于二维数组
A[0,0] # 取A中的第1行1列的元素
A[0,:] # 取A中的第1行的所有元素
A[0]
A[-1] # 取A中的最后1行的所有元素
A[:,0] # 取A中的第1列的所有元素
A[:,-1] # 取A中的最后1列的所有元素
A[:2,:4] # 取A中的前2行前4列的所有元素
A[::-1,::-1] # 取A中所有行和列倒序的所有元素

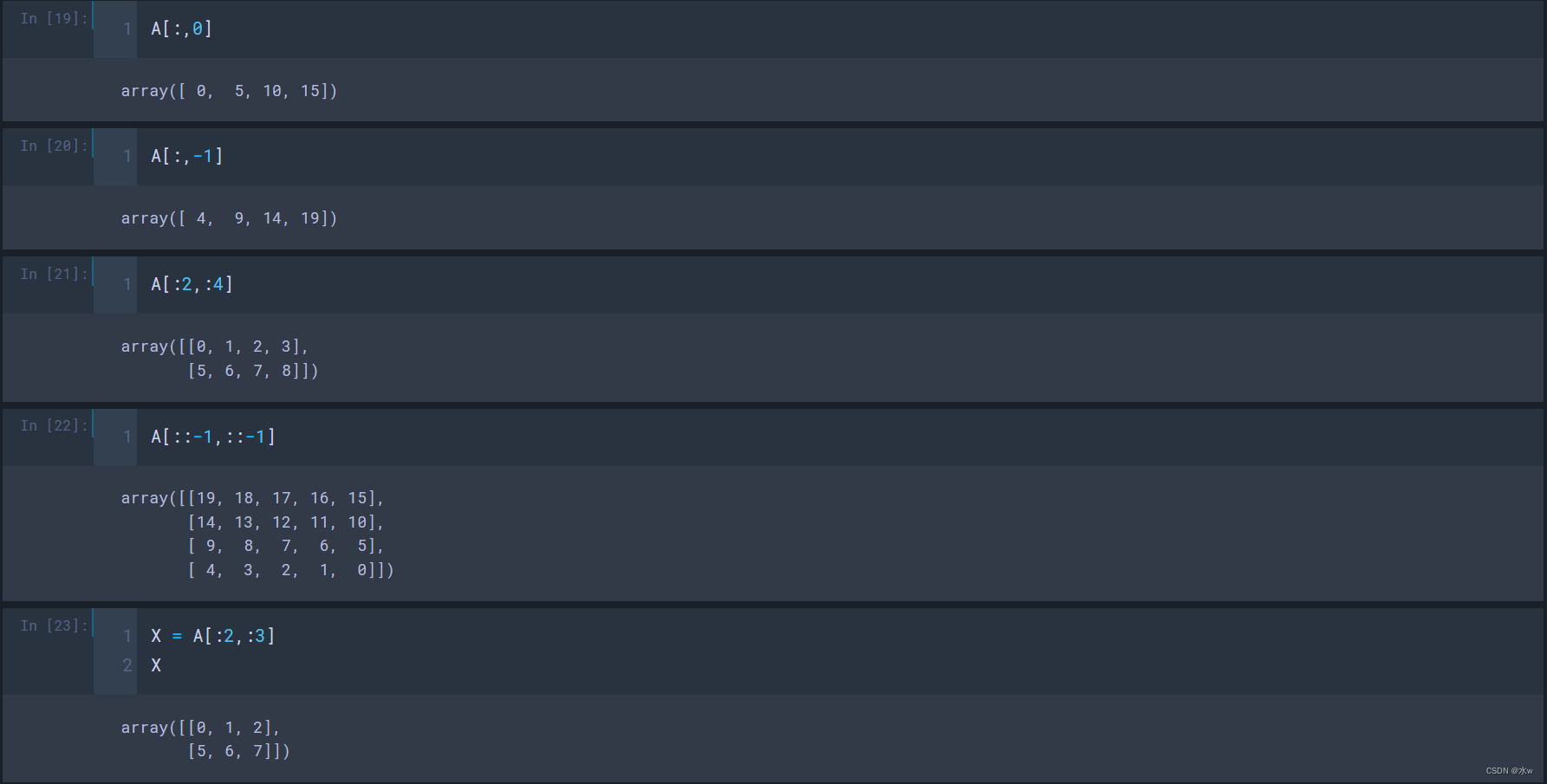
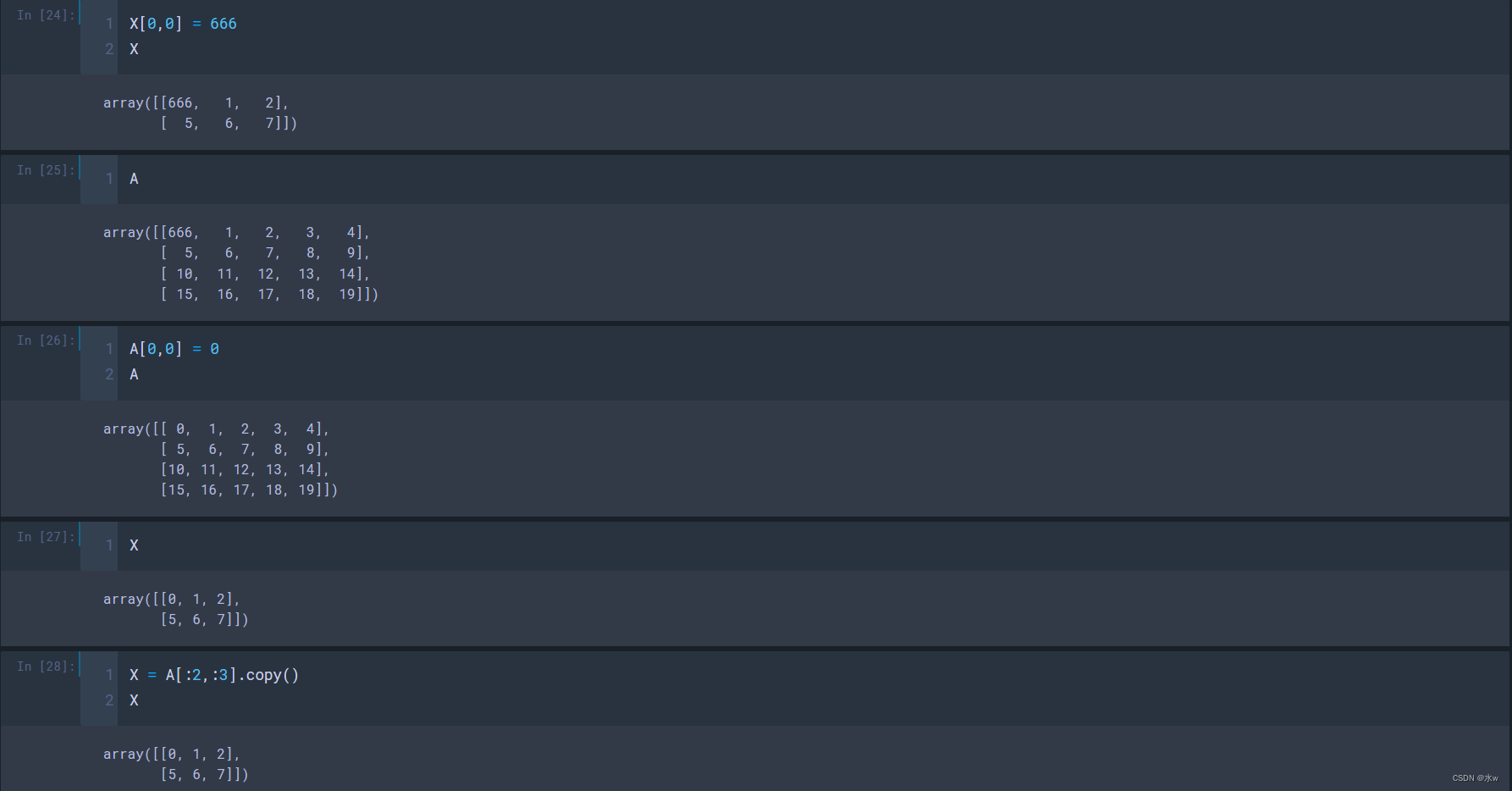
在numpy使用切片的时候要注意,numpy切片的值修改会导致原数组的值也会修改。
X = A[:2,:3] # 与原数组A有了关联关系
X[0,0] = 666
X
A
# 输出结果:
array([[666, 1, 2],
[ 5, 6, 7]])
array([[666, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14],
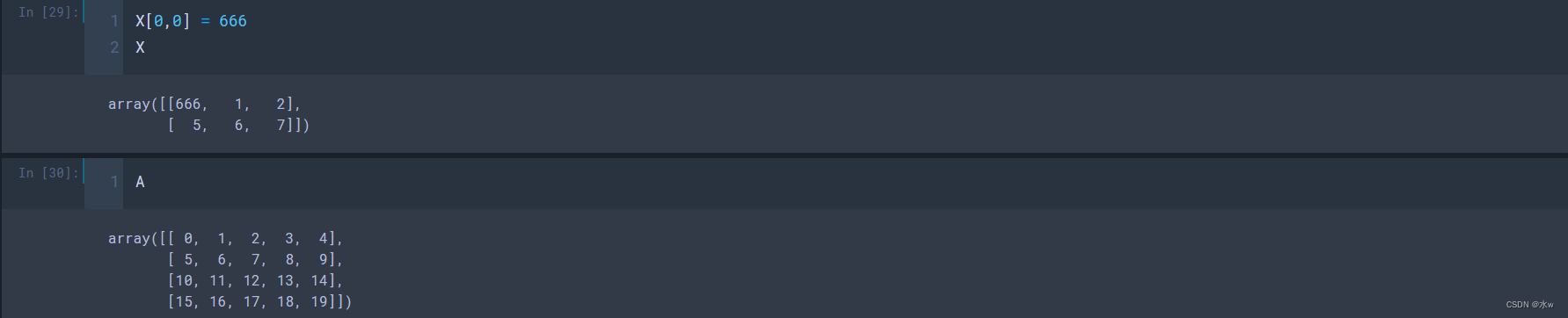
[ 15, 16, 17, 18, 19]])如果想避免这种情况,我们可以使用copy() 。
X = A[:2,:3].copy() # 相当于复制了一个新的数组,与原数组A没有了关联关系
X[0,0] = 666
X
A
# 输出结果:
array([[666, 1, 2],
[ 5, 6, 7]])
array([[0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14],
[ 15, 16, 17, 18, 19]])4 Numpy非常重要的数组合并与拆分操作
◼ 数组的合并-concatenate、vstack、hstack
numpy.concatenate((a1, a2, ...), axis=0, out=None, dtype=None, casting="same_kind")
参数:
- a1, a2, ...:sequence of array_like,除了将被对应的轴之外,数组必须是相同的形状;
- axis:int, optional,将被组合的轴,默认为0,如果为None,将被展开为一维数组;
- out:ndarray, optional,如果给定,将存放结果,尺寸必须匹配;
- dtype:str or dtype,给定输出的数据类型,不能和参数 out 一起出现;
- casting:{‘no’, ‘equiv’, ‘safe’, ‘same_kind’, ‘unsafe’}, optional,控制可能发生的数据转换类型。默认为 ‘same_kind’
结果: res是组合后的数组;
(1)合并X和a的时候,需要先让X和a有相同的维度,
np.concatenate((X,a.reshape(1,4)))
这时的X和a本身是没有任何改变的。
(2)如果想得到合并值的数组,只需要把合并结果赋值给变量,

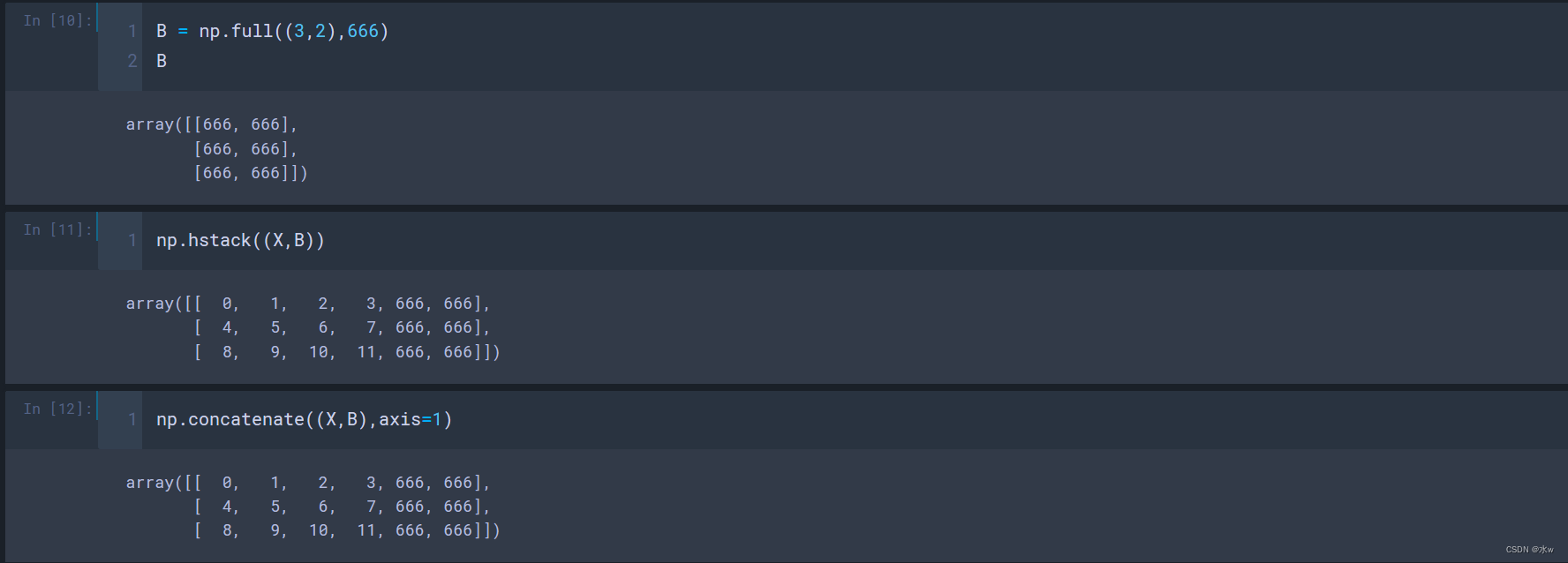
numpy.vstack(tup)参数:
tup:sequence of arrays,数组除第一维外,形状相同;结果:
stacked:ndarray,竖直(行)顺序堆叠数组,将给定的数组连接的数组;

numpy.hstack(tup)参数:
tup:sequence of arrays,数组除第二维外,形状相同;结果:
stacked:ndarray,水平(按列)顺序堆叠数组,将给定的数组连接的数组;
与np.concatenate((X,B),axis=1)的功能是相同的,
◼ 数组的拆分-split、vsplit、hsplit
numpy.split(ary, indices_or_sections, axis=0)
参数:
- ary:ndarray,被划分的数组;
- indices_or_sections:int or 1-D array,如果是 int,将被划分为N个对应维度等长的数组,如果是 1-D array,表示数组的拆分位置;
- axis:int, optional,拆分的维度,默认0;
返回:
- sub-arrays:list of ndarrays,数组 ary 的子数组视图的列表;
(1)把数组X的最后一行的元素拆分出来,
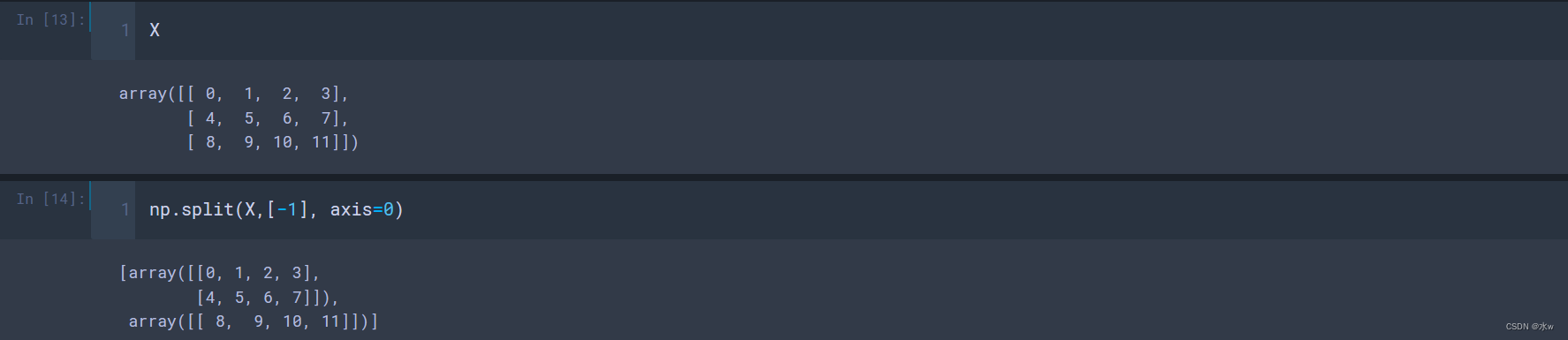
(2)把数组X的最后一列的元素拆分出来,
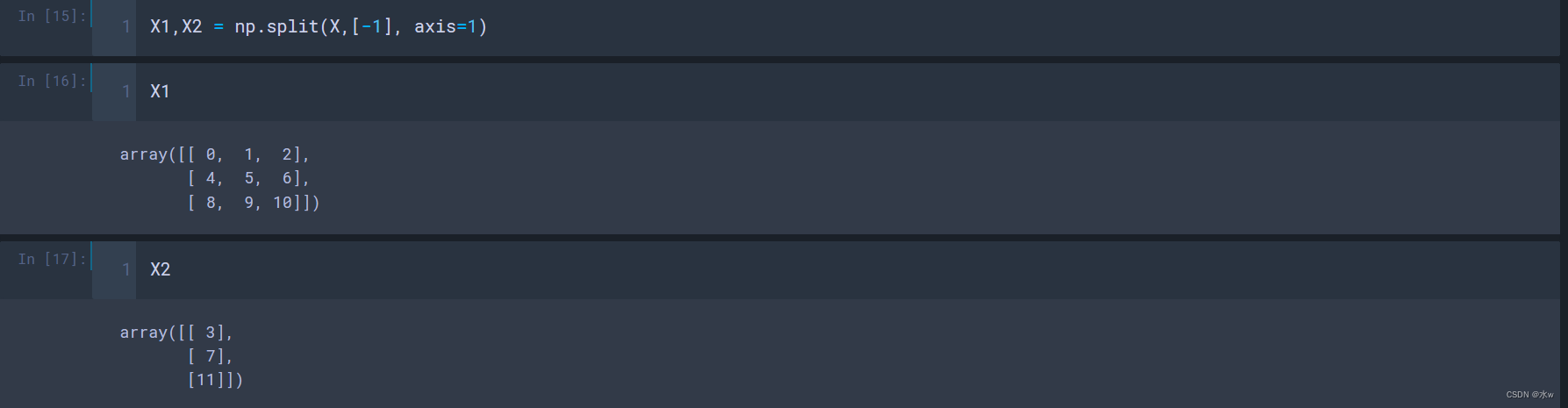
numpy.vsplit(ary, indices_or_sections)
参数:
- ary:ndarray,被划分的数组;
- indices_or_sections:int or 1-D array,如果是 int,将被划分为N个对应维度等长的数组,如果是 1-D array,表示数组的拆分位置;
返回:
- sub-arrays:list of ndarrays,竖直方向上的拆分(拆分成上下的几个数组), 数组 ary 的子数组视图的列表;

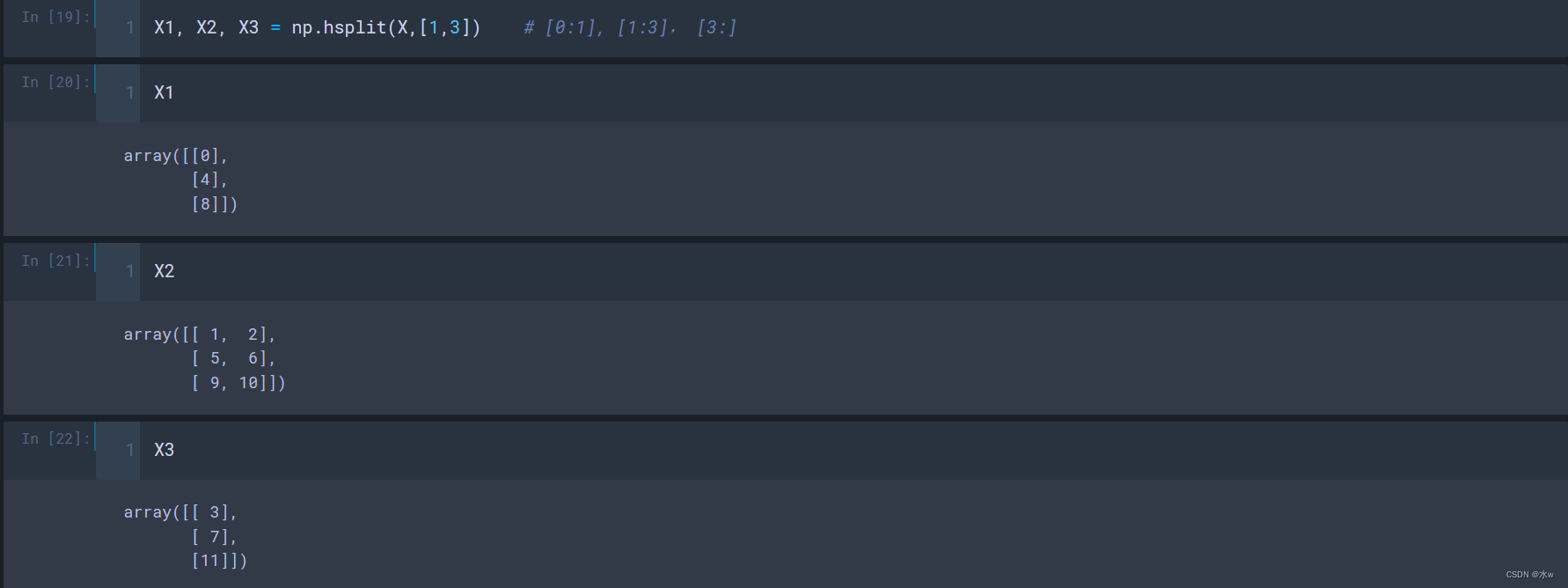
numpy.hsplit(ary, indices_or_sections)
参数:
- ary:ndarray,被划分的数组;
- indices_or_sections:int or 1-D array,如果是 int,将被划分为N个对应维度等长的数组,如果是 1-D array,表示数组的拆分位置;
返回:
- sub-arrays:list of ndarrays,水平方向上的拆分(拆分成左右的几个数组), 数组 ary 的子数组视图的列表;
5 Numpy数组的矩阵运算
◼ Numpy的矩阵运算有何不同
(1)普通数组的矩阵运算不能直接乘以2和两个X相加,需要遍历X,将每个元素乘以2,
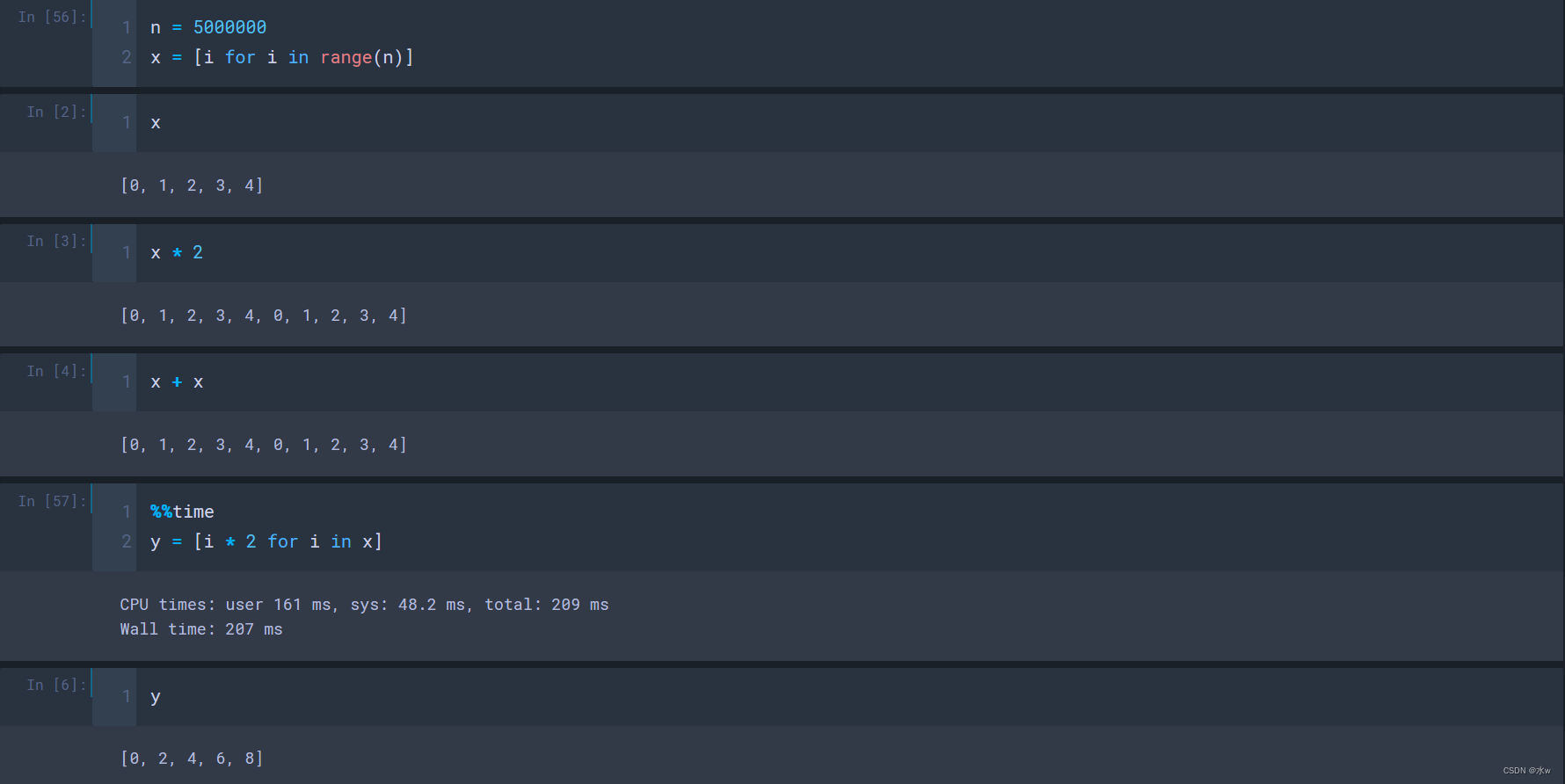
(2)而在numpy数组的矩阵运算中,可以直接乘以2,

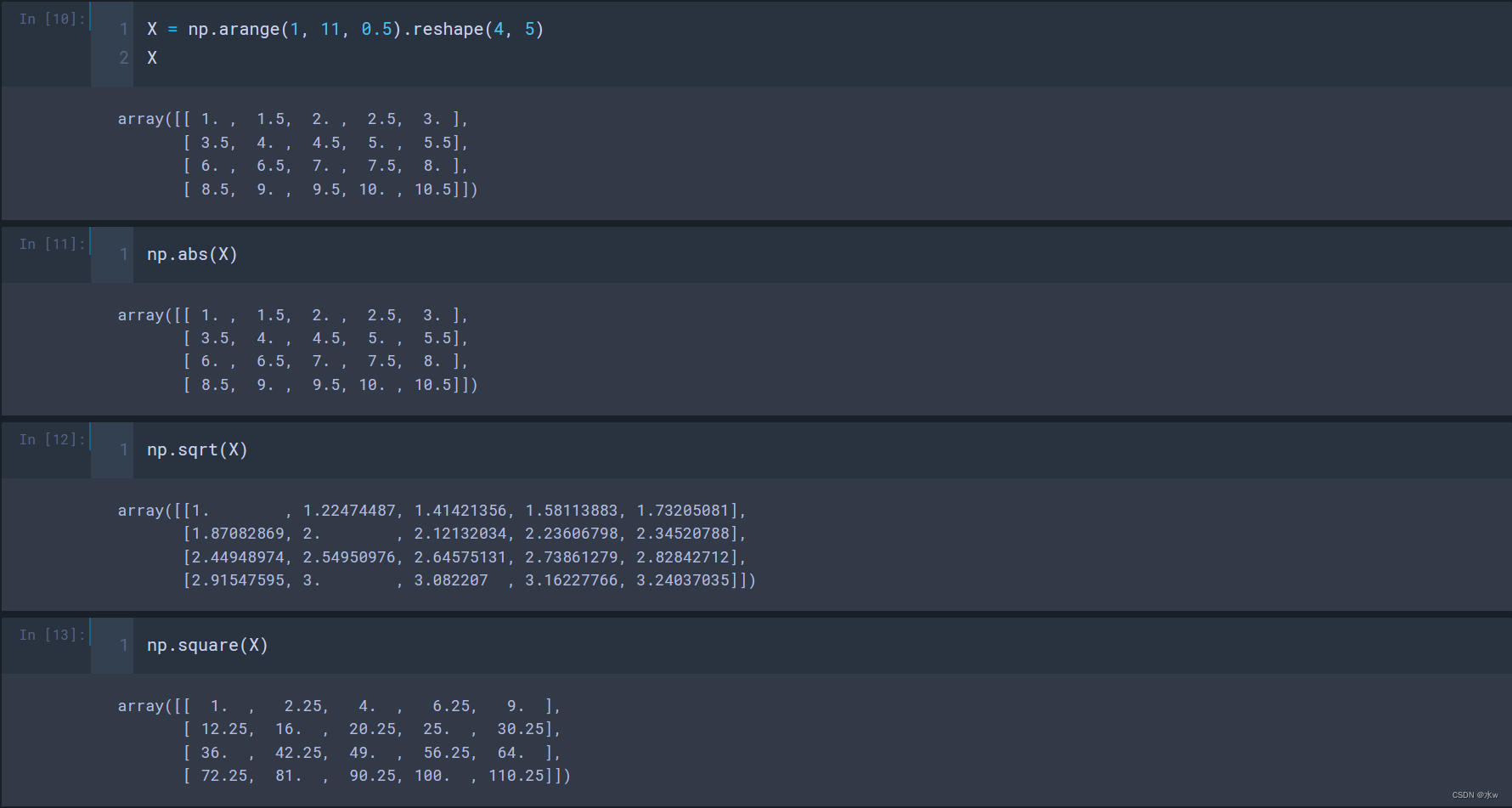
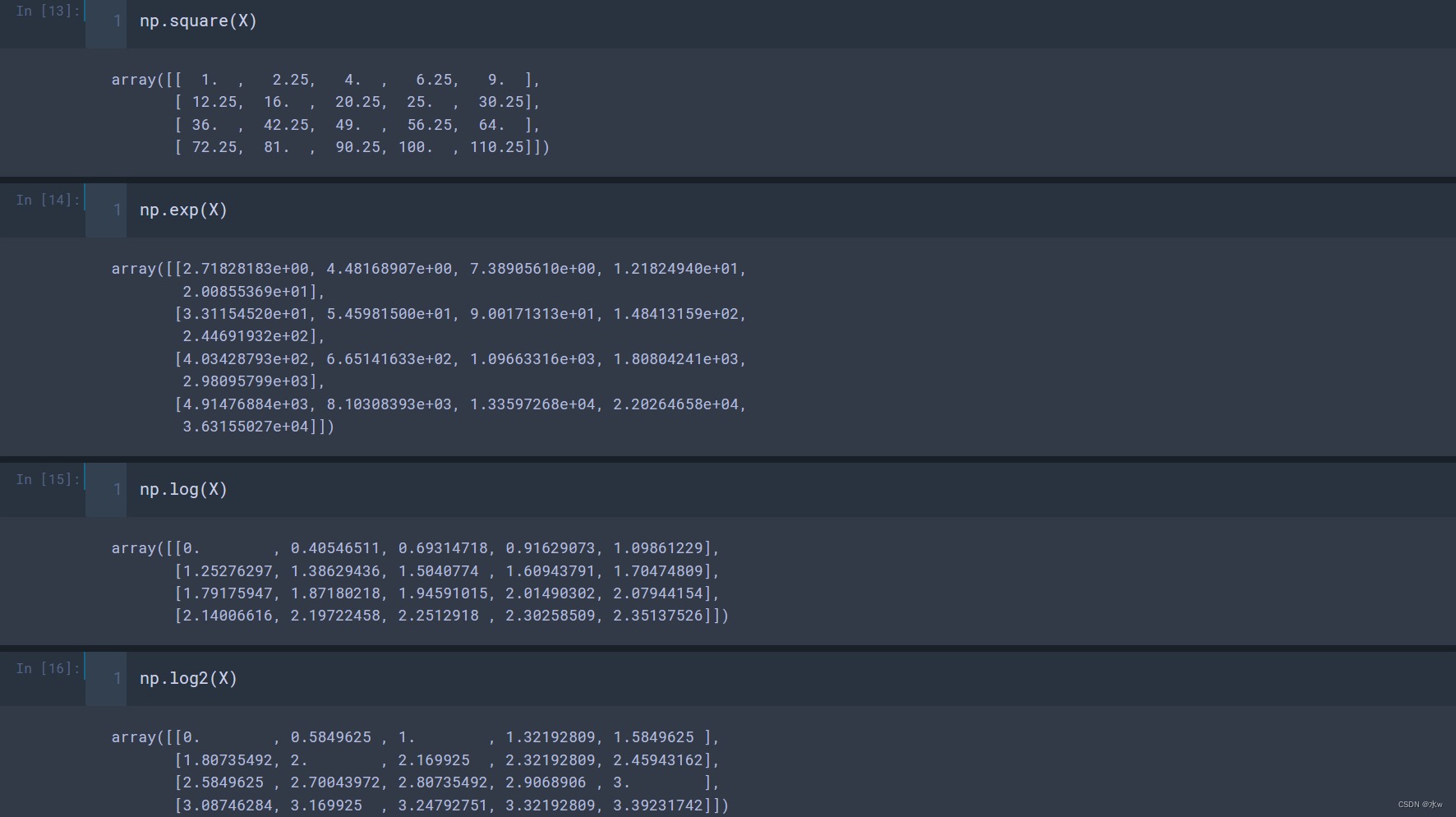
◼ 一元运算
- np.abs(a) 、np.fabs(a) : 取各元素的绝对值;
- np.sign(a) : 计算各元素的符号值 1(+),0,-1(-);
- np.sqrt(a) : 计算各元素的平方根;
- np.square(a): 计算各元素的平方;
- np.log(a) 、np.log10(a) 、np.log2(a) : 计算各元素的以自然对数e、10、2为底的对数np.exp(a) : 计算各元素的指数运算;
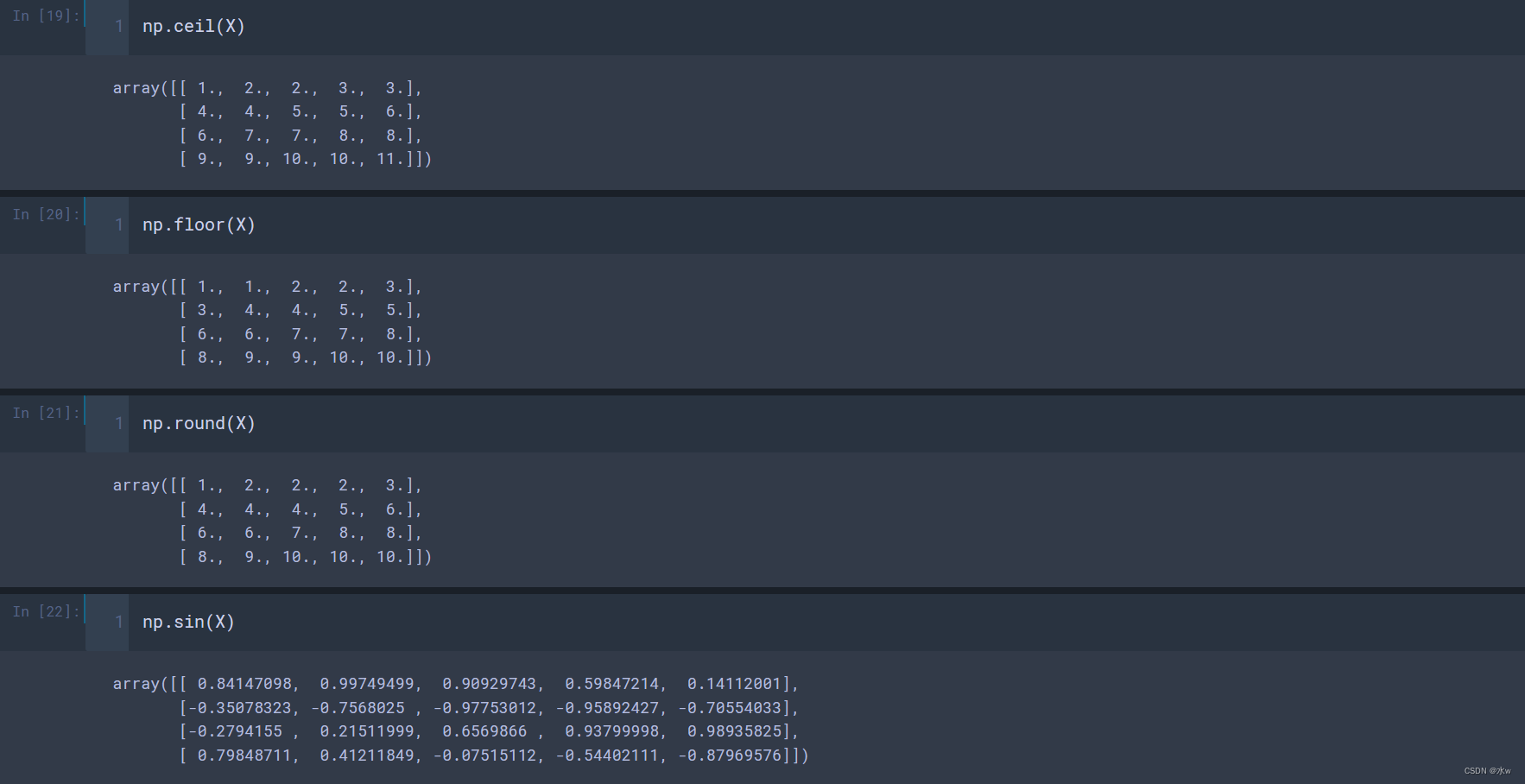
- np.ceil(a) 、np.floor(a) : 计算各元素的ceiling 值, floor值(ceiling向上取整,floor向下取整);
- np.round(a) : 各元素四舍五入,奇进偶不进(1.5进为2,但2.5不进);
- np.sin(a)、np.cos(a)、np.tan(a):三角函数;
- np.modf(a) : 将数组各元素的小数和整数部分以两个独立数组形式返回;

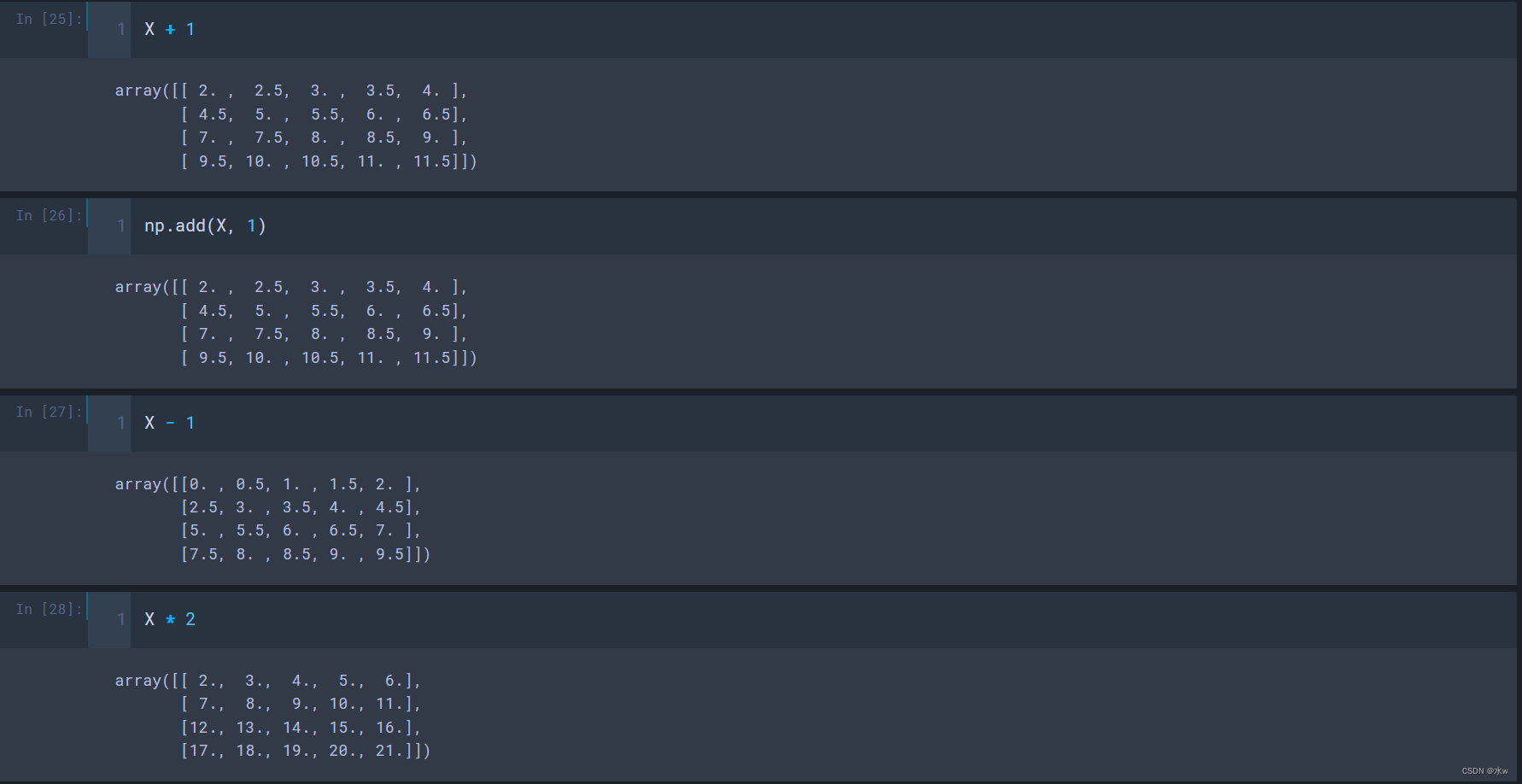
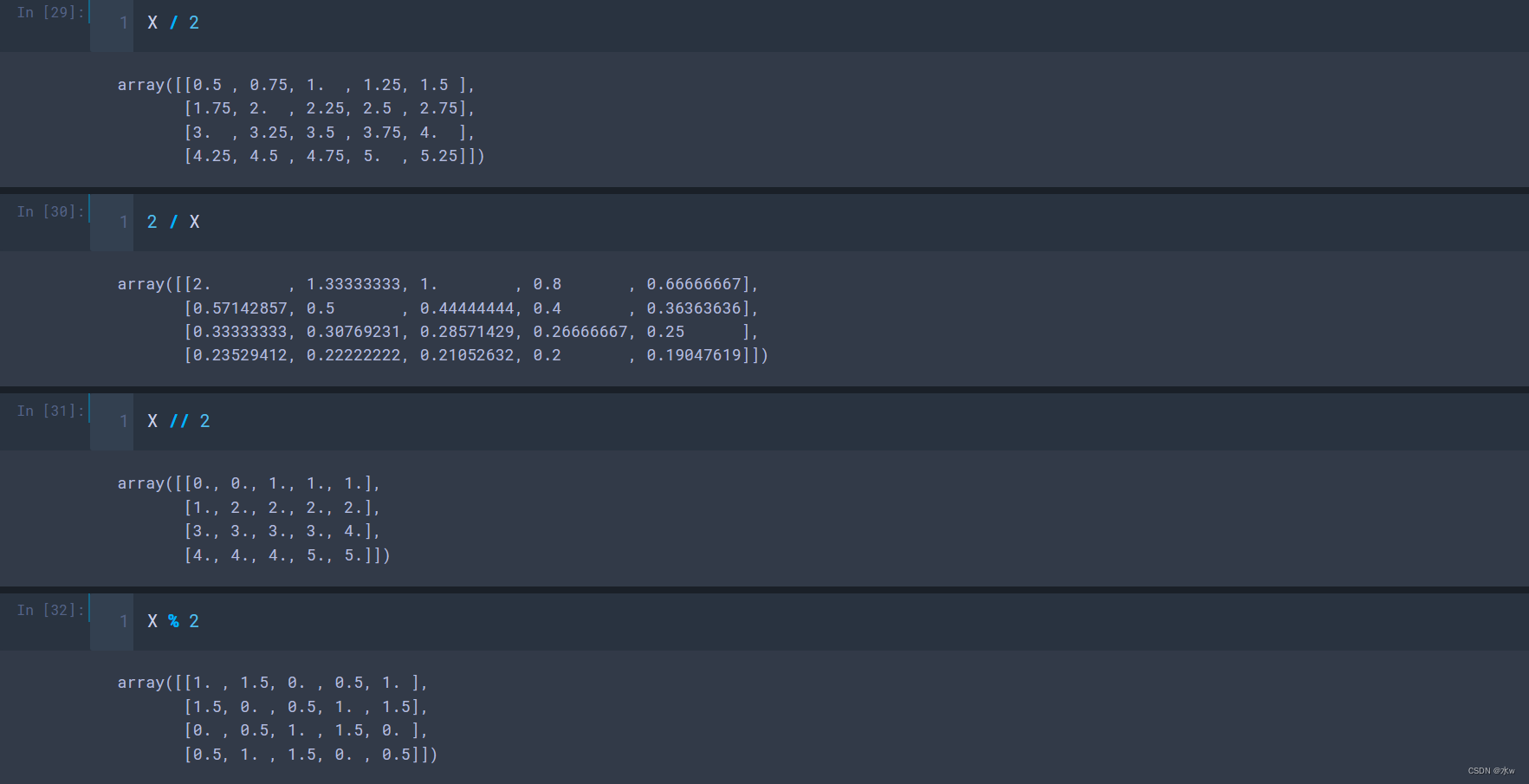
◼ 二元运算
- +、-、/、*
- //:整除;
- %:取余;
- **:幂运算;

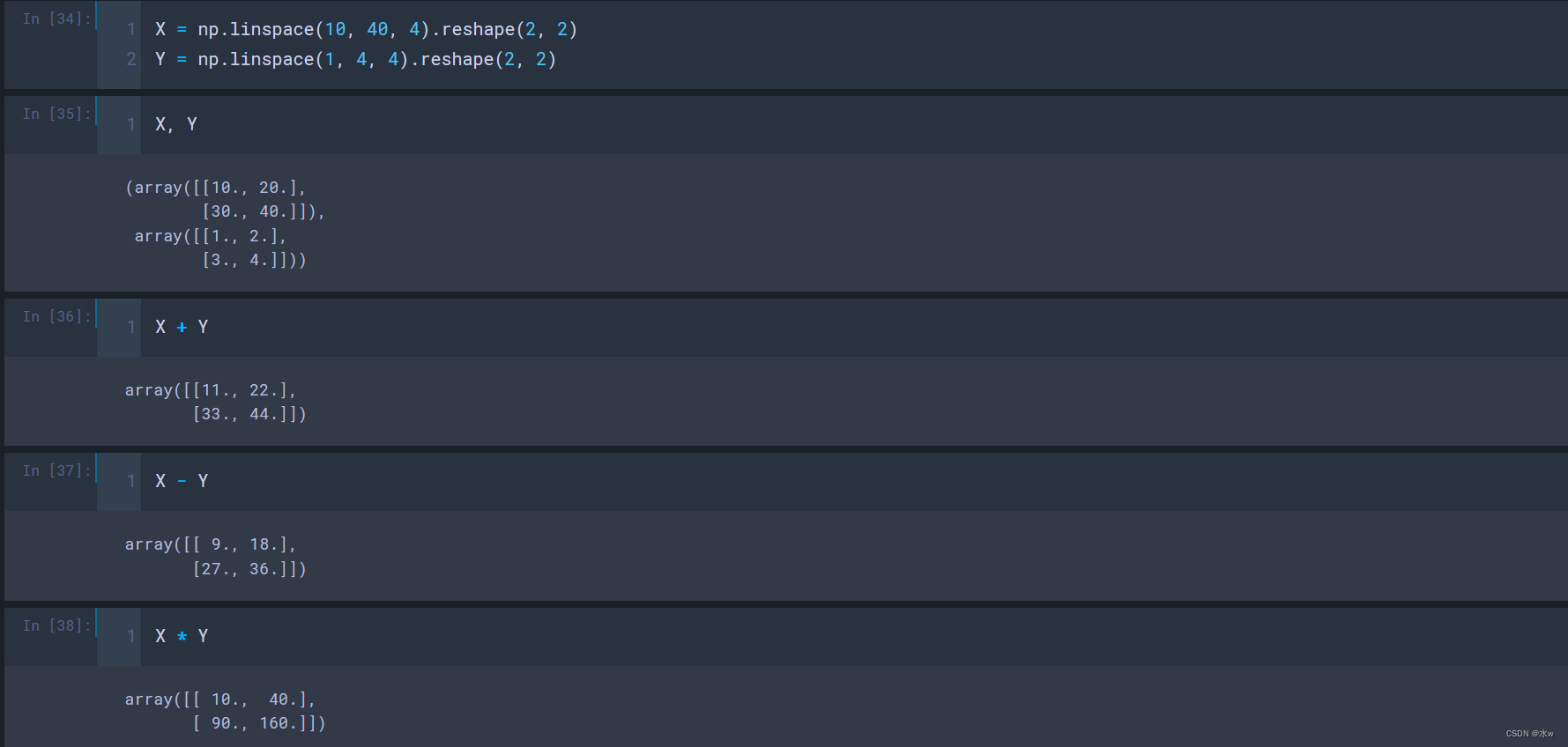
◼ 矩阵运算
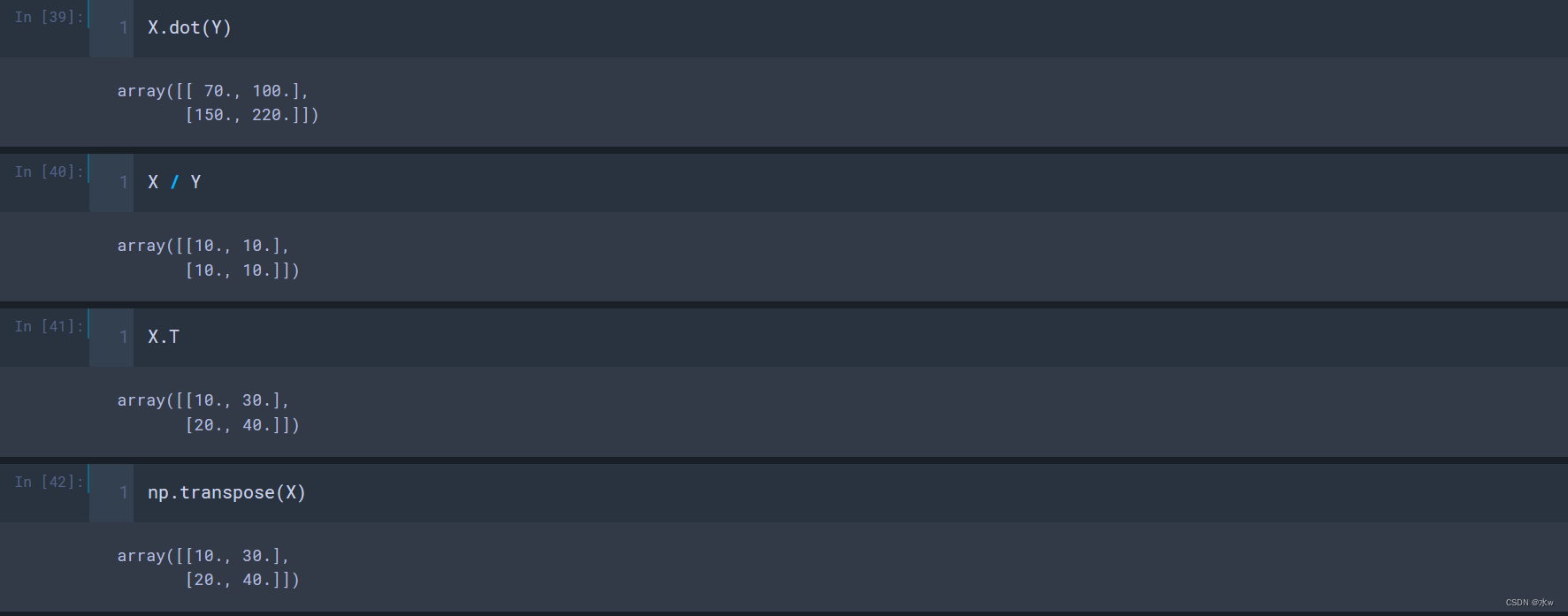
- +、-、/、*:相加、相减、相除、不是真正意义上的相乘
- dot():真正意义上的相乘;
- .T、transpose():转置;
- linspace():;
- ():;
(1)
 (2)定义的数组Z是1x2,但是数组X为2x2,此时竟然可以进行矩阵运算,
(2)定义的数组Z是1x2,但是数组X为2x2,此时竟然可以进行矩阵运算,
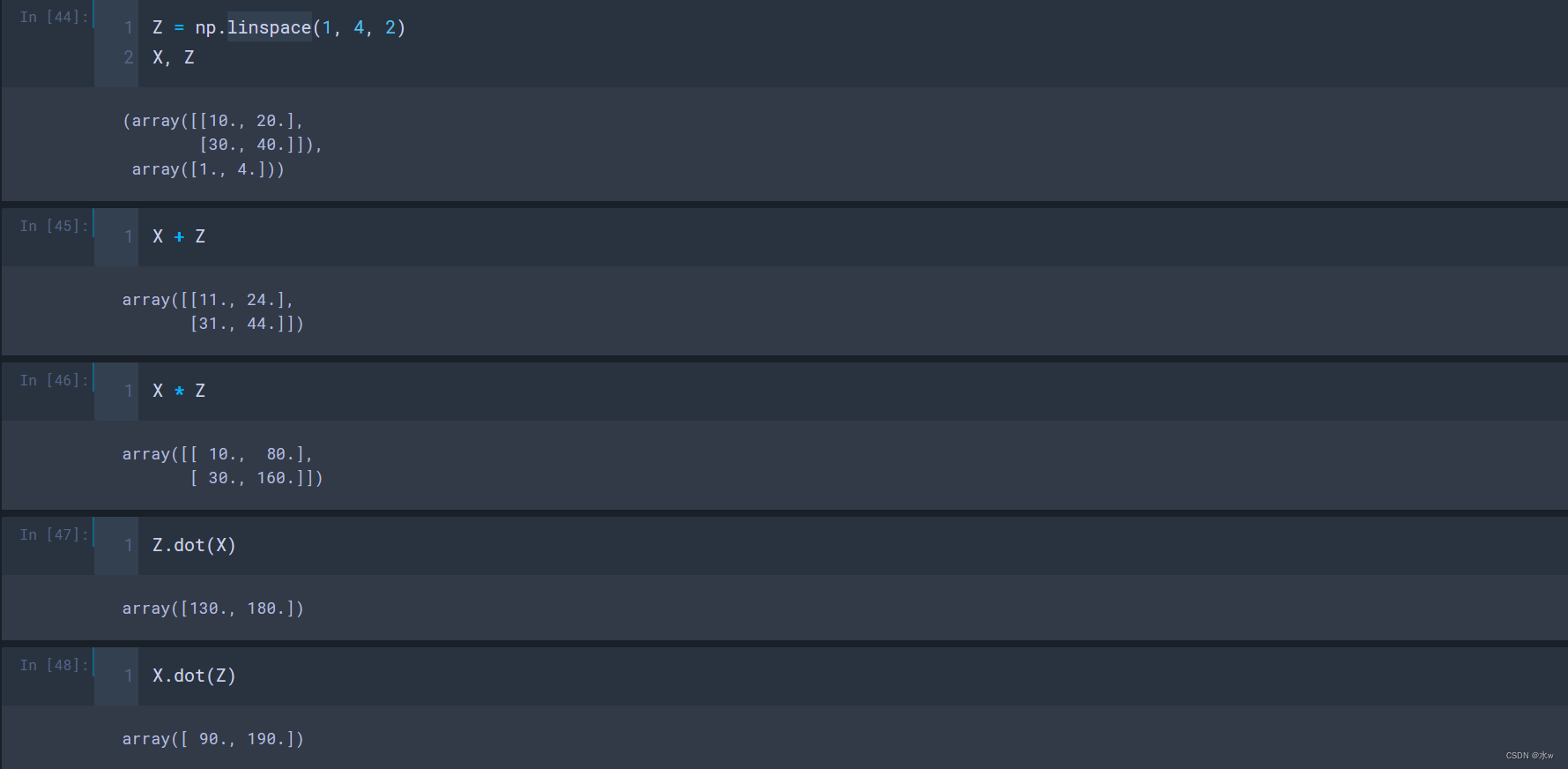
虽然numpy可以智能的通过广播的这种形式来进行运算,但事实上并不推荐,因为容易引起混乱。在矩阵运算的过程中,我们尽量还是遵从运算的规律。
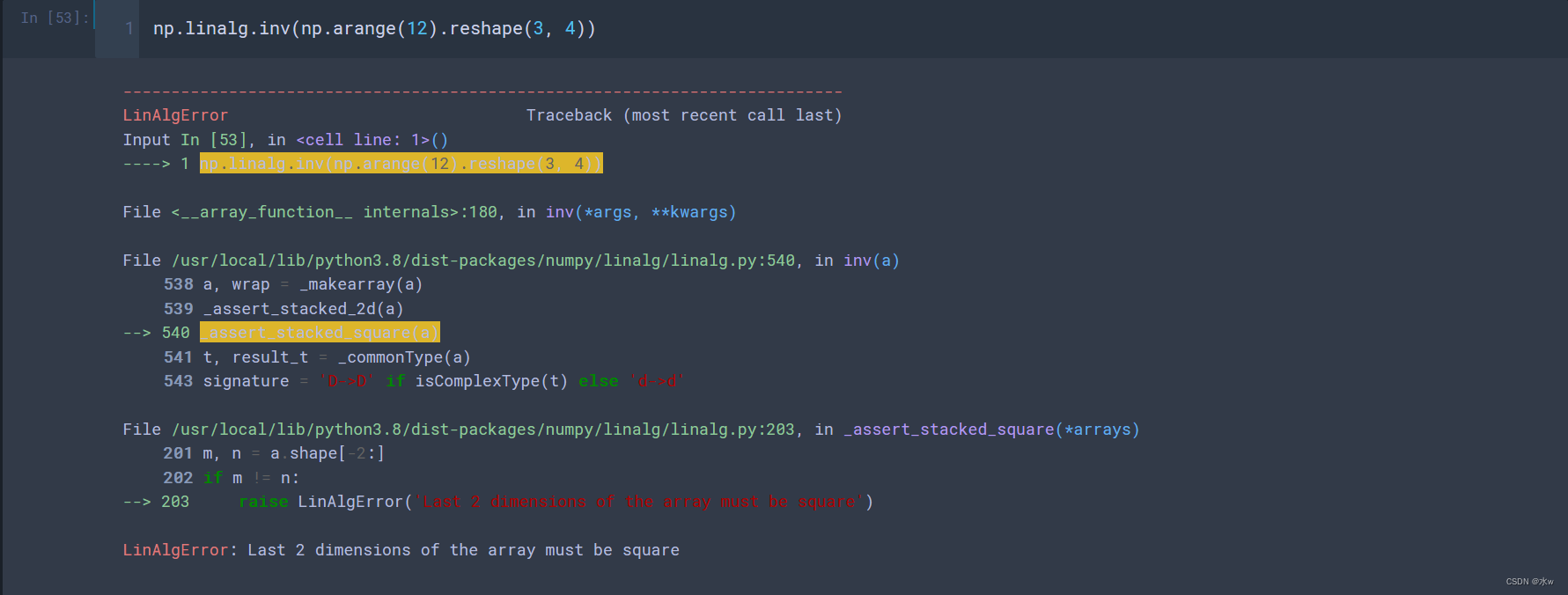
(3)逆矩阵
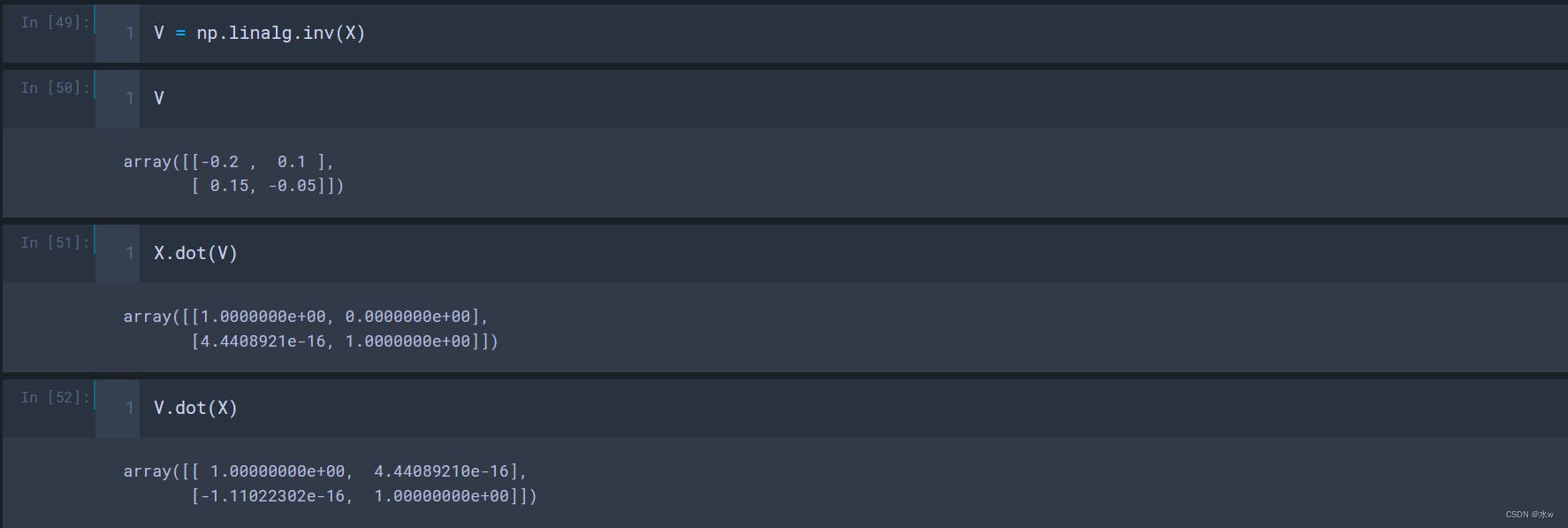
注意:求矩阵的逆时,必须得是方阵,否则会报错,
(4)特征值和特征向量
np.linalg.det(X)
np.linalg.eig(X)
6 Numpy数组的统计运算
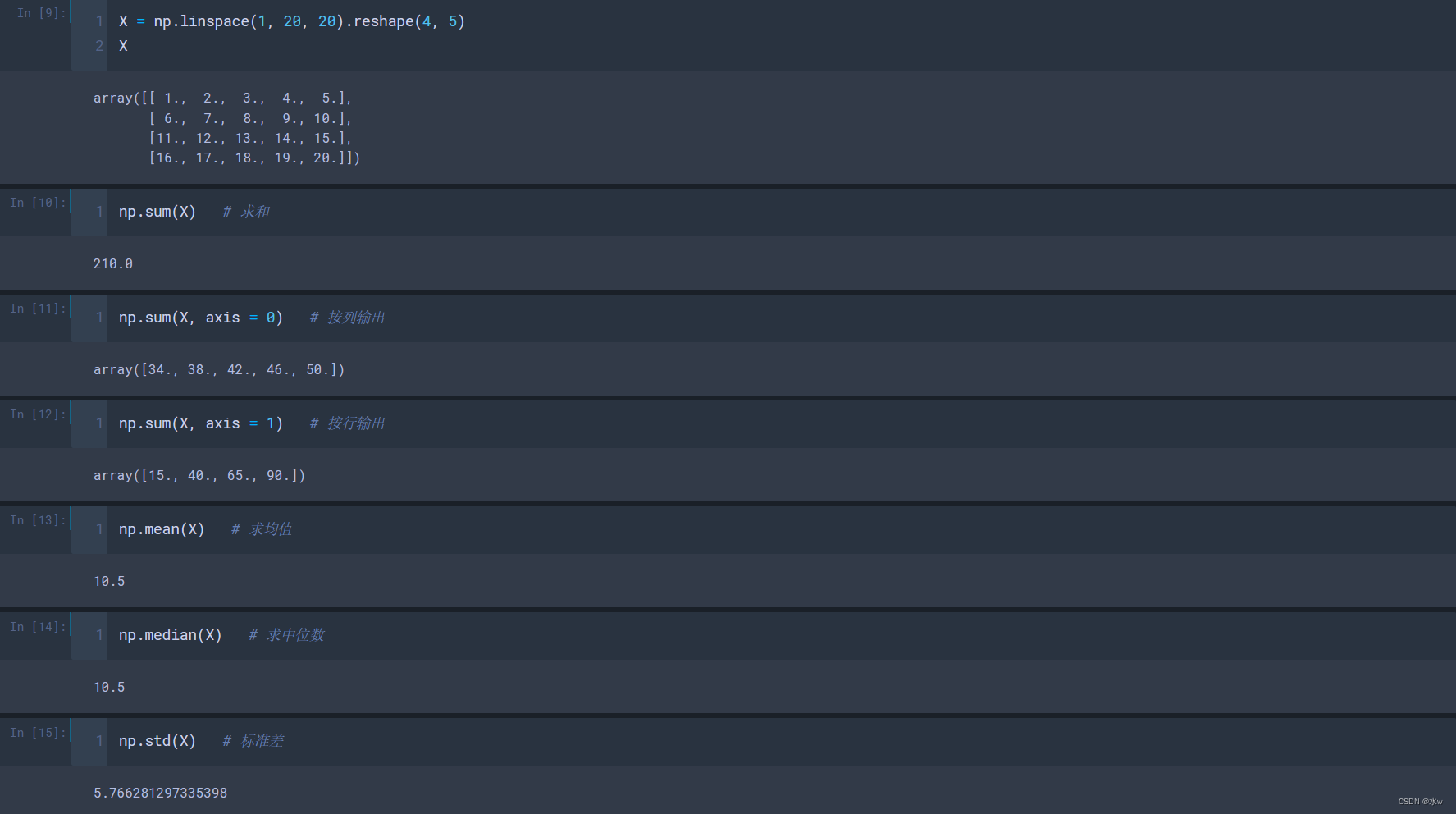
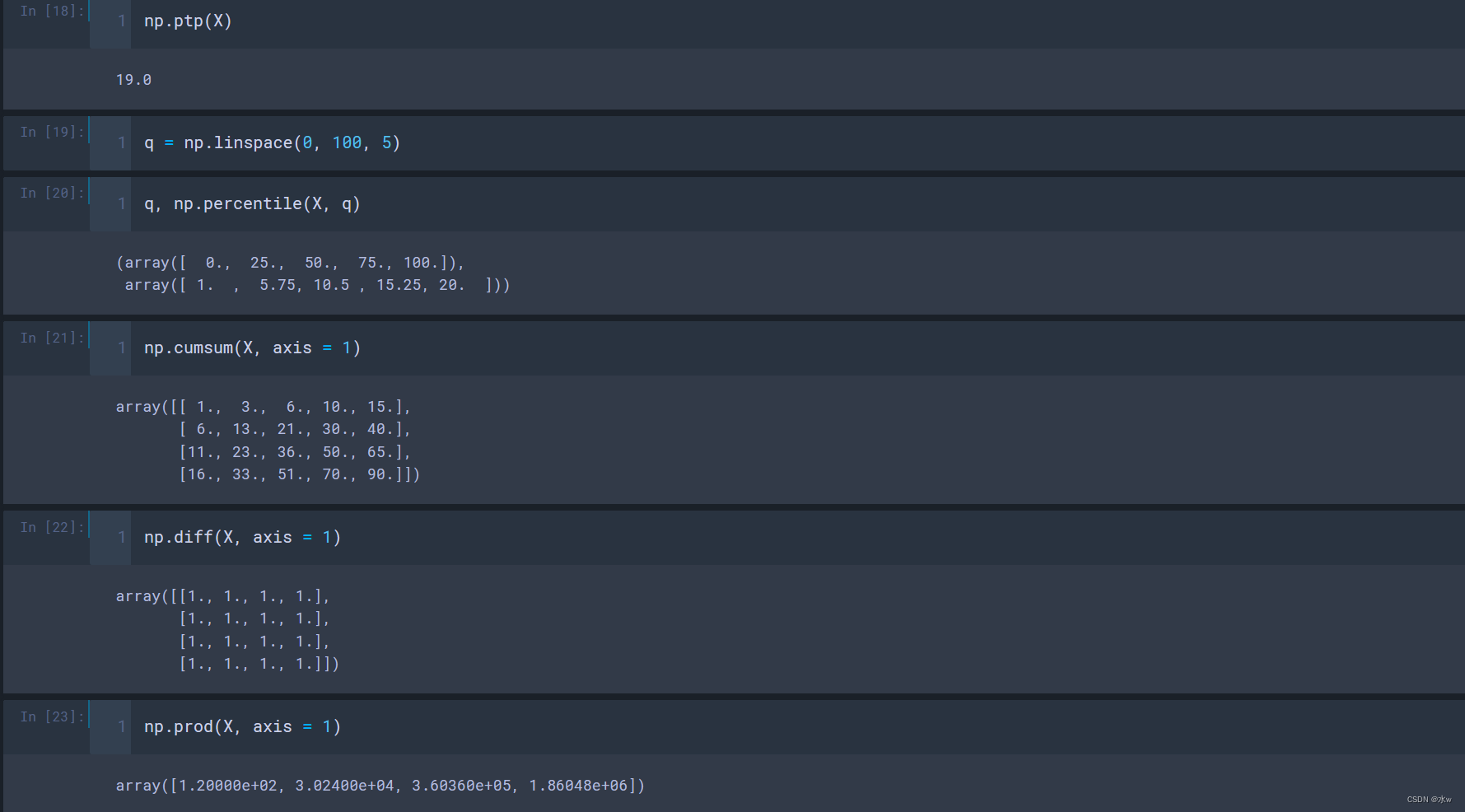
NumPy内置了很多计算方法,其中最重要的统计方法及说明具体如下。
- sum(X, axis=1/0):计算矩阵元素的和;矩阵的计算结果为一个一维数组,需要指定行或者列;
- axis传入0:按列求;
- axis传入1:按行求;
- mean(X, axis=1/0):计算矩阵元素的平均值;矩阵的计算结果为一个一维数组,需要指定行或者列求平均值;
- max(X, axis=1/0):计算矩阵元素的最大值;矩阵的计算结果为一个一维数组,需要指定行或者列求最大值;
- min(X, axis=1/0):计算矩阵元素的最小值;矩阵的计算结果为一个一维数组,需要指定行或者列求最小值;
- mean():计算矩阵元素的平均值;
- median():计算矩阵元素的中位数;
- std()、var():求标准差、方差;
- ptp():描述矩阵中最大元素和最小元素之间的差;
- percentile():可以求任意位置的百分位数;
- cumsum(X, axis=1/0):按行或列统计,求矩阵的累加;
- diff(X, axis=1/0):按行或列统计,计算相邻的差;
- prod(X, axis=1/0):按行或列统计,求矩阵的累积;
需要注意的是,用于这些统计方法的数值类型必须是int或者float。
numpy不只是功能强大,还有一些常用的统计函数:

7 Numpy数组arg运算和排序
Numpy数组arg运算和排序:
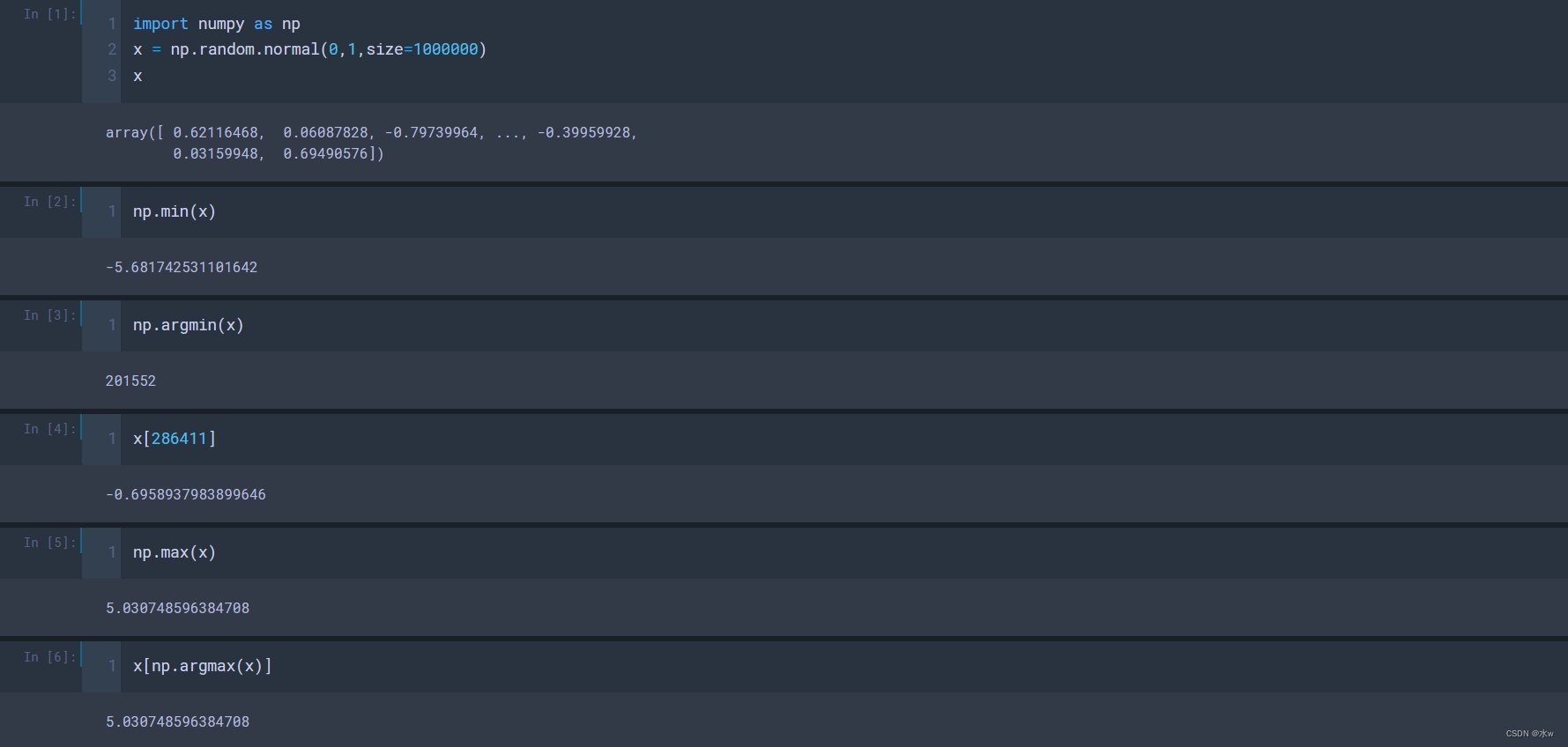
- np. argmin() :最小值索引;
- np.argmax() :最大值索引;
- np. argwhere(x>0.5)指定条件索引,得到值大于0.5的所有索引的位置,可通过x[ind]取出对应的值;
- np.random.shuffle() :打乱顺序;
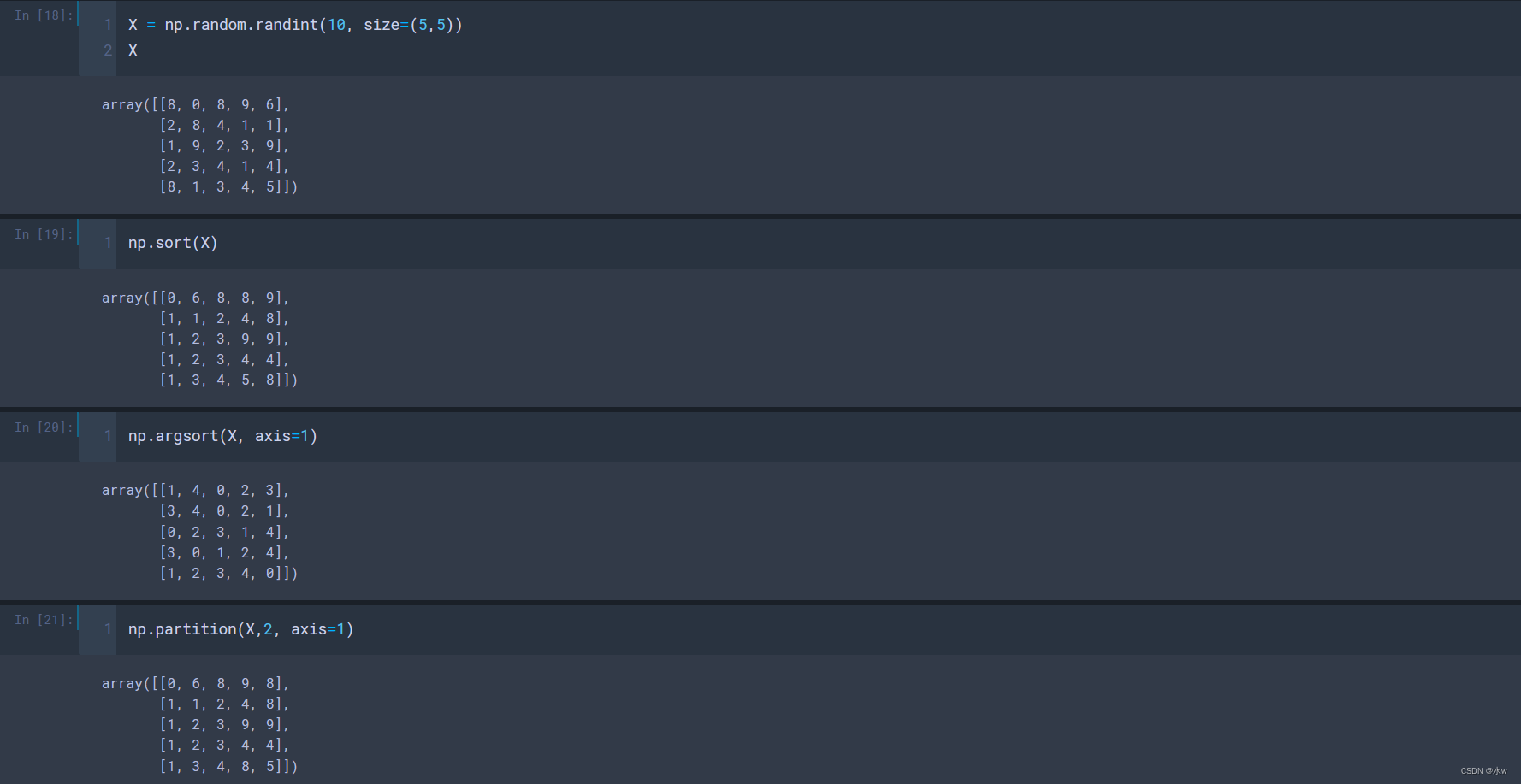
- np.sort() 排序:
默认以最高维数为单元将x重新排序,不改变x本身的值,而是将排序的结果放到了一个新的数组中;
- x.sort() 排序:
改变x本身的值;x[::-1]降序排序;- np. argsort(X, axis=1/0) 排序索引:返回从小到大的索引排序;
- axis传入0:按列;
- axis传入1:按行;
- np. partition(x,5) 指定位置分割:将x分割成小于5和大于5在左右两侧,此处的5是指有序数组情况下的第5个元素;
- np.argpartition(x,5) 分割索引:返回小于5和大于5对应值的索引值;
◼ 最大值 最小值
◼ 排序
(1)
#1.创建一个随机数组x
x = np.arange(10)
x
#结果:array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
#2.将x顺序打乱,且x本身值改变
np.random.shuffle(x)
x
#结果:array([1, 6, 3, 5, 4, 0, 2, 7, 8, 9])
#3.将x重新排序,不改变x本身的值
np.sort(x)
#结果:array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x
#结果:array([1, 6, 3, 5, 4, 0, 2, 7, 8, 9])
#4.直接使用x.sort()排序,改变x本身的值
x.sort()
x
#结果:array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])(2)使用索引,

(3)某些情况下,我们不需要对数组全部排序,我们可以对索引进行切片操作:
np. partition(x,5) 指定位置分割:将x分割成小于5和大于5在左右两侧,此处的5是指有序数组情况下的第5个元素;
np.argpartition(x,5) 分割索引:返回小于5和大于5对应值的索引值;

(3)如果是高维数组,np.sort() 排序是默认以最高维数进行排序的,

8 Numpy数组神奇索引和布尔索引
◼ 神奇索引
import numpy as np
x = np.arange(10) # 取0~9的10个整数组成数组
x
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
x[2:8] # 对数组x切片截取2~8的一个子数组
array([2, 3, 4, 5, 6, 7])
x[2:8:2] # 对数组x切片截取2~8的一个子数组,且步长为2
array([2, 4, 6])
[x[2],x[5],x[8]] # 取第2,5,8三个位置的元素作为数组
[2, 5, 8]
index = [2,5,8] # 更简洁的方法---神奇索引:取第2,5,8三个位置的元素作为数组
x[index]
array([2, 5, 8])
index = np.array([[1,3,5],[2,4,6]]) # 更简洁的方法---神奇索引:取第1,3,5和2,4,6位置的元素作为二维数组
x[index]
array([[1, 3, 5],
[2, 4, 6]])神奇索引用于二维数组的情况:
X = x.reshape(2,-1) # 把x重构成2x5的一个二维数组
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
row = np.array([0,1,0]) # 构建索引,row表示行坐标,clo表示列坐标
col = np.array([0,2,4])
X[row,col] # 把row和col都传给X
array([0, 7, 4]) # 输出了3个数字:0行0列,1行2列,0行4列的三个位置的元素
X[0,col] # 都从第0行取值:取0行0列,0行2列,0行4列的三个位置的元素
array([0, 2, 4])
X[row,:2] # 从前2列取值:取0行前2列,1行前2列,0行前2列的三个位置的元素
array([[0, 1],
[5, 6],
[0, 1]])
col = [True, False, True, False, True] # 还支持传递布尔类型的数组
X[0,col] # 都从第0行取值:取0行0列,0行2列,0行4列的三个位置的元素
array([0, 2, 4]) # 输出这三个True对应的元素◼ 布尔索引
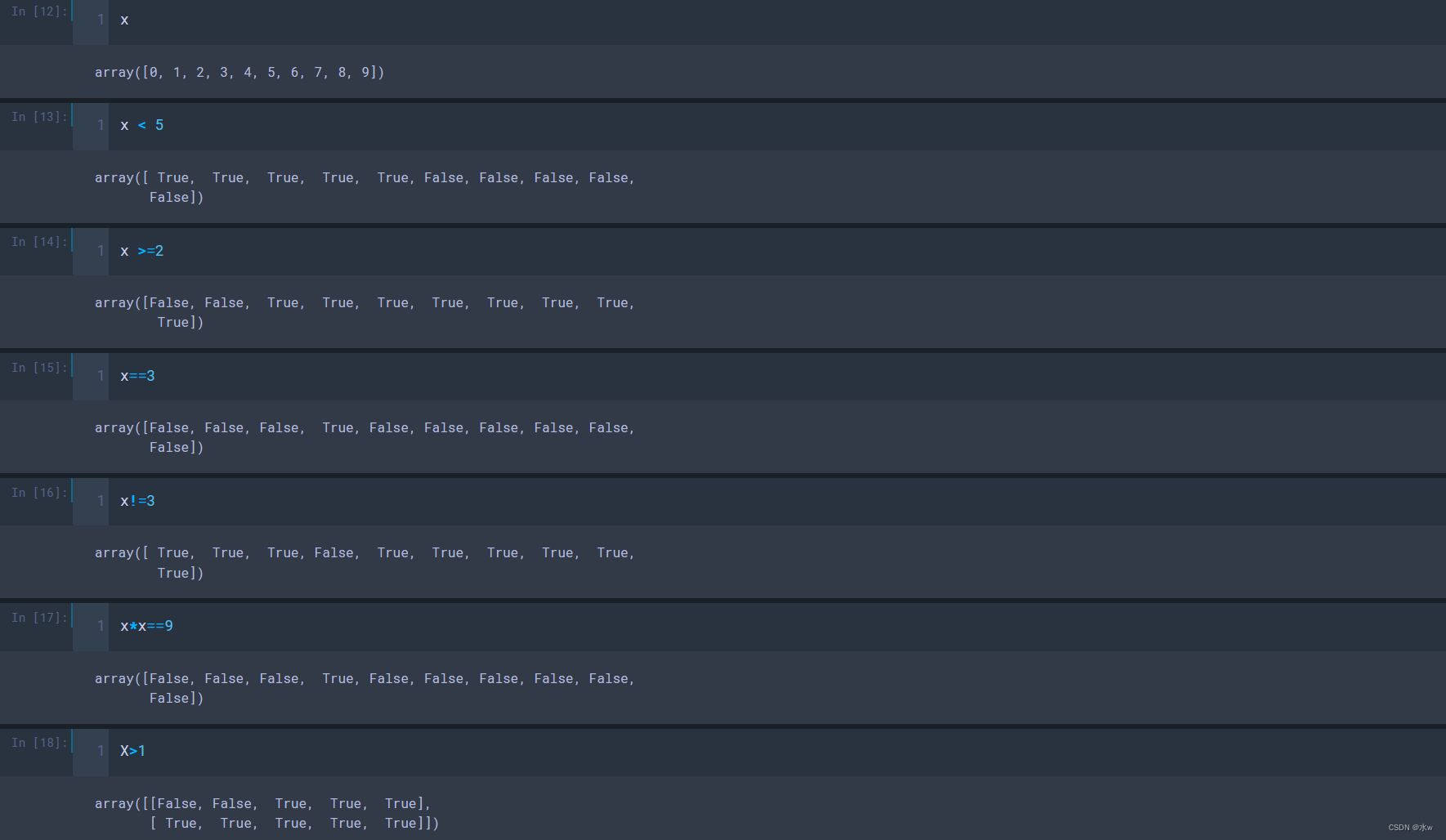
(1)如何得到布尔类型的数组呢?我们可以通过“比较”,
(2)比较结果和神奇索引的同时使用,

我们还可以找到数组X中所有的偶数,

(3)比较的更多应用,
对于一维数组,
- np.count_nonzero(x<5):返回x<5的布尔数组中非0元素的个数;
- np.sum(x<5):返回x<5的布尔数组的求和结果;
- np.any(x<0):求数组中是否有小于0的数;
- np.all(x>0):求数组中的元素是否都是小于0;
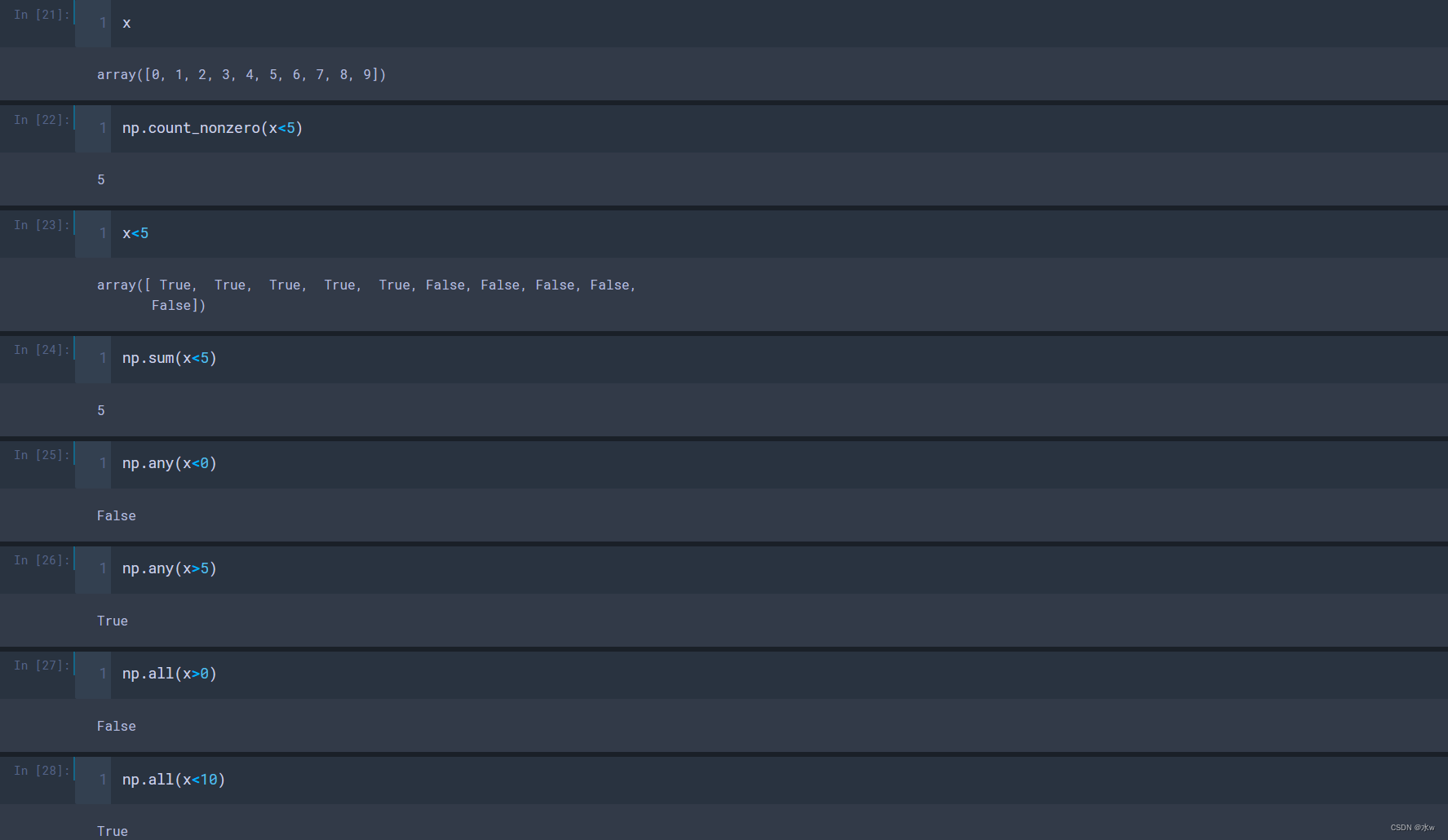
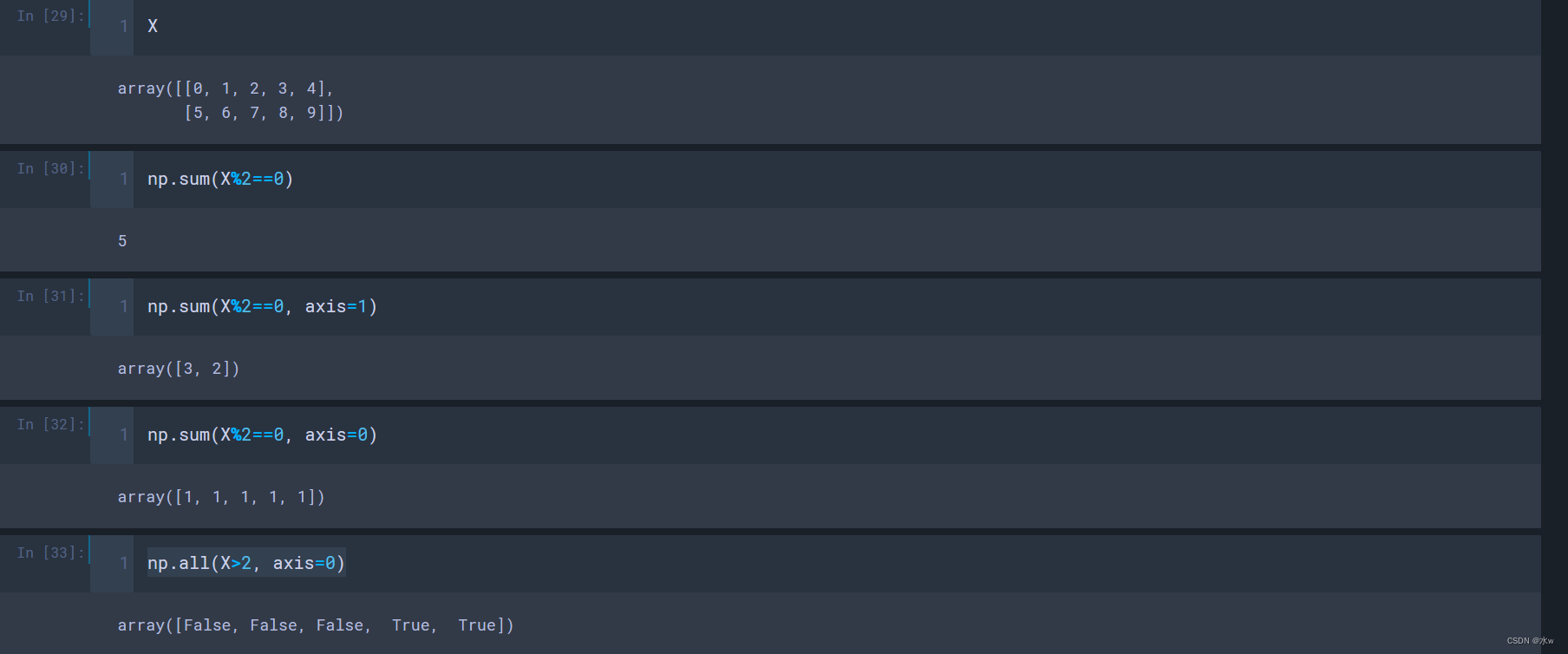
对于二维数组,
- np.sum(X%2==0, axis=1/0):统计每一行/列有多少个元素是偶数;
- np.all(X>2, axis=1/0):统计每一行/列的元素是不是都大于2;
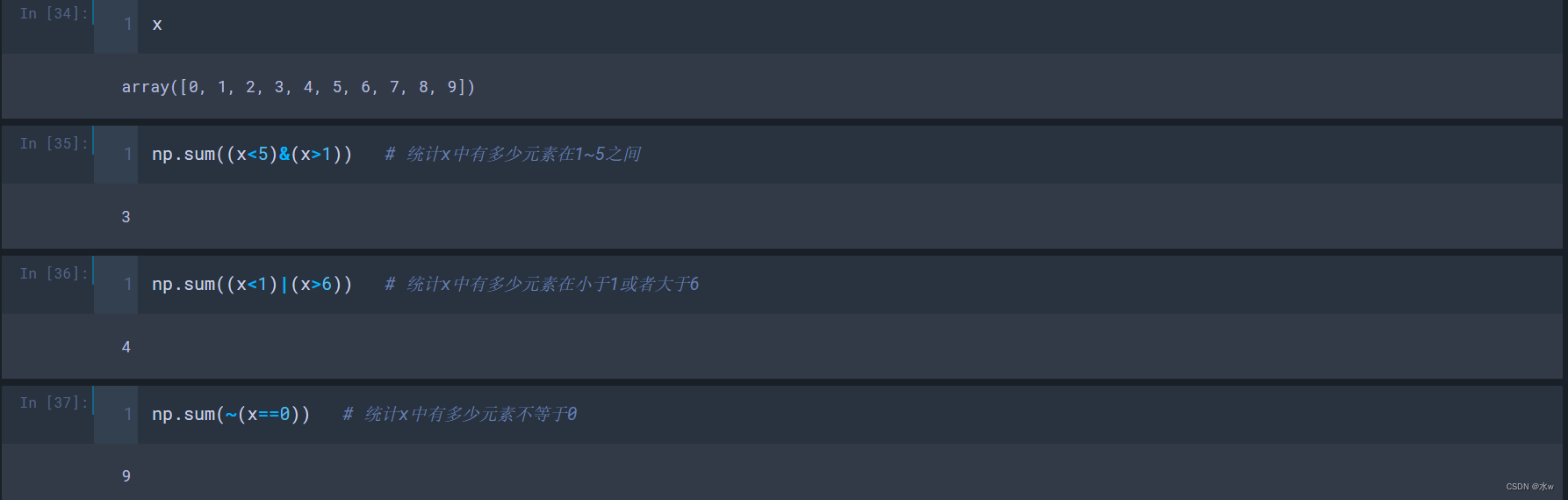
(2)对于多个条件的组合使用:与& 、或| 、非~


![[附源码]计算机毕业设计JAVA科院垃圾分类系统](https://img-blog.csdnimg.cn/7f49d79f67324a979be7256b57cbc4cd.png)











![[附源码]计算机毕业设计JAVA卡牌交易网站](https://img-blog.csdnimg.cn/015abb7c1eb74a50b962f02508f8a9f8.png)
