选择排序
选择排序分为两种一个是堆排序
一个是简单选择排序
简单选择排序

就是从头到尾扫描一遍待排序元素找出最小的
最小的之前的数的往后一位,第一个空间空出来
把最小的元素存入
然后从第二个空间开始变为待排序元素

最后一个元素不用处理
代码实现

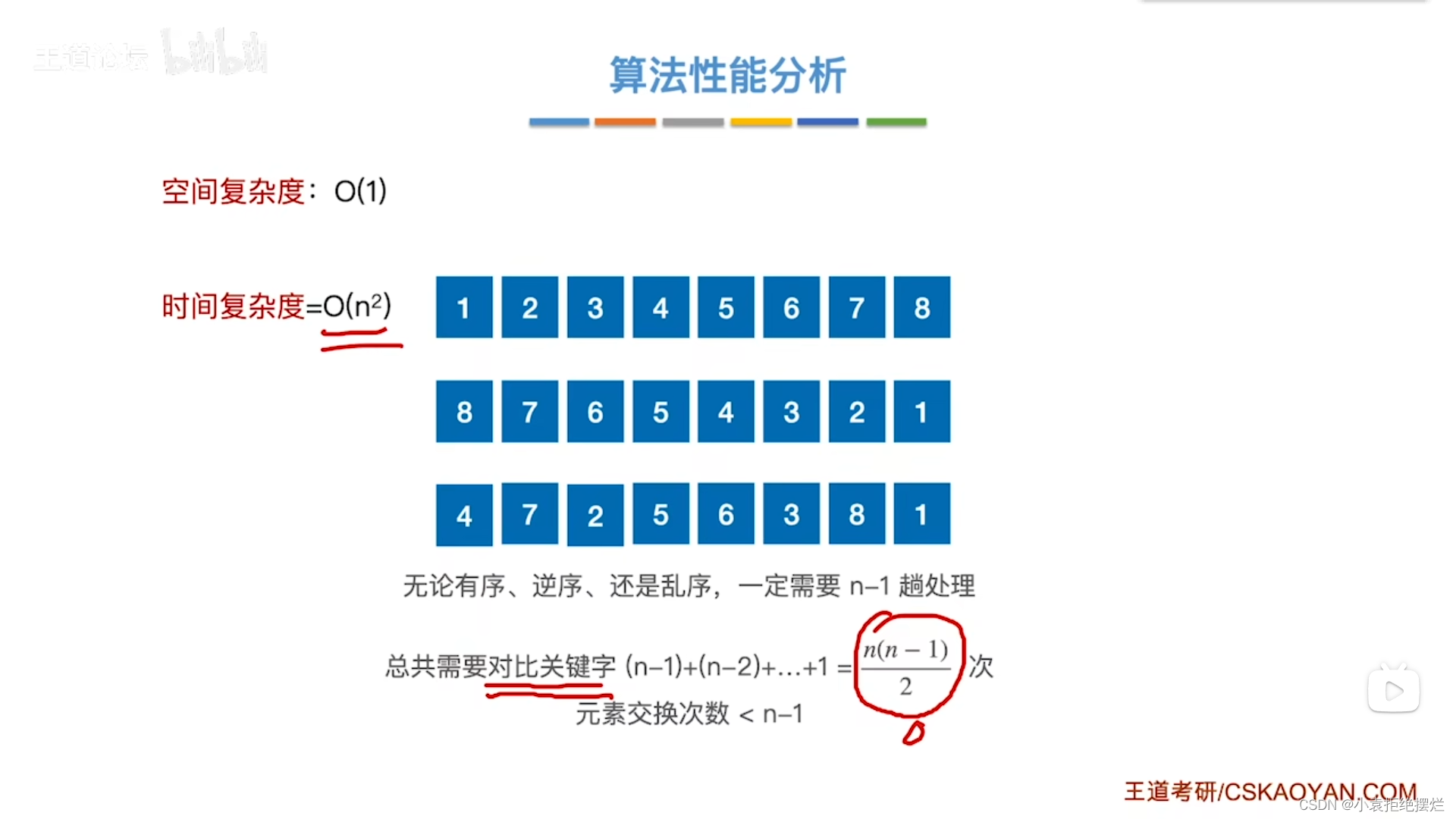
算法性能
小结

堆排序
什么是堆?
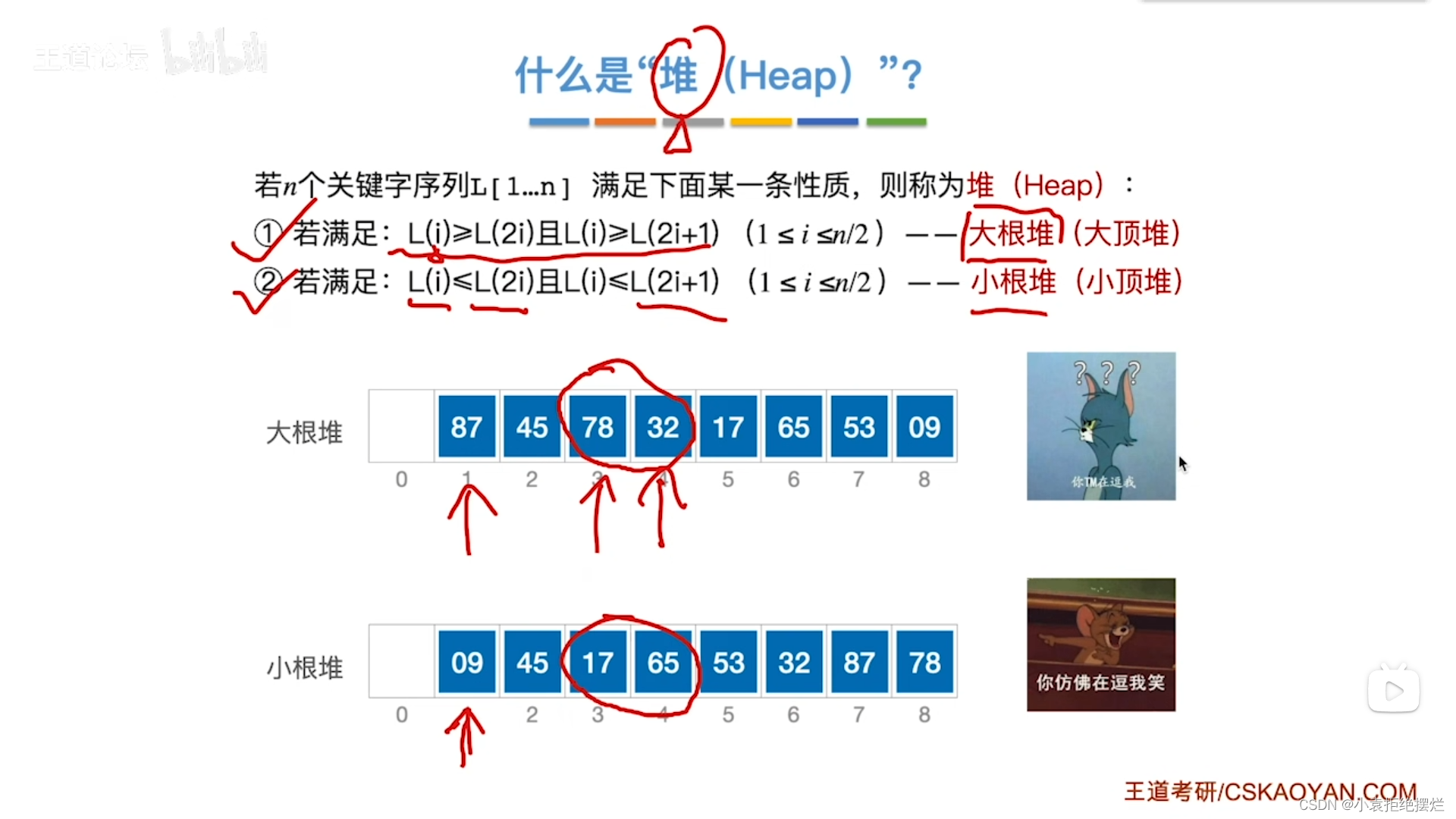
这个不太能直接看得懂哈
为了便于理解我们复习一下

用二叉树解释堆

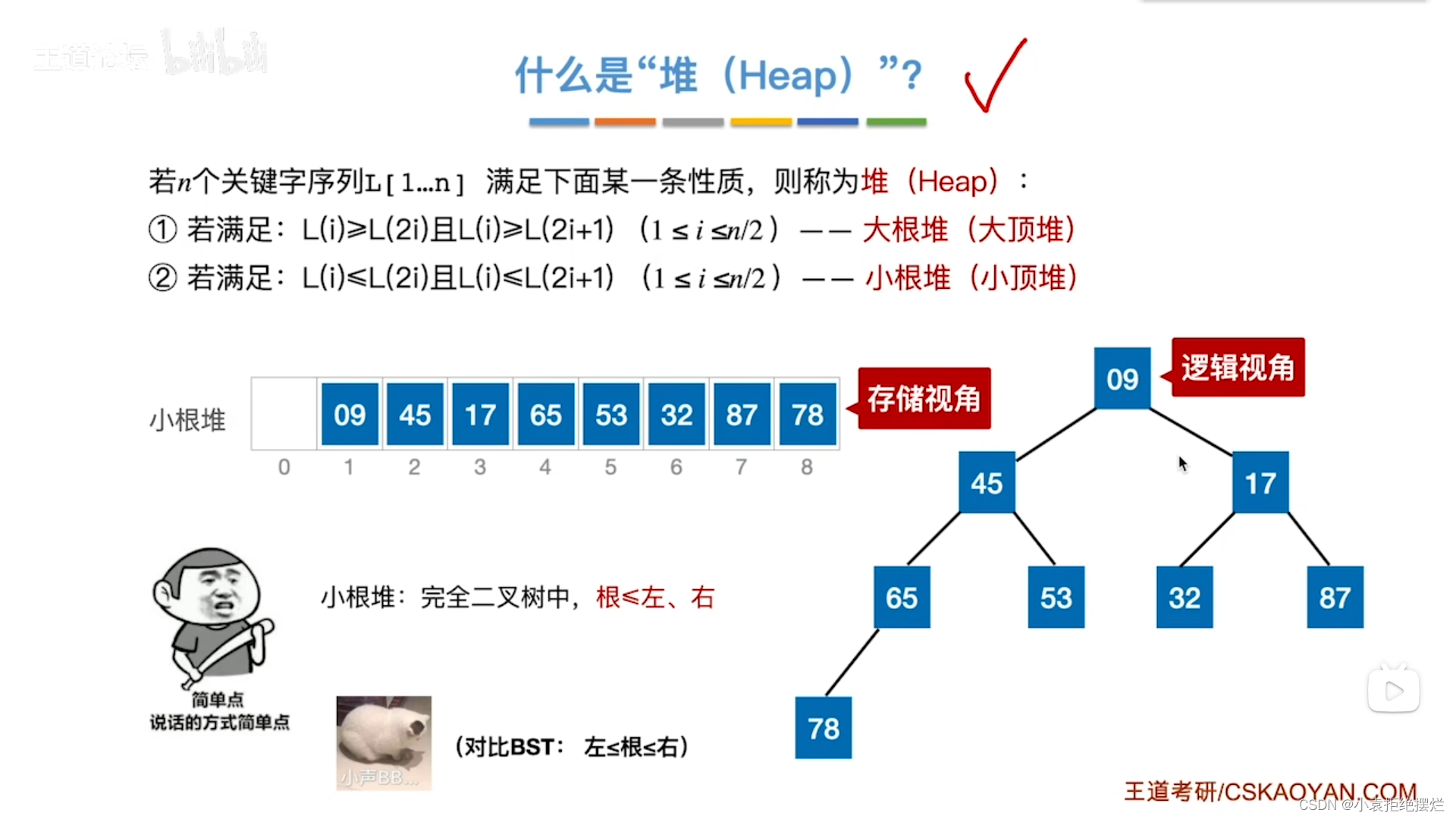
物理结构上看就是连续存储空间的数组
而从逻辑视角上看
其实是一个二叉树
我们可以把L(i)看为根节点L(2i)看为根节点左孩子,L(2i+1)看为根节点的右孩子
这样解释的话
大根堆不就是
每一个根节点大于左右孩子
小根堆解释每一个根节点小于其左右子树
可以自己看一下逻辑存储形式和逻辑形式的关联
怎么进行堆排序?

选择排序(找最大或者最小一个个填入呗),大根堆的最大不就是最头吗data[0]
现在关键是对于一个初始序列如何建立成大根堆找到那个最大值
建立大根堆

处理非终端节点,进行调整
非终端节点从i/2从后往前处理(为什么,因为后面的只有一个孩子,而从头开始的话,不稳定,有很多孩子,我的理解是这样的)
比如这个吧
先从4开始处理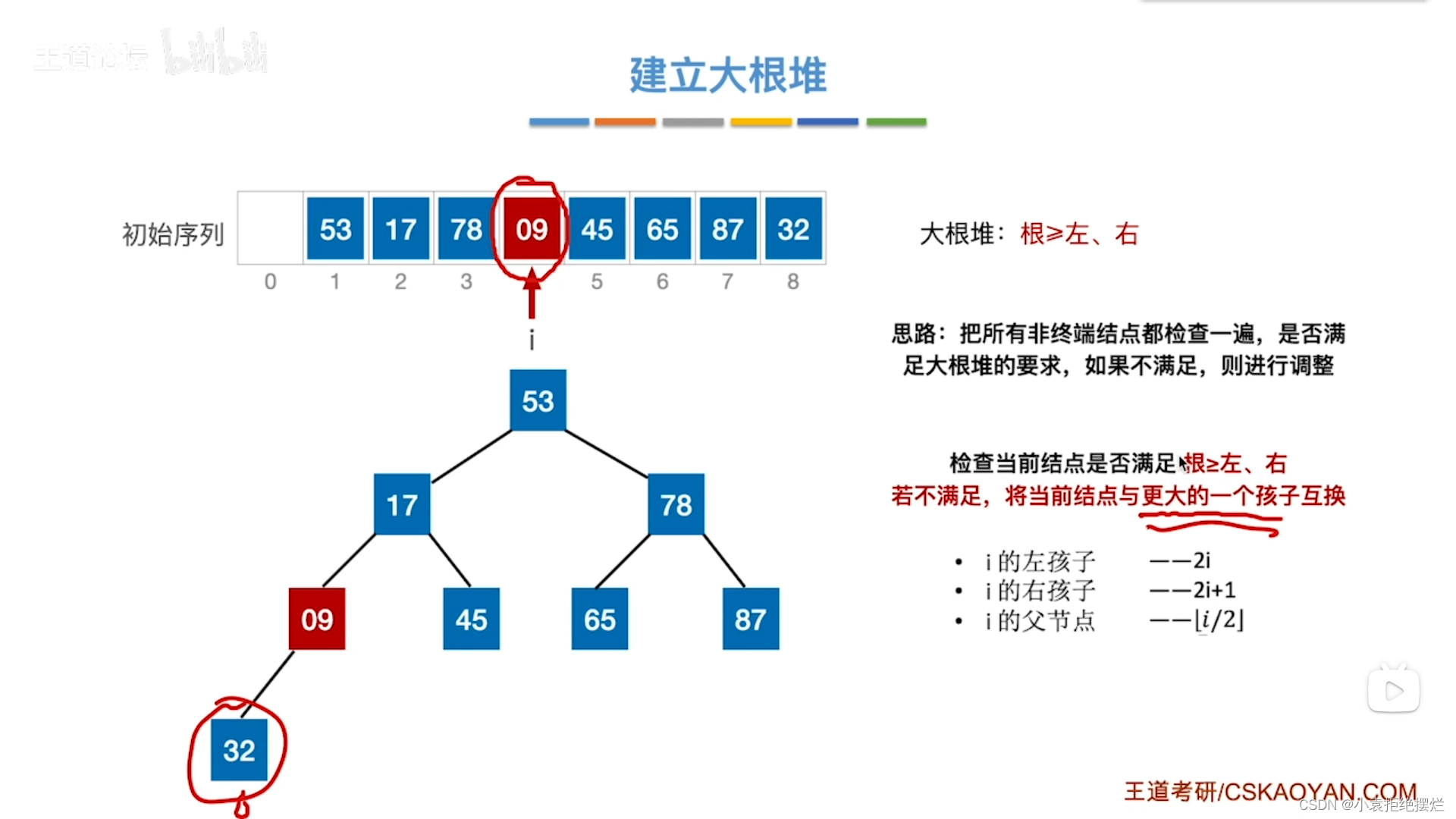
检查孩子,用完全二叉树的顺序存储的特性找对应数组8(2i),不符合,然后找右孩子,右孩子超出数组,没有让根节点和最大的孩子互换
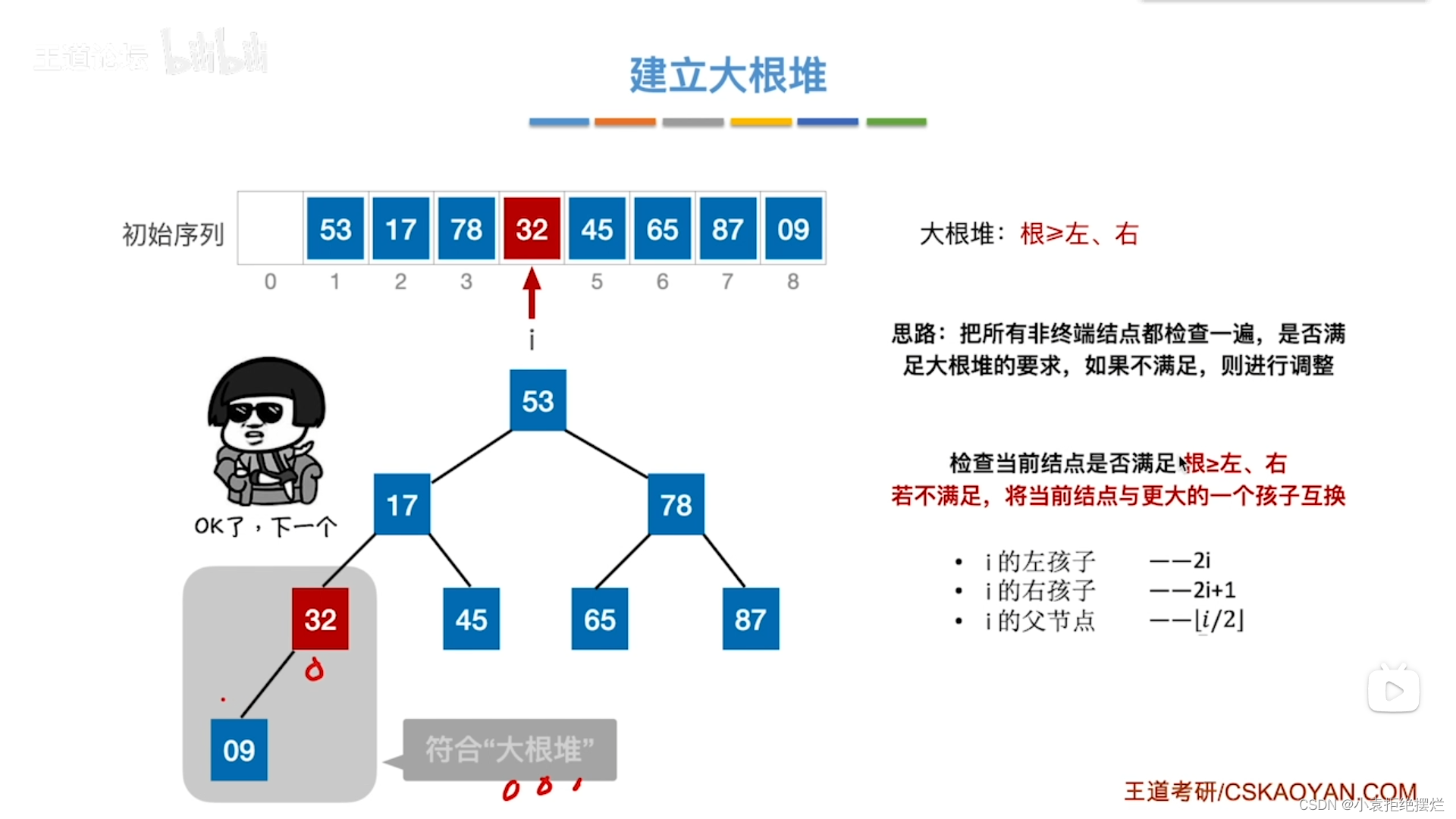
就符合了

然后处理78呗
87>78互换

然后就是2号
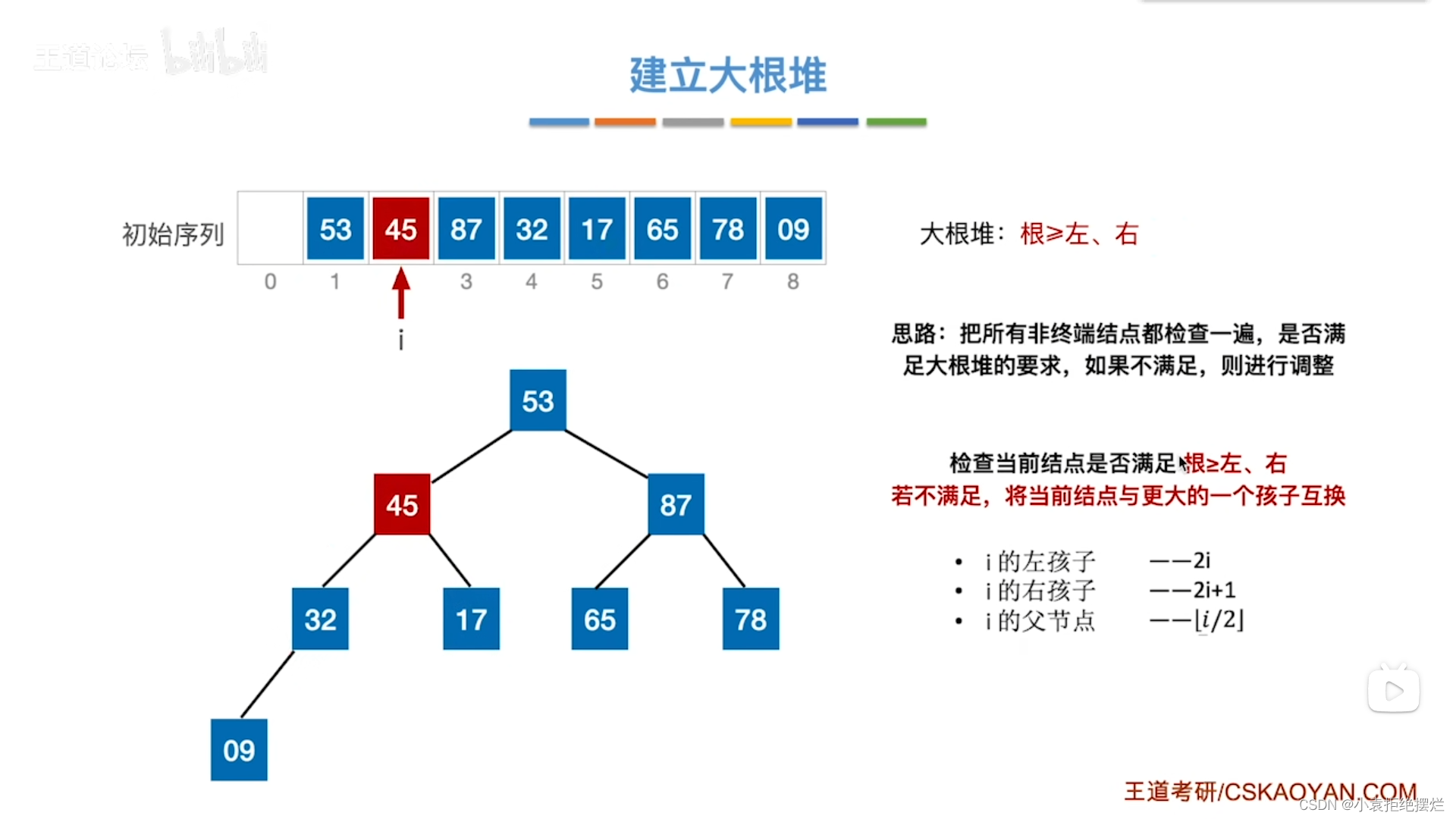
也是互换
最后是根节点

53<87再和87互换
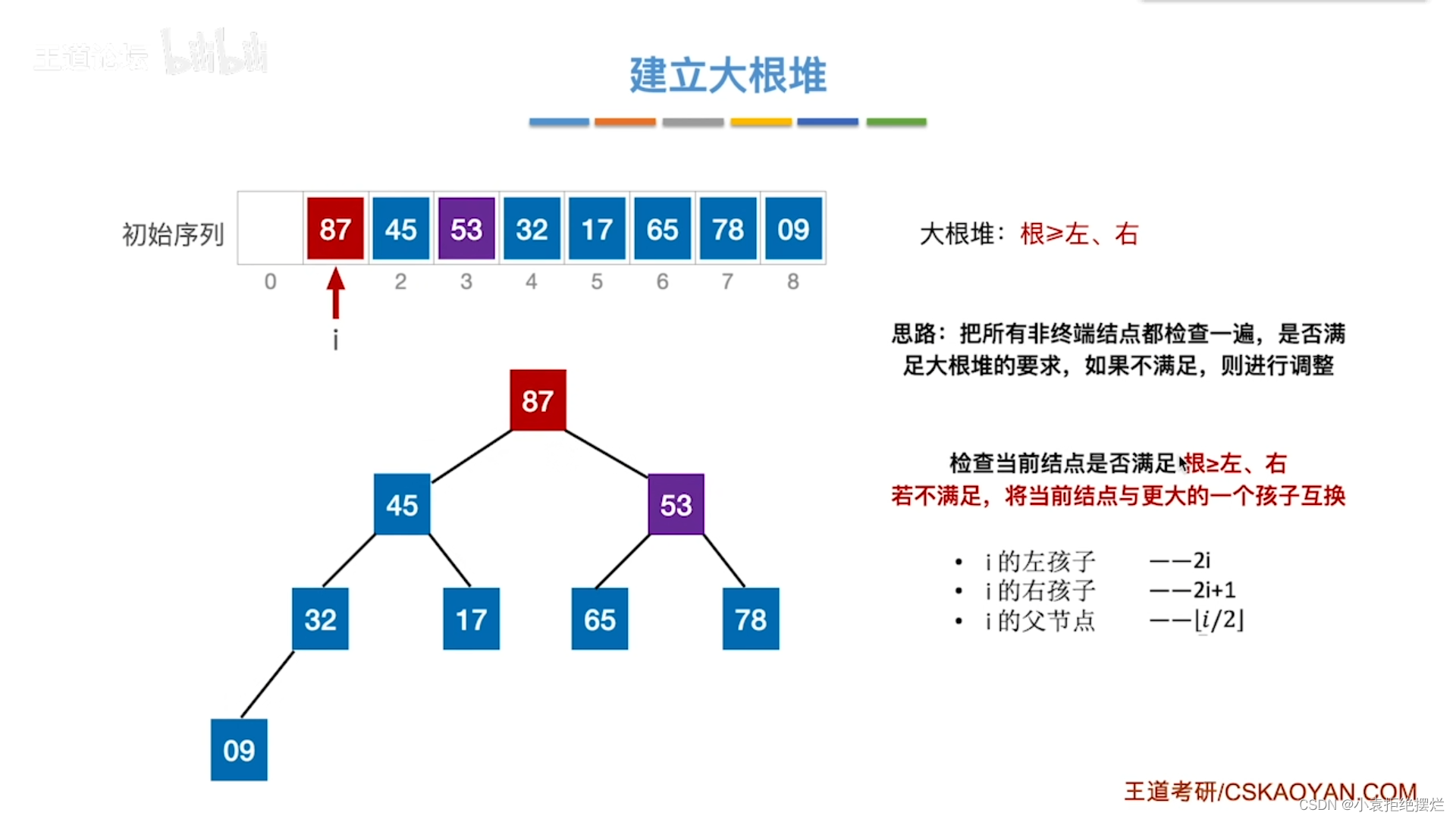
但是这里出现了一个问题 78>53却在53下面不符合大根堆特性
还要再进行一次互换53和78
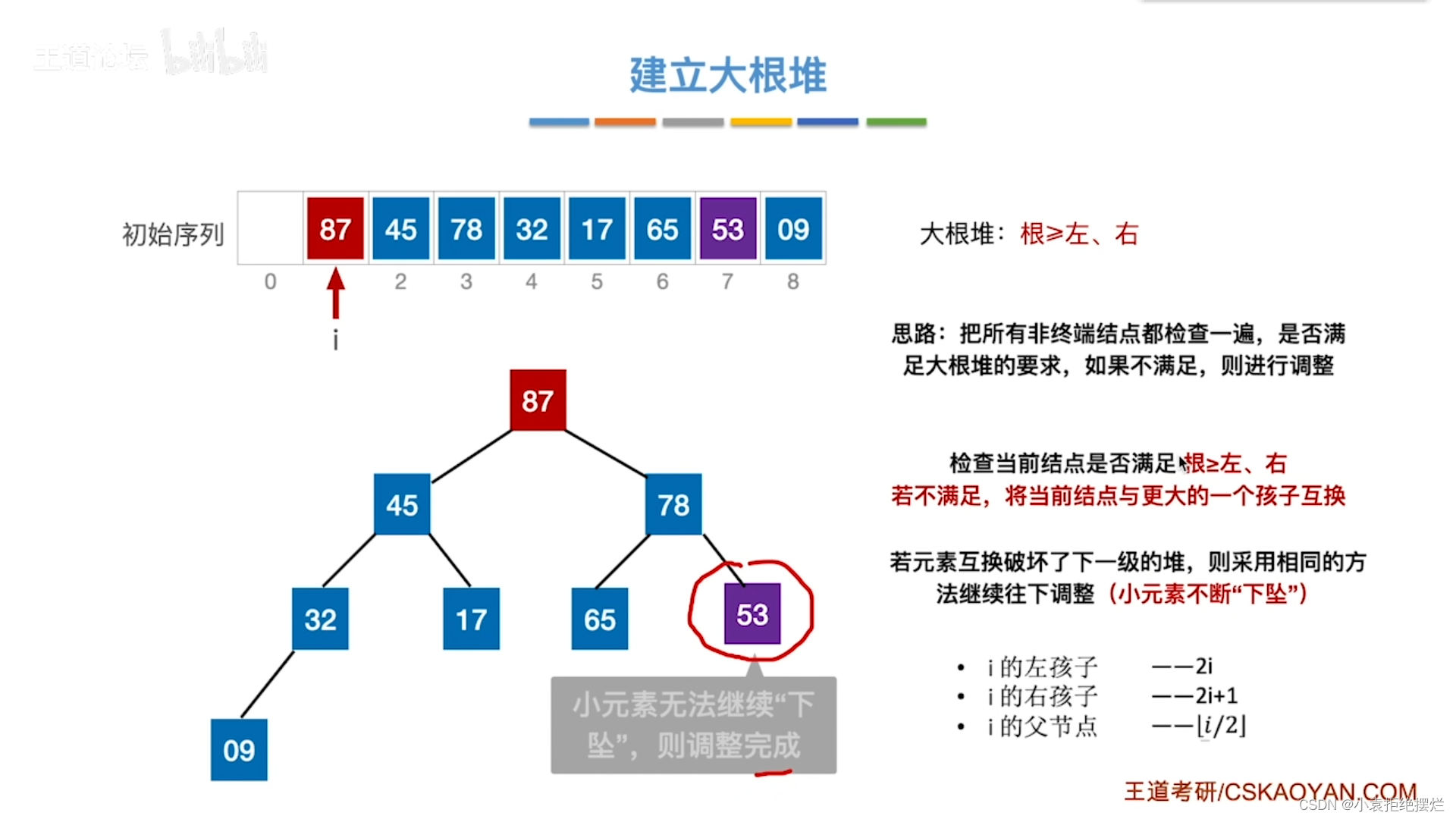
到此结束大根堆的创建了
代码实现

HeadAdjust里面实现了一直向下坠的操作,直至符合大根堆的特性
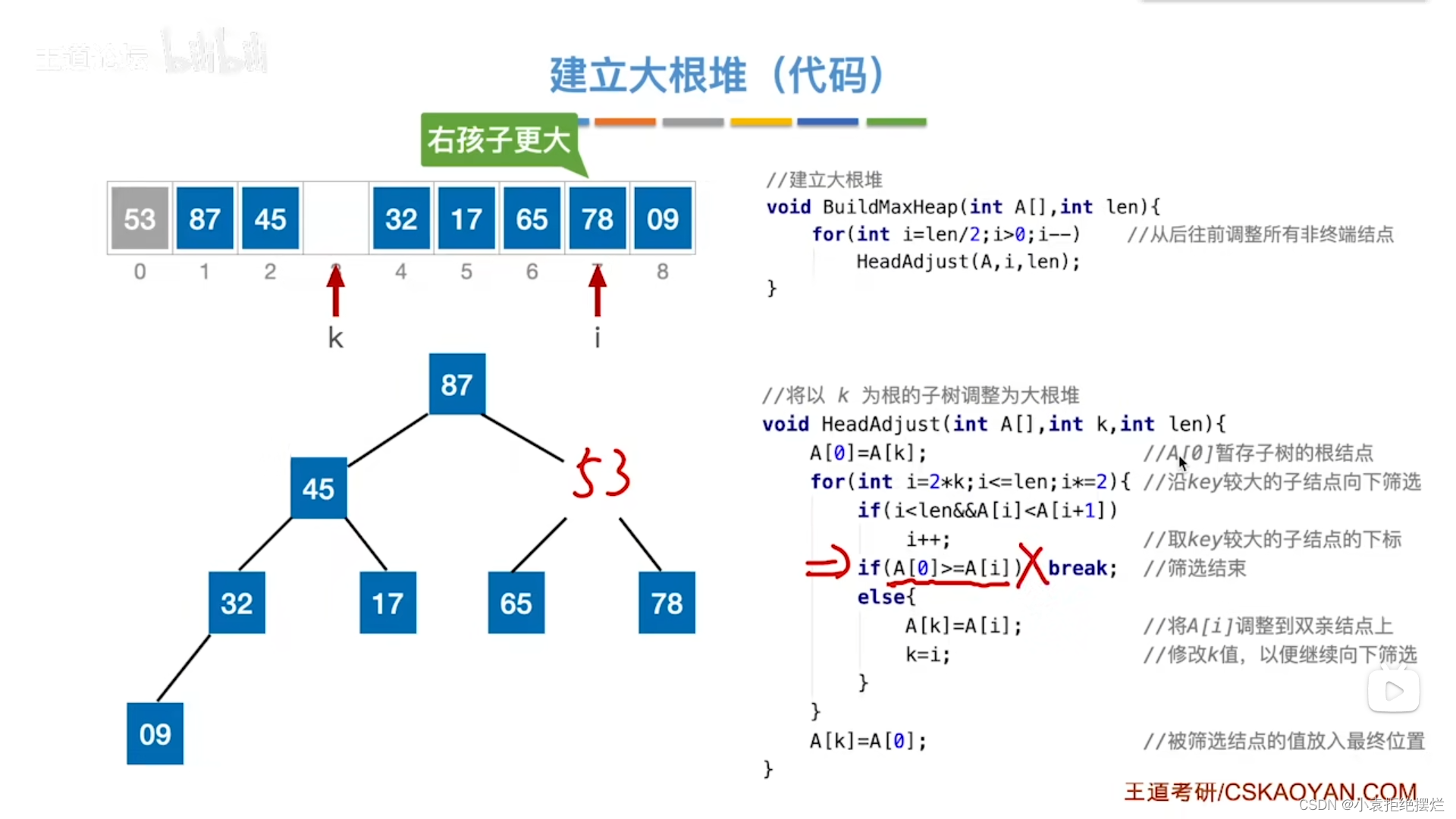
举个例子吧k=1len=8
调整的是A[1]
对应的是53先把53存入A【0】
第二行代码
把i指向A[1]的左孩子
如果说A[1]有右孩子,且右孩子大于左孩子(A[2k+1]>A[2k])
i指向右孩子
如果A[0]>A[i],就是比左右孩子都大,符合大根堆直接退出进行
如果不是的话
else中的
把左孩子右孩子中最大的赋值给A【k】呗(这里是A[1])
然后k变成i,因为交换了值,所以现在要判断再下一个子树是否符合了
再循环,和新k(原k的左孩子或者右孩子)的左孩子右孩子对比,直至符合大根堆
最后就赋值呗
基于大根堆排序

选择堆头元素和堆尾元素互换!因为其他元素不变
所以对于新范围来说(取出最后一个已经排序好的)
值对根节点进行调整即可

每一遍都是这样,先堆头尾互换,再对堆头调整即可

进行n-1遍即可
代码实现

算法效率分析

建堆的时间复杂度O(n)

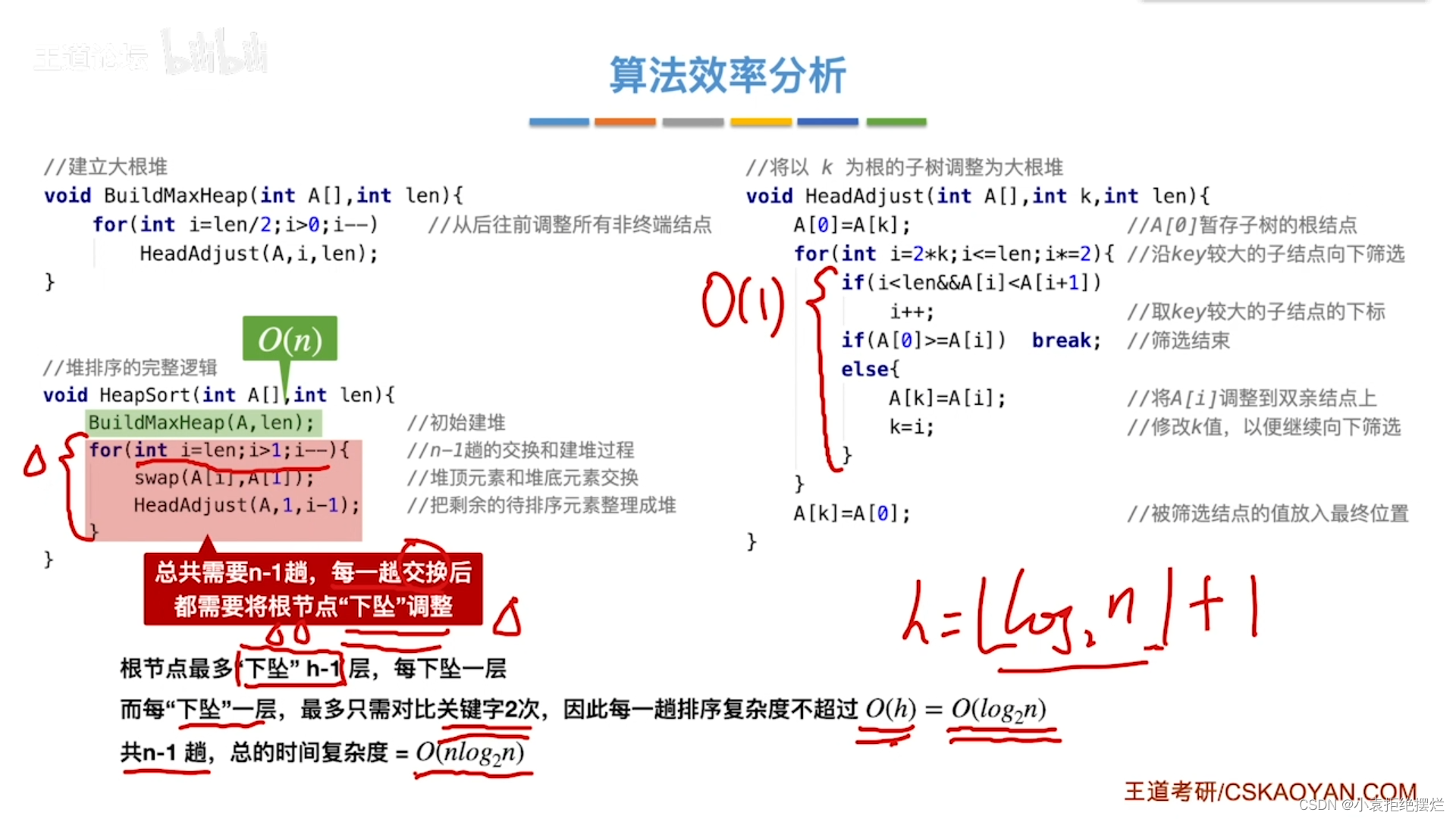
整个堆排序复杂度

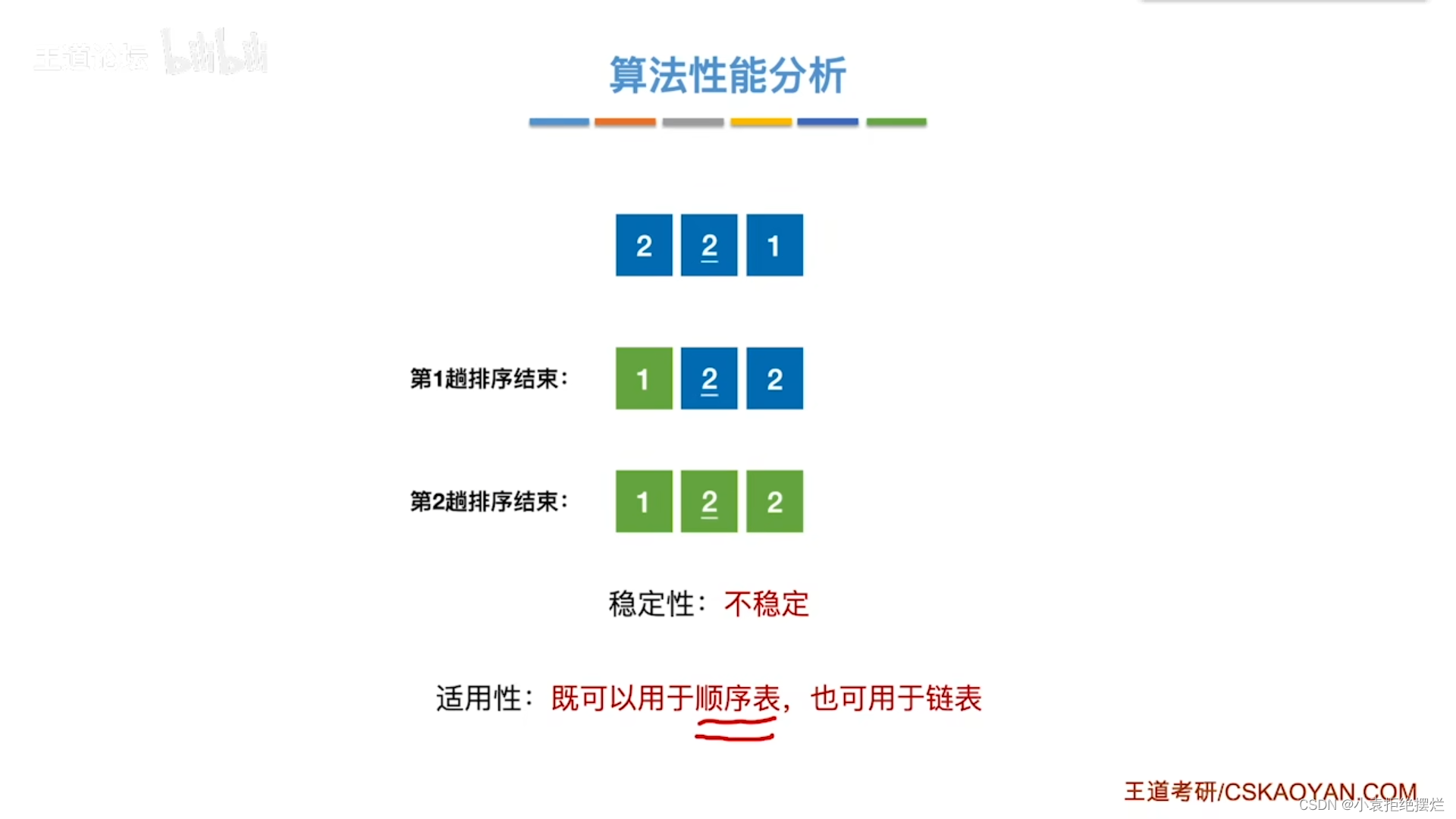
稳定性:不稳定

总结