【参考】
- 官网 curve_fit
- 示例与评估:拟合curve_fit
- 使用矫正的R^2评估非线性模型:拟合评估
- 其他:
- curve_fit()实现任意形式的曲线拟合-csdn
- 拟合优度r^2-csdn
官网示例
拟合函数:
f
(
x
)
=
a
e
−
b
x
+
c
f(x)=ae^{-bx}+c
f(x)=ae−bx+c
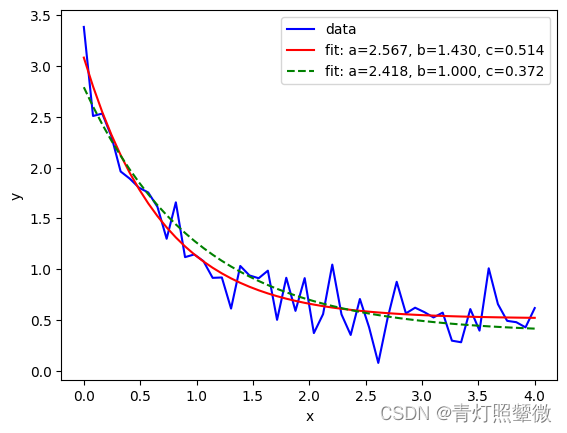
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy as np
def func(x, a, b, c):
return a * np.exp(-b * x) + c
xdata = np.linspace(0, 4, 50)
y = func(xdata, 2.5, 1.3, 0.5)
rng = np.random.default_rng()
y_noise = 0.2 * rng.normal(size=xdata.size)
ydata = y + y_noise
print("--- raw data----")
print(len(xdata), len(ydata))
plt.plot(xdata, ydata, 'b-', label='data')
print("--- curve1----")
popt, pcov = curve_fit(func, xdata, ydata)
print("最优化参数:", popt)
print("协方差:\n", pcov)
plt.plot(xdata, func(xdata, *popt), 'r-',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
print("--- curve2----")
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
print(popt, '\n', pcov)
plt.plot(xdata, func(xdata, *popt), 'g--',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
计算拟合结果的指标
-
总平方和: S S T = ∑ ( y i − y ˉ ) 2 SST=\sum{(y_i-\bar{y})^2} SST=∑(yi−yˉ)2
总平方和(SST) = 回归平方和(SSR)十残差平方和(SSE)
-
回归平方和: S S R = ∑ ( y ^ i − y ˉ ) 2 SSR=\sum{(\hat{y}_i-\bar{y})^2} SSR=∑(y^i−yˉ)2
-
残差平方和: S S E = ∑ ( y i − y ^ i ) 2 SSE=\sum{(y_i-\hat{y}_i)^2} SSE=∑(yi−y^i)2
-
判定系数R-square:
R 2 = S S R S S T = S S T − S S E S S T = 1 − S S E S S T R^2=\frac{SSR}{SST}=\frac{SST-SSE}{SST}=1-\frac{SSE}{SST} R2=SSTSSR=SSTSST−SSE=1−SSTSSE -
矫正判定系数Adjusted R-square: Degree-of-freedom adjusted coefficient of determination
R a d j u s t e d 2 = 1 − ( 1 − R 2 ) ( n − 1 ) n − p − 1 R^2_{adjusted} = 1 - \frac{(1-R^2)(n-1)}{n-p-1} Radjusted2=1−n−p−1(1−R2)(n−1)
其中,n为样本个数,p为特征个数
R-square不适合用于判断非线性拟合的效果
-
M S E MSE MSE (均方差、方差): M S E = S S E / n = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE=SSE/n=\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y}_i)^2} MSE=SSE/n=n1i=1∑n(yi−y^i)2
-
R M S E RMSE RMSE(均方根、标准差):
R M S E = M S E = S S E / n = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 RMSE=\sqrt{MSE}=\sqrt{SSE/n}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y}_i)^2}} RMSE=MSE=SSE/n=n1i=1∑n(yi−y^i)2
未完待续。。。