一、LeetCode1049. 最后一块石头的重量 II
1:题目描述(1049. 最后一块石头的重量 II)
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
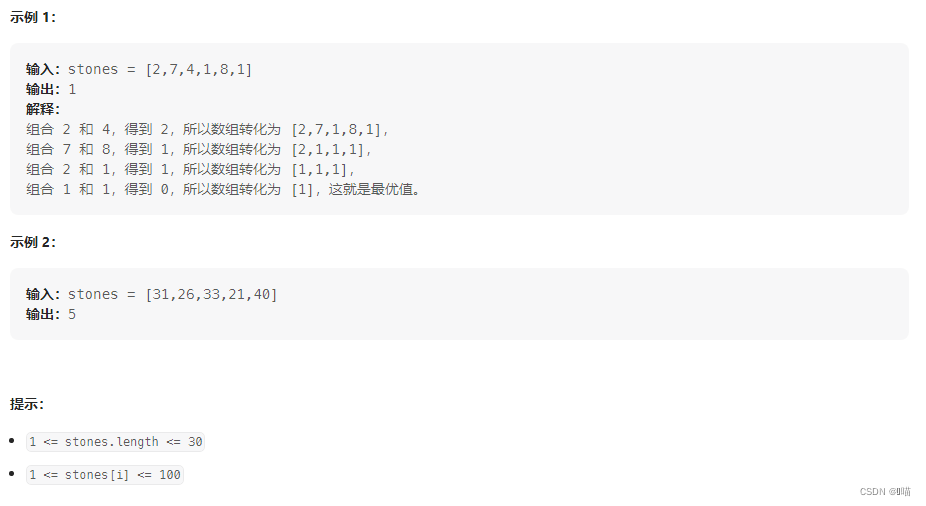
2:解题思路
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
# 将一堆石头分成两堆重量相近的两堆石头,这样两堆石头碰撞之后,得到的重量就是最小重量
# 如何获得两堆重量相近的石头呢?
# 把这一堆石头的重量,除以2,向下取整,就是其中一堆石头的重量
# 另外一堆石头的重量就是原石头总重量-向下取整得到的石头重量
# 然后我们就可以把向下取整得到的石头重量,看做背包容量,石头的重量看做物品的重量和价值
# 就将这个问题转化成了0-1背包问题,就可以用01背包的思路来进行求解
#
target = sum(stones) // 2 # 求石头总重量的一半,向下取整
# 定义dp数组,dp[j]表示,容量为j的背包得到的最大价值为dp[j]
# 初始化,j=0时,无法装物品,所以dp[0]=0
# 其他的是求上一个容量所装的最大价值和上一个容量所装的最大价值+当前物品重量的最大值,所以其他元素也初始化为0
dp = [0] * (target+1) # 防止元素溢出,长度为target+1
# 遍历顺序,先遍历物品,再倒序遍历背包容量(防止同一个物品重复加入)
for i in range(len(stones)):
# j从target开始,从后向前遍历,直到j>=sones[i]
for j in range(target, stones[i]-1, -1):
# 递推公式,0-1背包的递推公式为:dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
# 本题中石头的重量就是石头的价值,所以dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
# dp[target]是容量为target的背包所能装的最大价值,及石头的最大重量
# sum(stones)-dp[target]是,剩余的石头重量
res = sum(stones)-dp[target] - dp[target] # res就是两堆石头碰撞之后,所剩的最小重量
return res二、LeetCode494. 目标和
1:题目描述(494. 目标和)
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

2:解题思路
确定dp数据的含义:
dp[j]表示,装满容量为j的背包有dp[j]种方式
递推公式:
不考虑nums[i]的情况下,填满容量为j的背包,有dp[j]种方法。
那么考虑nums[i]的话(只要搞到nums[i]),凑成dp[j]就有dp[j - nums[i]] 种方法。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 dp[5]。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 dp[5]。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 dp[5]
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 dp[5]
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 dp[5]
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
所以递推公式为:dp[j] += dp[j - nums[i]](求组合类问题的公式,都类似于这种)
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
# 将nums分为两个数组,一个数组放正数(left),一个数组放负数(right)
# 由题意得出:
# sun(left) + sum(right) = sum(nums)
# sum(left) - sum(right) = target
# 可得出:sun(left) - (sum(nums)-sum(left)) = target,sum(left) = (target+sum(nums))/2
# 即正数数组left中,有多少种方式,可以使得sum(left) = (target+sum(nums))/2
# 由此可看做0-1背包问题
# 定义:dp[j]表示,装满容量为j的背包有dp[j]种方式
# 初始化:j=0时,dp[0] = 1
# 递推公式:dp[j] += dp[j-nums[i]]
# 遍历顺序,先遍历物品,再倒序遍历背包容量,直到背包容量小于物品重量
if abs(target) > sum(nums) or (target+sum(nums))%2 != 0:
# 如果正数数组的和不能被2整除的话,说明找不到符合题意的组合
# 若目标值的绝对值已经大于了nums的元素和,说明没有符合题意的组合
return 0
left = int((target+sum(nums))/2) # 正数数组的和
dp = [0] * (left+1)
dp[0] = 1
for i in range(len(nums)):
for j in range(left, nums[i]-1, -1):
dp[j] += dp[j-nums[i]]
return dp[left]三、LeetCode474. 一和零
1:题目描述(474. 一和零)
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
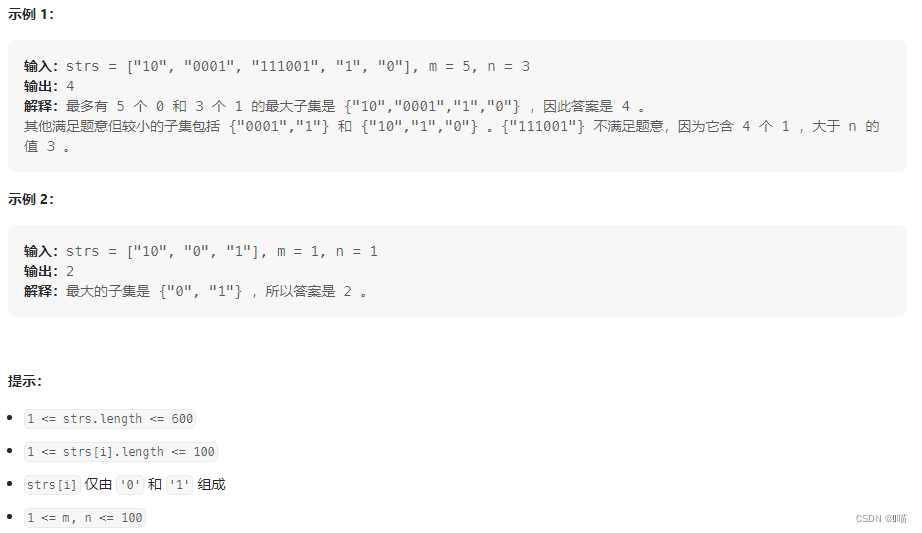
2:解题思路
确定dp数组含义:
定义dp[i][j],表示装满i个0,j个1,最多有dp]i[j]个物品;即最多有i个0和j个1的strs的最大子集的大小为dp[i][j]
递推公式:
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有x个0,y个1。
dp[i][j] 就可以是 dp[i - x][j - y] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
字符串的x和y相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。 只不过物品的重量有了两个维度而已。
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
# 看做0-1背包问题,背包容量是m个0,n个1
# 定义dp[i][j],表示装满i个0,j个1,最多有dp]i[j]个物品;即最多有i个0和j个1的strs的最大子集的大小为dp[i][j]
# 递推公式:dp[i][j] = max(dp[i][j], dp[i-x][j-y]+1),x表示当前物品有x个0,y个1
# 初始化:当i=0,j=0,初始化为0,即dp[0][0] = 0,其他元素也初始化为0
# 遍历顺序,先遍历字符串(物品),即strs,统计物品中有x个0,y个1
# 再倒序遍历m,n
dp = [[0] * (n + 1) for _ in range(m + 1)]
for s in strs: # 遍历字符串
x, y = 0, 0
for item in s:
# 统计字符串中,0和1的个数
if item == "0": x += 1
else: y += 1
for i in range(m, x-1, -1): # 倒序遍历0的个数,1的个数
for j in range(n, y-1, -1):
dp[i][j] = max(dp[i][j], dp[i-x][j-y]+1)
return dp[m][n]