一道质量挺高的题(个人感觉),题目说了每次要删除一条边,分成两棵树,那么很容易想到用并查集去维护。但是问题在于如果要将原来那棵树分成新的两个树必然不能使用路径压缩,如图所示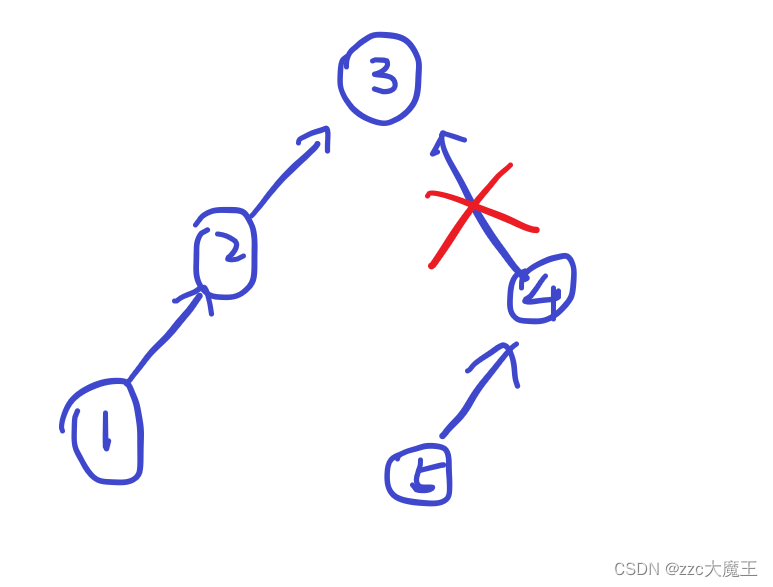
如果使用了路径压缩那就会失去父子关系,就分不出两棵树了。按照这个思路每次分一次树就要沿着这个节点去找一下他的父节点曾经是否有过4,有的话就分到树A,没有的话就分到树B,这样才能分出新的两棵树。
每个节点都爬一次那不累死了吗
我们的难点在于分割出两棵树,但是对于并查集来说,分割是难事,但合并可不是难事。
正难则反!
正着来不行,那我们就把所有操作都逆过来,那最难的分割不就变成合并了吗!

逆向操作,我们执行查询的时候,查询之前的所有删边和修改都要已经被执行。
往上走,就相当于还原每一步的历史值,所以要保留所有节点的原值。
首先是经典的并查集。
并查集怎么使用取决于自己的定义,比如
定义f[i]=j为,i节点在树j中
定义f[i]=j为,i节点在集合j中不会并查集的移步【模板】并查集 - 洛谷
这道题输入貌似也挺多的,不会快读的可以看一下我的洛谷 P3905 道路重建#Spfa+快读_zzc大魔王的博客-CSDN博客 前半部分快读内容
逆向操作的话,那么删掉所有边的情况才是初始状态,也就是所有不需要被删的边,都加上。
为了保证操作的正确性先原模原样的把输入都输入了(逃
struct {
int opt,e,u,val,a;//a为原值
}o[MAXNM];
int find(int x){//并查集路径压缩
if(f[x]==x)return x;
else return f[x]= find(f[x]);
}//找到节点x所在的树
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch xor 48),ch=getchar();
return x;
}//一个平平无奇的快读
inline void READ(){
n=read(),m=read();
for(int i=1;i<=n;++i){
a[i]=read();
}
for(int i=1;i<=n-1;++i){
edge[i].first=read();
edge[i].second=read();
}
for(int i=1;i<=m;++i){
o[i].opt=read();
if(o[i].opt==1){
o[i].e=read();
del[o[i].e]=true;//记录一下被删掉的边
}else if(o[i].opt==2){
o[i].u=read();
o[i].val=read();
}else if(o[i].opt==3){
o[i].u=read();
}
}
}//单纯的输入,没有任何操作
//为了方便逆序操作,建立一个结构体把输入都存下来
inline void build(){//逆序操作的初始状态
for(int i=1;i<=n;++i)//初始化并查集
f[i]=i;
for(int i=1;i<=n-1;++i){//不需要删的边建回去
if(!del[i]){
int f1= find(edge[i].first),f2= find(edge[i].second);
f[f1]=f2;
}
}
}
完成了上述必要的初始化操作之后我们就可以正式开始逆序操作了。
TLE代码(50分)
#include <bits/stdc++.h>
using namespace std;
const int MAXNM=1e5+1;
struct {
int opt,e,u,val,a;//a为原值
}o[MAXNM];
int n,m,a[MAXNM],f[MAXNM];
stack<int>ans;
pair<int,int>edge[MAXNM];
bitset<MAXNM>del;
int find(int x){
if(f[x]==x)return x;
else return f[x]= find(f[x]);
}//找到节点x所在的树
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch xor 48),ch=getchar();
return x;
}
inline void READ(){
n=read(),m=read();
for(int i=1;i<=n;++i){
a[i]=read();
}
for(int i=1;i<=n-1;++i){
edge[i].first=read();
edge[i].second=read();
}
for(int i=1;i<=m;++i){
o[i].opt=read();
if(o[i].opt==1){
o[i].e=read();
del[o[i].e]=true;//删边
}else if(o[i].opt==2){
o[i].u=read();
o[i].val=read();
}else if(o[i].opt==3){
o[i].u=read();
}
}
}//单纯的输入,没有任何操作
inline void build(){
//初始化并查集
for(int i=1;i<=n;++i)
f[i]=i;
for(int i=1;i<=n-1;++i){
if(!del[i]){
int f1= find(edge[i].first),f2= find(edge[i].second);
f[f1]=f2;
}
}
}//不需要删的建回去
// n个节点,n-1条边,m个操作
int main(){
READ();
build();
for(int i=1;i<=m;++i){//记录要修改的原值,并修改
if(o[i].opt==2){
int u=o[i].u;
o[i].a=a[u];
a[u]=o[i].val;
}
}
for(int i=m;i>=1;i--){//逆向操作
int opt=o[i].opt;
if(opt==1){//分割变合并
int e=o[i].e;
int u=edge[e].first,v=edge[e].second;
f[find(u)]=find(v);
}else if(opt==2){//返回历史原值
int u=o[i].u;
a[u]=o[i].a;
}else if(opt==3){//求出u树的权值
int u=o[i].u;
int tot=0;
for(int j=1;j<=n;++j){
if(find(j)== find(u))tot+=a[j];
}
ans.push(tot);
}
}
//由于执行的是逆序操作,答案逆序输出才是正序
while(!ans.empty()){
printf("%d\n",ans.top());
ans.pop();
}
return 0;
}显然,让我们超时的是操作3,一个n的复杂度才找到树的权值,理论上我们在合并这棵树的时候就可以做一次加法来求出树的权值,以及修改权值的时候稍作调整,所以再建立一个数组来求和即可。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int MAXNM=1e5+1;
struct {
int opt,e,u,val,a;//a为原值
}o[MAXNM];
int n,m,a[MAXNM],f[MAXNM],sum[MAXNM];
//定义f[i]=j为节点i在树j中.sum[i]=j为树i的权值为j
stack<int>ans;
pair<int,int>edge[MAXNM];
bitset<MAXNM>del;
int find(int x){
if(f[x]==x)return x;
else return f[x]= find(f[x]);
}//找到节点x所在的树
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch xor 48),ch=getchar();
return x;
}
inline void READ(){
n=read(),m=read();
for(int i=1;i<=n;++i){
a[i]=read();
}
for(int i=1;i<=n-1;++i){
edge[i].first=read();
edge[i].second=read();
}
for(int i=1;i<=m;++i){
o[i].opt=read();
if(o[i].opt==1){
o[i].e=read();
del[o[i].e]=true;//删边
}else if(o[i].opt==2){
o[i].u=read();
o[i].val=read();
}else if(o[i].opt==3){
o[i].u=read();
}
}
}//单纯的输入,没有任何操作
inline void build(){
//初始化并查集
for(int i=1;i<=n;++i)
f[i]=i;
//初始化每棵树的权值
for(int i=1;i<=n;++i)
sum[i]=a[i];
for(int i=1;i<=n-1;++i){
if(!del[i]){
int f1= find(edge[i].first),f2= find(edge[i].second);
f[f1]=f2;
//f1并到f2
sum[f2]+=sum[f1];
sum[f1]=0;
}
}
}//不需要删的建回去
// n个节点,n-1条边,m个操作
int main(){
READ();
build();
for(int i=1;i<=m;++i){//记录要修改的原值,并修改
if(o[i].opt==2){
int u=o[i].u;
int fu= find(u);
//a[u]变成了o[i].val,差值o[i].val-a[u]
sum[fu]+=o[i].val-a[u];
o[i].a=a[u];
a[u]=o[i].val;
}
}
for(int i=m;i>=1;i--){//逆向操作
int opt=o[i].opt;
if(opt==1){//分割变合并
int e=o[i].e;
int u=edge[e].first,v=edge[e].second;
int fu= find(u),fv= find(v);
f[fu]=fv;
//fu并到fv
sum[fv]+=sum[fu];
sum[fu]=0;
}else if(opt==2){//返回历史原值
int u=o[i].u;
int fu= find(u);
//a[u]的值变为了o[i].a,差值为o[i].a-a[u]
sum[fu]+=o[i].a-a[u];
a[u]=o[i].a;
}else if(opt==3){//求出u树的权值
int u=o[i].u;
int fu= find(u);
ans.push(sum[fu]);
}
}
//由于执行的是逆序操作,答案逆序输出才是正序
while(!ans.empty()){
printf("%d\n",ans.top());
ans.pop();
}
return 0;
}树并了之后,为了保持思维的连贯性,最好将先前的树清空。但是对于并查集来说,从零散数据合并成一个集合,先前被合并的集合必然不会再被使用,所以可以不清空。
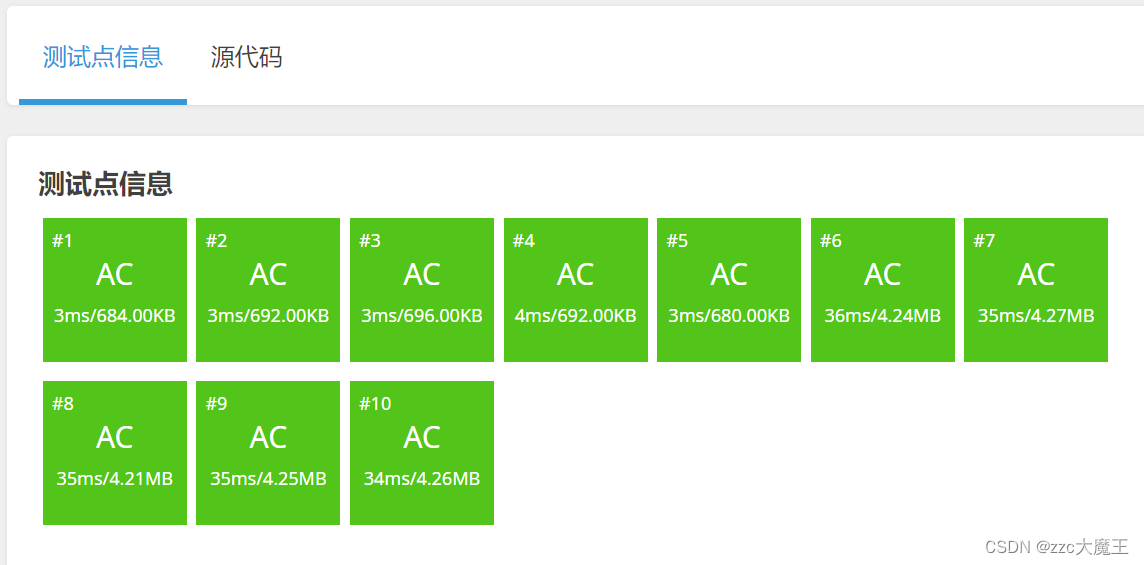
上述操作都是精细活,因为本身考点只是逆向思维和并查集,每一步都要仔细去写,包括数据类型也要好好的判断,不然容易WA。
这道题n*val最大情况为1e8,仅1亿,而int的大小是大于21亿的,所以不需要long long。



![[附源码]Python计算机毕业设计宠物短期寄养平台](https://img-blog.csdnimg.cn/1b4e2ddcc7834f3090ac44b86c75d074.png)