👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

灰狼优化（GWO）算法是基于灰狼社会等级及其狩猎与合作策略的新兴算法。该算法于2014年推出，已被大量研究人员和设计师使用，因此原始论文的引用次数超过了许多其他算法。在Niu等人最近的一项研究中，介绍了这种算法优化现实世界问题的主要缺点之一。总之，他们表明，随着问题的最佳解决方案从0发散，GWO的性能会下降。

在贪婪非分层灰狼优化器（G-NHGWO）中，通过对原始GWO算法进行直接修改，即忽略其社会等级，我们能够在很大程度上消除这一缺陷，并为该算法的未来使用开辟了新的视角。通过将所提方法应用于基准和实际工程问题，验证了该方法的效率。

文献来源：

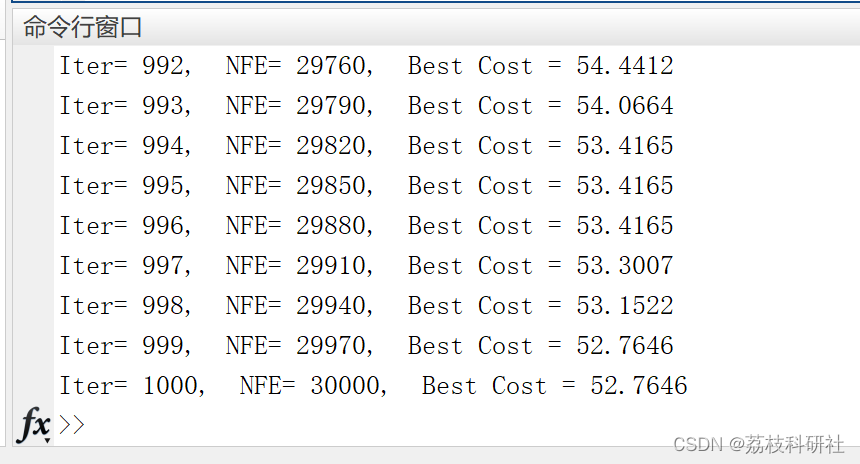
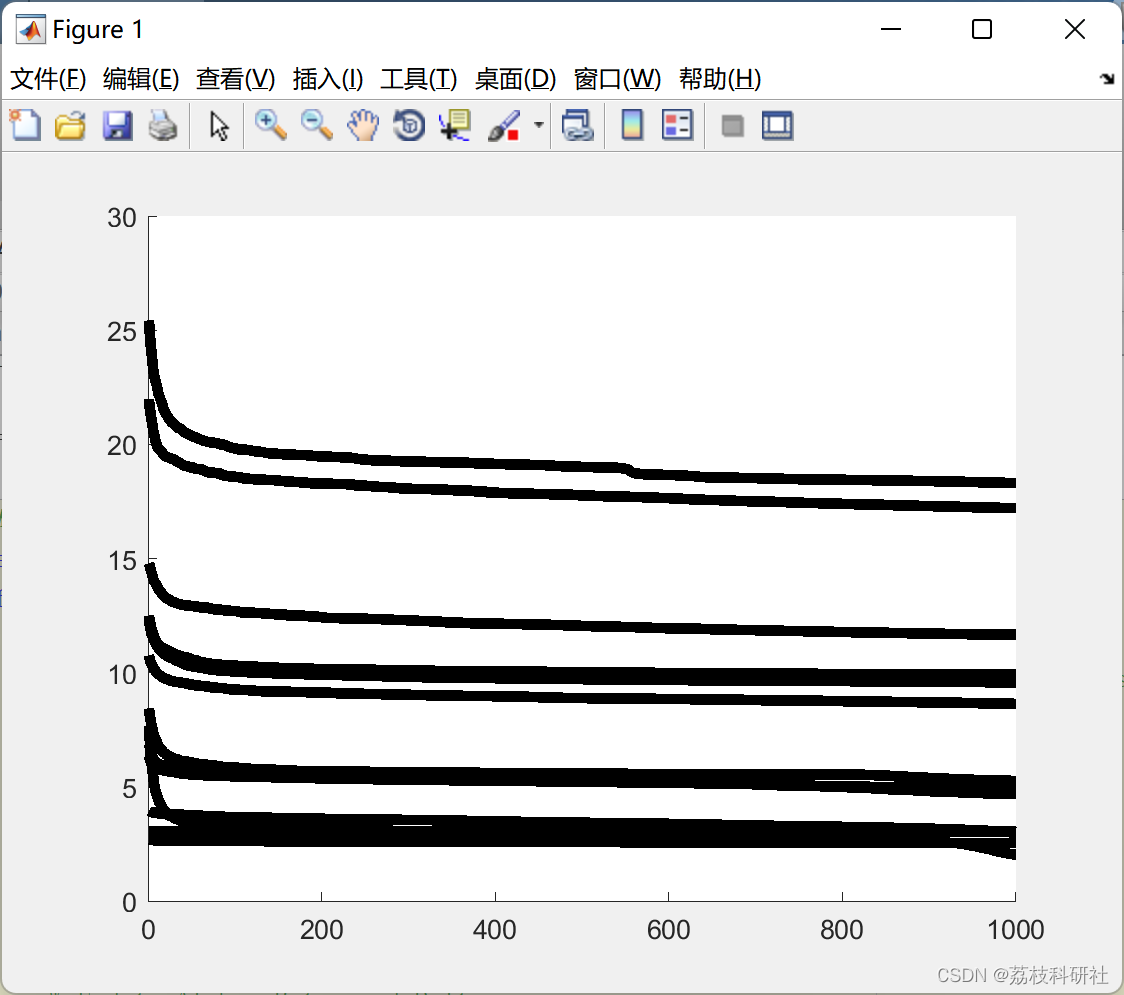
📚2 运行结果

部分代码：

clc
clear

global NFE
NFE=0;

nPop=30;    % Number of search agents (Population Number)
MaxIt=1000; % Maximum number of iterations
nVar=30;    % Number of Optimization Variables

Total_Runs=25;

% Pre-allocating vectors and matrices
Cost_Rsult=nan(1,Total_Runs);
Rsult=nan(Total_Runs,MaxIt);
Mean=nan(1,14);
Best=Mean;
Std=Mean;
nfe=Mean;
fitness1=nan(1,nPop);

for nFun=1:14
    NFE=0;
    CostFunction=@(x,nFun) Cost(x,nFun);        % Cost Function
    for run_no=1:Total_Runs
        
        %% Problem Definition
        
        VarMin=-100;             % Decision Variables Lower Bound
        if nFun==7
            VarMin=-600;             % Decision Variables Lower Bound
        end
        if nFun==8
            VarMin=-32;             % Decision Variables Lower Bound
        end
        if nFun==9
            VarMin=-5;             % Decision Variables Lower Bound
        end
        if nFun==10
            VarMin=-5;             % Decision Variables Lower Bound
        end
        if nFun==11
            VarMin=-0.5;             % Decision Variables Lower Bound
        end
        if nFun==12
            VarMin=-pi;             % Decision Variables Lower Bound
        end
        if nFun==14
            VarMin=-100;             % Decision Variables Lower Bound
        end
        VarMax= -VarMin;             % Decision Variables Upper Bound
        if nFun==13
            VarMin=-3;             % Decision Variables Lower Bound
            VarMax= 1;             % Decision Variables Upper Bound
        end
        
        %%   Grey Wold Optimizer (GWO)

        % Initialize Best Solution (Alpha) which will be used for archiving
        Alpha_pos=zeros(1,nVar);
        Alpha_score=inf;
                
        % Initialize the positions of search agents
        Positions=rand(nPop,nVar).*(VarMax-VarMin)+VarMin;
        Positions1=rand(nPop,nVar).*(VarMax-VarMin)+VarMin;
        BestCosts=zeros(1,MaxIt);

        fitness(1:nPop)=inf;

        iter=0;  % Loop counter
        
        %% Main loop
        while iter<MaxIt
            for i=1:nPop
                
                % Return back the search agents that go beyond the boundaries of the search space
                Flag4ub=Positions1(i,:)>VarMax;
                Flag4lb=Positions1(i,:)<VarMin;
                Positions1(i,:)=(Positions1(i,:).*(~(Flag4ub+Flag4lb)))+VarMax.*Flag4ub+VarMin.*Flag4lb;
                
                % Calculate objective function for each search agent
                fitness1(i)= CostFunction(Positions1(i,:), nFun);
                
                %  Grey Wolves
                if fitness1(i)<fitness(i)
                    Positions(i,:)=Positions1(i,:);
                    fitness(i) =fitness1(i) ;
                end
                
                % Update Best Solution (Alpha) for archiving
                if fitness(i)<Alpha_score
                    Alpha_score=fitness(i);
                    Alpha_pos=Positions(i,:);
                end
                
            end
            
            a=2-(iter*((2)/MaxIt));  % a decreases linearly fron 2 to 0
            
            % Update the Position of all search agents
            for i=1:nPop
                for j=1:nVar
                    
                    GGG=randperm(nPop-1,3);
                    ind1= GGG>=i;
                    GGG(ind1)=GGG(ind1)+1;
                    m1=GGG(1);
                    m2=GGG(2);
                    m3=GGG(3);
                    
                    r1=rand;
                    r2=rand;
                    
                    A1=2*a*r1-a;
                    C1=2*r2;
                    
                    D_alpha=abs(C1*Positions(m1,j)-Positions(i,j));
                    X1=Positions(m1,j)-A1*D_alpha;
                    
                    r1=rand;
                    r2=rand;
                    
                    A2=2*a*r1-a;
                    C2=2*r2;
                    
                    D_beta=abs(C2*Positions(m2,j)-Positions(i,j));
                    X2=Positions(m2,j)-A2*D_beta;
                    
                    r1=rand;
                    r2=rand;
                    
                    A3=2*a*r1-a;
                    C3=2*r2;
                    
                    D_delta=abs(C3*Positions(m3,j)-Positions(i,j));
                    X3=Positions(m3,j)-A3*D_delta;
                    Positions1(i,j)=(X1+X2+X3)/3;
                    
                end
            end
            
            iter=iter+1;
            BestCosts(iter)=Alpha_score;
            
            fprintf('Func No= %-2.0f,  Run No= %-2.0f,  Iter= %g, Best Cost = %g\n',nFun,run_no,iter,Alpha_score);
            
        end

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

Akbari, Ebrahim, et al. “A Greedy Non-Hierarchical Grey Wolf Optimizer for Real-World Optimization.” Electronics Letters, Institution of Engineering and Technology (IET), Apr. 2021, doi:10.1049/ell2.12176.

🌈4 Matlab代码实现